8. De la semicardioidă la cardioidă, simetrizând faţă de axă

În §7 am urmat o idee exotică: am extins prin pathforall conturul semicardioidei superioare, obţinând conturul întregii cardioide (pentru fiecare instrucţiune x y lineto existentă, am adăugat conturului iniţial şi x -y lineto); dar astfel, am putut evidenţia ce este de fapt, un "contur".
Să revenim la calea firească: "întregim" cardioida simetrizând faţă de axa $Ox$ conturul semicardioidei (în loc să-l extindem, cum am făcut în §7).

Întâi avem de subliniat că nu merge o schemă de lucru în care conturul să fie instanţiat o singură dată:

Kardioid  % adaugă conturului curent şi semicardioida superioară K
gsave  stroke  grestore  % trasează conturul curent (K se păstrează)
gsave
     1 -1 scale  % inversează sensul pe axa Oy (vrând semicardioida inferioară)
     stroke  % trasează conturul curent; K nu este inversat!
grestore

stroke trasează conturul curent şi trebuie să se ţină seama de situaţia obişnuită, când acesta conţine şi alte contururi, nu numai pe acela căruia, în prealabil, ai vrea să-i aplici o anumită transformare. Decurge firesc această regulă: după ce se indică transformarea, trebuie precizat cumva şi conturul căruia îi va fi aplicată aceasta; perechea de operatori gsave şi grestore deservesc şi ei, acest principiu de lucru (permiţând comutarea temporară într-un context grafic nou).

Ţinând seama de regula menţionată, programul din §7 se rescrie astfel:

%!PS
% coordonatele punctelor semicardioidei K(t) (t este implicit, în vârful stivei)
/X {2 mul dup 1 sub mul} bind def                    % X(t) = 2t(2t-1)
/Y {dup dup 1 exch sub mul sqrt mul 4 mul} bind def  % Y(t) = 4tSQRT(t(1-t))

/N 1000 def  % /N 4 def
% aproximare poligonală (cu N segmente) a semicardioidei superioare
/Kardioid {
    0 0 moveto  % conturul pleacă din K(0) (vârful cardioidei)
    1 1 N { N div dup X exch Y lineto } for
} bind def

90 90 scale  % 90bp = 72bp + 18bp = 1.25 inch (= 4.175 cm)
1.5 5 translate  % originea figurii: 135bp de marginea stângă, 450bp de jos
.005 setlinewidth  % 0.005 din 90bp

gsave  
    Kardioid  % instanţază (şi trasează) conturul semicardioidei
    stroke
grestore

gsave
    1 -1 scale  % (x,y) --> (x,-y)  (simetrizează faţă de axa Ox curentă)
    Kardioid  % instanţiază (pentru noul xOy), conturul semicardioidei
    1 0 0 setrgbcolor  stroke
grestore

Iterând programul pentru N=4 (caz în care este uşor de văzut conţinutul conturului înainte şi după simetrizare, folosind pathforall cum am arătat în §7) şi N=1000 obţinem:

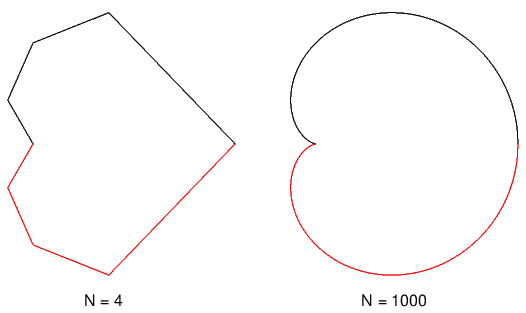
Acum, fiindcă am folosit un acelaşi contur de două ori, putem şi distinge (aici, prin culoare) între cele două semicardioide (spre deosebire de §7, unde întâi am "întregit" conturul şi apoi l-am plotat ca atare, ceea ce exclude posibilitatea marcării separate a părţilor). Să observăm însă că de executat sunt tot 2N+2 instrucţiuni: câte una moveto şi câte N lineto pentru fiecare dintre cele două instanţe ale conturului.