Problemă: să se construiască parabola care conţine un arc de parabolă dat.

Enunţul îndeamnă în mod tacit la o mică reflecţie: ce ar putea însemna "a construi" un obiect (precum parabola) şi respectiv, "a da" un arc de parabolă? Să observăm că dacă înlocuim "parabolă" cu "cerc", problema nu mai prezintă interes (găsim centrul cercului intersectând mediatoarele a două coarde ale arcului).
Vom arăta că parabola este complet determinată dacă se cunosc două puncte ale sale şi (într-un caz) încă un anumit punct, sau (în al doilea caz) anumite două puncte; a da un arc de parabolă echivalează cu a preciza, după caz, o curbă Bézier de gradul 2, respectiv o anumită cubică Bézier; extinderea la întreaga axă a expresiei analitice a acesteia (în primul caz) ne dă chiar parabola din care face parte arcul dat.

Deducerea parabolei dintr-un arc dat al său

Amintim întâi două proprietăţi elementare ale parabolei:
       (i) dreapta care uneşte mijlocul unei coarde cu punctul de intersecţie a tangentelor în capetele acesteia este paralelă cu axa parabolei;
       (ii) dreapta care uneşte un punct al parabolei cu focarul acesteia este simetrică faţă de tangenta în acel punct, cu dreapta care trece prin punctul respectiv şi este paralelă axei parabolei.
Amintim şi definiţia cea mai obişnuită: parabola este locul geometric al punctelor egal depărtate de un punct fix $F$ (focarul) şi de o dreaptă fixă $d$ (directoarea parabolei).

Fie $\mathcal{P}$ un arc de parabolă, de capete $P$ şi $Q$. Fie $M$ mijlocul coardei $PQ$ şi fie $H$ intersecţia tangentelor în capete; după (i), $HM$ este paralelă cu axa parabolei şi ţinând seama de (ii), deducem că simetricele faţă de tangente ale paralelelor la $HM$ duse prin capete se intersectează în focarul $F$ al parabolei:

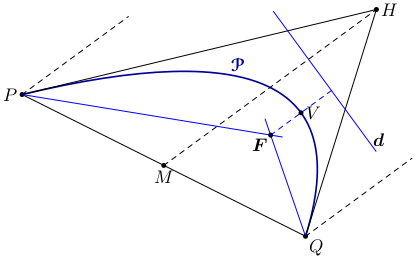
Paralela prin $F$ la $HM$ este chiar axa parabolei, iar intersecţia acesteia cu $\mathcal{P}$ este vârful $V$ al parabolei; dreapta $d$ care trece prin simetricul lui $F$ faţă de $V$ şi este perpendiculară pe axa $VF$ este directoarea parabolei.

Odată ce am găsit focarul şi directoarea, parabola din care face parte arcul dat iniţial este complet determinată (şi implicit, "construită"); să observăm că am avut nevoie doar de aceste trei puncte: capetele arcului şi intersecţia tangentelor în acestea.

Arcele de parabolă sunt curbe Bézier pătratice

Justificarea considerării punctului $H$, de intersecţie a tangentelor în capetele coardei $PQ$ a parabolei, decurge dintr-o metodă generală de construcţie punctuală a unei conice (v. Steiner's generation of a conic), care în cazul nostru revine la această proprietate:
dacă punctele $U$ şi $V$ împart segmentele orientate $\overline{PH}$ şi $\overline{HQ}$ într-un acelaşi raport $t\in[0,1]$, atunci punctul care împarte $\overline{UV}$ în raportul $t$ descrie (când $t$ variază de la 0 la 1) un arc de parabolă, care este tangent dreptelor $PH$ şi $QH$.

Pentru demonstraţie, să considerăm afixele punctelor, notându-le în mod omonim ($P$ are afixul $\mathsf{P}\in\mathbb{C}$, $U$ are afixul $\mathsf{U}\in\mathbb{C}$, etc.). Punctul care împarte $\overline{UV}$ în raportul $t$ este $z(t)=(1-t)\mathsf{U}+t\mathsf{V}$; dar – fiindcă $U$ împarte $\overline{PH}$ în raportul $t$ – avem $\mathsf{U}=(1-t)\mathsf{P}+t\mathsf{H}$; analog, $\mathsf{V}=(1-t)\mathsf{H}+t\mathsf{Q}$. Rezultă: $$z(t)=(1-t)^2\mathsf{P}+2t(1-t)\mathsf{H}+t^2\mathsf{Q},\,t\in[0,1]\quad\quad\quad(1)$$ Deci (plecând de la faptul că sunt date de o funcţie de gradul doi în $t$) punctele $z(t)$ se află pe o parabolă care trece prin $z(0)=\mathsf{P}$ şi $z(1)=\mathsf{Q}$.
Obs. De fapt, nu-i uşor de arătat direct că (1) este într-adevăr, ecuaţia unei parabole…
Din (1) rezultă că $x=x(t)$ şi $y=y(t)$ (partea reală a lui $z(t)$, şi cea imaginară) sunt funcţii de gradul doi în $t$; eliminând cumva parametrul – cum arătăm pe un exemplu, mai jos – rezultă o ecuaţie de gradul doi în $x$ şi $y$, deci ecuaţia unei conice şi rămâne de verificat condiţia necesară ($B^2=4AC$) pentru ca aceasta să fie chiar o parabolă.

Avem $z'(t)=-2(1-t)\mathsf{P}+2(1-2t)\mathsf{H}+2t\mathsf{Q}$; rezultă că $z'(0)=2(\mathsf{H}-\mathsf{P})$ – adică tangenta în $z(0)$ are aceeaşi direcţie ca vectorul $\overline{PH}$ – şi $z'(1)=2(\mathsf{Q}-\mathsf{H})$; deci dreptele $PH$ şi $HQ$ sunt tangente parabolei, în $P$ şi respectiv în $Q$.
De fapt se vede uşor că avem $z'(t)=2(\mathsf{V}-\mathsf{U})$ (nu numai în capetele $P$, $Q$), deci dreaptele $UV$ sunt tangente parabolei respective (se zice că înfăşoară parabola).

Arcul de parabolă $z(t)$ rezultat mai sus este curba Bézier pătratică definită de capetele $P$, $Q$ şi de "punctul de control" $H$.
Obs. Unele fonturi (de exemplu TrueType) prevăd imprimarea contururilor caracterelor prin combinarea de instrucţiuni "lineto" (trasează un segment de capete date) şi de instrucţiuni de trasare a unui arc de parabolă (curbă Bézier pătratică) – fiecare arc de parabolă fiind trasat prin câte o singură instrucţiune, având ca argumente capetele arcului şi un "punct de control".

Să observăm că nu există nicio piedică pentru a considera (1) cu $t\in(-\infty,+\infty)$ (în loc de restrângerea la domeniul curbei Bézier, $t\in[0,1]$) – obţinând astfel "întreaga" parabolă din care face parte arcul dat de (1).

Exerciţiu (determină parabola, ştiind un arc al său)

Fiind date coordonatele punctelor din figura de mai sus

Înlocuind în (1) $\mathsf{P}=1+2i$, $\mathsf{Q}=3+i$ şi $\mathsf{H}=3.5+2.6i$ şi evidenţiind părţile (reală şi imaginară) prin $z(t)=x(t)+iy(t)$ – găsim uşor:

Nu-i necesar, dar dacă vrem, putem elimina $t^2$: avem $2.2x-3y=7.4t-3.8$; de aici, $t=(11x-15y+19)/37$ şi înlocuind în $x(t)$ obţinem ecuaţia carteziană şi o putem aduce (de exemplu cu SymPy, dacă vrem să ne scutim de calculul manual) la forma standard: $121x^2+225y^2-330xy+196x+355y-1267=0$; condiţia ca aceasta să fie ecuaţia unei parabole este $B^2-4AC=0$, unde $A$, $B$ şi $C$ sunt coeficienţii lui $x^2$, $xy$ şi $y^2$ – şi se verifică imediat că este satisfăcută.

Să verificăm că tangenta în $P$ trece prin $H$; avem $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}t}\frac{\mathrm{d}t}{\mathrm{d}x}=\frac{y'(t)}{x'(t)}=\frac{-4.4t+1.2}{-6t+5}$. Avem $x(t)=1$ şi $y(t)=2$ numai dacă $t=0$; deci tangenta în $P(1,2)$ are panta $\frac{y'(0)}{x'(0)}=0.24$ şi ecuaţia tangentei este $y-2=0.24(x-1)$; se vede uşor că este satisfăcută de punctul $H(3.5,2.6)$.
Analog, găsim ecuaţia tangentei în $Q$ (alegând $t=1$; de altfel – ştiam de când am găsit (1), că $z(0)$ şi $z(1)$ corespund capetelor arcului dat): $y-1=3.2(x-3)$ – care este şi ea satisfăcută de punctul $H$.

Să găsim vârful $V$ şi axa parabolei.
Ştim (vezi figura de mai sus) că $HM$ este paralelă cu axa parabolei, unde $M(2,1.5)$ este mijlocul coardei $PQ$; deci axa are panta $m_{HM}=\frac{2.6-1.5}{3.5-2}=\frac{11}{15}$; rezultă că tangenta în $V$ are panta $-1/m_{HM}=-\frac{15}{11}$. Găsim valoarea lui $t$ corespunzătoare acestei pante din $\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{-4.4t+1.2}{-6t+5}=-\frac{15}{11}$, anume $t=\frac{441}{692}$ (şi acum putem calcula coordonatele $x(t)$ şi $y(t)$ ale lui $V$, apoi şi ecuaţia axei parabolei).

Să producem "întreaga" parabolă (pe de o parte, pentru a confrunta cu arcul $\mathcal{P}$ trasat în figura de mai sus), modelând aceste calcule într-un program R:

draw_segment <- function(z2, z1, ...) {  # uneşte punctele de afixe z1, z2
    segments(Re(z1), Im(z1), Re(z2), Im(z2), ...) }
draw_segments <- function(list_2z, ...) {  # trasează segmentele din listă
    for(z in list_2z) draw_segment(z[1], z[2], ...) }

Z <- function(t) {  # z(t) pentru o valoare t, sau pentru o secvenţă de valori t
    xt <- -3*t^2 + 5*t +1
    yt <- -2.2*t^2 + 1.2*t + 2
    xt + 1i*yt
}
t_R <- seq(-0.5, 1.5, by=0.01)  # secvenţă t pentru "întreaga" parabolă
t_01 <- seq(0, 1, by=0.01)  # secvenţă t pentru un arc de parabolă

plot(Z(t_R), asp=1, type="n", bty="n", 
     xlim=c(-1, 3.5), ylim=c(-1, 3.5)) # iniţializează fereastra grafică

points(Z(t_R), type="l", lwd=1)  # trasează "întreaga" parabolă
points(Z(t_01), type="l", lwd=1.5, col="blue")  # "îngroaşă" arcul de parabolă
P = Z(0); Q = Z(1)  # capetele arcului de parabolă
H = 3.5 + 2.6i  # punctul de intersecţie a tangentelor în capete
Up = -0.5*H + 1.5*P; Uq = -0.5*H + 1.5*Q  # puncte mai depărtate, ale tangentelor
V = Z(441/692)  # vârful parabolei
W = 1i*(Im(V)-11/15*Re(V))  # intersecţia axei parabolei cu axa imaginară
points(c(P, Q, H, V), pch=20, cex=0.6)  # marchează punctele
draw_segments(list(c(H, Up), c(H, Uq), c(V, W)), lwd=0.3)  
text(c(P, Q, H, V), labels=c("P", "Q", "H", "V"), pos=c(3, 4, 4, 4), cex=0.9)
grid()

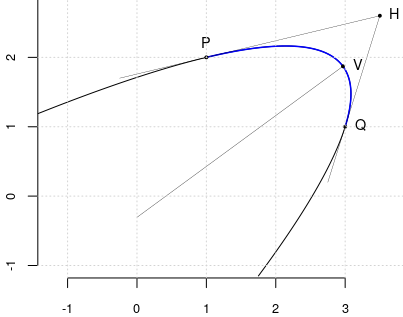
Recunoaştem desigur, arcul $\mathcal{P}$ din prima figură - doar că diferă unitatea de măsură. Dar deosebirea de principiu esenţială, între programul cu care am realizat prima figură (folosind MetaPost) şi programul R tocmai redat este următoarea: pentru a trasa $\mathcal{P}$, în MetaPost am folosit o singură instrucţiune (similară cu instrucţiunea curveto din PostScript, prin care se produce o cubică Bézier), în timp ce în R am folosit o secvenţă de 100 de valori $t\in[0,1]$ şi în memorie s-au constituit efectiv 100 de puncte $z(t)$, care apoi, unite consecutiv prin segmente (adică folosind 100 de instrucţiuni ca lineto din PostScript), au generat arcul $\mathcal{P}$.

Arcele de parabolă, prin cubice Bézier

John Warnock — cu mult timp înainte de a înfiinţa Adobe Systems şi de a şi crea prin 1982, limbajul PostScript — şi Donald Knuth — fondatorul tipografiei digitale, prin sistemul TeX şi limbajul MetaFont, lansate prin 1978 — au avut ideea de a folosi curbele Bézier (cele cubice) pentru a descrie contururile grafice ale caracterelor (curbele Bézier apăruseră prin 1960 – graţie lui Pierre Bézier şi Paul de Casteljau – ca instrument matematic pentru descrierea profilelor specifice industriei automobilelor).

O cubică Bézier are două "puncte de control", permiţând (cu preţul unei anumite creşteri a efortului de calcul) o mai mare varietate de forme grafice, faţă de curbele Bézier pătratice (1) (care, având un singur punct de control, pot genera doar arce de parabolă, cum am arătat mai sus; desigur… putem obţine şi aşa, "o mare varietate de forme" – îmbinând între ele mai multe asemenea arce, suficient de mici).

Având date un punct iniţial $P$ şi unul final $Q$, să vedem cum am găsi două puncte "de control" $F$ şi $G$ care să aibă aceeaşi proprietate ca punctul $H$ de mai sus – în primul rând, $FP$ şi $GQ$ să fie tangente curbei din care face parte arcul trasat între $P$ şi $Q$; deci $F$ şi $G$ trebuie căutate pe dreptele $HP$ şi $HQ$, unde $H$ este ca şi mai sus, intersecţia tangentelor în capetele arcului "dat".

Restrângând pentru început lucrurile, să presupunem că arcul de capete $P$ şi $Q$ este chiar un arc de parabolă, deci poate fi reprezentat prin formula (1); dar acum vrem un polinom de gradul trei, care să "reprezinte" cumva, arcul de parabolă $z(t)$ din (1). Cubica respectivă ar trece prin capetele $P$ şi $Q$ (pentru $t=0$ şi $t=1$) dacă polinomul ar conţine monoamele $(1-t)^3\mathsf{P}$ şi $t^3\mathsf{Q}$, iar celelalte două monoame ar conţine $t(1-t)$ (încât ele să nu afecteze valorile în capetele $t\in\{0,1\}$).

Observând că $(1-t)+t=1$, putem satisface aceste cerinţe înmulţind $z(t)$ cu $(1-t)$ şi respectiv cu $t$ şi adunând apoi rezultatele; rezultă astfel această rescriere:

Punctele de control căutate $F$ şi $G$ ar fi reprezentate de cei doi coeficienţi din mijloc, dar nu direct - fiindcă (de exemplu, pentru primul coeficient) punctul de afix $2\mathsf{H}+\mathsf{P}$ este exterior dreptei $HP$ (originea planului fiind fixată arbitrar).
Pentru ca $F$ să se afle "la momentul" $t$ pe segmentul orientat $\overline{PH}$ şi în acelaşi timp, să se afle pe raza polară a punctului $2\mathsf{H}+\mathsf{P}$ trebuie îndeplinită pentru un anumit factor $\lambda$, condiţia: $(1-t)\mathsf{P}+t\mathsf{H}=\lambda(2\mathsf{H}+\mathsf{P})$ din care deducem $2\lambda=t$ şi $\lambda=1-t$, care adunate, ne dau $\lambda=\frac{1}{3}$. Prin urmare (procedând analog pentru $G$),

Pentru a evita factorul $\frac{1}{3}$, putem amplifica monoamele din mijloc cu $3$, obţinând o expresie mai obişnuită a cubicei Bézier:

asociate capetelor unui arc de curbă date de coeficienţii extremi şi punctelor de control date de coeficienţii din mijloc.

Acum, să observăm că $F$ şi $G$ din polinomul (3) pot să aibă orice valoare, nu neapărat valorile date de (2) – valori pe care le găsisem mai sus presupunând ("pentru început", cum subliniam mai sus) că arcul de capete $P$ şi $Q$ era un arc de parabolă.
Fiindcă $z'(t)=3(1-t)^2(\mathsf{F}-\mathsf{P})+6(1-t)t(\mathsf{G-F})+3t^2(\mathsf{Q-\mathsf{G}})$, rezultă că $PF$ şi $GQ$ sunt tangente arcului de capete $P$ şi $Q$ (chiar şi dacă $F$ şi $G$ nu satisfac (2), adică şi în cazul când arcul dat nu este un arc de parabolă).

Conturul corespunzător cubicei Bézier (3) se obţine considerând "punctul curent" în $P$ şi indicând operatorului PostScript curveto (sau operatorului "path_join" notat cu ".." în MetaFont şi în MetaPost) coordonatele punctelor $F$, $G$ şi $Q$; dacă pentru $F$ şi $G$ folosim formulele (2), atunci rezultă neapărat un arc de parabolă.

Aplicaţie…

Următorul program MetaPost produce direct (fără a implica ecuaţiile parametrice) o figură ca aceea de la început; fiind date punctele $P$, $Q$ şi $H$, se constituie arcul de parabolă de capete $P$ şi $Q$ cu proprietatea că tangentele în capete se taie în $H$, folosind o singură instrucţiune: p0 = P .. controls c1 and c2 .. Q;, în care punctele de control (pentru cubica Bézier modelată de operatorul "..") sunt determinate conform "teoriei" expuse mai sus, c1=$(2\mathsf{H}+\mathsf{P})/3$ şi c2=$(2\mathsf{H}+\mathsf{Q})/3$; apoi programul modelează operaţiile geometrice descrise la început: se calculează unghiul tangentei $HP$ cu axa parabolei (unghi egal cu cel dintre tangentă şi paralela prin $P$ la dreapta $HM$, unde $M$ este mijlocul coardei $PQ$) – şi aşa mai departe, cum se vede în comentariile pe care le-am adăugat pe liniile de program.

Programul este "lung", dar complet; primele 8 linii servesc în orice program MetaPost, când vrem să obţinem în final un document PDF conţinând figurile pe care le descrie programul respectiv; vreo 10 linii din program deservesc etichetarea figurii.

prologues:=3;  % asigură înglobarea fonturilor în PDF
verbatimtex  % pentru LaTex, când va fi invocat pentru a produce etichetele
    \documentclass[11pt]{article}
    \usepackage{lmodern}
    \usepackage{amssymb,amsmath}
    \usepackage [mathscr]{euscript}  % vom nota arcul cu un "glyph" caligrafic  
    \begin{document}
etex

vardef acosd primary x = angle (x, 1 +-+ x) enddef;  % unghiul de cosinus dat

u = 3cm;  % unitatea de măsură (pentru operaţiile 'scale')
pair P, Q, H, M, F, V;  % declară punctele de lucru

P = (1, 2); Q = (3, 1);  % capetele arcului de parabolă "dat"
H = (3.5, 2.6);  % intersecţia tangentelor în capete

beginfig(1);
    path p[]; pair c[];  % contururi 'p0', 'p1', etc. şi puncte 'c1', 'c2' etc.
    c1 = (1/3)*(2*H + P);  % (2H + P)/3  
    c2 = (1/3)*(2*H + Q);  % (2H + Q)/3  (punctele de control ale cubicei Bézier)
    p0 = P .. controls c1 and c2 .. Q;  % P moveto c1 c2 Q curveto  (PostScript) 
    draw p0 scaled u withpen pencircle scaled 1 withcolor .6blue;
    drawoptions(withpen pencircle scaled 0.1);  % celelalte linii vor fi subţiri
    draw (P -- H -- Q -- cycle) scaled u;
    dotlabel.lft(btex $P$ etex, P scaled u);  % etichetează (prin TeX) punctele
    dotlabel.lrt(btex $Q$ etex, Q scaled u);
    dotlabel.rt(btex $H$ etex, H scaled u);
    M = .5[P, Q];  % mijlocul coardei PQ
    dotlabel.bot(btex $M$ etex, M scaled u);
    p1 = M -- .5[H, M];
    p2 = p1 shifted (P-M);  % paralela prin P la axa parabolei (fie aici, 'Px')
    c3 = point 1 of p2;  % acum află unghiul tangentei HP cu axa parabolei:
    gp = acosd (((c3-P) dotprod (H-P)) / (abs(c3-P)*abs(H-P)));
    c4 = c3 rotatedaround(P, -2*gp);  % simetrizează 'Px' faţă de tangenta prin P
    p4 = P -- 2[P, c4];  % dreapta prin P care trece prin focarul F
    draw p4 scaled u  withcolor blue;  % trasează 'Px'
    p3 = p1 shifted (Q-M);  % paralela prin Q la axa parabolei (fie aici, 'Qx')
    c5 = point 1 of p3;
    gq = acosd (((c5-Q) dotprod (H-Q)) / (abs(c5-Q)*abs(H-Q)));
    c6 = c5 rotatedaround(Q, 2*gq);  % simetrizează 'Qx' faţă de tangenta prin Q
    p5 = Q -- .94[Q,c6];  % dreapta prin Q care trece prin focarul F
    draw p5 scaled u  withcolor blue;
    F = p5 intersectionpoint p4;  % PF intersectat cu QF
    dotlabel.llft(btex $\boldsymbol{F}$ etex, F scaled u);
    p6 = p1 shifted (F-M);
    draw (M -- H) scaled u  dashed evenly;
    draw p2 scaled u  dashed evenly;
    draw p3 scaled u  dashed evenly;
    V = p0 intersectionpoint p6;  % vârful parabolei
    dotlabel.rt(btex ${V}$ etex, V scaled u);
    draw (F -- V) scaled u  dashed evenly withcolor blue;
    c7 + F = 2V;  % punctul 'c7' aparţine directoarei parabolei
    c8 = F rotatedaround(c7, 90);
    draw (c7 -- V) scaled u  dashed evenly withcolor blue; 
    draw (c8 -- 2.3[c8,c7]) scaled u  withcolor blue;
    label.top(btex $\boldsymbol{d}$ etex, (c8 shifted (0.02,0)) scaled u);
    label.top(btex $\boldsymbol{\mathscr{P}}$ etex, 
              (point 0.4 of p0) scaled u) withcolor .6blue;
endfig;
end

Compilăm programul prin mpost -tex=latex arcparab.mp; astfel (cu opţiunea "-tex=latex"), producerea etichetelor notate între btex şi etex va fi pasată automat compilatorului de LaTeX (furnizându-i preambulul precizat în verbatimtex). Rezultă fişierul în format EPS "arcparab.1" (corespunzător figurii descrise în program sub beginfig(1)); apoi folosim ps2pdf arcparab.1, pentru a transforma în document PDF (şi putem folosi Ghostscript cum am arătat în [1], pentru a seta în fişierul PDF respectiv, câmpul "/CropBox" – restrângând pagina produsă, la cadrul figurii; ulterior, figura respectivă poate fi încorporată ca atare, într-un document LaTeX oarecare). Fişierul PDF rezultat măsoară cam de trei ori mai puţin decât fişierul EPS iniţial, sau faţă de o copie-ecran a figurii (decupată din fereastra unui "Document Viewer" în care vom fi deschis pe ecran fişierul PDF).