Calculul coeficienţilor binomiali
Am improvizat la clasă acest exerciţiu: să se scrie într-un fişier toţi termenii unei dezvoltări binomiale (a + b)n; care este cel mai mare termen, pentru a = 1/4, b = 5/4 şi n = 2008?
Aveam în vedere că tocmai se parcursese capitolul de "analiză combinatorică" (la Matematică) şi iniţial nu vizam nimic special - doar tematica didactică obişnuită: angajează o funcţie pentru calculul coeficienţilor binomiali, una pentru maximul tabloului, etc. ("utilizarea subprogramelor").
Dar la Matematică aceşti C(n, k) sunt utilizaţi formal (operând cu expresii, nu cu valori), pe când într-un program ei sunt efectiv nişte numere şi apar veşnicele probleme de reprezentare şi de calcul, angajând un limbaj sau altul.
Cel mai mare termen al dezvoltării
Tratăm întâi această chestiune, dat fiind că pentru a găsi cel mai mare termen al dezvoltării nu este necesar să calculăm termenii: este suficient să calculăm rapoartele de termeni consecutivi T(k+2) / T(k+1) = b/a * (n-k)/(k+1) (a vedea vreun manual "Matematică", cl. a X-a) - cu avantajul esenţial că astfel putem evita erorile "overflow" şi valorile "inf" de care va fi vorba mai jos.
Următorul program este ingenios: imită raţionamentul pus în manualul de Matematică pentru diverse exerciţii de acest tip (se compară raportul menţionat cu 1, căutând punctul k în care se schimbă monotonia):
#include <iostream> #include <cstdlib> // std::atof(), std::atoi() using namespace std; inline int sgn(double x) { // Semnul numărului return (x > 0 ? 1 : (x < 0 ? -1 : 0)); } int main(int argc, char* argv[]) { double a = atof(argv[1]), b = atof(argv[2]); int n = atoi(argv[3]), k; // Diferenţele faţă de 1 ale rapoartelor de termeni consecutivi double * dif1 = new double[n]; for(k = 0; k < n; k++) dif1[k] = b/a*(n-k)/(k+1) - 1; int s = sgn(dif1[0]); k = 1; while(k < n && sgn(dif1[k]) == s) k++; cout << "Rangul termenului maxim: " << (k+1) << '\n'; }
vb@vb:~$ g++ -o rang-max rang-termen-max.cpp vb@vb:~$ ./rang-max 0.25 1.25 2008 Rangul termenului maxim: 1675
Am vizat rangul termenului maxim (nu însăşi valoarea acestuia); la Matematică este suficient, fiindcă de regulă răspunsul aşteptat este expresia T1675 şi nu valoarea ei.
"Ingeniozitatea" este însă inutilă: un calcul direct ne dă numărătorul diferenţei dintre raportul menţionat mai sus şi 1, anume -k(a+b) + bn - a şi vedem imediat că punctul de maxim (contextul problemei impune a > 0, b > 0) este (bn - a)/(a + b). Prin urmare, n-aveam nevoie să calculăm toate rapoartele; putem exclude tabloul "dif1" şi funcţia "sgn", reducând programul la unul banal:
#include <math.h> // ceil() int main() { double a, b; int n; cin >> a >> b >> n; cout << "rangul termenului maxim: "; cout << (ceil((b*n - a) / (a + b)) + 1); }
Surprinzător, "Probleme rezolvate" din manualul de Matematică nu sesizează această simplificare şi procedează în fiecare caz la calculul rapoartelor şi studiul monotoniei (de fapt, nu-i "surprinzător" ci chiar aşa trebuie: să mai gândească şi cel care urmăreşte rezolvarea expusă!).
Memoizarea funcţiilor
Pentru calculul coeficienţilor binomiali C(n, k) = 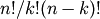 să folosim întâi formularea cea mai simplă, bazată pe recurenţa C(n, k) = C(n-1, k) + C(n-1, k-1). Implementarea mot-à-mot a acestei formule este într-adevăr, ineficientă (se va repeta frecvent calculul aceloraşi termeni) - ceea ce este evidenţiat în orice manual pe cazul similar al şirului lui Fibonacci.
să folosim întâi formularea cea mai simplă, bazată pe recurenţa C(n, k) = C(n-1, k) + C(n-1, k-1). Implementarea mot-à-mot a acestei formule este într-adevăr, ineficientă (se va repeta frecvent calculul aceloraşi termeni) - ceea ce este evidenţiat în orice manual pe cazul similar al şirului lui Fibonacci.
Dar funcţia respectivă poate să fie "eficientizată" angajând un tablou static K[][] pentru a păstra coeficienţii deja calculaţi: la fiecare reapelare C(n, k) se testează întâi K[n][k], returnând direct această valoare dacă ea nu este zero - iar dacă este zero, atunci se continuă reapelarea şi odată determinat, coeficientul respectiv este salvat în K[][] şi returnat.
OBS. O idee similară se utilizează în aplicaţiile Web: paginile generate dinamic de către web-server sunt salvate în cache şi deservirea unui URL decurge astfel: dacă pagina corespunzătoare există în cache, atunci este redată direct versiunea memorată aici; altfel - se cere web-serverului pagina respectivă şi răspunsul este memorat în cache în vederea unei reutilizări directe ulterioare.
Această tehnică de "eficientizare" a algoritmilor recursivi este cunoscută sub numele de memoizare - a vedea memoization, sau "Introducere în algoritmi" (Cormen, Leiserson, Rivest), Ed. Computer Libris Agora, 2000 (pag. 268).
În C++ (la nivelul manualului) putem memoiza gestionând în cadrul funcţiei un tablou static (vom reveni mai jos); dar în Perl există modulul Memoize, iar în Python există un mecanism de "decorare" - permiţând ca o funcţie (scrisă obişnuit, fără variabile sau cod pentru memoizare) să fie completată automat (în momentul compilării ei) cu codul necesar memoizării.
Calculul recursiv, în perl
Memoize::memoize() primeşte ca argument numele funcţiei de memoizat şi confecţionează o nouă funcţie care menţine o zonă de memorie "cache" (înregistrând argumentele curente ale funcţiei primite, împreună cu valoarea calculată pentru acestea); dacă noua funcţie găseşte argumentele în "cache", ea returnează valoarea găsită - altfel, ea apelează funcţia originală, salvează în "cache" valoarea returnată de aceasta şi i-o returnează:
#!/usr/bin/perl -w use Memoize; memoize('comb'); sub comb { # C(n, k) my $n = shift; my $k = shift; return $n if $k == 1; return 1 if $k == $n; comb($n-1, $k-1) + comb($n-1, $k); } print "C(28, 14) = ", comb(28, 14);
Executând programul de mai sus folosind time, iar apoi executându-l după ce am comentat primele două linii - avem respectiv rezultatele următoare:
vb@vb:~$ time ./memo.pl C(28, 14) = 40116600 real 0m0.032s vb@vb:~$ time ./memo.pl # acum fără modulul Memoize C(28, 14) = 40116600 real 0m48.166s
Puteam executa ambele variante - şi cu şi fără memoizare - în acelaşi program (în loc de a repeta execuţia, după comentarea liniilor menţionate) intercalând Memoize::unmemoize('comb'); însă în acest caz ar fi trebuit să suplimentăm cu un cod pentru determinarea timpului de execuţie (de genul $start = time(); $coef = comb(28, 14); $end = time(); print $coef, $end - $start;).
Timpii obţinuţi (sub o secundă, faţă de 48 secunde) arată că folosind memoizarea putem anula "ineficienţa" datorată recalculării de termeni, specifică funcţiilor recursive de genul celeia de mai sus. Putem avea însă un alt aspect de ineficienţă, datorat depăşirii stivei:
vb@vb:~$ time ./memo.pl # cu Memoize, dar pentru C(1000, 500) Deep recursion on anonymous subroutine at ./memo.pl line 10. C(1000, 500) = 2.70288240945436e+299 real 0m4.840s
C(1000, 500) este într-adevăr un număr care are 300 de cifre zecimale, începând cu cele redate - dar "deep recursion" avertizează că de-acum depăşirea stivei este iminentă. Ar putea fi de remarcat faptul că valoarea a fost redată în "format ştiinţific", ceea ce chiar este potrivit: coeficientul respectiv ne trebuie eventual pentru un alt calcul (de exemplu, un termen al unei dezvoltări binomiale) şi nu ca să-i contemplăm cele 300 de cifre zecimale.
Calculul recursiv, în Python
În Python se poate evita repetarea unei aceleiaşi secvenţe de cod (cum ar fi codul necesar memoizării) în cadrul diverselor funcţii proprii, invocând prin operatorul special @ un "decorator" constituit în prealabil (o funcţie, sau o clasă care "internalizează" funcţia asupra căreia se aplică şi care cuprinde secvenţa de cod cu care ar trebui "completată" funcţia respectivă):
#!/usr/bin/python # -*- coding: utf-8 -*- class Memoize: # "decorează" o funcţie cu codul de memoizare def __init__(self, function): self.fn = function self.cache = {} def __call__(self, *args): if not self.cache.has_key(args): self.cache[args] = self.fn(*args) return self.cache[args] @Memoize # ambalează funcţia următoare într-un obiect Memoize def comb(n, k): if k == 1: return n if n == k: return 1 return comb(n-1, k-1) + comb(n-1, k) print "C(142, 71) = ", comb(142, 71)
"Directiva" @Memoize va executa constructorul __init__() al clasei Memoize, luând ca argument referinţa la obiectul definit prin def comb(n, k); obiectul rezultat astfel conţine ca membri fn ("pointer" la comb()) şi dicţionarul cache, iar metoda specială __call()__ va fi apelată totdeauna când este invocată comb(argumente).
vb@vb:~$ time ./memoize.py C(142, 71) = 372641034574519600278163693967644731577200 real 0m0.072s user 0m0.048s sys 0m0.020s
Timpul de execuţie încă se îmbunătăţeşte puţin, dacă adăugăm după cele două "if"-ri şi pe acesta (prin care evităm reapelarea C(n, k) atunci când în "cache" există valoarea C(n, n-k)):
if 2*k > n: return comb(n, n - k)
dar pentru comb(144, 72) obţinem deja RuntimeError: maximum recursion depth exceeded; cu alte cuvinte, s-a depăşit limita fixată pentru numărul de apeluri recursive.
Obs. Dacă am fi rulat programul dintr-un mediu IDE (cum se face în şcoli cu programele C++, punându-le în execuţie din meniul lui MinGW) şi nu direct din linia de comandă - atunci depăşirea stivei se producea şi mai devreme, având în vedere că şi mediul IDE şi programul de executat partajează aceleaşi resurse.
"Maximum recursion depth" este setată implicit la 1000:
vb@vb:~$ python >>> import sys >>> sys.getrecursionlimit() 1000
Dacă este cazul putem mări această valoare, incluzând la începutul programului secvenţa:
import sys sys.setrecursionlimit(1500)
şi atunci devine posibil calculul de exemplu, pentru C(200, 100):
vb@vb:~$ time ./memoize.py C(200, 100) = 90548514656103281165404177077484163874504589675413336841320 real 0m0.072s
Bineînţeles că tot mărind parametrii se ajunge inevitabil la depăşirea stivei de execuţie şi în principiu, calculul coeficienţilor binomiali printr-o funcţie recursivă este impracticabil, în majoritatea limbajelor. Iar Perl, Python în care am experimentat mai sus - sunt totuşi limbaje interpretoare, caz în care stiva de execuţie este partajată între interpretor şi programul propriu; lucrurile pot sta altfel, folosind un compilator (sau limbaj de asamblare).
Câte cifre are C(2008, 1004)?
Vom vedea mai jos, cum stau lucrurile şi pentru C++. Exerciţiul enunţat la început va putea fi tratat ca atare dacă vom putea calcula coeficientul binomial cel mai mare, deci C(2008, 1004) (ceea ce nu ne-a reuşit mai sus, în Perl sau Python).
Folosind scipy putem determina C(2008, 1004):
vb@vb:~$ python >>> from scipy import comb >>> print comb(200, 100) 9.05485146561e+58 >>> print comb(2008, 1004) Warning: overflow encountered in exp inf >>>
Am lansat Python şi am importat funcţia comb() din modulul scipy, testând pentru C(200, 100) (a confrunta cu rezultatul obţinut mai sus prin memoize.py); dar C(2008, 1004) este infinit - depăşeşte limita maximă prevăzută pentru floating point.
Însă comb() - ca şi alte funcţii din scipy - permite şi un parametru suplimentar datorită căruia valoarea este returnată ca "număr natural lung":
>>> comb(2008, 1004, exact=True) 5232815589855133170662184530623381777067749552519938346590499366664088349940654 7812002586028425131345324694210523364847390562520967644075439265702081069631546 4887699809420911058120655023366092247361418396361092923219777082512803940929886 3621007796691619537025882827418267330694184133494914045977019043599587152726425 0308819274449213857734707406167068356365869118158953966384536647294852889937757 3804812582153519420774853307127267492351073868910548057822025743550499345380942 2163524680019043927835759850156188995660313111164809727588259279780938901196657 68881188072551309581027742521356956404424980598400L
Vedem astfel că C(2008, 1004) are peste 600 de cifre zecimale şi rămâne să vedem limita maximă admisă pentru valorile de tip double şi respectiv, long double:
#include <iostream> #include <limits> using namespace std; int main() { cout << "double: " << numeric_limits<double>::max(); cout << '\n'; cout<< "long double: " << numeric_limits<long double>::max(); }
vb@vb:~$ g++ -o limite limite.cpp vb@vb:~$ ./limite double: 1.79769e+308 long double: 1.18973e+4932
Deci double poate reprezenta numere de până la 309-310 cifre zecimale, iar long double - până la 4933 cifre (ceea ce convine evident cazului nostru).
Calculul recursiv, în C++
În programul următor modelăm calculul coeficienţilor binomiali prin formula de recurenţă vizată şi mai înainte, exploatând desigur ideea memoizării:
#include <iostream> using namespace std; long double comb(int n, int k) { long double t1, t2; static long double cache[2010][2010]; if(k == 1) return (long double)n; if(n == k) return (long double)1; t1 = cache[n-1][k-1]; if(!t1) t1 = cache[n-1][k-1] = comb(n-1, k-1); t2 = cache[n-1][k]; if(!t2) t2 = cache[n-1][k] = comb(n-1, k); return t1 + t2; } int main() { int n, k; cin >> n >> k; cout << "C(n, k) = " << comb(n,k); }
Cu această funcţie comb() - am putea acum, să completăm exerciţiul improvizat la început (determinarea tuturor termenilor unei dezvoltări binomiale):
vb@vb:~$ g++ -o qcomb qcomb.cpp vb@vb:~$ ./qcomb 2008 1004 C(n, k) = 5.23282e+602
Desigur, puteam calcula coeficienţii şi direct modelând C(n, k) drept produsul valorilor (n-k+j)/j pentru j = 1..k (ceea ce rezultă uşor după simplificări de factoriale), având grijă să folosim numai valori de tip long double (altfel ajungem iarăşi la valori infinite); dar (şi) din cele de mai sus vedem că nu este cazul să ne ferim de a folosi formulările recursive (blamate cam excesiv, în manuale).
vezi Cărţile mele (de programare)