Experimente cu puncte şi pixeli
În finalul lui [1] schiţasem în câteva linii, un experiment prin care transformam un grup de câmpuri ale unei table de şah citite dintr-un fişier PNG - lăsând impresia că ar fi uşor de obţinut transformata printr-o funcţie complexă a unei imagini (eludând cunoştinţe mai precise despre "imagine", "fişiere PNG", sau pachete specializate); el "ţine" probabil doar într-o anumită măsură, în schimb… generează alte experimente.
1. Citirea imaginii
Este esenţială, înţelegerea prealabilă a reprezentării în memorie a unei imagini:
> require("png") # readPNG() şi writePNG() > img <- readPNG("men32.png", info=TRUE) > class(img); typeof(img) [1] "array" [1] "double" > str(img) num [1:32, 1:384, 1:4] 0 0 0 0 0 0 0 0 0 0 ... # Height × Width × Channels - attr(*, "info")=Dotted pair list of 3 ..$ dim : int [1:2] 384 32 # Width, Height ..$ bit.depth : int 8 ..$ color.type: chr "RGBA" # 4 "canale": Red, Green, Blue, Alpha > img[27, 8:10, 1:4] # la ordonata 27 (de sus în jos), între abscisele 8 şi 10 [,1] [,2] [,3] [,4] [1,] 0.0000000 0.0000000 0.0000000 0.8431373 [2,] 0.6196078 0.6196078 0.6196078 1.0000000 # "#9E9E9EFF" [3,] 1.0000000 1.0000000 1.0000000 0.9764706 > rgb(0.6196078, 0.6196078, 0.6196078, 1.0000000) [1] "#9E9E9EFF"
png::readPNG() a creat obiectul "img" de clasă "array" - în fond, un vector numeric (cu valori de tip "double") cu atributul "dim" şi cu adaptare corespunzătoare a operatorului de indexare "["; după decompresarea secţiunii de date a fişierului, numerele întregi conţinute (reprezentând culoarea fiecărui pixel) au fost scalate la intervalul [0, 1] şi înregistrate apoi în tabloul "img", în ordinea obişnuită de tipărire: de sus în jos şi de la stânga spre dreapta.
dim(img) returnează dimensiunile matricei asociate fiecăruia dintre canale, în ordinea obişnuită "Width", "Height"; dar tabloul tridimensional "img" păstrează valorile în ordinea "Height" (distanţa de la marginea superioară), "Width" (distanţa de la marginea stângă), "Channels" (cu maximum 4 valori - pentru R, G, B, respectiv pentru "canalul alpha").
În exemplul redat mai sus, valorile din img[27, 9, 1:4] constituie împreună culoarea notată prin "#9E9E9EFF" (cum găsim aplicând funcţia rgb()) - deci R, G şi B au acelaşi nivel #9E, iar pixelul respectiv (de abscisă 9, pe a 27-a linie de sus) are setat nivelul de transparenţă maxim, #FF.
Funcţia as.raster() aplică rgb() aşa cum am exemplificat mai sus, returnând o matrice în care pentru fiecare index "Height" × "Width" este înregistrată culoarea pixelului respectiv, în notaţie hexazecimală (cu 3 sau cu 4 octeţi):
> raster <- as.raster(img) > str(raster) 'raster' chr [1:32, 1:384] "#00000000" "#00000000" "#00000000" ... > raster[27, 9] # mai sus, img[27, 9, 1:4] [,1] # regăsim valoarea obţinută aplicând direct rgb() mai sus [1,] "#9E9E9EFF" > plot(raster)
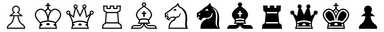
plot(), primind ca argument un obiect de tip "raster", apelează până la urmă rasterImage() - iar aceasta produce pe dispozitivul grafic curent (ecran sau fişier PNG) imaginea reprezentată de "raster"-ul respectiv (redată mai sus, în cazul nostru; în §3 dăm şi alte exemple).
Trebuie să precizăm că există unele excepţii faţă de cele descrise mai sus; de exemplu:
> img <- readPNG("men32_.png") > dim(img) [1] 32 384 2 > raster <- as.raster(img) Error in array(if (d[3L] == 3L) rgb(t(x[, , 1L]), t(x[, , 2L]), t(x[, : a raster array must have exactly 3 or 4 planes
Pentru astfel de cazuri, putem folosi în prealabil programul utilitar convert, pentru a modifica formatul PNG al fişierului:
vb@Home:~/2_art$ convert men32_.png -type TrueColorMatte men32.png
O altă excepţie notabilă vizează (ca de obicei) sistemul Windows (pe care apar probleme legate de "canalul alpha"; a vedea documentaţia pachetului R "png"); dar aici vom neglija cazul când s-ar lucra sub Windows.
2. Puncte, pixeli şi transformări
Sintetizăm lucrurile într-o funcţie prin care se constituie pe deasupra imaginii o reţea de puncte (raportată fie la colţul stânga-jos, fie la centru) şi i se aplică pe rând funcţiile indicate într-un parametru de tip "listă", plotând în câte un panou rezultatul fiecărei transformări:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | konvert <- function(file_png, fun_list=NULL, filename=NULL, ...) { pixels <- png::readPNG(file_png) dimg <- dim(pixels) x <- 1:dimg[2] y <- dimg[1]:1 # ordonatele pixelilor cresc de sus în jos (deci inversăm) center <- (dimg[2] + 1i*dimg[1])/2 # afixul centrului (dar poate fi convenit!) mesh <- outer(x, y, function(u, v) u + 1i*v) # reţea de puncte pe deasupra imaginii tsvet <- as.raster(pixels) # culorile RGB ale "punctelor" FUN <- list(function(u) u) # lista funcţiilor de aplicat reţelei de puncte if(!is.null(fun_list)) { if(!is.list(fun_list)) stop("need a _list_ of functions") FUN <- append(FUN, fun_list) } if(!is.null(filename)) png = png(filename = paste0(filename, ".png"), ...) panels <- length(FUN) # câte un panou grafic pentru fiecare transformare rows <- ceiling(panels/2) opar <- par(mfrow = c(rows, 2), mar=c(0.5, 0, 1, 0), bty="n", xaxt="n", yaxt="n") for(fun in FUN) { text <- deparse(substitute(fun)) # pentru titlul panoului mesh1 <- if(length(formals(fun)) == 1) fun(mesh) else fun(mesh - center) # translatează faţă de centrul convenit plot(mesh1, type="n", asp=1) # stabileşte limitele axelor, pentru a plota punctele points(mesh1, col=tsvet, cex=0.2, pch=19) title(main=paste(sub("function |.Primitive", "", text[1]), "-> ", ifelse(!is.na(text[2]), text[2], text[1])), cex.main=1.5) } par(opar) if(!is.null(filename)) dev.off() } |
Reţeaua de puncte instituită în linia 7 este raportată la sistemul de axe constituit de marginea de jos a imaginii (ca axă reală) şi de marginea stângă (ca axă imaginară). În linia 8, folosind funcţia as.raster() obţinem valorile "R, G, B" ale pixelilor - în ideea de a le folosi ulterior (v. linia 24) drept parametru de culoare, la plotarea transformatei imaginii.
Iar lucrurile par "în regulă": vom deplasa punctele (printr-o funcţie sau alta) - dar indecşii lor în cadrul reţelei de puncte nu se schimbă, deci transformatele vor avea aceleaşi valori "R, G, B" ca şi punctele iniţiale (şi am avea "gratis" această situaţie, fără alte prelucrări); într-adevăr, în linia 7 se pune mesh[x, y] = x + i y, iar apoi în linia 21 sau 22 se schimbă valoarea la aceleaşi coordonate de pixel (din linia 7): mesh1[x, y] = fun(mesh[x, y]) = fun(x + i y).
În linia 9 se constituie o listă conţinând doar funcţia identică; dacă este cazul, în liniile 10-13 această listă este extinsă cu lista de funcţii de transformare care este specificată în parametrul 'fun_list'. În liniile 19-27 se aplică reţelei de puncte câte una dintre aceste transformări şi se expune imaginea rezultată (în primul panou grafic având imaginea iniţială, corespunzător aplicării funcţiei identice). Argumentul '...' (v. linia 1) serveşte pentru a transfera parametri funcţiei png() (v. linia 15), în cazul când s-ar dori salvarea panourilor grafice într-un fişier PNG.
Ilustrăm exploatarea funcţiei concepute mai sus prin următoarea secvenţă (dar în prealabil, am modificat în linia 18 setarea parametrului 'mfrow', încât să obţinem un rând cu patru panouri, în loc de două rânduri cu două coloane):
konvert("chessmen9.png", list(function(u) u^2, sqrt, function(u) sqrt(u)), filena="kvmen", width=894, height=280, units="px", bg="transparent")

Pentru cazul când am vrea să transformăm imaginea nu în raport cu axele implicite (marginea inferioară şi cea stângă), ci în raport cu axele (paralele marginilor) care trec prin centru - am impus în mod tacit convenţia de a preciza un al doilea parametru (iniţializat arbitrar), în definiţia funcţiei: în linia 21 se testează apelând formals(), dacă funcţia respectivă are un singur argument - şi în caz contrar, în linia 22 se translatează reţeaua de puncte iniţială, mutând originea în centrul imaginii (iar "centrul" poate fi eventual modificat, în linia 6).
Astfel, al doilea element al listei de funcţii redate mai sus specifică funcţia nativă "sqrt", cu zero parametri; deci transformarea redată în al treilea panou este raportată la sistemul de axe cu originea în centrul tablei. Dacă am fi vrut "pătratul" imaginii faţă de centru (nu faţă de sistemul de axe implicit, ca în al doilea panou) - adăugam în lista de funcţii "function(u, C=1) u^2" (cu un al doilea parametru); am evitat aceasta, fiindcă imaginea rezultată este dezagreabilă (apar suprapuneri de piese).
Un ultim aspect de menţionat vizează titlurile panourilor. În linia 20 am obţinut "textul" funcţiei, apelând deparse() şi substitute(); de exemplu, '"function (u, ct = TRUE) " "u^2"' (cu două părţi), sau '".Primitive(\"sqrt\")"' (cu un singur element); în linia 25, am folosit sub() pentru a exclude cuvintele iniţiale din prima componentă a textului funcţiei şi am adăugat folosind paste() fie a doua parte a textului dacă există, fie prima parte (în cazul funcţiilor "native", la care "a doua parte" lipseşte).
Acum, numai pentru a ne încredinţa în cazul altor categorii de imagini:

Dar trebuie să precizăm că pentru funcţii de transformare ca exp() sau cos() obţinem imagini inconsistente, sau incoerente…
3. Alte experimente
Să observăm că de fapt, nu imaginea este transformată, ci reţeaua de puncte instituită artificial pe deasupra ei: funcţia de transformare se aplică (în linia 21 sau 22) reţelei de puncte (a cărei definire nu angajează decât caracteristici exterioare ale imaginii), iar imaginea ca atare este implicată doar la plotarea transformatei reţelei (folosind culorile din "raster"-ul asociat imaginii).
Ne-am putea gândi să transformăm cumva şi raster-ul asociat imaginii (nu numai reţeaua de puncte), sau - renunţând la reţeaua de puncte - să "transformăm" şi să plotăm apoi, un obiect de tip "raster" (asociat sau nu, unei imagini existente).
Exemplificăm reluând ideea decoraţiunilor hiperbolice din [1]. Constituim un "raster" angajând diferenţe de pătrate şi îl plotăm:
W <- 300 # width, height x <- y <- 1:W G <- W / 2 # scalăm diferenţele x^2-y^2 pe intervalul [0, 1] raster <- as.raster(outer(x, y, function(u, v) ((u - G)^2 - (v - G)^2) / W^2 + 0.4)) plot(raster)

Funcţia t -> (t - G) / W (unde G = W/2) aplică [0, W] pe [-0.5, 0.5] deci pătratul ei aplică [0, W] pe [0, 0.25]; rezultă că diferenţa pătratelor ei în două puncte oarecare de pe [0, W] este cuprinsă între -0.25 şi 0.25 - încât, adunând cel puţin 0.25 (dar cel mult 0.75) ajungem la valori între 0 şi 1 (aşa cum cere în mod implicit as.raster()). Am obţinut un "gradient hiperbolic": culoarea degradează dinspre marginile laterale spre centru, după şablonul de hiperbolă echilateră.
Putem proceda mai interesant, folosind faptul că as.raster() prevede parametrul "max" - pentru a construi obiecte "raster" cu valori întregi (şi nu între 0 şi 1, ca în cazul implicit max=1):
raster <- as.raster(outer(x, y, function(u, v) ((u - G)^2 - (v - G)^2) %% 256), max=255) plot(raster)
Valorile obţinute (modulând diferenţele de pătrate faţă de 256 şi fixând max=255 - dar putem încerca şi alte valori), sunt interpretate de as.raster() ca nuanţe de gri; reluînd secvenţa de mai sus, pentru "W" 300 şi apoi 600, obţinem aceste "decoraţiuni hiperbolice":


Luând "W" mic, putem observa direct matricea din care provine raster-ul:
> outer(1:10, 1:10, function(u, v) ((u - 5)^2 - (v - 5)^2) %% 300) # sau %100, etc. [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [1,] 0 7 12 15 16 15 12 7 0 291 [2,] 293 0 5 8 9 8 5 0 293 284 [3,] 288 295 0 3 4 3 0 295 288 279 [4,] 285 292 297 0 1 0 297 292 285 276 [5,] 284 291 296 299 0 299 296 291 284 275 [6,] 285 292 297 0 1 0 297 292 285 276 [7,] 288 295 0 3 4 3 0 295 288 279 [8,] 293 0 5 8 9 8 5 0 293 284 [9,] 0 7 12 15 16 15 12 7 0 291 [10,] 9 16 21 24 25 24 21 16 9 0
Se vede că ignorând ultima coloană şi ultima linie, valorile sunt simetrice faţă de axele centrale ale matricei (şi faţă de centrul acesteia) - descrescând uşor dinspre "vârfurile mari" 299 spre marginea stângă şi respectiv spre marginea dreaptă a matricei şi crescând uşor dinspre vârfurile mici 1 ("conjugate" celor mari) spre marginea superioară şi respectiv, cea inferioară. Matricea respectivă este forma numerică a unor perechi de hiperbole echilatere conjugate.
Ar fi de văzut dacă putem găsi ceva "colorat" (în loc de nuanţe de gri), care să merite atenţie; iată două încercări modeste, de a obţine "decoraţiuni hiperbolice" folosind palete de culori:
W <- 150; G <- W / 2 # pentru a doua imagine, W <- 250 pal <- colors()[1:49] # rainbow(125) raster <- as.raster(outer(1:W, 1:W, function(u, v) pal[1 + ((u - G)^2 - (v - G)^2) %% 49])) # %% 125 plot(raster)



Bineînţeles că urmează alte experimente, pentru alegerea şi filtrarea culorilor; de exemplu, ultima imagine a rezultat extinzând într-un anumit mod, filtrarea din secvenţa de comenzi redată mai sus (prin care obţinusem primele două imagini). Este de subliniat că aceste trei imagini diferă doar prin doi parametri: "W" şi valoarea prin care am modulat diferenţele de pătrate (din formula de selectare a indicilor de culoare).
vezi Cărţile mele (de programare)