Dacă $f(z)=z^3+pz+q,\,z\in\mathbb{C}$ are două rădăcini de modul 1, una fixată şi cealaltă mobilă - atunci locul $\mathcal{P}$ al valorilor parametrului $p$ este o trisectoare (cu axa de simetrie înclinată dublu faţă de rădăcina fixă, axele buclelor având lungimile 1 şi 3); am arătat aceasta în [1], iar acum încercăm să clasificăm şi să caracterizăm locul punctelor critice ale lui $f(z)$.

Rădăcinile derivatei $f'(z)=3z^2+p$ sunt $\small\pm\normalsize\delta\small=\pm\sqrt{-p/3\,}$; dar ignorăm deocamdată, factorul constant $\small-1/\sqrt{3\,}$ şi notăm prin $\mathcal{K}$ locul punctelor $\small\pm\normalsize\sqrt{p\,}$. Punctele de afixe $\delta$ şi $-\delta$ sunt simetrice faţă de origine, încât putem neglija semnul; pe figuri, vom marca prin culori distincte, cele două ramuri simetrice faţă de origine ale lui $\mathcal{K}$.

Putem considera, pentru simplitate, că rădăcina fixă este $z_1=1\,$ (altfel, o rotaţie a planului de unghi $-\arg z_1$ va aduce $z_1$ în 1, iar prin rotaţie forma curbelor nu se modifică); ecuaţiile (1) şi (2) din [1] - care sunt ecuaţii parametrice echivalente, ale curbei $\mathcal{P}$ - devin în acest caz:

$\large p(\theta)=e^{2i\theta}+e^{i\theta}+1\normalsize ,\,\theta\in(-\pi,\pi]\;\;\;\hskip5em (1)$

$\large p(\theta)=e^{i\theta}(2\cos \theta +1)\normalsize ,\,\theta\in(-\pi,\pi]\hskip5em (2)$

cu precizarea că aici am eliminat factorul multiplicativ $-1$ (care ar determina doar simetrizarea faţă de origine - ceea ce nu modifică forma curbelor; în plus, ţinem cont astfel şi de faptul că pentru $\mathcal{K}$ - sub radical - deja am considerat $p$, în loc de $-p$).

$\mathcal{K}$ se obţine transformând prin sqrt() punctele curbei $\mathcal{P}$; în general, prin sqrt() punctul cu raza polară $\rho\gt 0$ şi unghiul polar $\theta$ este transformat în punctul de coordonate polare $(\sqrt{\rho},\,\theta/2)$.

În mod implicit, prin (1) şi (2) obţinem valori de tip complex - deci calculul radicalului va implica funcţia complexă sqrt(). Dar (2) - chiar dacă greşit - ar putea fi interpretată ca "ecuaţie polară" $|2\cos \theta +1|e^{i\theta}$ şi ar fi interesant de văzut ce se întâmplă dacă folosim (2) şi astfel (cu abs()).
În programul următor definim câte o funcţie pentru (1) şi respectiv, pentru ecuaţia polară "dedusă" din (2) şi o funcţie care plotează pentru fiecare dintre aceste două cazuri, locurile $\mathcal{P}$ şi $\mathcal{K}$ (evidenţiind şi nişte raze polare particulare; omitem aici, comenzile de etichetare):

tris1 <- function(u) exp(2i*u) + exp(1i*u) + 1  # ecuaţia (1) a curbei P
tris2 <- function(u) exp(1i*u) * abs(2*cos(u)+1)  # ecuaţia polară "dedusă" din (2)

plot_loci <- function(tris) {
  plot(0,0, type="n", xlim=c(-3, 3), ylim=c(-3, 3), asp=1)
  u <- seq(-pi, pi, length=6001)  # un eşantion de unghiuri
  P <- tris(u)  # punctele trisectoarei (fie prin (1), fie prin "ecuaţia polară")
  points(P, type="l", lwd=0.7, col="red") 
  K <- sqrt(P)  # ramura cu "+" a curbei K
  points(K, type="l", lwd=0.9, col="blue")
  points(-K, type="l", lwd=0.8, col="magenta")  # ramura cu "-"
  # A <- tris(pi/4); A1 <- sqrt(A); 
  ## marchează puncte particulare, etichetează, adnotează
}

Setând un panou grafic cu un rând şi două coloane şi apelând plot_loci(tris1) şi apoi plot_loci(tris2) - obţinem imaginea următoare:

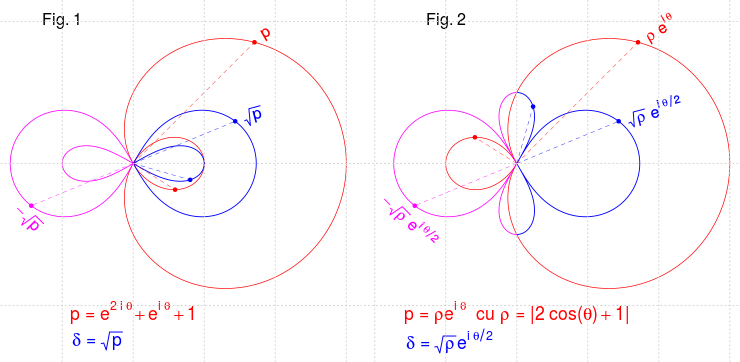
Am evidenţiat cumva mai sus, că nu prea este corect să considerăm ecuaţia parametrică (2) ca "ecuaţie polară" - cum am făcut totuşi în program, pentru Fig.2 - şi ni se pare clar că Fig.1 (şi nu Fig.2) reprezintă "corect" trisectoarea $\mathcal{P}$ (curba roşie) şi curba $\mathcal{K}$ (cu ramurile albastru şi magenta, simetrice faţă de origine). Dar singura deosebire între cele două figuri, constă în poziţionarea buclei mici, atât pentru trisectoare cât şi pentru $\mathcal{K}$.

Este greu de catalogat curba $\mathcal{K}$, dar Fig.2 ar avea un avantaj: curba albastru-magenta evocă intuitiv categoria denumită trisectoarea lui Ceva, notată aici cu $\mathcal{T}$. Fig.3 arată o proprietate caracteristică a curbei $\mathcal{T}$: dacă $O$ este centrul curbei, $d$ este axa mare a ei, iar $R\in\mathcal{T}$, atunci unghiul dintre $OR$ şi $d$ este a treia parte din unghiul lui $RN$ cu $d$ - unde $N\in d$ este construit astfel încât $OM=MN=NR$ (= 1, în Fig.3), $M$ fiind intersecţia dintre $OR$ şi cercul de centru $O$, cu raza egală cu a treia parte din lungimea axei mari.

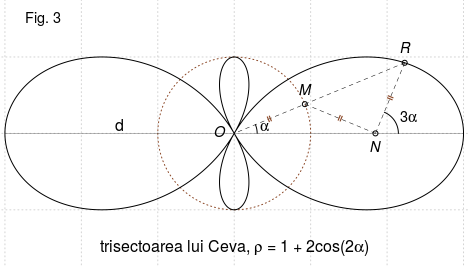
Avem $\small\measuredangle RMN=2\alpha$ (ca unghi exterior triunghiului isoscel $\small OMN$), deci $\small MR=2\cos 2\alpha$ (ca bază a triunghiului isoscel $\small MNR$); rezultă că raza polară $\small OR\normalsize =1+2\cos 2\alpha$ (presupunând $\small OM=1$).

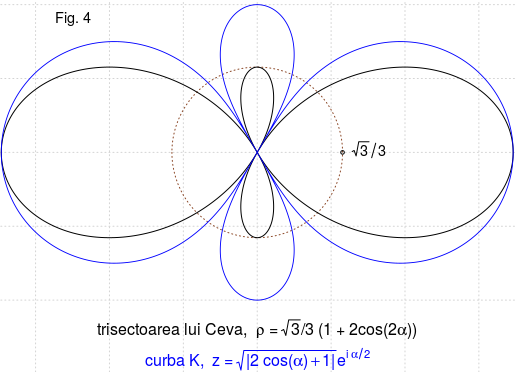
În Fig.4 am considerat $\small OM=\sqrt{3\,}/3$, având în vedere că axa mare a curbei $\mathcal{K}$ are lungimea $\small\sqrt{3\,}$. Confruntând vizual cele două curbe din Fig.4, putem spune că intuiţia ne-a cam înşelat: $\mathcal{K}$ nu este o trisectoare Ceva. Totuşi, să observăm analogia dintre banda cuprinsă între buclele mari ale lui $\mathcal{K}$ şi $\mathcal{T}$ şi banda cuprinsă între un cerc şi o elipsă având ca axă mare un diametru al cercului; ştim că în acest din urmă caz, raportul ordonatelor a două puncte aflate pe o aceeaşi verticală, unul pe cerc şi celălalt pe elipsă, este constant - încât ar fi de aşteptat cumva, ca raportul analog pentru primul caz să fie deasemenea, constant…

Cu alte cuvinte, intuim că scalând ordonatele punctelor buclei mari a curbei $\mathcal{T}$ cu un anumit factor constant, vom obţine o buclă care se suprapune (eventual - cu diferenţe neglijabile) peste bucla mare a curbei $\mathcal{K}$. Dar o investigare analitică a existenţei factorului constant respectiv, deja ni se pare complicată; preferăm să probăm experimental, adaptând programul de mai sus cum descriem în continuare.

Dacă raportul de ordonate $Y_K(x)\,/\,Y_T(x)$ nu depinde de abscisa $x$ la care este măsurat (cum presupunem), atunci luând $x=1$, avem factorul constant căutat. Dar punctele curbelor sunt obţinute în vectorii respectivi prin formule de tip polar, deci este mai greu de identificat punctele lor de o aceeaşi abscisă - aşa că procedăm "pe dos": generăm prin seq() un număr aşa de mare (am ajuns la 100000) de unghiuri, încât să avem şansa de a obţine şi puncte (ale curbelor) cu abscise suficient de apropiate de 1; apoi, căutăm în vectorii respectivi (şi alegem) puncte cu partea reală cât mai apropiată de 1:

raza <- sqrt(3)/3
u <- seq(-pi, pi, length=99999)
Tc <- raza*(1 + 2*cos(2*u))*exp(1i*u)  # T (Ceva)
points(Tc, type="l")
P <- abs(2*cos(u)+1)*exp(1i*u)
K <- sqrt(P)  # curba K
points(c(K,-K), type="l", lwd=0.9, col="blue")
# K[abs(Re(K)-1) < 1e-6]    ## 0.9999996+0.7493683i ...
# Tc[abs(Re(Tc)-1) < 1e-4]  ## 1.000024+0.57735i ...
CONST <- 0.7493683 / 0.57735  # ≈ y_K / y_T
points(Re(Tc), Im(Tc)*CONST, pch='.', col="red") 

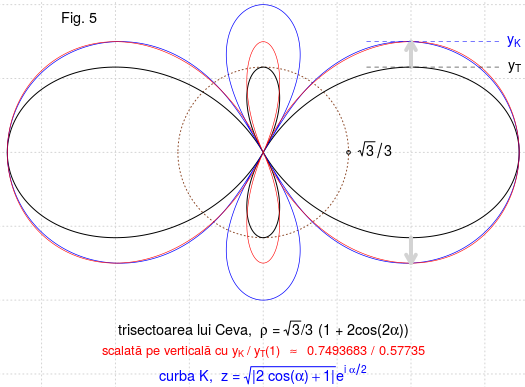
Curba roşie din Fig.5 reprezintă rezultatul scalării pe verticală cu factorul "constant" evidenţiat în program, a curbei $\mathcal{T}$; se poate observa (mărind imaginea) că bucla mare a ei şi bucla mare (albastră) a curbei $\mathcal{K}$ sunt într-adevăr foarte apropiate, dar nu coincid (cu alte cuvinte, cele două bucle pot fi suprapuse doar aproximativ, printr-o scalare verticală; factorul care asigură "cea mai bună" suprapunere este probabil, cel determinat în program - corespunzător abscisei 1, pentru care valoarea $Y_K$ este maximă).

Se pare că trebuie să abandonăm ideea de a depista în cataloage, o curbă "clasică" pe care să o putem asocia (fără aproximări) cu $\mathcal{K}$; ne rămâne eventual, să încercăm un studiu independent al proprietăţilor acestei curbe.

Probabil că un asemenea studiu trebuie să plece "mai de jos", caracterizând întâi radicalul unui cerc care trece prin origine. Într-adevăr, (1) se poate scrie $p(\theta)=(e^{i\theta}-\omega)(e^{i\theta}-\overline{\omega})$, unde $\omega=e^{2\pi i/3}$; cei doi factori reprezintă câte un cerc de rază 1 care trece prin origine. Se poate constata (printr-un program similar celui de mai sus) că radicalul unui astfel de cerc are o buclă foarte asemănătoare cu bucla mare a lui $\mathcal{K}$ (iar plotând produsul radicalilor celor doi factori, obţinem - ca şi plotând radicalul produsului (nedescompus în factori, ca mai sus) - chiar curba $\mathcal{K}$).