Model C++ de graf şi submodel de graf eulerian
Reluăm modelul de Graph din [1], completându-l astfel încât să facilităm algoritmii care angajează muchiile grafului: după ce muchia este parcursă, ea trebuie "ştersă" (marcând-o drept "utilizată"), iar gradele curente ale capetelor ei trebuie decrementate.
Model de graf neorientat
De data aceasta considerăm numai cazul grafurilor neorientate; nu angajăm deocamdată, "costuri" numerice asociate muchiilor.
/** graph.h Grafuri neorientate; noduri numerotate consecutiv, de la 0 Definirea adiacenţei: a folosi metoda addEdge() "Afişare": to_DOT() produce un fişier .dot **/ #include <vector> #include <map> typedef std::vector<int> Bin; // "dulap" pentru adiacenţi typedef Bin::iterator Bin_it; // "pointer" de adiacenţi ai vârfului typedef std::map<std::pair<int,int>, bool> Edges; // <u,v>: false (vom impune u < v) typedef Edges::iterator Edges_it; class Graph { // neorientat, cu vârfurile 0..V-1 public: Graph(int V): V(V), adj(new Bin[V]) { degree.assign(V, 0); } ~Graph() { delete [] adj; } void addEdge(int, int); // adaugă muchie neutilizată; grade curente void delEdge(int, int); // marchează muchia ca "utilizată" virtual int descend(int); // alege o muchie "neutilizată" void to_DOT(const char*); // fişier DOT (pentru imagine grafică) void DFS(int, std::vector<bool>&); // Depth-first-search virtual void process(int) {} // prelucrează din DFS() nodul vizitat protected: // clasele derivate vor putea accesa direct datele int V; // numărul de vârfuri Bin *adj; // adj[w] = lista adiacenţilor lui w, w=0..V-1 Bin degree; // gradele curente (afectate de delEdge()) Edges used_edges; // muchiile (utilizate/neutilizate) [u,v] cu u < v }; // produce o pereche ("muchie") ordonată crescător inline std::pair<int,int> make_edge(const int u, const int v) { return (u < v? std::make_pair(u, v): std::make_pair(v, u)); }
Constructorul doar alocă memorie, pentru înregistrarea ulterioară a adiacenţei specifice problemei (fiecărui vârf fiindu-i alocat câte un vector al adiacenţilor săi) şi deasemenea, pentru un vector în care vor fi actualizate gradele curente ale vârfurilor; degree[u] > 0 va indica faptul că ajungând în vârful u, există continuare pe o muchie care n-a fost parcursă anterior.
map-ul used_edges permite marcarea muchiilor parcurse (şi testarea eficientă a stării curente). addEdge(v, w) (liniile 6-15, mai jos) serveşte pentru înscrierea ca "adiacente" a două noduri: dacă [v,w] n-a fost înscrisă anterior (linia 8), atunci fiecare dintre cele două noduri este adăugat în lista adiacenţilor celuilalt, li se incrementează gradele curente şi se adaugă muchia nouă în used_edges, marcând-o ca "neutilizată". Muchia respectivă este constituită (linia 7) invocând funcţia utilitară make_edge(); aceasta produce o pereche ordonată crescător - evitând să înscriem şi [u,v] şi [v,u].
delEdge() "şterge" o muchie: o marchează în used_edges ca fiind "utilizată" şi decrementează gradele curente ale capetelor ei; iar descend() (liniile 22-27) serveşte la extinderea unui traseu printr-o muchie "neutilizată". Fiind declarată "virtual", descend() va putea fi redefinită într-o clasă derivată, încât alegerea muchiei să depindă şi de un criteriu specific.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | /** graph.cpp **/ #include "graph.h" #include <iostream> #include <fstream> void Graph::addEdge(int v, int w) { std::pair<int,int> edg = make_edge(v, w); // v<w? <v,w> : <w,v> if(used_edges.find(edg) == used_edges.end()) { // [v,w] nu există adj[v].push_back(w); // w este adiacent lui v adj[w].push_back(v); // v este adiacent lui w degree[v]++; // actualizează gradele celor două vârfuri degree[w]++; used_edges[edg] = false; // adaugă [v,w] (ca "neutilizată") } } void Graph::delEdge(int v, int w) { used_edges[make_edge(v,w)] = true; // marchează ca "utilizată" degree[v] --; degree[w] --; // actualizează gradele curente } int Graph::descend(int u) { // caută un adiacent v cu [u,v] "neutilizată" for(Bin_it ui=adj[u].begin(); ui != adj[u].end(); ++ui) if(! used_edges[make_edge(u, *ui)]) return *ui; return -1; } // "afişează" graful într-un fişier DOT (ignorând însă, vârfurile izolate) // Pentru imagine grafică: `dot -Tpng -o filename.png filename.dot` void Graph::to_DOT(const char* filename) { std::ofstream out(filename); out << "graph G {\n"; // graf neorientat for(Edges_it pe = used_edges.begin(); pe != used_edges.end(); ++pe) { std::pair<int,int> edge = (*pe).first; out << edge.first << "--" << edge.second << ";\n"; } out << '}'; } // parcurge (şi eventual evaluează nodurile) "în adâncime" void Graph::DFS(int v, std::vector<bool>& visited) { visited[v] = true; process(v); // a defini după caz, în clasele derivate for (Bin_it i = adj[v].begin(); i != adj[v].end(); ++i) if (!visited[*i]) DFS(*i, visited); } |
to_DOT() (linia 31) produce un fişier DOT (vezi [1]), parcurgând used_edges; dacă este cazul, nodurile izolate (nefiind reflectate în "used_edges") trebuie adăugate manual.
DFS() este aceeaşi ca în [1]. Ar fi de luat în seamă ideea de a modifica testul din linia 46, adăugând && !used(muchia_curentă)) - astfel încât parcurgerea în adâncime să depindă de o metodă virtuală used() (o clasă derivată putând astfel să impună limitarea parcurgerii, la muchiile "neutilizate"); dar ni se pare mai simplu (şi mai eficient) să separăm între vârfuri şi muchii - cum ne-am şi angajat de la bun început, definind "Bin"[] pentru vârfuri şi "Edges" pentru muchii şi prevăzând degree[] pentru a menţine o anumită legătură (suficientă şi eficace) între acestea şi cursul parcurgerii.
Derivarea grafurilor euleriene (algoritmul lui Hierholzer)
Extindem clasa definită mai sus, adăugând o metodă care testează dacă graful respectiv este eulerian şi una care determină un ciclu/lanţ eulerian, înscriindu-l într-un anumit vector:
/** egraph.h graf eulerian (derivat din Graph) **/ #include "graph.h" class Egraph: public Graph { public: Egraph(int n): Graph(n) {} ~Egraph() {} int have_tour(); // eulerian? (foloseşte Graph::DFS()) void find_tour(int); // găseşte ciclu/lanţ eulerian void print_tour(); private: Bin tour; // înregistrează un drum/ciclu eulerian }; // predicat utilizat la contorizarea nodurilor de grad impar inline bool is_odd(const int n) { return (n & 1); } enum {CYCLE=-1, NECONEX=-2, MANY_ODD=-3}; typedef std::vector<int>::reverse_iterator Rev_it; // tour[] va fi parcurs în sens invers
Hierholzer a demonstrat (prin 1870) că un graf neorientat (conex) este eulerian dacă şi numai dacă el are cel mult două vârfuri de grad impar. Dacă toate vârfurile au grad par, atunci există un ciclu care conţine fiecare muchie câte o singură dată; dacă există două (şi numai două) vârfuri de grad impar, atunci există un lanţ care le uneşte şi care conţine toate muchiile, câte o singură dată.
Metoda have_tour() apelează Graph::DFS() pentru a stabili dacă graful respectiv este conex; dacă da - atunci determină numărul de vârfuri de grad impar (linia 12, mai jos) şi dacă acesta este 2, atunci returnează primul dintre cele două (linia 17), iar altfel - se returnează (liniile 11, 15, 19) una dintre cele trei valori negative enumerate în "egraph.h".
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | /** egraph.cpp **/ #include "egraph.h" #include <algorithm> // find(), find_if(), count_if() #include <iostream> #include <stack> // e nevoie de o stivă, pentru a depista şi descărca ciclurile int Egraph::have_tour() { std::vector<bool> used(V, false); DFS(0, used); // Graph::DFS() if(find(used.begin(), used.end(), false) != used.end()) return NECONEX; // nu este graf conex int c_odd = count_if(degree.begin(), degree.end(), is_odd); switch(c_odd) { case 0: // există cicluri euleriene return CYCLE; case 2: // drum eulerian (între nodurile de grad impar) return (find_if(degree.begin(), degree.end(), is_odd) - degree.begin()); default: // graf conex neeulerian return MANY_ODD; } } void Egraph::find_tour(int u) { // Carl Hierholzer, 1873 std::stack<int> cycle; // evidenţiază câte un ciclu al grafului cycle.push(u); while(! cycle.empty()) { int u = cycle.top(); while(degree[u] > 0) { // există [u,v] "neutilizată" int v = descend(u); cycle.push(v); // trece prin v delEdge(u, v); // "şterge" [u,v] şi actualizează gradul curent u = v; // trasează mai departe din nodul v } // Descarcă de pe `cycle` nodurile din care nu mai există muchii neutilizate // şi expandează `cycle` dintr-un nod care încă are gradul curent nenul. while(! cycle.empty() && (degree[cycle.top()] == 0)) { int u = cycle.top(); cycle.pop(); tour.push_back(u); // ciclul este înregistrat invers (de la sfârşit) } } } void Egraph::print_tour() { // tour[] conţine ciclul/drumul eulerian inversat for(Rev_it it=tour.rbegin(); it != tour.rend(); ++it) std::cout << *it << " "; std::cout << '\n'; } |
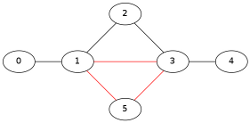
Ilustrăm pe un exemplu simplu, funcţionarea metodei find_tour():
top: push: în stivă: pop:
0 1 2 3 4 0,1,2,3,4 4
3 5 1 3 0,1,2,3,5,1,3 3 1 5 3 2 1 0
find_tour(0) pune nodul 0 pe stiva "cycle" (liniile 24-25) şi apoi (în bucla 28-33) adaugă în stivă nodurile 1, 2, 3 şi 4 ("ştergând" muchiile parcurse).
Din nodul 4 ("top"-ul stivei) nu se mai poate avansa pe o muchie "neutilizată" şi urmează bucla din liniile 36-40 - descărcând din stivă nodul 4. Reluând bucla 28-33 din nodul 3 ("top"-ul curent al stivei), se extinde stiva cu 5,1,3; acum din 3 nu se mai poate continua (degree[3] a coborât la 0) şi urmează iarăşi bucla 36-40, în care se descarcă acum toată stiva (toate gradele curente ale nodurilor au ajuns 0) - rezultând în final, lanţul eulerian [0, 1, 2, 3, 5, 1, 3, 4].
Cicluri euleriene în grafuri complete de ordin impar
Grafurile complete de ordin impar sunt (evident) grafuri euleriene şi - fiind uşor de generat - ne pot servi pentru a "testa" definiţiile de mai sus, inclusiv în privinţa eficienţei. Următorul "client" main() construieşte un graf complet de ordinul indicat la apel şi angajează metodele din Egraph pentru a produce eventual, un ciclu eulerian al acestuia:
#include "egraph.h" #include <iostream> #include <cstdlib> // atoi() using namespace std; int main(int argc, char* argv[]) { int n = argc > 1? atoi(argv[1]):5; // defineşte un graf complet de ordinul n (vârfuri 0..n-1) Egraph K(n); for(int i=0; i < n-1; ++i) // oricare două vârfuri sunt adiacente for(int j=i+1; j < n; ++j) K.addEdge(i, j); K.to_DOT("K.dot"); // `dot -Tpng -Kcirco -o K.png K.dot` int has = K.have_tour(), from = -1; switch(has) { case NECONEX: cout << "neconex\n"; break; case MANY_ODD: cout << "conex neEulerian\n"; break; case CYCLE: cout << "ciclu Eulerian:\n"; from = 0; break; default: cout << "lanţ Eulerian:\n"; from = has; break; } if(from != -1) { K.find_tour(from); K.print_tour(); } }
Bineînţeles că în cazul grafurilor complete, puteam evita testul have_tour(): pentru n par avem "neeulerian", iar altfel lansăm find_tour() dintr-un vârf oarecare; dar formularea generală redată poate fi adaptată uşor pentru oricare alt graf, schimbând doar definiţia preliminară a adiacenţei.
Compilăm şi executăm, pentru o primă testare a funcţionării:
vb@vb:~/EGRAPH$ g++ graph.cpp egraph.cpp egraph_test.cpp -o etest vb@vb:~/EGRAPH$ ./etest 7 ciclu Eulerian: 0 1 2 0 3 1 4 0 5 1 6 2 3 4 2 5 3 6 4 5 6 0
Pentru o cea mai modestă testare de "eficienţă", putem folosi utilitarul time (am evitat afişarea finală a ciclului, comentând linia "print_tour()" şi recompilând programul):
vb@vb:~/EGRAPH$ time ./etest 55 // pentru graful K55
real 0m0.040s
user 0m0.032s
sys 0m0.004s
Timpul de execuţie rămâne sub o secundă până pe la n=165 (K163) şi este sub 2 secunde până pe la n=201; pentru n=301 - aproape 7 secunde, pentru n=401 - 17 secunde şi timpul de execuţie rămâne sub 1 minut până pe la n=601. Rezultatele sunt "onorabile", dar le-am putea confrunta şi cu cele obţinute rulând diverse alte programe care ne dau cicluri euleriene.
Pe de altă parte, timpii de execuţie devin mult mai buni dacă recompilăm programul cu opţiunea -O3 (care determină optimizări importante, asupra codului generat): astfel, pentru K601 obţinem numai 12 secunde (faţă de 59 secunde), iar K1001 (cu 500500 muchii) este rezolvat sub 100 de secunde.
Investigând mai amănunţit funcţionarea metodei find_tour(), vom putea deduce - cum vom arăta într-un studiu separat - anumite caracteristici structurale ale ciclului eulerian furnizat de algoritmul lui Hierholzer pentru K2n+1 - rezultând în fond o formulare directă (sau "imediată") a unuia dintre ciclurile euleriene, pentru oricare graf complet de ordin impar.
vezi Cărţile mele (de programare)