Să zicem că avem un punct mobil, iar coordonatele polare ale acestuia variază în funcţie de un acelaşi parametru; judecând sau observând cum creşte sau descreşte raza polară (când am roti-o în jurul originii), putem schiţa locul geometric al punctului respectiv.

Ce curbă descrie punctul de afix $z(z+1)$, dacă $|z|=1$? Altfel formulat, avem de caracterizat transformata cercului unitate prin funcţia $f(z)=z(z+1),\,z\in\mathbb{C}$.

Punctele cercului $|z|=1$ se pot exprima prin $z=\cos \theta + i\sin \theta=e^{i\theta},\,\theta\in(-\pi,\pi]$. Avem $z(z+1)=e^{2i\theta} + e^{i\theta}=p(\theta)$ şi observând că putem obţine $p(\theta)$ adunând vectorii de poziţie $(1, \theta)$ şi $(1, 2\theta)$ - găsim uşor o exprimare a coordonatelor polare $(\rho, \varphi)$ prin parametrul $\theta$:

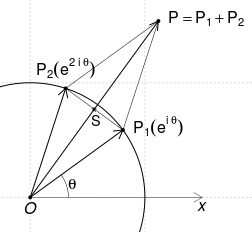
$\small OP_1=OP_2=1\normalsize\Rightarrow \small OP_1PP_2$ este un romb (unde $\small\overline{OP}$ este suma vectorilor $\small\overline{OP_1}$ şi $\small\overline{OP_2}$);
deci $\small\measuredangle P_1OP=\theta/2$ şi rezultă $\varphi\small=\measuredangle xOP\normalsize=3\frac{\theta}{2}$.

Apoi, $\small S$ fiind mijlocul coardei $\small P_1P_2$, avem:
$\rho\small=OP=2\,OS\normalsize=2\cos\frac{\theta}{2}$.

Când vectorul $\small\overline{OP_1}$ se roteşte în sens antiorar în jurul originii (plecând de la axa polară $\small Ox$) cu unghiul $\theta$, coordonatele polare ale punctului $P$ sunt $(\rho=2\cos \frac{\theta}{2},\,\varphi=3\frac{\theta}{2})$; să observăm că prin inversarea sensului de rotire, $\rho$ nu se modifică, iar $\varphi$ îşi schimbă doar semnul (direcţiile $\pm\theta$ sunt simetrice faţă de axa $Ox$ şi au aceeaşi valoare a cosinusului). Rezultă că locul punctului $P$ este simetric faţă de axa $Ox$ şi este suficient să analizăm numai intervalul $\theta\in[0, \pi]$.

Pe intervalul $[0,\pi]$ derivata $\rho'(\theta)=-\sin\frac{\theta}{2}$ este negativă, deci raza polară $\rho$ descreşte de la valoarea $\rho(0)=2$ către valoarea $\rho(\pi)=0$; putem "schiţa" punctele corespunzătoare:

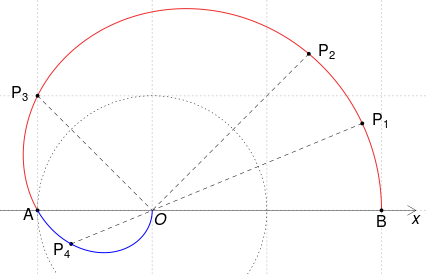
Când $\theta$ creşte de la $0$ la $2\pi/3$, unghiul $\varphi$ creşte şi el, de la $0$ la $\pi$, iar $\rho$ descreşte de la $2$ la $1$ - astfel că $P(\rho,\varphi)$ descrie arcul roşu, plecând din $B(2,0)$ şi ajungând în $A(1, \pi)$ (micşorând mereu raza $\rho$).

Când $\theta$ creşte de la $2\pi/3$ la $\pi$, unghiul $\varphi$ creşte de la $-\pi$ la $-\pi/2$, iar $\rho$ descreşte de la $1$ la $0$ - încât $P$ descrie arcul marcat cu albastru, dinspre $A$ spre $O$.

De exemplu, pentru $\theta=\pi/12$ obţinem punctul $P_1(\rho=2\cos\frac{\pi}{24}\approx 1.98, \varphi=\frac{\pi}{8})$; pentru $\theta=\pi/6$ avem $P_2(\rho=2\cos\frac{\pi}{12}\approx 1.93, \varphi=\frac{\pi}{4})$; cu $\theta=\pi/2$ avem $P_3(\sqrt{2\,}, \frac{3\pi}{4})$; iar pentru $\theta=3\pi/4$ avem (pe arcul albastru) $P_4(\rho=2\cos\frac{3\pi}{8}\approx 0.765, \varphi=-\pi/8)$.

Simetrizând curba trasată mai sus (pentru $\theta\in[0,\pi]$) faţă de axa $Ox$, obţinem o curbă care s-ar încadra în familia denumită generic "melcul lui Pascal" - dacă (şi ne rămâne să verificăm) sunt îndeplinite anumite proprietăţi caracteristice. Vom demonstra mai jos următoarele proprietăţi (care atestă încadrarea curbei "construite" prin iterarea unghiului polar mai sus, în categoria trisectoare Pascal - caz particular de "melc Pascal"):

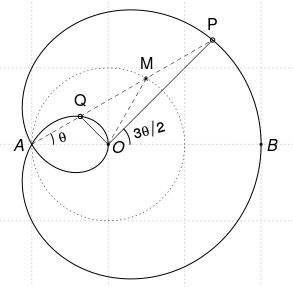
Punctele $A=p(2\pi/3)$, $P=p(\theta)$, $Q=p(\theta+\pi)$ sunt coliniare (amintim că $p(\theta)=e^{2i\theta}+e^{i\theta}$).

Mijlocul $M$ al segmentului $PQ$ este situat pe cercul unitate; $\small MQ=MP=MO$ (= 1) şi $\small OP\perp OQ$.

$\measuredangle PAB$ este a treia parte din dublul unghiului $\measuredangle POB$.

Cum am văzut deja mai sus, punctul $A$ are coordonatele polare $(\rho=1, \varphi=\pi)$ şi din $\varphi=3\theta/2$ avem $\theta=2\pi/3$; cu alte cuvinte, $A$ are afixul $p(2\pi/3)$ (unde $p(\theta)=e^{2i\theta} + e^{i\theta}$). Notăm cu $P$ şi $Q$ punctele curbei de afixe $p(\theta)$ şi respectiv $p(\theta+\pi)$ (ţinând cont de simetria curbei faţă de $Ox$ este suficient să luăm $\theta\in[0,\pi]$).

Pentru a demonstra că punctele $A$, $P$ şi $Q$ sunt coliniare, să ţinem seama de faptul că un vector oarecare poate fi reprezentat (ca mărime, direcţie şi sens) de diferenţa afixelor extremităţilor. Avem: $\small\overline{AP}=p(\theta)-p(2\pi/3)=e^{2i\theta}+e^{i\theta}+1\normalsize=e^{i\theta}(e^{i\theta}+1+e^{-i\theta})$ şi $\small\overline{AQ}=p(\theta+\pi)-p(2\pi/3)=e^{2i\theta}-e^{i\theta}+1\normalsize=e^{i\theta}(e^{i\theta}-1+e^{-i\theta})$; pe de altă parte, avem $e^{i\theta}+e^{-i\theta}=2\cos \theta$ (număr real). Rezultă că există factorul real $t=\frac{2\cos\theta+1}{2\cos\theta-1}$ astfel încât $\small\overline{AP}=t\,\overline{AQ}$ (exceptând $\theta=\pi/3$, când $Q$ ajunge în $A$); prin urmare, punctele $A$, $Q$ şi $P$ ($Q\ne A$) sunt într-adevăr, coliniare.

Mijlocul $M$ al segmentului $PQ$ are afixul $\frac{1}{2}(p(\theta)+p(\theta+\pi))=e^{2i\theta}$, deci $M$ este situat pe cercul unitate $|z|=1$; fiindcă $M$ este egal depărtat de $Q$, $P$ şi $O$, rezultă şi că triunghiul $QOP$ (când $Q\ne O$) este dreptunghic în $O$ (şi $\small PO^2+QO^2 =(2\,OM)^2=4$). Fiindcă $PMO$ şi $MOA$ sunt triunghiuri isoscele, avem $\small\measuredangle APO=\theta/2$ şi rezultă că $\measuredangle POB \small= \theta+\theta/2\normalsize=3\,\theta/2$.

Este verificată astfel, o construcţie cunoscută a punctelor trisectoarei Pascal: se consideră un cerc de rază $r$ (în cazul nostru 1) şi un punct fixat $A$ al acestuia; se trasează drepte $AM$, $M$ fiind un punct oarecare al cercului; pe $AM$ se marchează punctele $P$ şi $Q$ încât $MP=MQ=r$; atunci $P$ şi $Q$ parcurg împreună cele două bucle ale trisectoarei.

Deasemenea, este verificată şi proprietatea care justifică denumirea de "trisectoare": $\measuredangle PAB$ este a treia parte din dublul unghiului $\measuredangle POB$.

Îndeplinind aceste proprietăţi, locul punctelor $z(z+1)$ când $|z|=1$ este o trisectoare Pascal. Altfel spus, funcţia complexă $f(z)=z(z+1)$ transformă cercul unitate într-o trisectoare Pascal.

Avem o consecinţă interesantă (de fapt… punctul de plecare al problemei tratate mai sus - v. [1]):

Locul geometric al valorilor parametrului complex $p$ al ecuaţiei $z^3+pz+q=0,\,z\in\mathbb{C}$, când o rădăcină este fixată şi o a doua este mobilă pe un acelaşi cerc cu centrul în origine, este o trisectoare Pascal (cu axa de simetrie dată de dublul direcţiei rădăcinii fixe).

Într-adevăr, presupunând rădăcina fixă $z_1=1$ şi $|z_2|=1$ (rădăcina mobilă) şi ţinând seama că $z_1+z_2+z_3=0$, avem $p=z_1z_2+z_1z_3+z_2z_3=-1+z_2z_3=-1-z_2(z_2+1)$ - deci locul lui $p$ se obţine din locul lui $z(z+1)$ cu $|z|=1$, prin simetrizare faţă de origine şi apoi, translatare orizontală cu o unitate.