Pentru recuperare (de exemplu… ce ştim noi despre "funcţia de gradul doi"?!), clarificare, plăcerea firească de a citi şi descoperi (pe cât mă pricep) etc. – răsfoiesc din când în când cărţi devenite "clasice", care se pot obţine eventual de la Internet Archive, sau Google Books etc.

Pe la 1830, Jakob Steiner introducea noţiuni de bază pentru geometria "modernă": fascicule de drepte şi diviziuni de puncte, pricipiul dualităţii şi metode "proiective" de generare a conicelor; proprietăţi de această natură sunt exprimate cu mult farmec în unele cărţi vechi, cum ar fi tratatul lui Michel Chasles "Traité des sections coniques" (1865), din care citez două rezultate (menţionate chiar în primul capitol):

"(7) Les points de rencontre de deux tangentes fixes à une conique et d'une troisième tangente mobile forment deux divisions homographiques." [O tangentă mobilă pe o conică determină pe două tangente fixe ale acesteia, diviziuni omografice]
şi reciproc:
"(9) La courbe, enveloppe des droites qui joignent deux à deux les points homologues de deux divisions homographiques faites sur deux droites, est une section conique tangente à ces deux droites." [Înfăşurătoarea dreptelor duse prin punctele omoloage a două diviziuni omografice de pe două drepte date este o conică tangentă acestora.]

În [1] am formulat o anumită particularizare elementară a acestor proprietăţi:

Dacă $P$, $Q$ şi $H$ sunt puncte necoliniare şi dacă punctele $U$ şi $V$ împart segmentele orientate $\overline{PH}$ şi $\overline{HQ}$ într-un acelaşi raport $t\in\mathbb{R}$, atunci punctul care împarte $\overline{UV}$ în raportul $t$ descrie (când $t$ variază) o parabolă, tangentă dreptelor $PH$ şi $QH$.

În principiu, $U$ şi $V$ determină o corespondenţă omografică între cele două drepte pe care le parcurg, deci după (9), $UV$ înfăşoară o conică (şi ar rămâne de justificat faptul că este chiar o parabolă).
Dar în [1] am iniţiat o demonstraţie directă; încercăm acum să încheiem lucrurile, în cadrele şi spiritul matematicii şcolare.

Punctul care împarte $\overline{UV}$ în raportul $t$ este $z(t)=(1-t)\mathsf{U}+t\mathsf{V}$ (notând cu litere drepte afixele punctelor omonime, care sunt notate italic). Fiindcă $U$ împarte $\overline{PH}$ în raportul $t$, avem $\mathsf{U}=(1-t)\mathsf{P}+t\mathsf{H}$; analog, $\mathsf{V}=(1-t)\mathsf{H}+t\mathsf{Q}$. Rezultă:

Sub această formă (dar cu $t\in[0,1]$) (1) reprezintă o curbă Bézier pătratică (v. [1]), definită de capetele $P$ şi $Q$, cu punctul de control $H$. Să considerăm în loc, forma generală (polinom de variabilă reală, cu coeficienţi complecşi, de gradul doi):

Semnificaţia coeficienţilor

Este încă utilă identificarea cu (1), prin $a=\mathsf{P}+\mathsf{Q}-2\mathsf{H}$, $b=2(\mathsf{H}-\mathsf{P})$ şi $c=\mathsf{P}$. Vedem astfel că $a$ indică direcţia axei parabolei (presupunând că (2) este într-adevăr, o parabolă): $\mathsf{P}+\mathsf{Q}-2\mathsf{H}$ reprezintă vectorul $2\overline{HM}$, unde $M$ este mijlocul coardei $PQ$ – ori ştim că dreapta care uneşte mijlocul unei coarde cu intersecţia tangentelor în capetele acesteia este paralelă cu axa parabolei.
În particular, dacă $a\in\mathbb{R}$ atunci axa parabolei este paralelă cu axa reală $Ox$.

Punctul $P(c)$ aparţine conicei, obţinându-se din (2) pentru $t=0$; iar $b=2(\mathsf{H}-\mathsf{P})$ (reprezentând vectorul $2\overline{HP}$) indică direcţia tangentei în $P$ (fiindcă $z'(0)=b$).
Dar axa parabolei şi tangenta într-un punct oarecare al parabolei nu pot fi paralele; deci pentru (2) este necesară şi condiţia ca raportul coeficienţilor $a$ şi $b$ să nu fie un număr real – altfel, vectorii de poziţie ai punctelor de afixe $a$ şi $b$ ar fi coliniari şi am avea ceva "conică degenerată".
În particular, $a$ şi $b$ nu pot fi ambele, numere reale; de exemplu, $z(t)=2t^2-4t+c$ (pentru oricare $c\in\mathbb{C}$) reprezintă o dreaptă paralelă axei reale (şi însăşi axa reală, dacă $c$ este şi el, număr real: componenta imaginară a valorilor complexe $z(t)$ este în acest caz $y(t)=0$, reprezentând axa $Ox$).

A fi sau a nu fi…

Acum avem de făcut faţă unui aspect delicat: ce să "demonstrăm"?! că (2) este o parabolă? – păi nu ştim din şcoală că "funcţia de gradul doi este o parabolă", cu vârful în punctul de coordonate $(\frac{-b}{2a},\,\frac{-\Delta}{4a})$, etc.?? Ştim şi nu ştim; aici "vârful" menţionat are patru, nu două, "coordonate" (fiindcă $a$, etc. sunt numere complexe)…
$z(t)$ are două "ramuri": $x(t)=a_xt^2+b_xt+c_x$ şi $y(t)=a_yt^2+b_yt+c_y$ (unde $a=a_x+a_yi\in\mathbb{C}$, etc.), fiecare fiind "funcţie de gradul doi" precum ştim din şcoală, reprezentând deci câte o parabolă, dar cumva în "plane" diferite, $Oxt$ şi respectiv $Oyt$; ar fi de arătat că $z(t)$ este o parabolă în sistemul de coordonate $xOy$.

În [1] am considerat (2) într-un caz numeric concret şi am eliminat parametrul $t$, obţinând desigur o ecuaţie de gradul doi în $x$ şi $y$, despre care am constatat (pentru valorile numerice respective) că satisface condiţia necesară pentru a reprezenta o parabolă. Dar fără a concretiza numeric coeficienţii, calculul respectiv este greu de exprimat simbolic, încât nu ne-am înhăma în direcţia eliminării mecanice a lui $t$.

Soluţia simplă vine (probabil) tot "din şcoală": vom fi arătat că (pentru $a,b,c\in\mathbb{R}$), $y=ax^2+bx+c=a\left(x+\frac{b}{2a}\right)^2+\frac{-\Delta}{4a}$ se poate obţine din $Y=X^2$ – compunând translaţia pe $OX$ cu $\frac{b}{2a}$ şi apoi "dilatarea" valorilor prin factorul $a$, cu translaţia pe verticala $OY$ prin $\frac{-\Delta}{4a}$. Şi cum (citând din manualele şcolare) "graficul lui $y=x^2$ se numeşte parabolă", rezultă că $y=ax^2+bx+c$ reprezintă o parabolă (dat fiind că translaţia şi scalarea verticală nu modifică "forma" graficului).
Dar astfel găsim numai parabolele ale căror axe sunt paralele cu $Oy$; implicând în plus, o rotaţie intermediară în jurul originii putem obţine oricare parabolă din plan.

Transformarea afină a parabolei standard

Să procedăm analog, în cazul nostru: să arătăm că există o anumită transformare a planului, care nu alterează proprietăţile calitative ale figurilor şi prin care (2) se poate obţine plecând de la parabola $y=x^2$.

Transformările care "nu alterează proprietăţile calitative" sunt compuse din translaţii, rotaţii, simetrii şi scalări şi au forma generală

De exemplu, $z\mapsto\overline{z}$ simetrizează $z$ faţă de axa reală, iar $z\mapsto\lambda z$ roteşte $z$ în jurul originii cu unghiul dat de argumentul factorului $\lambda$ şi scalează cu modulul acestuia.

(3) păstrează coliniaritatea, paralelismul, raportul de segmente paralele sau coliniare şi transformă o figură într-una "de aceeaşi formă" (de unde şi denumirea de "afinitate", sau transformare afină) – ca şi cum am fi proiectat-o paralel (după o direcţie fixată în spaţiu) pe un alt plan: pătratul devine paralelogram; imaginea unui cerc este o elipsă; o parabolă este dusă tot într-o parabolă, etc.

$a$, $b$ şi $c$ fiind coeficienţii din (2), să particularizăm transformarea (3) astfel:

Prin (4), originea $(0,0)$ ajunge în punctul de afix $c$, punctul unitar $(1,0)$ ajunge în punctul de afix $b+c$, iar punctul $(0,1)$ ajunge în punctul de afix $a+c$.

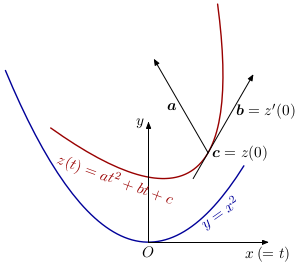
Parabola "standard" $y=x^2$ se reprezintă parametric prin $(x=t, y=t^2)$, deci conţine punctele de afixe $z=t+it^2,\,t\in\mathbb{R}$ şi pentru acestea avem: $\mathcal{T}(z)=\frac{b-ia}{2}(t+it^2)+\frac{b+ia}{2}(t-it^2)+c=at^2+bt+c$ – astfel că $z(t)$ din (2) rezultă ca imagine a parabolei "standard" printr-o transformare afină şi ca urmare (acceptând că transformările afine conservă natura conicelor) este ea însăşi, o parabolă.

În concluzie:
$z(t)=at^2+bt+c,\,t\in\mathbb{R}$ unde $a,b,c\in\mathbb{C}$ sunt afixe de puncte necoliniare, $a\ne 0$ şi $\frac{b}{a}\not\in\mathbb{R}$, reprezintă o parabolă (nedegenerată); axa acesteia are direcţia $\arg a$, iar tangenta în punctul de afix $c$ are direcţia $\arg b$.

Modelarea grafică

Când investigăm şi eventual publicăm o chestiune de matematică, avem două motive pentru a produce figuri: desigur, pentru a oferi un suport vizual faptelor descrise ("partea cititorului"); pe de altă parte (de obicei nepublică - "partea autorului"), figurile permit validarea sau invalidarea unor fapte sau formule rezultate prin calcul lung sau întortocheat şi posibil, defectuos.

Pentru figuri precum cea redată mai sus, am folosit desigur un program în MetaPost – beneficiind de instrucţiuni de trasare a cubicelor Bézier, de tipul de date "transform" care modelează transformările afine, de folosirea unor expresii "cu necunoscute" şi deasemenea, de posibilitatea de a angaja LaTeX pentru a eticheta elementele figurii.
Obs. Pentru investigaţii (inclusiv, "de validare") este preferabil R - pentru uşurinţa cu care pot fi manevrate expresiile cu numere complexe, pentru posibilitatea de "vectorizare" a ecuaţiilor parametrice şi pentru uşurinţa cu care pot fi generate figuri "parametrizate".

Următoarea definiţie MetaPost produce parabola standard $y=x^2$, între capetele ale căror abscise sunt indicate (mai precis, produce o varibilă de tip "path" reprezentând cubica Bézier asociată capetelor şi punctelor de control determinate cum am arătat în [1] - contur care aproximează suficient de exact arcul de parabolă respectiv):

% arcul parabolei y=x^2, de capete date prin abscise (cubică Bézier)
vardef parstd(expr s, r) =
    pair P, Q, H, F, G;
    P = (s, s**2); Q = (r, r**2);  % puncte ale parabolei y=x^2
    H = ((s+r)/2, s*r);  % intersecţia tangentelor în capetele corzii
    F = (2*H + P)/3;  % punctele de control ale cubicei Bézier asociate
    G = (2*H + Q)/3;  % (vezi [1])
    P .. controls F and G .. Q  % arcul parabolei standard, de capete P, Q
enddef;

Introducem transformarea $\mathcal{T}$ dată de (4), dar nu prin formula respectivă (cum ar trebui să facem în alte limbaje), ci indicând transformatele a trei puncte (MetaPost va folosi mecanismul intern de rezolvare a ecuaţiilor liniare, determinând singur cei 6 parametri ai transformării); am prevăzut două posibilităţi – fie furnizăm direct punctele asociate afixelor $a$, $b$ şi $c$ din (2), fie indicăm (în grade) $\arg a$ (adică, după cum am arătat mai sus, direcţia axei parabolei) şi $\arg b$ (adică, direcţia tangentei în $c$):

vardef affinity(expr aPorA, bPorA, cP) =  % 3 puncte, sau 2 unghiuri şi un punct
    save a, b, c, T;  pair a, b, c;  transform T;
    c = cP;
    if pair(aPorA) and pair(bPorA):  % dacă 'a' şi 'b' sunt date ca puncte
        a = aPorA;  b = bPorA;
    else:  % dacă 'a' şi 'b' sunt date implicit, ca valori unghiulare (direcţii)
        a = dir(aPorA);  % 'a'  şi 'b' sunt acum, versorii direcţiilor indicate  
        b = dir(bPorA);
    fi
    (0,0) transformed T = c;         
    (1,0) transformed T = b + c;
    (0,1) transformed T = a + c;
    T  % va transforma y=x^2 în z(t)=at^2 + bt + c (coeficienţi complecşi)
enddef;

Ca exemplu de folosire a acestor definiţii, redăm parţial secvenţa care a produs figura pe care am redat-o mai sus (omitem producerea segmentelor şi etichetelor) :

um = 3cm;  % unitatea de măsură (la trasarea pe pagină a contururilor)
beginfig(2);
    save a, b, c, T, p;  pair a, b, c;  path p[];  transform T;
    T = affinity(120, 60, (0.5,0.75));  % arg(a)=120°; arg(b)=60°; c=.5+.75i
    p0 = parstd(-1.2, 0.8);  % conturul parabolei standard
    p1 = p0 transformed T;  % conturul obţinut aplicând transformarea (4)
    draw p0 scaled um withpen pencircle scaled 1 withcolor .6blue;  % trasează
    draw p1 scaled um withpen pencircle scaled 1 withcolor .6red;
    % ... Alte elemente ale figurii: puncte, săgeţi, etc.; etichete
endfig;

Pentru "prologul" necesar compilatorului ca să implice LaTeX şi pentru calea de urmat pentru a obţine figura în format PDF – vezi [1]. Ni se pare interesant să precizăm că fişierul iniţial, în format EPS, furnizat de compilatorul mpost măsoară peste 103KB (mult, fiindcă au trebuit incluse fonturile matematice folosite de LaTeX pentru cele 8 etichete, unele "lungi", din figură); transformându-l în PDF (prin ps2pdf) a rezultat un fişier de numai aproape 10KB (iar figura de mai sus este o copie ecran după acest fişier PDF, deschis într-un "Document Viewer" – măsurând aproape 20KB).

Elementele parabolei; bănuieli şi investigare grafică

Se cuvine să determinăm, în funcţie de coeficienţii $a$, $b$ şi $c$, vârful $V(v)$ şi focarul $F(f)$ al parabolei (2) (din acestea se pot găsi apoi ecuaţiile axei şi directoarei).
Vom simplifica exprimarea, zicând "punctul $a$" în loc de "punctul de afix $a$" şi "vectorul dat de $a$" în loc de "vectorul de poziţie al punctului de afix $a$".

Tangenta în punctul $z(t)$ are panta $\frac{\mathsf{d}y}{\mathsf{d}x}=\frac{2a_yt\,+\,b_y}{2a_xt\,+\,b_x}$, unde $a=a_x+ia_y$ etc.
Cum am arătat mai sus, axa parabolei (2) are direcţia vectorului dat de $a$; deci panta axei este $\frac{a_y}{a_x}$.
În vârful parabolei, tangenta este perpendiculară pe axă, deci panta tangentei în $V(v)$ este $-\frac{a_x}{a_y}$. Din $\frac{\mathsf{d}y}{\mathsf{d}x}=-\frac{a_x}{a_y}$ găsim valoarea $t^*$ a parametrului $t$ corespunzătoare vârfului $V(v)$ şi apoi, aflăm şi afixul $v$ al acestuia; avem $t^*=-\frac{a_xb_x+a_yb_y}{2(a_x^2+a_y^2)}$, sau (ţinând seama că $a_x=\frac{a+\overline{a}}{2}$ şi $a_y=\frac{a-\overline{a}}{2i}$, etc.), $t^*=-\frac{1}{4}(\frac{b}{a}+\frac{\overline{b}}{\overline{a}})$ (care este număr real, fiind suma dintre un număr complex şi conjugatul său).
Exprimând (2) în "forma canonică" $z(t)=a\left(t+\frac{b}{2a}\right)^2+\frac{-\Delta}{4a}$ (unde $\Delta=b^2-4ac$), putem calcula uşor valoarea $v=\left.z(t)\right|_{t=t^*}$ şi găsim că afixul vârfului parabolei este

Să observăm că ecuaţia

reprezintă punctele unei drepte care trece prin punctul $\frac{-\Delta}{4a}$ şi este paralelă cu vectorul dat de $a$, deci este "paralelă" cu axa parabolei; dar $v$ din (5) satisface (6), anume pentru $t=\frac{1}{16}(\frac{b}{a}-\frac{\overline{b}}{\overline{a}})^2$ – deci "paralela" respectivă trece chiar prin vârful parabolei. Rezultă că (6) este ecuaţia axei parabolei.

(6) exprimă punctele axei considerând ca bază (la $t=0$) punctul fix $\frac{-\Delta}{4a}$ şi ar fi de bănuit că acesta este chiar focarul parabolei (acesta fiind şi singurul punct important al axei, din interiorul parabolei); următorul program R (redat aici cam pe cât se cuvine) ne permite să observăm dacă punctul $F(\frac{-\Delta}{4a})$ satisface sau nu, una dintre proprietăţile caracteristice focarului (proiecţiile focarului pe tangentele parabolei se află pe tangenta în vârful acesteia):

a <- -3-2.2i
b <- 5+1.2i
c <- 1+2i
dt <- b^2 - 4*a*c
f <- -dt/(4*a)  # focarul
v <- a/16 * (b/a - Conj(b/a))^2 + f  # vârful parabolei
Z <- function(t) {  # z(t) pentru o valoare t, sau pentru o secvenţă de valori t
    a*t^2 + b*t + c
}
Zp <- function(t) 2*a*t + b  # derivata lui Z, în t
axa <- function(t) f + a*t   # axa parabolei
tgv <- function(t) v + 1i*a*t  # tangenta în vârf
tgt <- function(t, tau) Z(t) + Zp(t)*tau  # tangenta în punctul Z(t)
prf <- function(t) {  # proiecţia focarului pe tangenta în Z(t)
    0.5*(Z(t)+f) + 0.5*Zp(t)/Conj(Zp(t))*(Conj(f-Z(t)))
}
t_R <- seq(-0.5, 1.5, by=0.01)  # secvenţă de valori pentru parametrul 't'
plot(0, asp=1, type="n", bty="n", cex.axis=0.8, 
     xlim=c(0, 4), ylim=c(0, 4));  grid() # iniţializează fereastra grafică
points(Z(t_R), type="l", lwd=1)  # trasează parabola
points(axa(t_R), type="l", lwd=0.5)  # axa
points(tgv(t_R), type="l", lwd=0.5)  # tangenta în vârf
points(c(v, Z(0), Z(1), Z(0.35)), pch=19, cex=0.4)  # marchează unele puncte
points(f, col="firebrick2", cex=0.5)
text(c(f+0.01+0.03i, v-(0.06+1i*0.01)), labels=c("F", "V"),  #etichetează
     pos=c(1, 4), cex=0.9)
for(h in c(0.35, 0, 1)) {  # trasează tangente (aici, numai 3)
    points(tgt(h, t_R), type="l", lwd=0.5, col="blue")
}
for(h in c(0.35, 0, 1)) {  # marchează proiecţiile focarului pe tangente
    points(prf(h), col="firebrick2", cex=0.4)
}

Se constată, executând acest program, că punctul etichetat cu $F$, de afix $f=\frac{-\Delta}{4a}$, are ca proiecţii ortogonale pe tangentele parabolei, puncte ale tangentei în vârful $V$; figura expune doar cazul a trei tangente, dar puteam marca proiecţiile pe oricâte - adăugând în final for(h in seq(-0.4, 1.4, by=0.1)) points(prf(h), ...).

Desigur, pentru a scrie programul "de investigare" de mai sus, a trebuit să ne amintim câteva "formule matematice": ecuaţia dreptei printr-un punct, de pantă dată; ecuaţia tangentei; calculul afixului proiecţiei unui punct pe o dreaptă. În orice caz, formularea programului şi verificarea bănuielii că $\frac{-\Delta}{4a}$ este chiar focarul parabolei a fost mult mai uşoară, decât demonstrarea cuvenită a acestui fapt.

Formula focarului (demonstraţie)

Să arătăm că $\frac{-\Delta}{4a}$ este focarul parabolei $\mathcal{P}:\;z(t)=at^2+bt+c,\,t\in\mathbb{R}$, $a$, $b$, $c$ fiind afixele unor puncte necoliniare ($a\ne 0$).

Pentru demonstraţie este suficient să arătăm că piciorul perpendicularei din $F(\frac{-\Delta}{4a})$ pe o tangentă oarecare a lui $\mathcal{P}$ este situat pe tangenta în vârf (în punctul $V(v)$ dat de formula (5)).

Fiindcă nu ne place să ţinem minte "pe de rost" diverse formule, să stabilim direct formula principală pe care ne vom baza:

Lema 1. Proiecţia ortogonală a punctului $\alpha$ pe dreapta $d_0:\;z=z_0+at,\,t\in\mathbb{R}$ (unde $\alpha,z_0,a\in\mathbb{C},\,a\ne 0$) are afixul

Demonstraţie. Fie $d_1:\;z=\alpha+ia\tau,\,\tau\in\mathbb{R}$ perpendiculara din $\alpha$ pe $d_0$ ($i^2=-1$ iar $ia$ roteşte $a$ cu 90°, rezultând direcţia perpendiculară celeia date de $a$). Punctul comun $p$ al dreptelor $d_0$ şi $d_1$ satisface ambele ecuaţii – dar în general, nu pentru o aceeaşi valoare a parametrului – şi prin scădere găsim $t-i\tau=\frac{\alpha-z_0}{a}$ şi apoi prin conjugare, $t+i\tau=\frac{\overline{\alpha-z_0}}{\overline{a}}$ – din care, prin adunare, se elimină $\tau$; înlocuind valoarea rezultată astfel pentru $t$ în $p=z_0+at$, ajungem la expresia din Lema 1.

Tangenta la $\mathcal{P}$ într-un punct fixat arbitrar $z(t)$ are ecuaţia

unde $z(t)=a\left(t+\frac{b}{2a}\right)^2+f$, notând cu $f$ valoarea $\frac{-\Delta}{4a}$, iar $z'(t)=2a\left(t+\frac{b}{2a}\right)$.

După Lema 1, proiecţia lui $F(f)$ pe dreapta (7) este

Din ecuaţia axei (6) deducem ecuaţia tangentei în vârful parabolei:

unde $v=\frac{a}{16}\left(\frac{b}{a}-\frac{\overline{b}}{\overline{a}}\right)^2+f$ este vârful lui $\mathcal{P}$, exprimat deja în (5).

Calculând (8), vom vedea că $p(t)$ însumează o parte independentă de $z(t)$, reprezentând un anumit punct fix (diferit însă de $v$) al dreptei (9) şi o parte care are forma $ia\lambda^*$, unde $\lambda^*$ este o anumită valoare (dependentă de $z(t)$) a parametrului $\lambda\in\mathbb{R}$ din (9) – ceea ce va însemna că punctele $p(t)$ sunt situate pe dreapta (9), încheind demonstraţia.

Pentru primul termen din (8) avem imediat: $\frac{z(t)+f}{2}=\frac{a}{2}(t+\frac{b}{2a})^2+f$.

Pentru al doilea termen din (8) avem întâi $\overline{f}-\overline{z(t)}=-\overline{a}(t+\frac{\overline{b}}{2\overline{a}})^2$; rezultă uşor că al doilea termen din (8) are valoarea $-\frac{a}{2}(t+\frac{b}{2a})(t+\frac{\overline{b}}{2\overline{a}})$.

Rezultă $p(t)=\frac{a}{2}(t+\frac{b}{2a})^2+f-\frac{a}{2}(t+\frac{b}{2a})(t+\frac{\overline{b}}{2\overline{a}})$ şi după înmulţiri şi reduceri:

Să observăm întâi că ultimul termen din (10) este de forma $ia\lambda^*$, cu $\lambda^*\in\mathbb{R}$ fiindcă în paranteză avem diferenţa dintre un număr complex şi conjugatul său, ori $z-\overline{z}\in i\mathbb{R}$.

Să arătăm că "partea fixă" din (10), $K=f+\frac{b}{8}\left(\frac{b}{a}-\frac{\overline{b}}{\overline{a}}\right)$ reprezintă un punct al tangentei în vârful parabolei; este suficient să verificăm că dreptele $VF$ şi $VK$ sunt perpendiculare.
Calculând cu atenţia cuvenită găsim că $\frac{f-v}{K-v}=\frac{a\overline{b}-\overline{a}b}{a\overline{b}+\overline{a}b}$, valoare care este "pur imaginară" (din $i\mathbb{R}$) fiindcă numărătorul este de forma $z-\overline{z}\in i\mathbb{R}$, iar numitorul este de forma $z+\overline{z}\in\mathbb{R}$. Rezultă că $VF\perp VK$.

Prin urmare, punctele $p(t)$ date de (8) se exprimă sub forma $p(t)=K+ia\lambda^*$, unde $K$ este un punct (independent de $t$) al tangentei în vârf şi $\lambda^*$ este o valoare reală dependentă de $t$ ("în plus", $ia$ dă direcţia tangentei în vârf); rezultă că $p(t)$ sunt situate pe tangenta în vârful parabolei – altfel spus, proiecţiile punctului $F(\frac{-\Delta}{4a})$ pe tangentele parabolei sunt situate pe tangenta în vârful acesteia, ceea ce înseamnă că acest punct este chiar focarul parabolei.

Concluzii

$\boldsymbol{z(t)=at^2+bt+c},\,t\in\mathbb{R}$ unde $a,b,c\in\mathbb{C}$ sunt afixe de puncte necoliniare, $a\ne 0$ şi $\frac{b}{a}\not\in\mathbb{R}$, reprezintă o parabolă nedegenerată; axa acesteia are direcţia $\arg a$, iar tangenta în punctul de afix $c$ are direcţia $\arg b$.

Afixul focarului este $\boldsymbol{f=\frac{-\Delta}{4a}}$, unde $\Delta=b^2-4ac$.

Diverse elemente ale parabolei se exprimă prin $\boldsymbol{f}$ (fiind reflectate astfel anumite proprietăţi ale focarului), prin $\boldsymbol{z'(t)=2at+b}$ şi prin expresia $\boldsymbol{\delta=\frac{b}{a}-\frac{\overline{b}}{\overline{a}}}$ (care identifică un anumit punct – diferit de origine, fiindcă $\frac{b}{a}\not\in\mathbb{R}$ – de pe axa imaginară):

afixul vârfului parabolei este $\boldsymbol{v=f+\frac{a}{16}\,\delta}$ (şi avem $v=\boldsymbol{z(}-\frac{1}{4}(\frac{b}{a}+\frac{\overline{b}}{\overline{a}})\boldsymbol{)}$).

tangenta în vârf are ecuaţia $\boldsymbol{z=f+\frac{1}{8}\,\delta\,z'(t)},\,t\in\mathbb{R}$; aceasta exprimă, pentru fiecare valoare a parametrului $t$, proiecţia focarului pe tangenta la parabolă în punctul $z(t)$ (însemnând că proiecţiile focarului pe tangente sunt situate pe tangenta în vârf).

directoarea parabolei are ecuaţia $\boldsymbol{z=f+\frac{1}{4}\,\delta\,z'(t)},\,t\in\mathbb{R}$; aceasta exprimă, pentru fiecare valoare a parametrului $t$, simetricul focarului faţă de tangenta la parabolă în punctul $z(t)$ (însemnând că simetricele focarului faţă de tangente sunt situate pe directoarea parabolei).