3. Producerea şi trasarea liniilor (fişierul grafic.eps)

În §2 am descris elipsa asumând că semiaxa mică şi centrul ei sunt transmise prin stivă (vrând să experimentăm şi să lămurim aspecte privitoare la stive, proceduri, variabile şi transformări PS). De fapt, toate elementele necesare programului "grafic.eps" planificat în §1, decurg din descrierea parametrică a punctelor semicardioidei $\mathcal{K}$: $$K(t)=\left(X(t)=2t(2t-1),\,Y(t)=4t\sqrt{t(1-t)}\,\right),\;t\in[0,1]$$

Semiaxa mare a lui $\mathcal{E}$ este $a=1$, semiaxa mică este $b=4t(1-t)$ iar focarele sunt punctele $K(t)$ şi $K(1-t)$. Centrele elipselor $\mathcal{E}$ aparţin arcului de parabolă $\mathcal{P}$ ale cărui puncte sunt date de ecuaţia $y=\sqrt{1-x}$, pentru $x\in[0,1]$.

Corespunzător, în grafic.eps am avea aceste definiţii iniţiale:

%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox: 74 80 320 248

% semicardioida K(t) are ecuaţiile: X(t) = 2t(2t-1), Y(t) = 4tSQRT(t(1-t)); t∈(0,1)
/X {2 mul dup 1 sub mul} bind def  % t este dat în vârful stivei
/Y {dup dup neg 1 add mul sqrt mul 4 mul} bind def

% focarele K(t) şi K(1-t), semiaxa mică, centrul elipsei şi arcele razelor focale 
/tL 0.25 def  % un t între 0 şi 1 (vizând arcul din stânga lui Oy, al lui K(t))
/tR { 1 tL sub } bind def  % 1-t (vizând arcul din dreapta lui Oy, al lui K(t))
/Sb { 4 tL tR mul mul } bind def  % semiaxa mică a elipsei, Sb = 4t(1-t)
/xC { tL X tR X add 2 div } bind def  % mijlocul C(t) pe segmentul K(tL)--K(tR)
/yC { tL Y tR Y add 2 div } bind def  
/arc1 { tL Y tL X atan } bind def  % arcele dintre axa orizontală şi razele focale
/arc2 { tR Y tR X atan } bind def

Am ales pentru $t$ o valoare convenabilă (pentru ca figura finală să fie cât mai clară), tL = 0.25; punctele K(tL) şi K(tR=1-tL) se află pe $\mathcal{K}$ în stânga şi în dreapta axei $Oy$.

y x atan dă $\alpha_1^\circ=\mathrm{arctg}\,\frac{y}{x}$, astfel că 0 0 0.2 arc1 180 arc va produce arcul de cerc cu centrul în originea sistemului curent de coordonate, cu raza 0.2 (faţă de unitatea de măsură aflată în uz în momentul trasării ulterioare, prin stroke), începând în sens antiorar de la unghiul polar $\alpha_1^\circ$ şi încheiat la 180^°. Arcele produse astfel prin arc1 şi arc2 vor marca unghiurile cu $Ox$ ale razelor polare corespunzătoare focarelor lui $\mathcal{E}$ - unghiuri care sunt egale (însemnând că $\mathcal{E}$ este tangentă în $O$ la $Ox$).
Obs. Unghiurile respective fiind egale, era desigur suficient să definim doar arc2 (pentru focarul din dreapta)…

Procedurile introduse mai sus xC, yC şi Sb ne dau, pentru $\mathcal{E}$, coordonatele centrului şi semiaxa mică - încât putem acum înlocui procedura "ellipse" din §2, cu:

% elipsa cu semiaxele a=1 şi Sb, centrată în (xC,yC), tangentă în O la Ox
/Ellipse { gsave  newpath
    /savematrix matrix currentmatrix def % salvează CTM
    xC yC translate  % translatează în centrul elipsei
    Sb sqrt 1 atan rotate  % rotind cu arctg(SQRT(b/a)), devine tangentă în O la Ox
    1 Sb scale  % scalează orizontal cu a şi vertical cu b
    0 0 1 0 360 arc  % "cerc" cu centrul (0,0), "raza" 1 (=a pe Ox şi =b pe Oy)
    savematrix setmatrix  % restaurează CTM ("current transform matrix")
    0.1 setgray
    stroke  % trasează efectiv elipsa
grestore } bind def

De data aceasta, am prevăzut în cadrul procedurii nu numai crearea conturului (ca variabilă de tip "path"), dar şi trasarea efectivă (prin stroke) a elipsei. Bineînţeles că procedând aşa (nu numai descriind linia, dar şi trasând-o apoi), am ambalat conţinutul propriu-zis al procedurii între gsave şi grestore - salvând iniţial şi restaurând în final "contextul grafic" existent în momentul când procedura va fi invocată (conţinând între altele, grosimea liniei de trasare, culoarea acesteia şi matricea CTM, curente).

Producem semicardioida prin puncte cât mai apropiate, unite prin segmente - generând (prin repeat) N=1000 (probabil, am exagerat - dar o să ne intereseze la un moment dat şi cerinţele de memorie) de puncte ale lui $\mathcal{K}$:

% aproximare poligonală (cu N=1000 de segmente) a semicardioidei
/Kardioid { gsave
    /N 1000 def
    /dt 1 N div def  % pasul dt = 0.001
    /t 0 def         % t va parcurge intervalul (0,1), cu pasul dt
    0 0 moveto
    N { /t t dt add def  % t = t+dt
        t X t Y lineto   % segment de la K(t) la K(t+dt)
    } repeat
    1 0 0 setrgbcolor  % roşu
    stroke  % trasează cele 1000 de segmente
grestore } bind def

Vom vedea mai încolo şi o a doua modalitate de a obţine cardioida, folosind curbe Bézier (şi vom încerca să confruntăm rezultatele, vizând memoria necesară în fiecare caz pentru reproducerea curbei, precum şi "calitatea" de redare a acesteia).

Generăm (tot "punct cu punct") şi $\mathcal{P}$, unind punctul curent (iniţializat în vârful parabolei) cu cel corespunzător prin $\sqrt{1-x}$ abscisei depuse pe stivă la iteraţia următoare (prin mecanismul asigurat de for), coborând abscisa cu câte 0.01 dinspre 1 spre 0 (obţinând o aproximare cu 100 de segmente a lui $\mathcal{P}$):

% arcul de parabolă y=SQRT(a(a-x)), x∈[0,a] unde aici, a=1
/Parabola { gsave
    1 0 moveto  % vârful parabolei este punctul (1,0)
    1 -.01 0 {
        dup neg 1 add sqrt lineto
    } for
    0 0 1 setrgbcolor  % albastru
    stroke  % trasează cele 100 de segmente
grestore } bind def

Precizăm că From Step To {Proc} for decurge cam aşa: se depune pe stivă valoarea iniţială From (aici, abscisa 1) şi se execută Proc; apoi valoarea din vârful stivei este "majorată" cu Step (aici cu -0.01, rezultând abscisa utilizată în următoarea iteraţie în Proc) şi dacă astfel nu se "depăşeşte" To, se repetă executarea secvenţei Proc; ş.a.m.d. Pe parcurs, în vârful stivei găsim abscisa $x$ curentă (1, apoi 0.99, 0.98, ..., 0), pe care Proc o poate folosi adăugând-o încă o dată în stivă (prin dup).

Bineînţeles că putem testa grafic.eps în orice moment, adăugând o secvenţă în care mărim convenabil unitatea de măsură, translatăm mai spre centrul paginii, setăm o anumită grosime de trasare şi apoi invocăm procedurile pentru $\mathcal{E}$, $\mathcal{K}$ şi $\mathcal{P}$:

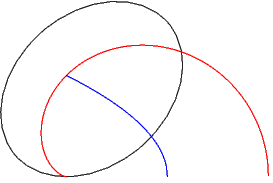
Ne-a rămas de adăugat focarele şi centrul elipsei, segmentele aferente acestora şi cele două arce egale prin care sugerăm că $\mathcal{E}$ este tangentă axei orizontale; ca să evităm "apelarea" separată, constituim o procedură care să conţină toate aceste construcţii:

/other_lines {
    gsave  % triunghiul K(tL) -- K(tR) -- origine
        1 setlinecap
        0.4 setgray
        .003 setlinewidth
        tL X tL Y moveto  % K(t)
        tR X tR Y lineto  % K(1-t)
        0 0 lineto closepath 
        stroke
    grestore
    gsave  % axele Ox, Oy; uneşte vârful parabolei cu centrul elipsei
        2.05 0 -0.3 0 moveto lineto  % Ox (de la abscisa -0.3 până la 2.05)
        0 1.5 0 -0.1 moveto lineto  % Oy (vertical -0.1 .. 1.5)
        1 0 xC yC  moveto lineto  % segmentul C(t)--(1,0)
        0.6 setgray
        0 setlinewidth  % cea mai subţire linie posibilă
        stroke
    grestore
    gsave  % arcele (egale) cu Ox ale razelor focale OK(t) şi OK(1-t)
        newpath
        0 0 0.2 arc1 180 arc
        0 0 0.2 0 arc2 arc
        0.65 setgray  % gri deschis
        0 setlinewidth  % cea mai subţire linie posibilă
        stroke
    grestore
    gsave  % marchează individual punctele K(t), K(1-t) şi C(t)
        newpath
        1 setlinecap  % extinde rotund segmentele, putând marca puncte
        0.02 setlinewidth
        tL X tL Y moveto 0 0 rlineto  % ("segmente" de lungime 0, adică puncte) 
        tR X tR Y moveto 0 0 rlineto
        xC yC moveto 0 0 rlineto 
        0.2 setgray stroke
    grestore
} bind def

Adăugăm în sfârşit ceea ce s-ar numi "programul principal": alegem o unitate de măsură, translatăm sistemul de coordonate astfel încât să "vedem" şi punctele cu abscisă negativă şi setăm în funcţie de unitatea de măsură o anumită grosime a liniei; apoi, invocăm succesiv cele patru proceduri constituite mai sus:

% "programul principal": scalează, poziţionează, alege o grosime şi trasează liniile
90 90 scale  % 90bp = 72bp + 18bp = 1.25 inch (= 4.175 cm)
1.5 1 translate  % originea figurii: 135bp de marginea stângă, 90bp de jos
.005 setlinewidth  % 0.005 din 90bp
Ellipse Kardioid Parabola other_lines

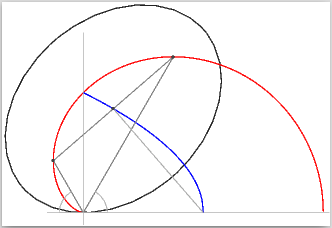
Rămâne să etichetăm focarele, centrul elipsei şi eventual, curbele respective.