6. Eroare, experiment şi descoperire

Situaţiile de "eroare", în pofida aparenţei de "surpriză neplăcută", sunt instructive; provocând chiar, asemenea situaţii şi experimentând în contextul respectiv, poţi ajunge să clarifici aspecte care de obicei sunt vizate expeditiv, ici şi colo.

Dacă în procedura Kardioid din "grafic.eps" (v. §3 în "partea a doua") înlocuim "/N 1000 def" de exemplu, cu "/N 10 def", atunci obţinem un mesaj de eroare:

vb@Home:~/5mai$ gs -q  grafic.eps
Error: /rangecheck in --sqrt--
Operand stack:
   2.0   1.0   -1.19209e-07
Execution stack:
   %interp_exit   .runexec2   --nostringval--   --nostringval-- ... 
...

Chiar neplăcut… pentru 1000 merge, dar pentru 10 nu ?! Dar să profităm de faptul că N este mic (şi să ignorăm deocamdată, mesajul afişat de GS): inserăm nişte instrucţiuni de afişare intermediară a unor valori curente, folosind operatorul " == " (atenţie: spaţiul iniţial şi cel final sunt obligatorii!). În cazul de faţă am insera "t == " în instrucţiunea repetitivă "N {...} repeat" (unde acum N=10):

    N { /t t dt add def  % t = t+dt  (unde dt = 1/N = 0.1)
         t ==  % afişează valoarea t curentă
         t X t Y lineto   % segment de la P(t) la P(t+dt)
    } repeat

şi după aceasta putem vedea cum decurg lucrurile:

vb@Home:~/5mai$ gs -q  grafic.eps
0.1
0.2
0.3
0.4
0.5
0.6
0.700000048  % 0.6 + 0.1 (!)
0.800000072
0.900000095
1.00000012
Error: /rangecheck in --sqrt--
...

Procedura eşuează imediat după ce t ajunge la valoarea 1.00000012, deci la calculul coordonatelor X(t) şi Y(t) ale capătului segmentului curent; ajunge să te uiţi la definiţiile iniţiale, pentru a vedea despre ce este vorba: Y(t) = 4tsqrt(t(1-t)), ori pentru ultima valoare a lui t avem 1-t < 0 - ceea ce determină semnalarea de la începutul mesajului de eroare, pe care acum o putem şi simula direct:

vb@Home:~/5mai$ gs -q 
GS> 1 1.00000012 sub  pstack  sqrt
-1.1920929e-07  % rezultatul scăderii 1 - 1.00000012
Error: /rangecheck in --sqrt--
Operand stack:
   -1.19209e-07
...

Dar altceva este interesant de observat, în experimentul de mai sus: t avea valoarea iniţială 0 şi este incrementat la fiecare iteraţie cu 0.1; însă după 0.6 urmează mai sus 0.700000048 şi nu 0.7! Propagarea acestor erori de aproximare explică faptul că se depăşeşte limita 1, ajungându-se în situaţia de eroare evidenţiată mai sus.

Majoritatea limbajelor de programare (inclusiv PostScript) mizează pe o reprezentare floating point a numerelor reale (o excepţie notabilă este limbajul TeX, creat pe când încă nu apăruse standardul "floating point": pentru a repera cât mai fin "punctele" unei pagini de hârtie, Knuth a introdus reprezentarea numerelor reale ca multipli întregi de $2^{-16}$).
Din cauza erorilor de aproximare inerente, se recomandă ca variabila care asigură iterarea în cadrul unei secvenţe repetitive să fie de tip întreg (nu 0.1, ca mai sus).

Şi în PostScript avem de distins între reprezentarea (şi operarea) internă a numerelor şi pe de altă parte, afişarea acestora - cum arată acest mic experiment:

vb@Home:~/5mai$ gs -q 
GS> /h 0.1 def  % h = 0.1
GS> /g {h 0.6 add} def  % g = h + 0.6
GS> g =
0.7  % valoarea afişată pentru liniştea noastră…
GS> g ==
0.700000048  % valoarea utilizată intern

" = " afişează dacă se poate, cam cum ne-am dori; în schimb " == " (şi încă, " === " pentru anumite alte obiecte PS) produce pe ecran valoarea internă existentă (şi aceasta este cea utilizată în calcule).

7. De la semicardioidă la cardioidă, cu pathforall

Kardioid instituie în memorie conturul poligonal al semicardioidei superioare; vom arăta că prin pathforall putem obţine de aici, conturul întregii cardioide.

Să constituim un fişier cardioid.eps, în care să rescriem deocamdată procedura Kardioid, având grijă de această dată să ghidăm iteraţiile prin întregi:

%!PS
% coordonatele punctelor semicardioidei (t este implicit, în vârful stivei)
/X {2 mul dup 1 sub mul} bind def                    % X(t) = 2t(2t-1)
/Y {dup dup 1 exch sub mul sqrt mul 4 mul} bind def  % Y(t) = 4tSQRT(t(1-t))

/N 1000 def
% aproximare poligonală (cu N segmente) a semicardioidei superioare
/Kardioid {
    0 0 moveto  % conturul pleacă din t=0 (vârful cardioidei)
    1 1 N { N div dup X exch Y lineto } for
} bind def

Să lămurim cum funcţionează 1 1 N { N div dup X exch Y lineto } for (dar ţinem cont că ne-am mai referit la for, în §3 "partea a doua"). La fiecare iteraţie se depune pe stivă valoarea curentă a indexului, i = 1..N; N div adaugă N pe stivă, împarte i la N, elimină cei doi operanzi din stivă şi pune în loc rezultatul i/N; mai departe, dup adaugă a doua oară în stivă i/N, iar X calculează abscisa punctului K(i/N) şi pune rezultatul în locul acestei copii - încât acum stiva conţine vechea valoare i/N şi deasupra acesteia, abscisa rezultată; exch interschimbă între ele aceste două valori, încât apoi, Y poate calcula ordonata lui K(i/N); după aceasta, în stivă avem abscisa şi ordonata punctului K(i/N), iar lineto va adăuga conturului segmentul de la ultimul său punct la K(i/N).

"Conturul" final este constituit din instrucţiunea "0 0 moveto" şi N=1000 de instrucţiuni lineto pentru segmentele care unesc K((i-1)/N) cu K(i/N), unde i=1..N. Putem "vedea" conturul (adică, instrucţiunile constituente), folosind operatorul pathforall; trebuie să-i transmitem pe stivă patru proceduri, vizând respectiv instrucţiunile moveto, lineto, curveto şi closepath din componenţa conturului curent; în fiecare caz, sunt plasate pe stivă coordonatele punctelor angajate în instrucţiune şi apoi se execută procedura transmisă pentru acel tip de instrucţiune.

De exemplu, dacă după ce am constituit un contur, am invoca { = = } {} {} {} pathforall, atunci s-ar afişa coordonatele din toate instrucţiunile moveto ale conturului respectiv (şi numai acestea, fiindcă celelalte trei proceduri transmise sunt vide): pentru fiecare instrucţiune x y moveto existentă în conturul curent, pathforall va pune în stivă x y şi va executa procedura indicată { = = }, ceea ce extrage pe rând cele două valori din stivă şi le afişează una sub alta (" = " este suficient pentru aceasta, dar mai bine este să folosim " == " - cum am arătat la §6).
Afişarea "una sub alta" a valorilor este foarte convenabilă dacă intenţionăm să le preluăm ulterior într-un alt program (indiferent în ce limbaj), pentru anumite prelucrări independente; dar putem să le afişăm şi într-un format mai "convenabil", înlocuind "{ = = }" cu {[3 1 roll] == }: se adaugă în stivă obiectul (de tip "array") [...], încât acum stiva conţine x y [3 1 roll]; apoi se execută instrucţiunea din interior 3 1 roll, prin care conţinutul stivei este rotit spre dreapta şi este înlocuit cu un singur "array", anume [x y] (pentru a cărui afişare este acum necesar " == "). Putem verifica direct, în GS: de exemplu, GS> 7.2 5.6 [3 1 roll] == produce GS<1> [7.2 5.6].

Însă pathforall poate fi utilizat şi în scopuri mai interesante decât simpla afişare de valori - anume, pentru modificarea sau extinderea conturului curent. Să adăugăm în fişierul cardioid.eps o secvenţă prin care prevedem o unitate de măsură şi o grosime de linie convenabile, mutăm originea undeva mai la mijlocul paginii şi apoi, invocăm procedura Kardioid, obţinând conturul semicardioidei superioare; invocând pathforall cu o procedură pentru instrucţiunile x y lineto în care schimbăm semnul ordonatelor (folosind neg), conturului curent îi vor fi adăugate noile instrucţiuni x -y lineto - încât în final, conturul va conţine segmentele iniţiale ale semicardioidei superioare, dar şi pe cele "simetrice" acestora faţă de $Ox$. În final, afişăm conturul astfel "întregit", folosind din nou pathforall:

90 90 scale  % 90bp = 72bp + 18bp = 1.25 inch (= 4.175 cm)
1.5 5 translate  % originea figurii: 135bp de marginea stângă, 450bp de jos
.005 setlinewidth  % 0.005 din 90bp

Kardioid  % constituie conturul poligonal al semicardioidei superioare

% adaugă "aceleaşi" segmente, dar schimbând semnul ordonatelor
{moveto} {[3 1 roll neg lineto]} {} {}  
    pathforall  % rezultă conturul întregii cardioide

% afişează instrucţiunile conturului curent (după "întregire")
{[3 1 roll] == }  % [x y] din instrucţiunile 'moveto' ale conturului
{[3 1 roll (lineto)] == }  % [x y lineto]
{} {}
    pathforall

clear  % curăţă stiva (cum-necum, au rămas 4 tablouri vide...)
stroke  % trasează efectiv cardioida (nu numai semicardioida!)

Pentru exemplu, să redefinim /N 4 def şi să lansăm programul sub GS:

vb@Home:~/5mai$ gs -q  cardioid.eps
[2.53962298e-05 1.61245898e-05]  % moveto
[-0.250021845 0.433032304 (lineto)]
[2.53962298e-05 0.999998689 (lineto)]
[0.750012338 1.29901314 (lineto)]
[1.99999058 1.61245898e-05 (lineto)]
[2.53962298e-05 1.61245898e-05]    % moveto
[-0.250021845 -0.433051646 (lineto)]
[2.53962298e-05 -1.000018 (lineto)]
[0.750012338 -1.29903245 (lineto)]
[1.99999058 -3.54741e-05 (lineto)]
GS>

Se vede că au rezultat nu numai cele 4 segmente care "aproximează" semicardioida superioară, dar şi simetricele acestora faţă de $Ox$; de observat însă, că neg nu a schimbat pur şi simplu semnele, ci a şi evaluat cumva, rezultând obişnuitele "erori de aproximare" (astfel, 0.433032304 a ajuns -0.433051646 ceea ce diferă de valoarea corectă -0.433032304, cu vreo două sutimi de miime). În orice caz, pentru N=4 şi respectiv N=1000 obţinem imaginile următoare:

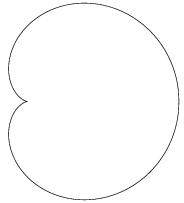
Subliniem că trasarea conturului pentru N=1000 necesită execuţia a 2002 instrucţiuni (două moveto şi 1000 + 1000 instrucţiuni lineto); vom arăta acuşi că putem trasa cardioida (şi alte curbe) cam cu aceeaşi acurateţe (totuşi… arătând mai bine!), dar cu un contur conţinând mult mai puţine instrucţiuni (anume, instrucţiuni curveto). Am avansa ideea cam aşa: dacă în loc de cele 4 segmente din prima figură am considera nişte arce curbate cumva "din ochi", sau din ecuaţiile curbei iniţiale, atunci conturul constituit de acestea ar fi oricum "mai bun", decât cel poligonal iniţial.