13. Aproximarea prin cubice Bézier a unei curbe oarecare

Am ilustrat mai înainte faptul că PostScript conturează literele folosind secvenţe de instrucţiuni curveto; în treacăt fie zis - şi noi facem la fel în clasa întâia: desenăm literele cu "bastonaşe" şi arce de legătură (angajând intuitiv şi anumite "puncte de control"). Să vedem şi cum am putea folosi cubice Bézier pentru a contura o curbă sau alta, plecând de la ecuaţiile acesteia; subliniem că nu graficul ca atare, ne interesează (că atunci, l-am obţine fără bătaie de cap folosind R, sau vreun alt pachet de grafică); vrem să vedem cum ajungem la un program care să ne contureze curba respectivă, cât se poate de exact şi cu cât mai puţine instrucţiuni curveto.

Pentru cubica Bézier de capete $P$, $Q$ şi cu punctele de control $F\equiv(2\mathsf{H}+\mathsf{P})/3$ şi $G\equiv(2\mathsf{H}+\mathsf{Q})/3$ - unde $H$ era intersecţia tangentelor în capete - ajunsesem la exprimarea (literele drepte desemnând afixele punctelor omonime, în $\mathbb{C}\,$): $$z(t)=(1-t)^3\,\mathsf{P}+3(1-t)^2t\,\mathsf{F}+3(1-t)t^2\,\mathsf{G}+t^3\,\mathsf{Q},\,t\in[0,1]\quad\quad\quad(1)$$

Conturul asociat se obţine fixând "punctul curent" în $P$ şi indicând operatorului curveto coordonatele punctelor $F$, $G$ şi $Q$. Însă determinarea punctelor $F$ şi $G$ plecând de la intersecţia $H$ a tangentelor în capete este incomodă.

Putem ocoli determinarea prealabilă a lui $H$, exprimând coeficienţii $\mathsf{F}$ şi $\mathsf{G}$ chiar din ecuaţia lui $z(t)$: derivând, găsim $z'(0)=-3\mathsf{P}+3\mathsf{F}$ şi $z'(1)=-3\mathsf{G}+3\mathsf{Q}$; deci $$\mathsf{F}=\mathsf{P}+\frac{1}{3}z'(0),\quad \mathsf{G}=\mathsf{Q}-\frac{1}{3}z'(1)\quad\quad\quad(2)$$

$z'(0)$ şi $z'(1)$ sunt pantele tangentelor curbei în capetele $P$ şi $Q$ (fiindcă avem $z(0)=\mathsf{P}$ şi $z(1)=\mathsf{Q}$). Pentru unele "cazuri speciale" trebuie totuşi să angajăm $H$; de exemplu, dacă $z'(1)=\infty$ şi $z'(0)\ne\infty$ atunci determinăm întâi intersecţia $H$ a tangentei în $P$ cu verticala prin $Q$ şi apoi căutăm cumva $G$ pe segmentul $QH$ ("teoretic", adică ignorând complet erorile de aproximare, avem $QG=\frac{2}{3}QH$).

Pentru a aproxima conturul unei curbe oarecare $\mathcal{K}$ (dată fiind, într-o formă sau alta, ecuaţia acesteia) putem proceda astfel: partiţionăm $\mathcal{K}$ în câteva părţi, având fiecare câte un capăt iniţial $P$ şi unul final $Q$; determinăm valorile în $P$ şi $Q$ ale derivatei funcţiei asociate lui $\mathcal{K}$ şi găsim prin formulele (2) coeficienţii $\mathsf{F}$ şi $\mathsf{G}$; "identificăm" arcul lui $\mathcal{K}$ delimitat de $P$ şi $Q$ prin cubica Bézier dată de $\mathsf{P}$, $\mathsf{F}$, $\mathsf{G}$ şi $\mathsf{Q}$.

Desigur, "găsim $\mathsf{F}$ şi $\mathsf{G}$ prin formulele (2) " trebuie regândit, fiindcă $P$ şi $Q$ de pe curba $\mathcal{K}$ se obţin din ecuaţia acesteia nu pentru $t=0$ şi $t=1$, ci eventual pentru $t=\tau_0$ şi $t=\tau_1$ - indicând subintervalul parcurs de parametrul în funcţie de care se obţine porţiunea lui $\mathcal{K}$ de capete $P$ şi $Q$.

Schimbarea de variabilă $t=\dfrac{\tau\,-\,\tau_0}{\tau_1\,-\,\tau_0}$ transformă biunivoc $t\in[0,1]$ în $\tau\in[\tau_0,\tau_1]$. Pentru (2) nu interesează ce devine (1) prin această substituţie, ci doar cum se transformă $z'(t)$ trecând la noua variabilă $\tau$; plecând de la regula de "derivare înlănţuită", avem: $\frac{\mathrm{d}z}{\mathrm{d}t}=\frac{\mathrm{d}z}{\mathrm{d}\tau}\,\frac{\mathrm{d}\tau}{\mathrm{d}t} = (\tau_1\,-\,\tau_0)\frac{\mathrm{d}z}{\mathrm{d}\tau}$. Aceasta înseamnă că în loc de $z'(t)$ trebuie să punem $h\,z'(\tau)$, notând $h=\tau_1\,-\,\tau_0$; deci formulele (2) se adaptează la intervalul $[\tau_0,\,\tau_1]$ astfel: $$\mathsf{F}=\mathsf{P}+\frac{h}{3}z'(\tau_0),\quad \mathsf{G}=\mathsf{Q}-\frac{h}{3}z'(\tau_1),\,\text{unde }h=\tau_1\,-\,\tau_0\quad\quad\quad(3)$$

Conturul lui $\mathcal{K}$ va fi constituit dintr-un număr de instrucţiuni curveto egal cu numărul părţilor considerate; pentru a creşte calitatea "identificării" cu arce Bézier, trebuie să folosim o partiţionare a lui $\mathcal{K}$ cu un număr suficient de mare de părţi (având în vedere eventual şi anumite "puncte speciale", cum ar fi vârfurile şi punctele de inflexiune).

14. Exemplu: aproximarea cardioidei prin cubice Bézier

Reluăm din §8 procedura Kardioid, prin care conturul semicardioidei superioare $\mathscr{K}$ (pe care acum, îl vom "umple" folosind fill) este constituit prin 1000 de instrucţiuni lineto (producând cu siguranţă, un grafic suficient de exact):

%!PS-Adobe-2.0 EPSF-2.0
% coordonatele punctelor semicardioidei K(t) (t este implicit, în vârful stivei)
/X {2 mul dup 1 sub mul} bind def                    % X(t) = 2t(2t-1)
/Y {dup dup 1 exch sub mul sqrt mul 4 mul} bind def  % Y(t) = 4tSQRT(t(1-t))

/N 1000 def  % aproximare poligonală (cu N segmente) a semicardioidei superioare
/Kardioid {
    0 0 moveto  % conturul pleacă din K(0) (nodul cardioidei)
    1 1 N { N div dup X exch Y lineto } for  % segmente K(t)---K(t+1/N), t=i/N, i=0..N
} bind def

108 108 scale  2 1 translate
Kardioid  % instanţiază semicardioida (pentru noul sistem de coordonate)
.5 setgray  fill  % "închide" şi umple conturul cu pixeli gri

Dăm întâi un mic exemplu de constituire manuală (calculând direct, după formulele (3)), a unor instrucţiuni curveto care să "acopere" cumva, semicardioida umplută cu gri obţinută prin programul de mai sus (vezi conturul roşu pe figura de mai jos).

Cel mai simplu (pentru calcul manual - altfel, vom vedea că nu este deloc bine) ar fi să partiţionăm în două bucăţi: arcul descris pentru $t\in[0,\frac{1}{2}]$, având capetele $O(0,0)$ (nodul cardioidei) şi $B(0,1)$, respectiv pentru $t\in[\frac{1}{2},1]$ de capete $B(0,1)$ şi $A(2,0)$ (vârful cardioidei). Urmează să calculăm pentru fiecare arc, punctele $F$ şi $G$ din (3).

Amintim că punctele lui $\mathscr{K}$ sunt date de $$x(t)=2t(2t-1),\;y(t)=4t\sqrt{t(1-t)},\;t\in[0,1]$$ şi găsim uşor $$x'(t)=2(4t-1),\;y'(t)=2(3-4t)\sqrt{\frac{t}{1-t}}\quad(t\ne 1; y'(1)=\infty)$$

Pentru capătul $O$, avem: $z'_O=(x'(t), y'(t))|_{t=0}=(-2,0)$ deci după (3), cu $h=\frac{1}{2}$, avem $\mathsf{F}=\mathsf{O}+\frac{h}{3}z'_O=(-\frac{1}{3},0)$.
Pentru capătul $B$, avem: $z'_B=(x'(t), y'(t))|_{t=0.5}=(2,2)$ şi după (3) rezultă $\mathsf{G}=\mathsf{B}-\frac{h}{3}z'_B=(0,1)-\frac{1}{6}(2,2)=(-\frac{1}{3},\frac{2}{3})$.

Prin urmare, cubica Bézier asociată primului arc va fi dată de O(0,0) F(-1/3,0) G(-1/3,2/3) B(0,1) curveto, ceea ce adăugăm în programul de mai sus astfel:

0 0 moveto  -1 3 div 0 -1 3 div 2 3 div 0 1 curveto

Pentru arcul lui $\mathscr{K}$ dintre $B$ şi $A$ putem determina $\mathsf{F}=\mathsf{B}+\frac{h}{3}z'_B=(\frac{1}{3},\frac{4}{3})$, dar $\mathsf{G}$ nu mai poate fi obţinut prin (3) fiindcă $y'_A=y'(1)=\infty$; am dat de o dilemă tipică faţă de aplicarea formulelor (3) - cazul în care tangenta la curbă într-un capăt al arcului este verticală. Soluţia ad-hoc (dar nici nu ştim alta) ar consta în a alege $G$ undeva pe tangenta în $A$, deci $G(2, \lambda)$; luăm $\lambda=2$ şi adăugăm în program:

1 3 div 4 3 div  2 2  2 0  curveto
0 0 1 setrgbcolor  stroke  % cele două cubice sunt trasate cu roşu

Pentru comparaţie, am repetat ultima instrucţiune curveto pentru cazurile $\lambda\in\{2-\frac{1}{3},2-\frac{2}{3}, 1\}$, colorând acum cu albastru:

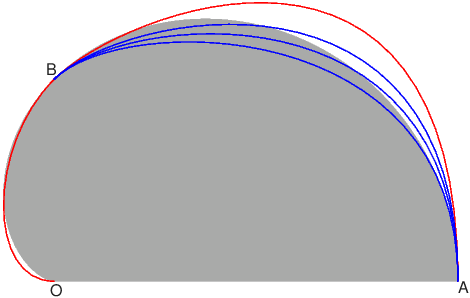
Contururile rezultate astfel (cel format din două arce roşu-roşu, sau cele constituite din arcul roşu şi unul dintre cele albastre) sunt departe de o aproximare acceptabilă a semicardioidei şi chiar este greu de crezut că separând în numai două arce am putea obţine una acceptabilă.

Să ştergem instrucţiunile curveto calculate manual mai sus şi să adoptăm acum ideea cea mai simplă: împărţim intervalul $[0,1]$ în N bucăţi egale (cel puţin patru) şi pentru fiecare dintre acestea determinăm punctele de control necesare instrucţiunii curveto pentru aproximarea porţiunii corespunzătoare a lui $\mathscr{K}$. Vom scrie programul necesar pentru aceasta fără cine ştie ce elaborare, doar ca să vedem cam "cum s-ar face"; dar oricum am elabora, acest program va fi mult mai amplu (şi mai complicat) decât procedura iniţială Kardioid (care practic are o singură linie de program). Ce "deranja" la Kardioid era faptul că producea 1000 de instrucţiuni lineto; acum vom produce $\mathscr{K}$ într-o aproximare acceptabilă (dar nu aşa de bună ca folosind Kardioid) cu numai N=6 instrucţiuni curveto (sau mai bine, N=9 şi mai bine, N=12; cu flattenpath şi pathforall se va putea vedea că acestea acoperă maximum 50-60 de instrucţiuni lineto).

Introducem întâi procedurile dX şi dY, pentru a calcula $x'(t)$ şi $y'(t)$ (valoarea $t$ fiind preluată de pe stiva operanzilor); apoi fixăm N (a încerca valorile 2..6..9; pentru N=10 sau N=11 programul eşuează, în urma propagării unor erori "de aproximare" - cum am mai observat în §6; pentru N=12 iarăşi "merge"). Introducem variabilele h=1/N şi h3=h/3, fiindcă aceste valori vor interveni frecvent în calcule; apoi iniţializăm t0, fixăm punctul curent în $O(0,0)$ şi repetăm de N ori secvenţa de instrucţiuni care plecând de la capătul P≡(x(t0), y(t0)), determină Q≡(x(t1), y(t1)) cu t1 = t0 + h şi apoi calculează după formulele (3) punctele de control F şi G - producând instrucţiunea curveto pentru P, F, G şi Q.
Am întâmpinat faptul că $y'(1)=\infty$ folosind ifelse: când t1 ≥ 0.99, intersectăm tangenta în P cu verticala x=2 (tangenta în vârful cardioidei) găsind $H$ la ordonata $y_H=y(t_0)+\frac{y'(t_0)}{x'(t_0)}(2-x(t_0))$; punctul $G$ are abscisa 2 şi ar trebui să aibă ordonata $\frac{2}{3}y_H$ - dar (cred că din cauza cumulării erorilor de aproximare) a trebuit să experimentez pentru a apropia mai mult cubica respectivă de cardioidă, mărind puţin ordonata lui $G$ până la valoarea $\frac{2.6}{3}y_H$ (optând în final pentru 2.58/3):

/dX {8 mul 2 sub} bind def  % X'(t) = 8t - 2
/dY {/t exch def  % t ==  %% (vedem eventual, "erorile de aproximare")
     6 8 t mul sub t 1 t sub div sqrt mul 
} bind def  % Y'(t) = 2(3-4t)SQRT(t/(1-t))

/N 9 def 
/h 1 N div def  % 1/N
/h3 h 3 div def  % h/3
/t0 0 def  t0 X t0 Y  moveto
N {
    /t1 t0 h add def  % t1 = t0 + h  (t0 referă capătul iniţial al arcului curent)
    t0 X h3 t0 dX mul add  % F (primul punct de control)
    t0 Y h3 t0 dY mul add
    t1 0.99 ge  % la t1==1 avem tangentă verticală şi trebuie găsit H
   { 2 t0 Y  t0 dY t0 dX div  2 t0 X sub  mul  add 
     2.58 3 div  mul }  % G este pe segmentul QH, încât QG/GH ≈ 2/3
   { t1 X h3 t1 dX mul sub  % G (al doilea punct de control) dacă t1 < 0.99
    t1 Y h3 t1 dY mul sub } ifelse
    t1 X t1 Y  % Q (capătul final pentru arcul curent)
    curveto
    /t0 t1 def  % t0 = t1
} repeat
1 0 0 setrgbcolor  0.005 setlinewidth  stroke

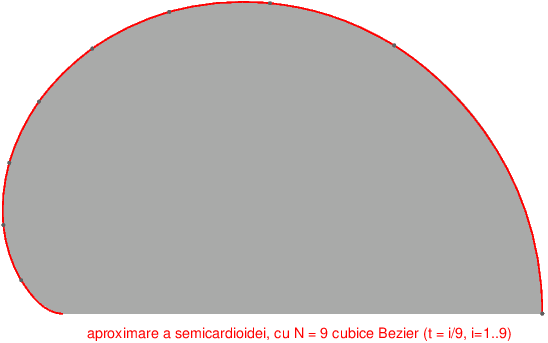
Am marcat şi punctele semicardioidei care sunt capetele finale ale celor 9 cubice Bézier determinate prin secvenţa de mai sus, adăugând în final:

/t0 0 def
0.3 setgray
N { /t1 t0 h add def  % t1 = i/N, i=1..N
    t1 X t1 Y moveto
    t1 X t1 Y .007 0 360 arc fill  % marchează punctul (x(t1), y(t1))
    /t0 t1 def
} repeat

Nu m-am mai străduit să verific vreo altă modalitate de partiţionare; de exemplu, ar fi de bănuit că un sistem de valori $t\in[0,1]$ mai dese spre capetele t=0 şi t=1 (mai ales spre t=1) şi mai rare în mijloc ar putea duce la cubice Bézier (tot vreo 10, probabil) mai "fidele" cardioidei.

În urma experienţei de lucru descrise mai sus devine clar cred, că mai totdeauna este de preferat un program simplu, modelând aproximarea poligonală obişnuită (fie şi cu 1000 de lineto, generate desigur printr-o instrucţiune repetitivă), unuia care constituie şi înlănţuie cubice Bézier care să aproximeze porţiuni ale curbei (mai ales dacă vrem o reprezentare cât mai exactă). curveto a fost introdusă nu pentru a trasa curbe pe baza ecuaţiilor acestora, ci mai degrabă pentru a permite realizarea interactivă de figuri (sau caractere) prin intermediul unor aplicaţii ca Adobe Illustrator, sau CorelDraw, Inkscape, etc.