9. Arcele de parabolă sunt curbe Bézier pătratice

În procedura Parabola din §3, am generat "punct cu punct" arcul de parabolă $\mathcal{P}$ dat de $y=\sqrt{1-x},\,x\in[0,1]$: se unea punctul curent (iniţializat în vârful parabolei) cu cel corespunzător abscisei depuse pe stivă la iteraţia următoare (prin mecanismul lui for), coborând abscisa cu câte 0.01; în final avem o aproximare cu 100 de segmente a lui $\mathcal{P}$ – în fond, un set de 100 de instrucţiuni lineto care prin operatorul stroke vor produce pixeli vecini sau puncte suficient de apropiate, formând (pe ecran, sau pe hârtie) o imagine grafică acceptabilă a lui $\mathcal{P}$.
Obs. Iterarea cu paşi fracţionari este însă, nerecomandată - vezi §6.

Vom arăta mai încolo că putem obţine o imagine la fel de bună a lui $\mathcal{P}$ (şi de fapt, a oricărui arc de parabolă), folosind o singură instrucţiune curveto (în loc de 100 lineto); dar pentru aceasta trebuie găsite în prealabil, anumite "puncte de control".

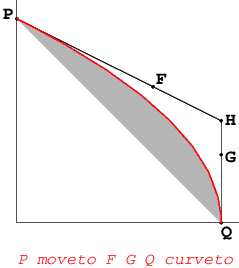
Să notăm cu $P$ şi $Q$ capetele arcului $\mathcal{P}$ (în cazul nostru $P(0,1)$ şi $Q(1,0)$); urmează să determinăm "punctele de control".

Fie $H$ intersecţia tangentelor în $P$ şi $Q$, la $\mathcal{P}$. Justificarea alegerii în acest fel a unui prim punct de control decurge dintr-o metodă generală de construcţie punctuală a unei conice (v. Steiner's generation of a conic), care în cazul nostru revine la această proprietate: dacă punctele $U$ şi $V$ împart segmentele orientate $\overline{PH}$ şi $\overline{HQ}$ într-un acelaşi raport $t\in[0,1]$, atunci punctul care împarte $\overline{UV}$ în raportul $t$ descrie (când $t$ variază de la 0 la 1) un arc de parabolă, care este tangent dreptelor $PH$ şi $QH$.

Pentru demonstraţie, să considerăm afixele punctelor, folosind litere omonime. Punctul care împarte $\overline{UV}$ în raportul $t$ este $z(t)=(1-t)\mathsf{U}+t\mathsf{V}$; dar - fiindcă $U$ împarte $\overline{PH}$ în raportul $t$ - avem $\small u=(1-t)\mathsf{P}+t\mathsf{H}$; analog, $\small v=(1-t)\mathsf{H}+t\mathsf{Q}$. Rezultă: $$z(t)=(1-t)^2\mathsf{P}+2t(1-t)\mathsf{H}+t^2\mathsf{Q},\,t\in[0,1]$$ Deci (fiind date de o funcţie de gradul doi în $t$) punctele $z(t)$ se află pe o parabolă care trece prin $z(0)=\mathsf{P}$ şi $z(1)=\mathsf{Q}$.
Avem $z'(t)=-2(1-t)\mathsf{P}+2(1-2t)\mathsf{H}+2t\mathsf{Q}$; rezultă că $z'(0)=2(\mathsf{H}-\mathsf{P})$ (adică tangenta în $z(0)$ are aceeaşi direcţie ca vectorul $\overline{PH}$) şi $z'(1)=2(\mathsf{Q}-\mathsf{H})$; deci dreptele $PH$ şi $HQ$ sunt tangente parabolei, în $P$ şi respectiv în $Q$.

Arcul de parabolă $z(t)$ rezultat mai sus este curba Bézier pătratică definită de capetele $P$, $Q$ şi de punctul de control $H$; dacă am avea o instrucţiune (similară cu lineto) care să furnizeze această curbă Bézier (primind ca argument capetele şi punctul de control), atunci am putea trasa $\mathcal{P}$ folosind numai această instrucţiune. Însă pentru a viza şi alte curbe (nu numai parabola), PostScript prevede implicit folosirea curbelor Bézier cubice, care necesită câte două puncte de control; vom vedea mai jos că pentru cazul unui arc de parabolă, acestea pot fi determinate plecând de la punctul $H$ definit mai sus.

Să verificăm într-un caz concret, că pătratica Bézier definită de capetele unui arc de parabolă şi de intersecţia tangentelor acestuia în capete coincide cu arcul respectiv.
Pentru cazul nostru $\mathcal{P}:\,y^2=1-x,\,x\in[0,1]$ şi prin derivare avem $2yy'=-1$; deci $y'(0)=-\frac{1}{2y(0)}=-\frac{1}{2}$, încât ecuaţia tangentei în $P(0,1)$ este $y-1=-\frac{1}{2}x$; tangenta în $Q(1,0)$ este $x=1$. Rezultă prin intersecţie $H(1,\frac{1}{2})$ şi curba Bézier pătratică asociată mai sus este $z(t)=(1-t)^2i+2t(1-t)(1+\frac{1}{2}i)+t^2$, adică separând părţile (reală şi imaginară): $x(t)=2t(1-t)+t^2=t(2-t)$ şi $y(t)=(1-t)^2+t(1-t)=1-t$; eliminând parametrul $t$ rezultă exact ecuaţia iniţială, $y^2=1-x$.

10. Aproximarea arcelor de parabolă prin cubice Bézier

Am văzut mai sus că ecuaţia arcului de parabolă de capete $P$ şi $Q$, dat fiind punctul ("de control") $H$ în care se intersectează tangentele în capete este (în planul complex) $z(t)=(1-t)^2\mathsf{P}+2(1-t)t\mathsf{H}+t^2\mathsf{Q},\,t\in[0,1]$. Avem de găsit două puncte $F$ şi $G$ cu aceeaşi proprietate ca $H$ - adică $FP$ şi $GQ$ să fie tangente parabolei; deci $F$ şi $G$ trebuie căutate pe dreptele $HP$ şi $HQ$.

Pe de altă parte, vrem un polinom de gradul trei care să "reprezinte" cumva, arcul de parabolă $z(t)$; cubica respectivă ar trece prin capetele $P$ şi $Q$ (pentru $t=0$ şi $t=1$) dacă polinomul ar conţine monoamele $(1-t)^3\mathsf{P}$ şi $t^3\mathsf{Q}$, iar celelalte două monoame ar conţine $t(1-t)$ (încât ele să nu afecteze valorile în capetele $t\in\{0,1\}$). Observând că $(1-t)+t=1$, putem satisface aceste cerinţe înmulţind $z(t)$ cu $(1-t)$ şi respectiv cu $t$ şi adunând apoi rezultatele; rezultă astfel această rescriere: $$z(t)=(1-t)^3\mathsf{P}+(1-t)^2t(2\mathsf{H}+\mathsf{P})+(1-t)t^2(2\mathsf{H}+\mathsf{Q})+t^3\mathsf{Q}$$ Punctele de control căutate $F$ şi $G$ ar fi reprezentate de cei doi coeficienţi din mijloc, dar nu direct - fiindcă (de exemplu, pentru primul coeficient) punctul de afix $2\mathsf{H}+\mathsf{P}$ este exterior dreptei $HP$ (originea planului fiind fixată arbitrar). Pentru ca $F$ să se afle "la momentul" $t$ pe segmentul orientat $\overline{PH}$ şi în acelaşi timp, să se afle pe raza polară a punctului $2\mathsf{H}+\mathsf{P}$ trebuie îndeplinită pentru un anumit factor $\lambda$, condiţia: $(1-t)\mathsf{P}+t\mathsf{H}=\lambda(2\mathsf{H}+\mathsf{P})$ din care deducem $2\lambda=t$ şi $\lambda=1-t$, care adunate, ne dau $\lambda=\frac{1}{3}$. Prin urmare $F=\frac{1}{3}(2\mathsf{H}+\mathsf{P})$; pentru celălalt coeficient este suficient să schimbăm $\mathsf{P}$ cu $\mathsf{Q}$ (dar putem şi repeta analog, calculul) şi avem $G=\frac{1}{3}(2\mathsf{H}+\mathsf{Q})$.

Pentru a evita factorul $\frac{1}{3}$, putem amplifica monoamele din mijloc cu $3$, obţinând o expresie mai obişnuită a cubicei Bézier: $$z(t)=(1-t)^3\,\mathsf{P}+3(1-t)^2t\,\mathsf{F}+3(1-t)t^2\,\mathsf{G}+t^3\,\mathsf{Q},\,t\in[0,1]$$ asociate capetelor unui arc de curbă date de coeficienţii extremi şi punctelor de control date de coeficienţii din mijloc.

11. Instrucţiunea curveto

Cubicele Bézier sunt modelate în PostScript prin operatorul curveto: acesta presupune că punctul curent (stabilit de exemplu printr-o instrucţiune moveto) este capătul de start al arcului şi cere de pe stivă coordonatele punctelor de control şi pe cele ale capătului final. De exemplu, pentru arcul de parabolă $\mathcal{P}$ avem din §9 $P(0,1)$, $Q(1,0)$ şi $H(1, 0.5)$ iar după §10 găsim $\mathsf{F}=\frac{1}{3}(2\mathsf{H}+\mathsf{P})=(\frac{2}{3},\frac{2}{3})$ şi $\mathsf{G}=(1,\frac{1}{3})$; deci pentru a obţine $\mathcal{P}$ sunt suficiente aceste două instrucţiuni: 0 1 moveto (care stabileşte $\mathsf{P}$ ca punct curent) şi apoi 0.66 0.66 1 0.33 1 0 curveto; desigur că n-am introduce "0.66 0.66", ci am prefera "2 3 div dup".

În programul următor, redefinim faţă de §3 'Parabola' (folosind aceeaşi metodă ca la definiţia 'Kardioid' din §7); aceasta produce un contur poligonal pentru $\mathcal{P}$ cu N=100 segmente (instrucţiuni lineto). Adăugăm apoi o procedură care produce $\mathcal{P}$ cu o singură instrucţiune curveto; dar ne convingem, folosind pathforall (vezi §7) şi flattenpath că de fapt, această instrucţiune acoperă la execuţie (prin stroke) un anumit număr (dar mic, comparând cu N=100) de instrucţiuni lineto.

%!PS-Adobe-2.0 EPSF-2.0
/N 100 def
/Parabola {  % prin N segmente
    0 1 moveto
    0 1 N {N div dup 1 exch sub sqrt lineto} for  % i/N  SQRT(1-i/N)
} bind def

/Parabola3 { % drept cubică Bézier (o instrucţiune 'curveto')
    0 1 moveto
    2 3 div dup 1 1 3 div 1 0 curveto
} bind def

108 108 scale  1 2 translate  .004 setlinewidth

gsave  .65 setgray
    Parabola fill  % "umple" conturul poligonal (de N segmente)
grestore

gsave  1 0 0 setrgbcolor
    Parabola3  % prin 'curveto'
    {[3 1 roll] == } {} {[7 1 roll (curveto)] == } {} pathforall
    (\n) print
    flattenpath  % înlocuieşte 'curveto' prin secvenţe 'lineto' echivalente
    {[3 1 roll] == } {[3 1 roll (lineto)] == } {} {} pathforall
    stroke  % intern, 'stroke' va aplica "flattenpath"
grestore 

stroke (care controlează, în final, trasarea efectivă, pe ecran sau pe hârtie) înlocuieşte automat conturul indicat într-o instrucţiune curveto printr-un contur ("echivalent" cubicei Bézier iniţiale) constituit din instrucţiuni lineto - probabil chiar acelea pe care le-am cerut prin pathforall (după ce am liniarizat direct, invocând flattenpath) şi pe care le putem vedea executând programul prin GS:

vb@Home:~/5mai$ gs -q  par_bez.eps 
[-1.73843237e-05 0.999990702]  % 0 1 moveto
[0.666680694 0.66666311 1.00000823 0.333335608 1.00000823 8.06229491e-06 (curveto)]
% flattenpath transformă conturul într-o secvenţă (echivalentă) de lineto:
[-1.73843237e-05 0.999990702]
[0.0593211092 0.970321417 (lineto)]
[0.234326661 0.874992847 (lineto)]
[0.437496513 0.749995053 (lineto)]
[0.609363139 0.624997199 (lineto)]
[0.749969602 0.499999374 (lineto)]
[0.859358788 0.37500155 (lineto)]
[0.937487841 0.250003725 (lineto)]
[0.984356642 0.125005886 (lineto)]
[1.00000823 0.0312682688 (lineto)]
[1.00000823 8.06229491e-06 (lineto)]
>>showpage, press <return> to continue<<

Dacă decupăm secvenţa celor 10 instrucţiuni 'lineto' afişate şi o încorporăm (eliminând desigur, parantezele) la sfârşitul programului, putem constata că rezultă (suprapus) acelaşi contur ca şi cel produs de 'Parabola' şi de 'Parabola3'.

Este interesant de comparat: noi am generat segmentele (prin for) folosind (ceea ce este absolut uzual) un pas constant (aici, 0.01), fără a distinge în vreun fel punctele curbei; în schimb, flattenpath (sau stroke) - atunci când liniarizează conturul indicat în curveto - distinge cumva (ceea ce este desigur, mai inteligent), între părţile mai întinse şi cele mai bombate ale arcului, parcurgându-le cu paşi ceva mai mari, respectiv ceva mai mici (a vedea diferenţele absciselor la primele şi respectiv la ultimele instrucţiuni 'lineto' dintre cele redate mai sus în [...]).

Pare deci mai bine (până la vreo probă contrarie) să calculăm punctele de control necesare şi să folosim curveto, decât să iterăm lineto pe 100 de paşi echidistanţi (şi de obicei, mai mulţi), trasând câte un segment de la punctul curent la cel următor; în cazul unei curbe mai "largi" sau mai complicate (un exemplu ar fi şi conturul vreunei litere, într-un anumit font), ne putem gândi să o segmentăm întâi în câteva bucăţi şi să folosim curveto pentru fiecare dintre acestea.

12. Raţiunea de a fi a instrucţiunii curveto

lineto şi curveto nu sunt instrumente de "grafică pe calculator" (precum de exemplu, funcţiile plot() din R) - ci sunt instrucţiuni proprii pe care PostScript le foloseşte efectiv, în scopul predeclarat de a formula o pagină astfel încât descrierea respectivă să poată fi interpretată la fel pe orice dispozitiv de redare a paginii.
Punctele sunt văzute ca nişte perechi de numere, în sistemul de coordonate curent (şi nu există instrucţiuni pentru a le "trasa" ca atare); punctele vor putea arăta diferit de la un dispozitiv la altul, după cum este "pixelul" sau "punctul tipografic" al acestuia. Dar ansamblul de puncte constituit de un segment sau un arc Bézier va arăta la fel, indiferent de dispozitiv sau scară - mai ales că transformările posibile nu se aplică figurii, ci sistemului de coordonate în care este exprimat conturul; tocmai de aceea, componentele paginii (inclusiv, caracterele) sunt descrise folosind lineto şi curveto.

Literele şi celelalte caractere sunt văzute ca fiind fiecare, un anumit contur închis, format din segmente şi curbe Bézier; astfel, ele îşi păstrează mai bine forma dacă se aplică scalări sau alte transformări - spre deosebire de cazul când ar fi reprezentate static, prin matrici predefinite de puncte.

Prin operatorul charpath putem obţine conturul existent pentru un caracter; de exemplu, (S) false charpath va adăuga conturului curent pe cel asociat pentru litera 'S' în cadrul fontului curent (dacă acest font nu este unul protejat). Iar dacă folosim apoi pathforall (cum am mai arătat), putem afişa secvenţa de instrucţiuni care conturează litera respectivă; în următorul program am preluat din această secvenţă partea care corespunde conturului interior al lui 'S', în fontul Times-Roman:

%!PS-Adobe-2.0 EPSF-2.0
%%BoundingBox: 152 136 270 240

/Times-Roman findfont 18 scalefont setfont

144 144 translate  4 4 scale

% extragem dintr-o sesiune de lucru cu Ghostscript, conturul interior al lui 'S'
3.36217046 -0.464388192 moveto
3.39932156 0.204330802 3.82655883 0.705870092 4.36524916 0.705870092 curveto
4.75533533 0.705870092 5.34975195 0.575841367 6.03704643 0.315783978 curveto
7.39306 -0.204330802 8.86052704 -0.50153923 10.2536917 -0.50153923 curveto
14.3960342 -0.50153923 17.5353 2.30336547 17.5353 6.01847124 curveto
17.5353 8.93482876 15.5662928 11.2010431 10.866684 13.7644663 curveto
7.11442709 15.7891989 5.6098094 17.3495426 5.6098094 19.3185482 curveto
5.6098094 21.26898 7.11442709 22.5878429 9.32491493 22.5878429 curveto
10.92241 22.5878429 12.4270287 21.9191227 13.6715889 20.6374111 curveto
14.7861204 19.4857292 15.2876596 18.5755272 15.8635006 16.4764938 curveto

21 0 moveto  % punctul de start pentru următorul contur
(S) false charpath  % adaugă conturului de mai sus, conturul literei 'S'

.1 setlinewidth  .1 setgray
stroke  % trasează efectiv cele două contururi

1 0 0 setrgbcolor
4.36524916 0.705870092 moveto  % punctează capătul final pentru prima 'curveto'
4.36524916 0.705870092 .2 0 360 arc fill  

% capătul final pentru a doua instrucţiune 'curveto', a treia, etc.

Am marcat cu câte un "cerculeţ" roşu (produs prin arc fill) capătul final al fiecăreia dintre cele 9 bucăţi curveto ale conturului interior al literei (coordonatele cerculeţului sunt date de ultimele două valori din instrucţiunea curveto respectivă); acest contur este de două ori mai mare decât cel corespunzător din conturul literei redat în partea dreaptă a imaginii, fiindcă în sesiunea de lucru cu GS din care l-am preluat am folosit 36 scalefont, în timp ce în programul de mai sus avem doar 18 scalefont:

vb@Home:~/5mai$ gs -q  % sesiune de lucru interactiv în Ghostscript
GS> /Times-Roman findfont 36 scalefont setfont
GS> 0 0 moveto
GS> (S) false charpath
GS> {[3 1 roll (moveto)] == } {[3 1 roll (lineto)] == }
GS<2> {[7 1 roll (curveto)] == } {(closepath) == } 
GS<4> pathforall
[15.9749537 24.0367336 (moveto)]
[15.2133579 24.0367336 (lineto)]
[15.0647535 23.2565613 14.6746674 22.8293247 14.0802498 22.8293247 (curveto)]
...
[6.31567955 0.780172169 4.10519171 2.7306025 2.3219409 7.07727623 (curveto)]
[1.50461781 7.07727623 (lineto)]
[2.56342292 -0.464388192 (lineto)]
[3.36217046 -0.464388192 (lineto)]
[3.39932156 0.204330802 3.82655883 0.705870092 4.36524916 0.705870092 (curveto)]
...
[14.7861204 19.4857292 15.2876596 18.5755272 15.8635006 16.4764938 (curveto)]
[16.755127 16.4764938 (lineto)]
[15.9749537 24.0367336 (lineto)]
(closepath)
[20.015131 0.0 (moveto)]
GS>

Bineînţeles că am folosit {[7 1 roll (curveto)] == }, având în vedere că curveto are 6 parametri (v. §7 pentru roll şi pathforall). Litera este un contur închis (se încheie prin closepath), constituit dintr-un sub-contur "exterior" (în cazul de faţă, cu 10 instrucţiuni curveto) şi unul "interior" (în redarea trunchiată de mai sus l-am indicat prin "bold"), conectate şi completate prin câteva instrucţiuni lineto. Instrucţiunea finală 20.015131 0.0 moveto stabileşte "punctul curent" de la care să înceapă următoarea trasare de contur, dacă există (încât în programul de mai sus am putut estima prin 21 0 moveto, unde să adaug conturul întreg al literei).