Tabelul "Sy" – v. [2] – conține cele 60 de cicluri distincte de lungime 5 ale grafului hexacontaedral G; acestea trec câte cinci, prin câte unul dintre vârfurile 81:92 de grad 5 – încât G se „descompune” în 12 foliaje (numind "foliaj" un set de 5 pentagoane convexe care au un vârf comun și au câte două, o muchie comună).
Anterior doar am plotat, foliajele respective; acum, observând că un „foliaj” reprezintă de fapt un graf cunoscut – graful Jahangir J3,5 (a vedea de exemplu [3]) – vom viza descompunerea în anumite seturi de subgrafuri J3,5.
Gândul inițial era de a justifica faptul că G are numărul cromatic 3 și orice 3-colorare este ”uniformă”; dar găsim și o descompunere în seturi de foliaje, care permite o nouă reprezentare planară ("front-back"), specifică probabil grafurilor poliedrale.

Cele 12 subgrafuri izomorfe unei roți cu 5 spițe

Următoarea funcție reunește cele 5 cicluri din Sy care trec printr-un același vârf; aplicând-o pe fiecare vârf de grad 5, găsim cele 12 foliaje (într-o listă flj, conținând cele câte 16 vârfuri ale fiecărui foliaj):

rejoin <- function(V1) {
    sy5 <- Sy[Sy[, 1] == V1, ]  # cele 5 cicluri prin vârful de grad 5 V1
    c(V1, sy5[, 2:4] %>% as.vector() %>% unlist())
}
flj <- map(81:92, function(v1) rejoin(v1) %>% as.integer())
        81 26 25 23 21 24 46 41 28 22 37  4  3  1  2  5
        82 31 30 29 22 27 56 51 36 21 33  7  6  2  1  8
        83 34 35 33 28 32 80 57 27 23 43 19  8  1  3 20
        84 39 40 37 36 38 79 47 24 29 53 17  5  2  6 18
        85 44 45 43 41 42 76 61 32 25 49 11 20  3  4 10
        86 50 48 47 46 49  9 17  5  4 10 66 40 26 42 69
        87 54 55 53 51 52 71 65 38 30 59 14 18  6  7 13
        88 60 59 56 57 58 70 52 31 35 63 13  7  8 19 12
        89 64 63 80 61 62 72 58 34 45 78 12 19 20 11 15
        90 67 65 79 66 68 14 18 17  9 16 55 39 48 75 73
        91 76 69 75 77 78 44 50 68 74 62 10  9 16 15 11
        92 74 73 71 70 72 77 67 54 60 64 16 14 13 12 15

Subgraful indus în G de fiecare dintre aceste 12 foliaje este un graf izomorf grafului Jahangir – care seamănă unei roți cu 5 spițe din 3 în 3 nituri – fiind compus dintr-un ciclu de lungime 3×5=15 și un al 16-lea vârf (centrul roții) care este adiacent cu 5 noduri ale ciclului, egal distanțate între ele:

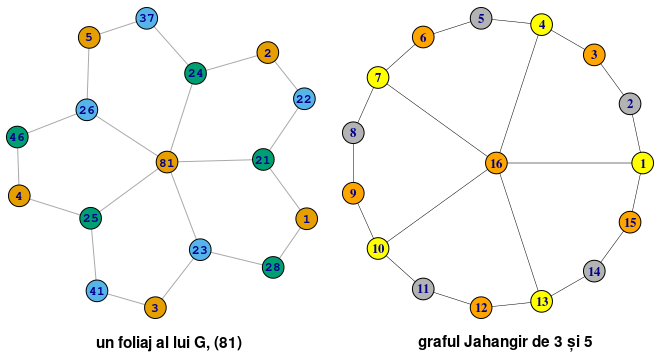
Menționăm că grafurile Js,m au fost introduse de matematicieni pakistanezi, iar numele "Jahangir" ține de cultura indiană (nu se putea numi… "sm-roată", având deja grafuri "Wheel").

În redarea grafică de mai sus, pentru subgraful indus de foliajul (81) am păstrat 3-colorarea lui G, de la care a plecat [2]; pentru graful J3,5 am constituit ad-hoc o 3-colorare: ne trebuie două culori pentru vârful central și respectiv, cei 5 adiacenți ai acestuia – iar pentru celelalte 10 vârfuri am alternat în sens orar, culoarea vârfului central și o a treia culoare.
E clar că și într-un caz și în celălalt, avem o 3-colorare uniformă: 6 noduri pe culoarea centrală și câte 5 pe celelalte două culori; este de bănuit că orice 3-colorare a lui G, trebuie să fie și ea, uniformă (32, 30, 30 – v. [2])…

Subgrafurile F6 – compuse din câte 6 foliaje, cu unul central

Este ușor de constatat că fiecare dintre cele 12 foliaje are în comun cu alte câte 5 foliaje, câte exact patru vârfuri îmbinate pe o cale de lungime 3:

for(i in 1:12) {
    print(80+i)
    for(j in (1:12)[-i]) {
        com <- intersect(flj[[i]], flj[[j]])
        if(length(com) > 0) {
            cat(80+j, ": ")
            print(com)
        }
    }
    cat("\n")
} # De exemplu, pentru foliajul (81), centrat în 81:
        [1] 81
        82: [1] 21 22  1  2  # 3 muchii comune cu foliajul (82)
        83: [1] 23 28  3  1  # calea 23--28--3--1 în comun cu (83)
        84: [1] 24 37  2  5
        85: [1] 25 41  4  3
        86: [1] 26 46  4  5

Cu alte cuvinte, dacă așezăm în centrul paginii foliajul (81) atunci îi vom putea alipi, pe câte 3 muchii consecutive ale sale, foliajele (82)..(86); la fel, foliajului (82) îi vom putea alipi pe câte 3 muchii consecutive ale sale, foliajele (81), (83), (84), (87) și (88) – ș.a.m.d., pentru fiecare dintre cele 12 foliaje.

Deci un foliaj oarecare induce împreună cu cele 5 foliaje cu care are în comun câte o cale de lungime 3, un subgraf al lui G – să-l numim generic F6 – care conține 61 de vârfuri și 90 de muchii (dintre cele 92 de vârfuri și 150 de muchii ale lui G).
Într-adevăr, cele 6 „foliaje” care compun F6 ar avea în total 6×20=120 de muchii, dar trebuie să scădem o dată cele 3×5=15 muchii comune cu foliajul central și a doua oară cele 5×3=15 muchii comune la câte două dintre cele 5 foliaje din jurul celui central – deci F6 are 120-30=90 muchii distincte.
Analog pentru vârfuri: J3,5 are 16 vârfuri, deci în total ar fi 16×6=96 de vârfuri; dar foliajul central are în comun cu celelalte 5 câte 4 vârfuri și pentru a nu le socoti de două ori, avem de scăzut 4×5=20 de vârfuri; dintre cele 76 de noduri rămase trebuie să excludem (pentru a nu le număra de două ori) cele câte 3 noduri (al patrulea este pe foliajul central și deja l-am exclus) comune la câte două dintre cele 5 foliaje din jurul celui central, deci încă 3×5=15 noduri – încât în final avem în F6 exact 96-35=61 de vârfuri.

Avem 12 subgrafuri F6, după cum alegem ca foliaj central unul dintre cele 12 foliaje din lista flj. Ca exemplu, producem și plotăm mai jos, pe cel centrat în (81).

Invocăm igraph::induced_subgraph() pentru reuniunea vârfurilor din foliajele (81)..(86) și simplificăm numele vârfurilor subgrafului rezultat (eliminând prefixul "V"):

F6 <- induced_subgraph(G, flj[1:6] %>% unlist() %>% unique())
V(F6)$name <- gsub("V", "", V(F6)$name)  # simplificăm numele ("V81" devine "81", etc.)

Vrem să marcăm muchiile foliajului central; pentru aceasta, trebuie întâi… să le găsim (dar nu manual). Putem proceda astfel: considerăm subgraful J3,5 indus de foliajul (81), îi găsim – prin funcția find_cycles() din [2] – ciclul de lungime 15 care formează „roata” și apoi, prin rbind(), constituim secvența muchiilor acestui ciclu (înlănțuind capetele pe două rânduri):

g1 <- induced_subgraph(G, flj[[1]])  
cy1 <- find_cycles(g1, 15)[1] %>% unlist() %>% names()
cy1 <- gsub("V", "", cy1)
edg1 <- rbind(cy1, c(cy1[2:length(cy1)], cy1[1]))
    [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13] [,14] [,15]
cy1 1    28   23   3    41   25   4    46   26   5     37    24    2     22    21
    28   23   3    41   25   4    46   26   5    37    24    2     22    21    1

edg1 conține cele 15 muchii ale ciclului, 1--28, 28--23, ..., 22--21, 21--1 (și am evitat „lucrul manual”; putem proceda la fel și dacă am baza F6 nu pe (81), ci de exemplu pe (82), sau pe altul dintre cele 12 foliaje); să-i adăugăm și cele 5 „spițe” ale foliajului (81) și apoi, prin igraph::get.edge.ids() putem identifica muchiile respective în cadrul grafului F6:

edg1 <- c(as.vector(edg1), strsplit(paste(81, (21:26)[-2]), " ") %>% unlist())
Edg <- get.edge.ids(F6, as.character(edg1))  # indecșii din F6 pentru muchiile lui (81)

Acum putem plota subgraful F6, cam așa (preferăm să nu marcăm și 3-colorarea):

coords <- layout_nicely(F6)  # saveRDS(coords, "coords.RDS")
old_par <- par(mar=c(0,0,0,0), cex=0.8, bty="n", xaxt="n", yaxt="n")
plot(F6, layout = coords,
     vertex.size = 6, vertex.frame.width = 0.25, edge.width = 0.7,
     vertex.label.family = "mono", vertex.label.font = 2, 
     vertex.color = ifelse(V(F6)$name %in% as.character(81:86), "gray90", NA),
     edge.color = ifelse(E(F6) %in% Edg, "tomato", "slategray"),
)
par(old_par)

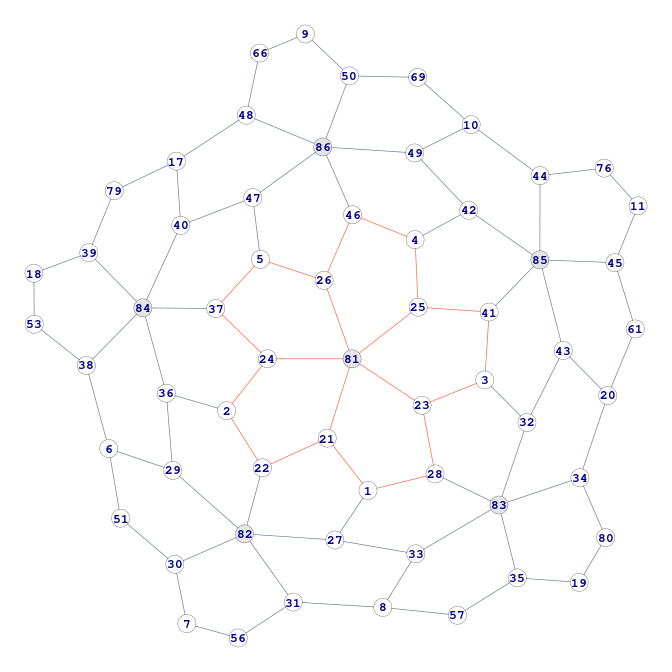
De remarcat că layout_nicely() a așezat elegant foliajele (82)..(86) – într-un format pentagonal – în jurul foliajului central (81); este drept că repetând execuția, pot rezulta și reprezentări neplanare (fiindcă igraph::layout_() implică și variabile aleatorii).

Este cam de la sine înțeles, că toate grafurile F6 deduse ca mai sus, sunt izomorfe între ele – conținând câte 6 subgrafuri J3,5 care sunt la fel așezate, în jurul câte unuia dintre ele (de altfel, putem și verifica, folosind igraph::subgraph_isomorphisms()).

Colorarea grafului F6

Privind F6 ca graf de sine stătător (și nu neapărat ca subgraf al lui G), putem constata folosind greedy_color_by_centrality() din [2], că F6 are o 3-colorare uniformă:

> F6 <- greedy_color_by_centrality(F6)
> table(V(F6)$color)  # 21 20 20

Folosind în plot() (mai sus) vertex.color=V(F6)$color, putem și vizualiza colorarea respectivă; dar problema ar fi „de ce” F6 are o 3-colorare care este neapărat, uniformă…

E clar deja, că orice foliaj are o 3-colorare și aceasta este neapărat, uniformă; să fixăm colorarea foliajului central (81) al lui F6 (graful tocmai redat mai sus) – de exemplu aceea redată la început pentru J3,5: vârful central 81 are culoarea "1", adiacenții acestuia au culoarea "2", iar celelalte 10 vârfuri alternează în sens orar culorile "1" și "3".

Din colorarea fixată foliajului central se pot deduce colorările aferente celorlalte 5 foliaje din F6 – poate nu în mod unic, dar ne putem da seama că se păstrează uniformitatea repartizării pe vârfuri a culorilor; schițăm raționamentul respectiv, de exemplu pentru cazul foliajului (85), care are în comun cu (81) calea 4--25--41--3, marcată pe figură:

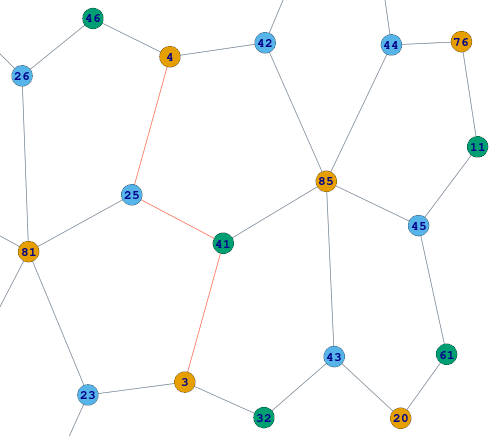
Din colorarea pe care am fixat-o pentru (81), rezultă că nodurile 4, 25, 41, 3 au respectiv culorile "1", "2", "3" și "1"; vârful 85 poate fi colorat fie cu "1", fie cu "2" (dar nu cu "3", fiindcă adiacentul său 41 are culoarea "3"), iar vârfurile 42 și 32 pot fi colorate fie cu "2", fie cu "3"; pentru oricare dintre aceste posibilități, găsim câte o colorare a lui (85) de același tip ca aceea a lui (81) – încât în final, rezultă 3-colorări uniforme ale lui F6.

O reprezentare planară "front-back", a grafului poliedral

Să notăm cu S1 subgraful F6 considerat mai sus, indus de reuniunea foliajelor (81)..(86).
Fie S2 subgraful indus de celelalte 6 foliaje, (87)..(92); în centru avem (92), fiindcă acesta are câte trei căi de lungime 3 cumune cu celelalte 5 foliaje din S2.
Grafurile F6 sunt izomorfe între ele, deci S1 și S2 sunt grafuri izomorfe.

Împreună, S1 și S2 formează o partiție a grafului G; deci ele au în comun 61+61 - 92=30 de vârfuri – și observând imaginea redată mai sus, deducem că aceste 30 de vârfuri constituie ciclul „exterior” al fiecăruia, 9 -- 50 -- 69 -- 10 -- 44 -- ... -- 17 -- 48 -- 66 -- 9. Dar vom vedea mai jos că acest ciclu comun – la care ne vom referi prin $\mathcal{Q}$ – nu este și „la fel”, în S1 și S2…

Această partiționare a lui G în subgrafurile S1 și S2 ar corespunde cam la ceea ce am vedea din poliedrul reprezentat prin G, când îl privim dintr-un anumit punct exterior lui și respectiv, din punctul diametral opus față de centrul poliedrului; „din față”, vedem scheletul poliedral corespunzător lui S1, cam așa (am marcat centrele celor 6 foliaje):

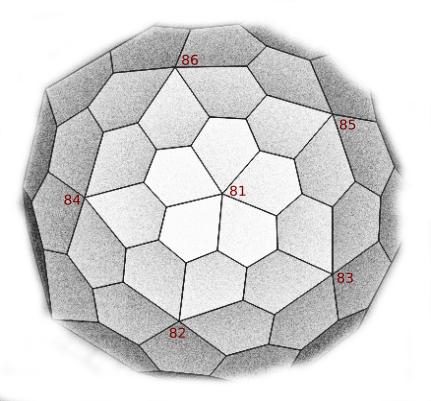
poliedrul hexacontaedral

iar „din spate” vom vedea scheletul corespunzător lui S2. Desigur, între cele două vederi avem o anumită inversare: „stânga” într-un caz, devine „dreapta” în celălalt!.

30-ciclul comun $\mathcal{Q}$ se vede într-un fel „din față” și în alt fel, „din spate” – fiindcă montarea lui diferă între S1 și S2, cum ne arată gradele unor vârfuri consecutive din $\mathcal{Q}$:

> Path <- c("V9", "V50", "V69", "V10")  # o cale de pe 30-ciclul comun
> lapply(list(S1, S2), degree, Path) %>% unlist() %>% 
      matrix(., ncol=4, byrow=TRUE, dimnames=list(c("S1","S2"), Path))
           V9 V50 V69 V10
        S1  2   3   2   3
        S2  3   2   3   2

Vârfurile din $\mathcal{Q}$ care au în S1 gradul 2 (respectiv 3), au în S2 gradul 3 (respectiv 2); prin urmare, orice izomorfism între S1 și S2 va transforma $\mathcal{Q}$ tot în $\mathcal{Q}$, dar fără puncte fixe (v∈$\mathcal{Q}$ este dus într-un w∈$\mathcal{Q}$, dar astfel încât w≠v; avem v „în stânga” lui S1 și w „în stânga” lui S2).

Constituim cele două subgrafuri S1 și S2 și considerăm unul dintre izomorfismele (în număr de 5) existente între acestea:

S1 <- induced_subgraph(G, flj[1:6] %>% unlist() %>% unique())  # de centru (81)
S2 <- induced_subgraph(G, flj[7:12] %>% unlist() %>% unique())  # de centru (92)
izm <- subgraph_isomorphisms(S1, S2)[[1]] %>% as.integer()

Inspectând izm, V(S1) și V(S2) ne putem lămuri eventual, ce asociere (care păstrează adiacența) s-a făcut între S1 și S2.

Putem obține acum, o reprezentare (planară) „față-spate” a grafului G, plotând S1 și etichetând nodurile conform izomorfismului izm:

l1 <- V(S2)$name[izm]  # vârfurile lui S2 în ordinea indusă de izomorfism
l2 <- V(S1)$name
l1 <- gsub("V", "", l1)  # omite "V" din numele vârfurilor
l2 <- gsub("V", "", l2)
fs <- rbind(l2, l1)  # vârfurile S1 pe un rând, cele asociate în S2 dedesubt
Labels <- vector("character", length(fs))
for(i in 1:ncol(fs))
    Labels[i] <- str_flatten(fs[, i], "-")  # etichete ca "9-17", din cele 2 rânduri
fol <- Labels[56:61]  # centrele foliajelor (de marcat, prin culoare)
old_par <- par(mar=c(0,0,0,0), cex=0.8, bty="n", xaxt="n", yaxt="n")
plot(S1,  # implicit, layout_nicely()
     vertex.size = 4, vertex.frame.width = 0.25, 
     vertex.label.family = "mono", vertex.label.font = 2,
     vertex.label = Labels, 
     vertex.color = ifelse(Labels %in% fol, "gray80", NA), 
     edge.color = "slategray", edge.width = 0.7,
)
par(old_par)

Reprezentarea obținută (redată aici cu 75%) satisface scopul principal, de a evidenția adiacența; de exemplu în jurul nodului etichetat "18-10" avem și adiacenții vârfului 18 (vârfurile 39 și 53) și pe cei ai vârfului 10 (anume 69 și 44).

Putem trata cam la fel ca în cazul de mai sus al hexacontaedrului pentagonal și poliedre din clasele obișnuite (dacă nu sunt prea „neregulate”): vom avea un izomorfism între ceea ce vedem „din față” și respectiv, „din spate” și atunci, putem asocia poliedrului (după ce îi etichetăm vârfurile) o reprezentare planară "front-back" (am avea o cea mai simplă exemplificare, alegând cubul, sau un dodecaedru).