Un "intermezzo" conjunctural din [1] m-a găsit să întreb: Care este la noi, cel mai important și respectiv, cel mai puțin important obiect? — dar m-am găsit să răspund doar sarcastic: cel mai important este Religie – are o oră pe săptămână, dar la toate clasele din țară; cel mai puțin importante sunt „muzica” și „desenul” – au câte o jumătate de oră pe săptămână și numai la unele clase.

Reluăm întrebarea, încercând să-i dăm un sens: să clasificăm cumva obiectele, după interferențele induse de planul anual de încadrare al școlii. Încadrarea alocă profesori, clase și număr de ore, pentru fiecare disciplină școlară; interferența a două obiecte ar fi dată de numărul de intrări la aceleași clase, ale profesorilor încadrați pe cele două obiecte.

De exemplu, să observăm că toate clasele fac „Educație fizică” (Ef) – dar măcar la unele clase, pe câte două ore; deci Ef devine mai important decât „Religie” – cel puțin fiindcă este de așteptat ca numărul de profesori pe Ef să fie ceva mai mare decât pe Re.
Dar „numărul de profesori” este oarecum înșelător: de exemplu, sunt 4 profesori de Ef – dar unul are doar câteva ore (un sfert de normă, să zicem); în loc să vizăm direct numărul de profesori pe fiecare disciplină, vom cumula intrările pe clasele comune câtor doi profesori.

Pe de altă parte, „importanța” unui obiect (sau… profesor) depinde și de importanța obiectelor cu care el interferează pe diverse clase. De exemplu, M („Matematică”) se face la toate clasele, dar nu pe câte un același număr de ore; nu-i totuna să faci un obiect sau altul la o clasă care are alocate 5 ore de M, respectiv la una cu doar două ore de M…

Obs. În [1] am arătat că alocând pe orele zilei lecțiile prof|cls ale zilei curente, într-o ordine derivată din interferențele profesorilor la clase – putem obține mult mai sigur și mai rapid un orar al zilei, decât dacă am respecta ordinea obișnuită (dată de numărul de ore, crescător sau descrescător).

Precizăm că aici nu aspirăm la vreun rezultat remarcabil, ci doar ilustrăm o manieră tipică pentru depistarea unor comunități într-o rețea socială; în principiu, membrii unei aceleiași comunități au mai multe conexiuni între ei, decât spre exteriorul acesteia.

Considerăm una dintre școlile pe care am experimentat programele dezvoltate în [1]:

> str(LSS %>% slice_sample(., n=nrow(.)), vec.len=12, give.head=FALSE)
'data.frame':	1260 obs. of  2 variables:  (109 profesori, 42 clase)
 $ prof:"Bi1" "M04" "Ch2" "Gg2" "M02" "R05" "En3" "Ge1Ge2" "Fi3" "N03X01" "N02" "Ec1" ...
 $ cls :"9C" "11H" "9A" "8B" "6A" "11G" "11G" "9A" "12B" "9H" "11H" "11B" ...

Încadrarea prevede 1260 de lecții săptămânale prof|cls (și am redat un eșantion aleatoriu de 12 lecții); sunt 83 de profesori (codificați după disciplinele principale, abreviate prin una sau două litere), plus 26 de cuplaje (de exemplu, "Ge1Ge2" acoperă lecțiile de „Germană” desfășurate împreună – pe grupe ale claselor respective – de către "Ge1" și "Ge2") și sunt 42 de clase.

Sunt 29 de obiecte (discipline școlare), dar aici le vom păstra numai pe cele principale, derivate direct din codurile profesorilor:

Frame <- LSS %>% mutate(obj = str_extract(prof, "^\\D+"), .before=1)

De exemplu, orele de „Cultură germană” (câte o oră la vreo două clase) le-am inclus la „Germană” (Ge); cele vreo două ore de „Cultură civică” ale lui Em1 și cele câteva ore ale lui Ev1, le-am inclus la „Educație muzicală/vizuală” (orele de bază pentru Em1Ev1); la fel, cele vreo 6 lecții înregistrate pe „Dirigenție” le-am inclus respectiv, obiectelor asociate profesorilor cărora li s-a explicitat în încadrarea dată câte o dirigenție.

Graful interferențelor între profesori

Constituim întâi un graf (presupunem că am încărcat pachetele tidyverse și igraph) având drept noduri cei 109 profesori și în care muchia Pi--Pj indică numărul de intrări comune la clase – însumând cele mai mici dintre numerele de ore la clasele comune, ale profesorilor Pi și Pj:

lPC <- Frame %>% split(.$prof) %>% 
       map(., function(X) unique(X$cls))  # Prof ==> vectorul claselor proprii
nP <- length(lPC)
Prof <- names(lPC)
Wgt <- matrix(rep(0, nP*nP), nrow = nP, ncol = nP, byrow = TRUE, 
              dimnames = list(Prof, Prof))  # matricea de adiacenţă (ponderi)
tPC <- table(Frame[c('prof','cls')])  # câte ore are fiecare profesor la fiecare clasă
for(p1 in Prof)
    for(p2 in setdiff(Prof, p1)) {  # conexiunile cu ceilalți
        mins <- 0
        for(k in intersect(lPC[[p1]], lPC[[p2]]))  # pe clasele comune
            mins <- mins + min(tPC[p1, k], tPC[p2, k])
        Wgt[p1, p2] <- mins  # ponderea muchiei
    }
Ginf <- graph_from_adjacency_matrix(Wgt, mode="undirected", weighted = TRUE)

De exemplu, Bi1 și Fi6 interferează pe câte 2 ore la clasele 9A și 9B și pe o oră la 11E – deci muchia "Bi1|Fi6" din graful Ginf are ponderea 5:

> p1 <- "Bi1"; p2 <- "Fi6"
> tPC[c(p1, p2), intersect(lPC[[p1]], lPC[[p2]])]
             cls
        prof  9A 11E 9B
          Bi1  2   1  2
          Fi6  3   3  3
> E(Ginf)["Bi1|Fi6"]$weight  # [1] 5 (intrări "comune" pe aceleași clase)

Fiecare profesor interferează (în sensul învederat în graful Ginf) cu alți profesori – care la rândul lor, interferează (mai mult sau mai puțin) cu alții. Deci „importanța” (sau centralitatea) profesorului ar fi dată cumva recursiv, cumulând centralitățile adiacenților acestuia în rețeaua Ginf; A fiind matricea de adiacență, iar x vectorul căutat al centralităților vârfurilor – ar trebui să avem Ax = λx, unde λ ar fi o constantă pozitivă cât se poate de mare.
Teorema Perron–Frobenius ne asigură că există o valoare maximă λ ("eigenvalue" sau „raza spectrală” a matricei A) pentru care sistemul de ecuații menționat are soluție unică.

Funcția igraph::eigen_centrality() produce pentru graful indicat (asumând în A ponderile muchiilor), o listă care conține valoarea λ și vectorul x:

lEIG <- eigen_centrality(Ginf, scale=FALSE)
rad <- lEIG$value  # λ
egv <- lEIG$vector  # centralitățile nodurilor (vectorul x)
    # Să verificăm că A*x = λ*x:
M <- Wgt %*% egv  # A*x
all.equal(M[, 1], rad*egv, tolerance = 1e-5)  # TRUE

Subliniem că M este o matrice, având în prima coloană nodurile lui Ginf (numele profesorilor), iar în a doua (selectată mai sus prin M[, 1]) produsele scalare dintre câte o linie a matricei de ponderi Wgt și vectorul x (= egv); "%*%" este operatorul de înmulțire matriceală.
În M[1, ], numele profesorilor sunt în aceeași ordine ca aceea din vectorul cu nume x – încât am putut testa direct, egalitatea Ax=λx (cu eroare mai mică de 10^-5).

De exemplu, în cazul nostru, avem:

> egv[c("M01", "Re1")]  # centralitățile a două noduri
           M01        Re1 
    0.08466074 0.22483063 
> Ginf["M01", ] %>% sum()  # 131 (numărul de muchii incidente nodului)
> Ginf["Re1", ] %>% sum()  # 324
> degree(Ginf)["M01"]  # 42 (numărul de adiacenți)
> degree(Ginf)["Re1"]  # 88

adică Re1 este „mai important” (0.22 > 0.08) decât M01. Într-adevăr, M01 are câte 4 ore la 5 clase – deci are câte cel mult 3 (excepțional, 4) interferențe (pe fiecare clasă) cu ceilalți 42 de profesori ai acestor cinci clase (rezultând 131 de interferențe); în schimb Re1 are câte o oră la 24 de clase, astfel că interferează cu 88 de profesori, cumulând câte o muchie comună cu aceștia la fiecare dintre aceste 24 de clase (rezultând în total, 324 de interferențe).

Dar aceasta nu înseamnă că Re este mai important decât M – fiindcă avem 10 profesori de „Matematică” și numai doi de „Religie”; multiplicând corespunzător coeficienții găsiți mai sus, găsim că M ar fi „mai important” decât Re (10×0.8 > 2×0.22) – dar acest calcul este unul expeditiv; mai corect ar fi să însumăm centralitățile celor 10 și respectiv, celor doi și apoi să comparăm cele două sume.

Graful interferențelor între obiecte

Să constituim un graf al obiectelor, în care o muchie să aibă ca pondere cea mai mică dintre sumele centralităților din vectorul egv, pentru profesorii încadrați pe câte unul dintre cele două obiecte incidente muchiei respective:

lo <- Frame %>% split(.$obj)  # lista încadrărilor pe obiecte
Obj <- names(lo)
len <- length(Obj)
wgt <- matrix(rep(0, len*len), nrow=len, ncol=len, byrow=TRUE, 
              dimnames = list(Obj, Obj))  # matricea de adiacenţă (ponderi)
for(o1 in Obj) {
    P1 <- unique(lo[[o1]]$prof)
    c1 <- sum(egv[P1])  # pentru profesorii de pe primul obiect
    for(o2 in setdiff(Obj, o1)) {
        P2 <- unique(lo[[o2]]$prof)
        c2 <- sum(egv[P2])  # pentru cei de pe celălalt obiect
        wgt[o1, o2] <- min(c1, c2)  # "interferența" celor două obiecte 
    }
}
Gob <- graph_from_adjacency_matrix(wgt, mode="undirected", weighted=TRUE)

În graful Gob centralitățile nodurilor (obiectelor), în ordine crescătoare, sunt:

> eigen_centrality(Gob, scale=FALSE)$vector %>% sort() %>% print()
        Es         Et         TI         Ps         Ge         Ec         Fs 
0.03425777 0.03891029 0.03903099 0.06601035 0.07769435 0.11466757 0.11641341 
        mv         Re         Gg         Is         Ef         Ch         Bi 
0.19382823 0.23621676 0.24057797 0.24745861 0.26851929 0.27046675 0.27630987 
        Fr         En         Fi          R          N          M 
0.28014408 0.29086539 0.29644758 0.29993767 0.30305448 0.30305448 

S-ar confirma astfel, aserțiunile anterioare: Ef este „mai important” ca Re, Re este mai important ca mv, iar M este mai important ca toate celelalte…

Dar dacă e să vedem vreo comunitate în rețeaua Gob, atunci trebuie să „vedem” cumva și muchiile (pe lângă centralitățile nodurilor, găsite mai sus) – fiindcă nodurile dintr-o aceeași comunitate sunt mai bine conectate (prin muchii) decât nodurile din comunități diferite (și… rămâne să lămurim cumva, ce poate însemna „mai bine conectate”).
În cazul de față (rețeaua fiind una relativ mică) ar fi suficient probabil, să vizualizăm graful respectiv și să apreciem „din ochi” densitatea muchiilor:

library(ggraph)  # v. https://cran.r-project.org/web/packages/ggraph
Dobj <- readRDS("STRUC/Obiecte.RDS")  # dicționar Cod_obj ==> Nume_obj
eig_cen <- eigen_centrality(Gob)$vector 
V(Gob)$eig_cen <- round(eig_cen, 3)
set_graph_style(plot_margin = margin(1,1,1,1))
gg <- ggraph(Gob, layout = "fr") +
      scale_edge_width(range = c(0.3, 2)) +
      geom_edge_link(aes(width = weight), color = "grey", alpha = 0.8) +
      geom_node_point(aes(alpha = eig_cen, size = 16)) +
      geom_node_text(aes(label = Dobj[name]), repel = TRUE) + 
      theme_void()
plot(gg)

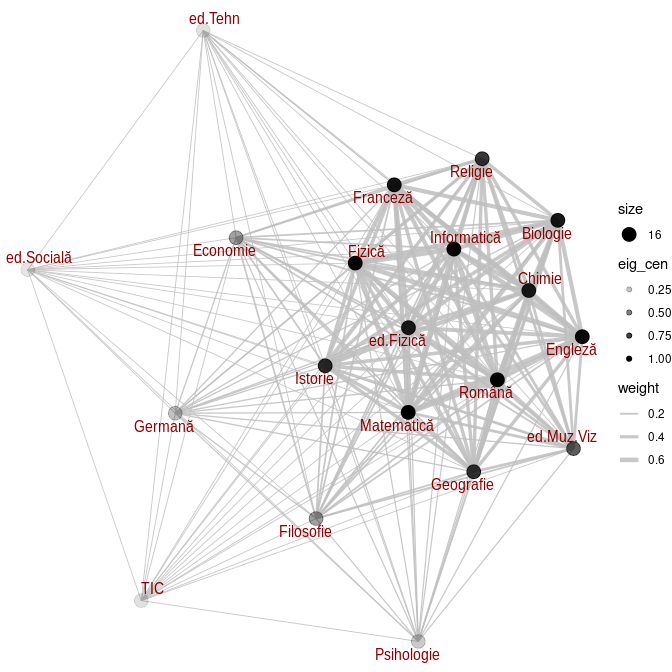
Prin Dobj (și geom_node_text()) am putut eticheta nodurile cu numele obișnuite ale obiectelor (de exemplu, avem Dobj["Bi"]="Biologie").
În eig_cen am recalculat centralitățile vârfurilor, dar acum cu valoarea implicită a parametrului 'scale' – scalând valorile respective față de cea maximă; le-am rotunjit apoi la 3 zecimale și le-am înscris ca proprietate a nodurilor grafului Gob – exploatând-o apoi prin geom_node_point(), cum se vede în legenda 'eig_cen' a graficului redat mai sus.
Am procedat analog pentru muchii (v. legenda 'weight'), folosind scale_edge_width() și angajând în geom_edge_link() proprietatea E(Gob)$weight asociată muchiilor (reflectând deci nu muchiile ca atare, ci ponderile acestora).

Pe grafic se vede că zona care conține nodurile marcate cu eig_cen cuprins între 0.75 și 1 are o densitate mult mai mare de muchii, decât complementara ei – ceea ce este un semn că în această zonă, ar trebui să depistăm o comunitate; rămâne totuși să verificăm dacă legăturile spre exterior ale celor 12 noduri (dacă nu ne înșală ochii) din această zonă, sunt într-adevăr mai puține decât cele interne…
Cu alte cuvinte, rămâne să vedem cât de bună ar fi drept comunitate, zona indicată.

Modularitatea diviziunii

Subliniem că în noua teorie, interdisciplinară, a rețelelor (v. Network science) se vizează partiționarea în comunități (și nu atât, depistarea uneia singure); când ar fi numai două părți, putem zice ca mai sus „legăturile spre exterior” – altfel, am avea de comparat legăturile interioare câte unui grup cu fiecare dintre cele care îl leagă de câte unul dintre celelalte grupuri.

Să zicem deocamdată că în Gob am avea numai două comunități – cum am intuit de pe graficul redat mai sus; atunci (în principiu) putem verifica ușor în ce măsură partiția rezultată convine ideii de comunități: considerăm subgraful G1 indus de cele 12 noduri pe care le-am remarcat mai sus, apoi subgraful G2 indus de celelalte 8 noduri – și ne rămâne să calculăm anumite diferențe între numerele de muchii din Gob, G1 și respectiv G2 (cu observația că nu de „muchii” trebuie să ținem seama, ci de ponderile asociate):

cm1 <- V(Gob)[V(Gob)$eig_cen >= 0.75]  #  [1] Bi Ch Ef En Fi Fr Gg Is M  N  R  Re
G1 <- induced_subgraph(Gob, cm1)
cm2 <- V(Gob)[V(Gob)$eig_cen < 0.75]   #  [1] Ec Es Et Fs Ge mv Ps TI
G2 <- induced_subgraph(Gob, cm2)
s <- sum(E(Gob)$weight)  # ponderea totală a muchiilor (din Gob)
s1 <- sum(E(G1)$weight)  # pentru muchiile din G1
s2 <- sum(E(G2)$weight)  # pentru muchiile din G2
print(c(s, s1, s2))  # [1] 48.884003  33.248668  2.363333
> s - (s1 + s2)  # [1] 13.272 (ponderea conexiunilor dintre G1 și G2)

Constatăm că pentru cm1 ponderea conexiunilor interne (33.25) depășește pe aceea a conexiunilor dintre cm1 și cm2 (13.27); însă conexiunile interne lui cm2 au o pondere (2.36) mult prea mică față de 13.27 – deci cm1 și cm2 nu constituie o divizare în comunități pentru Gob (în orice caz – n-ar fi una tocmai „bună”).
Desigur, am putea muta un vârf (sau două) din cm1 în cm2 – mărind astfel s2 (dar și diferența de mai sus), sau am putea interschimba niște noduri între cm1 și cm2… Până la urmă, probabil că și mai bine ar fi să vizăm nu două, ci (dacă există) trei sau mai multe comunități.

Funcția modularity() estimează calitatea unei partiții în comunități, comparând distribuția muchiilor în grupurile respective cu aceea rezultată într-o rețea artificială care păstrează ponderile vârfurilor, dar în care muchiile sunt generate aleatoriu (v. Modularity).
cm1 introdus mai sus conține (cum ne arată str(cm1)) nu numai numele nodurilor (redate mai sus), dar și atribute prin care se referă graful Gob și se indică indecșii în Gob ai nodurilor respective; as_membership() folosește aceste atribute și ne permite să obținem un vector care indică apartenența vârfurilor 1..20 din Gob la cele două comunități considerate „din ochi” mai sus; putem apoi invoca modularity():

C1 <- as_membership(cm1) %>% as.vector()  # indecșii vâfurilor din Gob aflate în cm1
mbs <- sapply(1:20, function(v) 
           ifelse(v %in% C1, 1, 2)
)  # [1] 1 1 2 1 1 2 2 1 1 2 2 1 1 1 2 1 2 1 2 2  (apartenența vârfurilor la comunități)
print(modularity(Gob, mbs, weights = E(Gob)$weight))  # [1] 0.02388545

Se consideră că partiția respectivă este bună, dacă modularitatea este în jur de 0.3; în cazul nostru avem doar 0.024, deci partiția respectivă este destul de „slabă” (confirmând concluzia rezultată direct, prin calculul sumelor de ponderi redat mai sus).

Căutarea directă a unei partiții acceptabile

Dacă știm numărul NC de comunități (și dacă rețeaua este relativ mică), atunci am putea găsi o partiție acceptabilă procedând astfel: generăm aleatoriu un număr suficient de mare (să zicem, 10⁵) de partiții cu NC părți și reținem acea partiție care are cea mai mare modularitate.

Să căutăm o partiție cu NC=2 care să fie cât mai bună; din cele văzute mai sus este clar că putem ignora acele partiții în care una dintre părți are mai puțin de 5 elemente:

rnd_takeship <- function() {
    repeat {
        mbsh <- sapply(1:20, function(i) sample(1:2, 1))
        if(length(mbsh[mbsh == 1] > 4)) break  # ignoră părți prea mici
    }
    mbsh
}
Part <- map_df(1:100000, function(i) {
            mbs <- rnd_takeship()
            data.frame(ship = paste0(mbs, collapse=""), 
                       mody = round(modularity(Gob, mbs, weights=E(Gob)$weight), 3))
})

Repetând această secvență de câteva ori am obținut – cam în câte 90 secunde – partiții cu modularitatea cuprinsă în intervalul [-0.04,0.029]:

> Part %>% arrange(desc(mody)) %>% head(4)
                     ship  resl
     22122112211222121221  0.029  # v. cm1 și cm2
     22122112211222221221  0.029
     22122112211222121211  0.024
     11211221122211212122  0.021

Deci nu este de crezut că ar exista o partiție în două comunități a rețelei Gob care să aibă modularitatea mai mare ca 0.03…
Maximul rezultat 0.029 vizează într-un caz chiar cm1 și cm2 specificate deja mai sus:

> cms <- strsplit("22122112211222121221", "")[[1]] %>% as.integer() %>%
         setNames(V(Gob)$name)
> cms
    Bi Ch Ec Ef En Es Et Fi Fr Fs Ge Gg Is  M mv  N Ps  R Re TI 
     2  2  1  2  2  1  1  2  2  1  1  2  2  2  1  2  1  2  2  1 

Pentru partiții cu NC=3 (după adaptarea corespunzătoare în funcția rnd_takeship()), modularitatea maximă rezultată prin secvența de mai sus este de ordinul miimilor (și este pozitivă în foarte puține cazuri); pentru NC=4, toate partițiile rezultate au modularitate negativă (în intervalul [-0.058, -0.002], într-una dintre execuții).

Subliniem că procedura (simplă) descrisă mai sus poate fi practicată numai dacă avem de-a face cu o rețea de mici dimensiuni (cum este cazul grafului Gob)…

Depistarea în mod standard, a comunităților

Să aplicăm pentru Gob unul dintre algoritmii de divizare în comunități a unei rețele de mari dimensiuni (cel dat prin anii 2000 de către M. E. J. Newman):

cm <- cluster_leading_eigen(Gob)
plot(cm, Gob, edge.width = 0.7, 
              edge.lty = c(1, 2)[crossing(cm, Gob) + 1])
print(cm)
    IGRAPH clustering leading eigenvector, groups: 2, mod: 0.029
    + groups:
      $`1`  [1] "Bi" "Ch" "Ef" "En" "Fi" "Fr" "Gg" "Is" "M"  "N"  "R"  "Re"
      $`2`  [1] "Ec" "Es" "Et" "Fs" "Ge" "mv" "Ps" "TI"

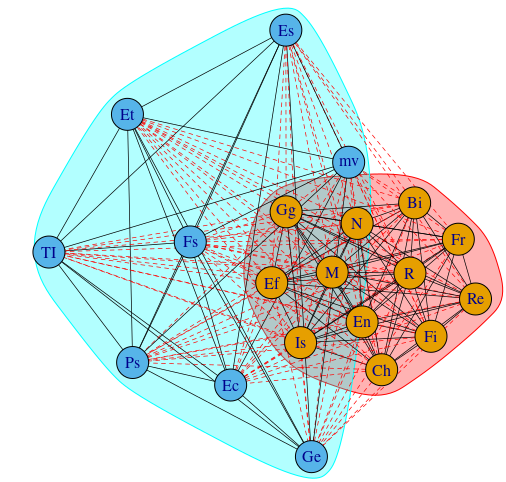
Precizăm că metoda crossing() asociată diviziunii, returnează TRUE sau FALSE (deci 2 sau 1, după ce adunăm cu 1) după cum muchia respectivă unește vârfuri dintr-un același grup, sau din grupuri diferite – astfel că (prin edge.lty) muchiile (colorate implicit, cu negru respectiv roșu) au fost trasate cu tipul de linie "solid", respectiv "dash".

Să observăm că au rezultat cele două comunități evidențiate anterior (cm1 și cm2), cu aceeași modularitate (0.029) ca aceea determinată prin încercările directe anterioare.

Dacă repetăm execuția de mai multe ori, divizarea și modularitatea nu se schimbă – spre deosebire de varianta în care am folosit cluster_spinglass(), când în unele repetări (variind eventual parametrul 'gamma', de exemplu cu gamma=0.94, sau cu gamma=1.06) nodul "mv" este trecut în cealaltă comunitate, sau chiar sunt produse mai mult de două comunități:

IGRAPH clustering spinglass, groups: 3, mod: -4.6
+ groups:
  $`1`   [1] "Ec" "Es" "Et" "Fs" "Ge" "Ps" "TI"
  $`2`   [1] "Gg" "Is" "mv" "Re"
  $`3`   [1] "Bi" "Ch" "Ef" "En" "Fi" "Fr" "M"  "N"  "R" 

O asemenea clasificare în 3 părți, cu modularitate foarte joasă, ar fi de luat în seamă numai în vreun caz în care ar fi de preferat ca pentru unele grupuri să avem mai multe legături între ele, decât în interiorul fiecăruia (iar cluster_spinglass() permite și asemenea favorizări, prin parametrul 'gamma').