Lecţii şi câştiguri

Început de an şcolar, cândva undeva; oră de matematică, cu elevi tocmai sosiţi în clasa a IX-a (orientaţi prin "Examenul Naţional de Evaluare"); problemă de rezolvat: mijloacele laturilor unui patrulater convex sunt vârfurile unui paralelogram; umblu printre bănci şi observ ce fac elevii mei: desenează câte o figură, pe caietele "de matematică" standard (altfel… afară e soare şi linişte de vară târzie). Majoritatea ghidează rigla pe liniile caroiajului specific acestor caiete şi poate n-ar fi de mirare, că "patrulaterul" rezultă dreptunghiular; eu totuşi mă mir, aşa că scot la tablă pe cineva şi-i cer: desenează un patrulater; tabla este una obişnuită, necaroiată (spre deosebire de "caietul de matematică"), dar n-am noroc: elevul respectiv trasează fără să stea pe gânduri ceva care seamănă cu un pătrat (desigur, încep să înţeleg cam ce va fi de făcut cu elevii mei). N-am noroc, dar să luăm lucrurile aşa cum sunt şi cu calm: Bine dragă, Poftim la loc! Aleg un alt elev care şi el a trasat "figura" după liniile caietului, îl invit la tablă (după ce am şters-o) şi-i cer la fel: "desenează un patrulater"; ei… am noroc: parcă stă puţin pe gânduri, apoi trasează ceva care seamănă a dreptunghi.

Şi tot aşa… Susţin că după un anumit număr de astfel de încercări liniştite - fără comentarii şi fără trimiteri - vom avea pe tablă (dacă nu va fi sunat de ieşire, între timp) ceva care seamănă cu un "patrulater oarecare"; un asemenea experiment cu clasa poate fi mai valoros pentru lămurirea lăuntrică a elevilor de faţă, decât vreo scurtare prin expunerea directă şi impersonală a definiţiilor şi distincţiilor necesare (anterior, dobândisem deja un alt câştig important: am învăţat că e riscant să invoci "s-a făcut şi în clasele anterioare"; cerând explicaţii verbale pentru o noţiune sau alta, obţii unele formulări "pe dinafară", străine şi stâlcite - încât eşti obligat la "divagaţii" asupra folosirii corecte a termenilor şi a limbii, de către unul sau altul).

Cu oleacă de inspiraţie, asumând riscul de a încurca lucrurile în mintea unora, am modifica puţin derularea experimentului: Am văzut că ştiţi să desenaţi un pătrat, bravo! Desenaţi uşor (cu linie subţire) un pătrat (ceva mai mare) şi bifaţi câte un punct pe fiecare latură (chiar că nu ai noroc, dacă fiecare va bifa exact mijlocul laturii…); apoi trasaţi segmentele care unesc câte un punct cu punctul bifat pe latura vecină. Cum numiţi figura construită astfel? (să sperăm că "patrulater")

S-ar zice că aşa (chiar şi la acest nivel, vizat prin "evaluarea naţională"), începem cumva să facem matematică, adică să vedem şi chiar să construim relaţii, nuanţe, întrebări şi legături între fel de fel de lucruri; îmi imaginez ce ar zice inspectorul şcolar, ascuns undeva prin clasă ("scopul lecţiei era rezolvare de probleme, ori mata în loc să rezolvi, divaghezi şi nu ajungi să rezolvi nici măcar una")… dar aş continua cu întrebările mele: ce ziceţi despre patrulaterul rezultat, faţă de pătratul de la care aţi plecat? Dar oare, orice patrulater s-ar putea obţine plecând ca mai sus de la un pătrat? adică, orice patrulater poate fi înscris într-un pătrat? Şi poate aş propune ca "temă": construiţi un pătrat ale cărui laturi să treacă prin câte unul dintre vârfurile unui dreptunghi dat (dar puteţi face şi numai încercări: încercaţi întâi ca la tablă, "cu mâna liberă"; încercaţi pentru cazul când dreptunghiul dat este el însuşi, un pătrat).

Nu mai apucăm în cadrul acestei "lecţii", să atacăm "problema de rezolvat" enunţată la început; dar să observăm acum, că ea revine cumva la această formulare: în orice patrulater convex se poate înscrie un paralelogram (dar este unic? - adică, nu există şi vreun altul, diferit de cel definit de mijloace?).

Să mai observăm "iubite cetitorule", că totul – şi lecţiile noastre (inclusiv ghilimele, sublinieri, paranteze şi mai general, subânţelesurile) şi câştigurile fiecăruia şi încercările asumate de ambele părţi – totul depinde cumva (şi foarte dinamic) de noroc… Să mai observăm o posibilă dilemă: ce facem noi aici, matematică sau desen?! (facem şi una şi alta, că "Desen" s-a făcut în clasele anterioare…)

Chestiuni de înscriere

Într-un cerc sau într-un pătrat dat, se pot înscrie pătrate: în cazul cercului, capetele oricăror doi diametri perpendiculari determină un pătrat (iar în cazul unui pătrat, mijloacele laturilor acestuia determină un pătrat). Problema înscrierii unui pătrat se poate pune mai general (Otto Toeplitz, 1911): oare pe orice curbă simplă închisă din plan, se pot găsi patru puncte care să fie vârfurile unui pătrat? S-a demonstrat că răspunsul este afirmativ pentru unele categorii de curbe închise; de exemplu, într-un oval se poate înscrie totdeauna, un pătrat ("oval" fiind o curbă plană închisă convexă, cum ar fi de exemplu conturul plan al unui ou de găină, sau o elipsă).

Obs. Cercetările asupra conjecturii lui Toeplitz au vizat totdeauna pătratul, nu vreun poligon regulat "mai mare" - fiindcă între timp s-a reuşit (plecând de la triunghiul lui Reuleaux, în care se poate înscrie un poligon regulat doar cu 3, 4 sau 6 vârfuri) "construcţia" unei curbe simple închise cu proprietatea că oricare cel puţin 5 puncte ale sale nu formează un poligon regulat.

În particular, s-a evidenţiat că: orice patrulater se poate înscrie într-un pătrat (mai precis, pentru orice patrulater dat, există cel puţin un pătrat ale cărui laturi conţin câte un vârf al patrulaterului respectiv). Şi "invers": în orice patrulater dat se poate înscrie un pătrat (adică se pot alege patru puncte distincte, câte unul pe fiecare latură a patrulaterului dat, încât acestea să fie vârfurile unui pătrat).

Demonstraţiile acestor proprietăţi nu sunt "elementare" - dar ar fi de văzut sau de răsfoit [*] THE DISCRETE SQUARE PEG PROBLEM (Igor Pak, 2008), unde se prezintă două demonstraţii mai mult sau mai puţin elementare, a faptului că "Every simple polygon on a plane has an inscribed square". Rezolvăm totuşi (după o idee din [*]) un caz mai simplu: să arătăm că pe orice patrulater convex putem determina un triunghi echilateral înscris.

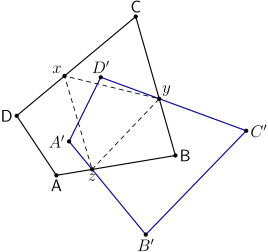Alegem un punct $z$ pe o latură a patrulaterului dat $\small\mathsf{ABCD}$. Rotim patrulaterul în jurul lui $z$ în sens orar cu $60^\circ$ şi fie $y$ un al doilea punct comun celor două patrulatere (să acceptăm că există $y$).
Rotind $y$ în sens antiorar cu $60^\circ$ în jurul lui $z$, găsim preimaginea lui $y$ prin prima rotaţie, deci un punct $x$ aflat pe patrulaterul iniţial.
Rezultă imediat că $xyz$ este un triunghi echilateral. Este clar deasemenea, că avem mai multe soluţii, depinzând de alegerea punctului iniţial $z$.

Se pare că putem adapta această idee pentru cazul mai general: există un triunghi $xyz$ înscris în patrulaterul $\small\mathsf{ABCD}$ care să fie asemenea unui triunghi dat? Înlocuim rotaţia cu $60^\circ$ din construcţia de mai sus cu rotaţia de unghi $\alpha$, unde $\alpha$ şi $\beta$ sunt două unghiuri ale triunghiului dat; găsim astfel un triunghi iniţial $xyz$ înscris în $\small\mathsf{ABCD}$, care are $\measuredangle{xzy}=\alpha$ (şi laturile din $z$ sunt - deocamdată - egale). Când am roti triunghiul $xyz$ în jurul lui $z$, punctele $y$ şi $x$ s-ar deplasa continuu pe laturile patrulaterului, iar unghiurile din $y$ şi din $z$ ar varia continuu - încât trebuie să existe o astfel de rotaţie prin care unghiul din $y$ să ajungă la valoarea $\beta$ (şi atunci obţinem $xyz$ asemenea triunghiului dat. Rămân totuşi de lămurit, aspectele de continuitate invocate aici după [*]).

Dar cum construieşti? Desigur, cu MetaPost

În loc de a lucra cu creta pe tabla obişnuită, folosim fără îndoială programe de "geometrie interactivă", ca GeoGebra (disponibil şi fără restricţii comerciale); interfaţa grafică respectivă oferă meniuri şi butoane adecvate pentru a instanţia pe ecran (folosind mouse-ul) puncte, linii, poligoane, cercuri, etc. şi pentru operaţii specifice de editare: etichetarea punctelor, liniilor, etc.; selectarea şi transformarea (translatare, dilatare, rotire, etc.) unui grup de obiecte de pe ecran; posibilităţi de "animare"; salvarea figurii într-un fişier de un anumit tip.

GeoGebra este un instrument foarte potrivit pentru lucrul în clasă, servind ca suport vizual (cu valenţe net superioare tablei clasice) pentru prezentarea orală şi pentru discuţia cu elevii a unor probleme de geometrie. Dar dacă ar fi vorba de a scrie ceva articol, ambalând enunţuri, figuri şi demonstraţii? Ideea de a scrie "interactiv" (cu Microsoft-Word şi de exemplu, Geogebra) este deja desuetă - cam peste tot astăzi, pentru scrierea articolelor ştiinţifice se foloseşte sistemul de tipografiere "TeX" pus la punct prin 1980 de către Donald Knuth. Sistemul LaTeX este încorporat de obicei în distribuţiile de Linux (fiind adaptat şi pentru instalare pe o platformă Microsoft-Windows), iar LaTeX oferă toate instrumentele care ar fi necesare cuiva pentru a scrie un articol ştiinţific (de matematică, de chimie sau electronică, sau poftim - de teorie muzicală, sau fie şi de şah), care să arate foarte bine când este tipărit, sau când este vizualizat pe ecran.

N-am nevoie să instalez şi să folosesc dinafara propriului sistem, nici ceva ca Word (sau "Office"), nici ceva ca GeoGebra; pentru a scrie articolul respectiv am nevoie de un editor decent de text ("gedit" încorporat de obicei în Linux este excelent) şi de un "terminal" - linia de comandă oferită îmi permite să lansez compilatorul de fişier LaTeX, compilatorul fişierului text în care am descris figurile, etc.

Lucrul în GeoGebra (sau alt software de "geometrie interactivă") se bazează pe construcţia vizuală a figurii, imitând foarte bine maniera în care ai desena-o cu creta la tablă. În schimb, construcţia unei figuri folosind MetaFont sau MetaPost (care sunt componente ale sistemului TeX) necesită descrierea textuală a construcţiei respective, utilizând fireşte anumite elemente de limbaj specific şi o anumită metodologie de transformare în final a descrierii respective, în imagine grafică.

Redăm aici o imagine din Michael de Villiers/Dynamic Math Learning, conţinând enunţul unei probleme de geometrie şi figura asociată acesteia, construită fie cu Geogebra, fie cu Sketchpad (pe pagina de pe care am preluat imaginea se oferă link-uri pentru "a FREE DEMO copy of SKETCHPAD", precum şi "To order a full version of Sketchpad in Southern Africa"):

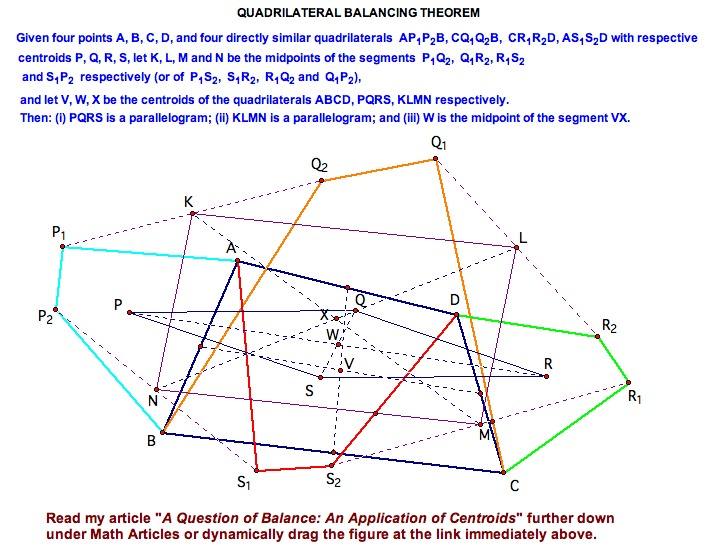
Sketchpad este destinat sistemelor Windows, dar văzând câteva demonstraţii pe YouTube pot zice şi eu că este un produs excelent, pentru studierea interactivă şi dinamică a diverse chestiuni de geometrie, algebră, sau de analiză matematică elementară; conţine aplicaţii separate după nivel (sau vârstă), cu licenţe valabile începând de la un an (până la "unlimited") şi de la "per computer" (până la 25, sau 100), costând (aproximativ) de la 5 dolari până la 60 şi 100 dolari, fiecare.

Ne propunem să construim folosind MetaPost, o figură corespunzătoare teoremei enunţate în imaginea de mai sus.

Bineînţeles că întâi am creat un director de lucru căruia să-i zicem şi noi, "DEMO/" şi în care am înscris un fişier "demo.mp" (în care urmează să descriem figura); apoi am deschis acest fişier în "gedit" şi deocamdată configurăm aici câteva aspecte:

%% demo.mp %%
outputformat := "png";
outputtemplate := "%j-%c.png";  % figura 99 va fi în fişierul "demo-99.png"
outputformatoptions := "format=rgba antialias=good";
verbatimtex  % contextele btex .. etex vor fi transferate compilatorului de (La)TeX
    \documentclass[12pt]{article}
    \begin{document}
etex

%% descrieri de figuri %% (secvenţe beginfig .. endfig)

end   % semnalează compilatorului că nu mai sunt alte figuri

Mai întâi, am schiţat cu creionul pe hârtie caroiată un patrulater, căutând să-l lipsim de particularităţi (evitând laturi paralele, egale, sau perpendiculare, unghiuri suplementare şi diagonale perpendiculare). Adăugăm în "demo.mp" descrierea corespunzătoare desenului meu (împreună aici cu o secvenţă de testare a figurii):

vardef ABCD =
    save z; pair z[];
    z1 = (0u, 0u); z2 = (6.5u, -0.5u); z3 = (4.5u, 3.5u); z4 = (1.5u, 3.5u);
    z1 -- z2 -- z3 -- z4 -- cycle
enddef;  % 'u' este unitatea de măsură din momentul instanţierii acestei definiţii

beginfig(99);
    save u; u = 1cm;  % unitatea de măsură curentă
    path p; p = ABCD;  % variabila 'p' înregistrează conturul patrulaterului
    draw p withpen pencircle scaled 1;
    %% etichetarea punctelor; adăugiri (diagonale, etc.) %%
endfig;

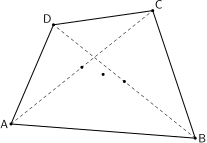
Marcarea şi etichetarea punctelor se poate face prin dotlabel.lft(btex $A$ etex, point 0 of p);, ş.a.m.d. (probabil că trebuie să stăpâneşti foarte bine limbajele (şi conceptele) TeX, ca să reuşeşti să formulezi o "funcţie generală" de etichetare, pe care s-o poţi invoca pentru un grup sau altul de puncte, în loc de a folosi câte o comandă pentru fiecare punct). Dacă apoi, lansăm compilatorul de MetaPost tastând pe linia de comandă a unui terminal mpost -tex=latex demo.mp, vom obţine ca rezultat al compilării fişierul "demo-99.png", redat în imaginea alăturată aici (a observa că în plus, am marcat mijloacele diagonalelor şi centroidul patrulaterului, urmărind să ne asigurăm că patrulaterul $\small\mathsf{ABCD}$ definit mai sus nu are aspecte particulare); desigur, am ales "99" ca index al figurii respective fiindcă ea a fost constituită doar în vederea unei testări ad-hoc - putem de-acum să eliminăm (sau "comentăm") definiţia respectivă din "demo.mp".

Pentru a modela teorema lui de Villiers ("quadrilateral balancing theorem"), vom avea nevoie să definim un alt patrulater, pentru a-l plasa printr-o anumită asemănare directă, pe fiecare latură a lui $\small\mathsf{ABCD}$; bineînţeles că ne-ar conveni să-l generăm aleatoriu - dar aceasta nu este aşa de uşor de realizat, trebuind să verificăm pe parcursul generării evitarea unor poziţii particulare. Deocamdată, ca urmare iarăşi a unor încercări manuale, optăm pentru această definiţie simplă (practic, am copiat definiţia "ABCD" şi am modificat punctele):

vardef XYZT =
    save z; pair z[];
    z1 = (1.5u, 0u); z2 = (2.75u, 1.75u); z3 = (-2.5u, 1.5u); z4 = (-2.25u, 0.5u);
    z1 -- z2 -- z3 -- z4 -- cycle
enddef;

Furnizând definiţii distincte pentru cele două patrulatere (în loc de una singură, parametrizată astfel încât să producă unul sau altul dintre ele), le vom putea modifica ulterior independent una de alta.

Dar cum construim o asemănare?

O asemănare directă roteşte punctele (în jurul originii) cu un acelaşi unghi fixat în prealabil, scalează (faţă de origine) cu un acelaşi factor fixat şi translatează cu un acelaşi vector fixat; este deci o transformare de forma $T(z)=az+b,\,z\in\mathbb{C}$ unde $a,\,b\in\mathbb{C}$ sunt valori fixate (într-adevăr, înmulţirea cu $a$ roteşte $z$ cu unghiul $\mathrm{arg}(a)$ şi scalează cu factorul $|a|$, apoi adunarea cu $b$ asigură translaţia finală).

Dacă exprimăm prin părţile reale şi imaginare corespunzătoare, obţinem: $$\begin{array}{@{}cll} x'=\alpha x-\beta y + \gamma \\ y'=\beta x + \alpha y + \delta \\ \end{array}$$ unde $z=x+iy,\,z'=T(z)=x'+y'i,\,a=\alpha+i\beta,\,b=\gamma+i\delta$ ($\in\mathbb{C}$).
Avem deci această caracteristică (de care ne vom folosi în MetaPost, mai jos): coeficienţii lui $x$ şi respectiv $y$ din exprimarea lui $x'$ şi $y'$ sunt egali (acelaşi $\alpha$), respectiv diferă numai prin semn ($\beta$ şi $-\beta$); aşa fiind, va nevoie să mai indicăm imaginile a numai două puncte (nu trei, cum ar fi necesar pentru o transformare liniară generală) pentru a determina $T$.

MetaPost prevede tipul de date "transform", prin formule de genul celor de mai sus pentru $x'$ şi $y'$, dar mai generale - având coeficienţi arbitrari. Prin urmare, vom putea construi pe latura $\small\mathsf{AB}$ (de exemplu), un patrulater asemenea cu $\small\mathsf{XYZT}$, definind ca mai sus o transformare $T$ (dar care să respecte caracteristica evidenţiată mai sus) şi impunând doar condiţia ca $\small\mathsf{X}$ să fie transformat în $\small\mathsf{A}$, iar $\small\mathsf{Y}$ în $\small\mathsf{B}$ (celelalte două vârfuri vor fi atunci transformatele prin $T$ determinat astfel, ale punctelor $\small\mathsf{Z}$ şi $\small\mathsf{T}$).

Trebuie să fim atenţi la ordinea în care apar vârfurile în enunţul teoremei: "Given four points A, B, C, D, and four directly similar quadrilaterals AP₁P₂B, CQ₁Q₂B, CR₁R₂D, AS₁S₂D …". Am modelat patrulaterul (cum se obişnuieşte în MetaPost) ca variabilă de tip "path p" (mai zicem "contur"), iar vârfurile vor putea fi accesate ca variabile de tip "pair" prin construcţia specifică "point i of p", unde valorile 0..3 pentru variabila numerică "i" ne vor da vârfurile patrulaterului (în ordinea dată la definirea conturului respectiv).

Următoarea "funcţie" construieşte pe latura indicată prin parametrii "i" şi "j" a conturului "p", un contur care este direct asemenea cu "q":

vardef similar(expr i, j, p, q) = 
    transform T;  % transformare liniară, de determinat prin 3 condiţii
    xxpart T = yypart T;  % coeficienţii lui x şi y (=α), în relaţiile x' şi y'
    xypart T = - yxpart T;  % β şi -β (v. mai sus, exprimările x', y')
    pair v[], w[];  % "vârfurile" pe contururile p şi q
    v1 = point i of p; v2 = point j of p;
    w1 = point 0 of q; w2 = point 1 of q;  %% totdeauna, latura XY a lui q
    w1 transformed T = v1;  % T transformă X şi Y în punctele i şi j din p 
    w2 transformed T = v2;
    w3 = (point 2 of q) transformed T;  % imaginile vârfurilor Z, T din q
    w4 = (point 3 of q) transformed T;
    v1 -- v2 -- w3 -- w4 -- cycle  %% conturul T(q), direct asemenea cu q
enddef;

Definiţia "similar()" poate fi adaptată uşor pentru alte cazuri: eliminând "w4" rezultă triunghiuri asemenea unuia XYZ dat; adăugând un "w5" vom obţine pentagoane asemenea unuia XYZTU dat; etc. Am verificat că pentru triunghiuri asemenea (în loc de patrulatere) teorema rămâne valabilă (baricentrele formează un paralelogram).

Pentru patrulaterele respective ne vor interesa baricentrele lor:

vardef centroid(expr h) =
    (point 0 of h + point 1 of h + point 2 of h + point 3 of h)/4
enddef;

Acum putem construi figura din teorema lui de Villiers astfel:

beginfig(1);
    save u; u = 1cm;  % unitatea curentă de măsură
    path p, q, qab, qbc, qcd, qda;
    p = ABCD;  q = XYZT; 
    % construieşte pe laturile lui p contururi asemenea cu q
    qab = similar(0, 1, p, q);  qbc = similar(2, 1, p, q);
    qcd = similar(2, 3, p, q);  qda = similar(0, 3, p, q);
    drawoptions(withpen pencircle scaled 0.8);
    draw qab  withcolor 0.5black;
    draw qbc  withcolor red;
    draw qcd  withcolor blue;
    draw qda  withcolor green;
    pair c[];  % baricentrele patrulaterelor construite
    c1 = centroid(qab);  c2 = centroid(qbc);
    c3 = centroid(qcd);  c4 = centroid(qda);
    drawoptions(withpen pencircle scaled 4pt);
    drawdot c1 withcolor 0.5black;  drawdot c2 withcolor red;
    drawdot c3 withcolor blue;  drawdot c4 withcolor green;
    % paralelogramul baricentrelor
    draw c1 -- c2 -- c3 -- c4 -- cycle 
         withpen pencircle scaled 0.4 dashed evenly;
    % îngroaşă conturul ABCD (păstrând culorile patrulaterelor construite)
    drawoptions(withpen pencircle scaled 2);
    draw point 0 of p -- point 1 of p  withcolor 0.5black;
    draw point 1 of p -- point 2 of p  withcolor red;
    draw point 2 of p -- point 3 of p  withcolor blue;
    draw point 0 of p -- point 3 of p  withcolor green;
    drawoptions();
endfig;

Recuperând pe linia de comandă mpost -tex=latex demo.mp, obţinem "demo-1.png", reprezentând grafic figura creată mai sus (aici o redăm la 50% din mărimea reală):

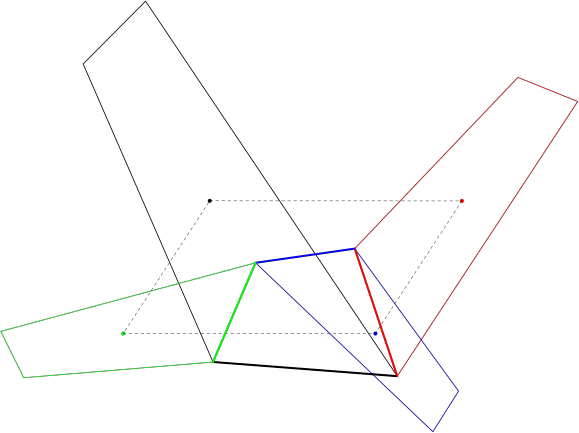
Am vizualizat doar partea esenţială a teoremei: baricentrele patrulaterelor direct asemenea construite pe laturile unui patrulater dat formează un paralelogram. Este mai puţin important (şi oricum, este banal) să completăm figura, adăugând notaţiile punctelor şi evidenţiind mijloacele de segmente şi celelalte paralelograme din enunţul complet al teoremei.

Dacă înlocuim definiţia "XYZT" astfel încât XYZT să fie un pătrat (reducând-o deci la vardef XYZT = unitsquare enddef; unde "unitsquare" este conturul pătrat centrat în origine cu latura 1bp, predefinit în fişierul macro-urilor de bază inclus automat de către compilator), atunci obţinem o construcţie analogă celeia din teorema lui Van Aubel:

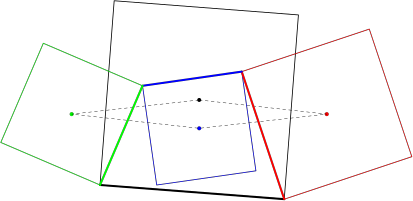
diferenţa fiind că acum, paralelogramul baricentrelor nu are diagonalele "egale şi perpendiculare" (ca în teorema lui Van Aubel, unde pătratele vizate erau toate spre exteriorul patrulaterului dat), ci doar "perpendiculare".