De la încadrarea profesorilor la orarul şcolii, folosind R
[1] Distribuţia orară a distribuţiei pe zile a orelor şcolii (I..III)
[2] Distribuţia pe zile a orelor dintr-o şcoală cu un singur schimb (I..V)
O încadrare cu clase partajate
Următorul tabel reprezintă încadrarea profesorilor dintr-o anumită şcoală (reală sau nu), în ordinea descrescătoare a numărului de ore pe săptămână:
10_________ 11_________ 12_________ 9__________ prof A B C D E F A B C D E F A B C D E F 5 6 7 8 A B C D E F P01 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 P02 5 3 . . . . 7 . . . . 1 3 1 . . . . 1 . . . 7 . . . . . P03 3 6 . 1 . . 3 . . 2 . . 7 . 2 . . . . 1 . . 3 . . . . . P04 . . 1 3 . . . . . 2 2 1 . 1 . 5 5 3 . . . . . . . 2 . 2 P05 . . 3 . 2 3 . 2 . . . . 2 2 . . 5 . . 2 . . 2 2 . 2 . . P06 . . 2 . 1 1 . 2 2 . 2 . . . . 1 1 1 . . 1 1 . 3 3 2 2 2 P07 . 4 . . . . . . . . . . 4 . . . 2 . . . 6 . . 4 4 . . 2 P08 . . 4 . . . 5 4 . . . . . 5 . . . . . . . 4 4 . . . . . P09 . 2 . . . . . . . 2 9 . . . . . . 4 2 . . 2 . . . . . 4 P10 1 1 1 1 1 1 . . . 1 1 1 . . . 1 1 2 1 1 1 1 1 1 1 1 1 2 P11 . . . 2 2 . . 3 . . . . . . 3 . . . . . . 2 . 3 4 2 . 2 P12 . 2 . 2 . . . 2 2 2 . . 2 . . 5 . . . . . . 2 . . 4 . . P13 2 . 2 . . 3 . . . . 2 3 . . . . . . 2 . 2 . . 2 2 . 2 . P14 2 . 3 . . . 1 4 3 . . . 1 . . . . . . . 2 2 2 . . 1 . 1 P15 . . . . 6 . 2 . . . 1 . . 2 2 . 2 3 . 2 . 2 . . . . . . P16 . . . 2 3 2 . . . 2 2 . . . 4 2 . . . . . . . . . 2 2 . P17 2 2 . . 1 . . 3 3 . . 1 1 . . . . 1 . . . . . 4 3 . . . P18 . . 3 . . . . . . . . . 4 . . . 4 . . . . 5 . . . . 5 . P19 2 . . . . . . . 1 2 1 2 2 . . . . 1 . . 2 2 1 1 1 . 1 1 P20 3 . . . . . . 4 . 5 . . . . . 4 . . . . . . . 4 . . . . P21 . 3 . . . . . . 4 . 4 . . . 4 . . . . . . . . . . 5 . . P22 . . . 4 . . . . . 4 . . 1 . . . 5 3 . . . . . . . . 2 . P23 . 2 2 1 1 1 1 1 . . . . . 1 1 1 1 . 3 2 . . . . . 1 . . P24 . . . . . . . . . . 4 . . . . 4 . . 2 2 . . 1 1 1 2 . 2 P25 . . . 4 . . . . . . . 6 . 4 . . . 5 . . . . . . . . . . P26 . . 2 1 . 1 1 . . . . . . 4 3 . . . . 2 . 1 2 . . 1 1 . P27 1 1 1 . 3 4 1 1 1 . . 3 . 1 1 . . . . . . . . . . . . . P28 1 1 1 2 . . 1 . . . . . 1 1 . 2 . . 1 . . 3 1 . . 2 . . P29 . 2 . 1 1 1 . . . . . . . 3 4 . . . . . . . . 2 2 . 1 . P30 . 3 3 . . 2 . . 4 . . . . 3 . . . . . . . . . . . . 2 . P31 1 1 1 1 1 1 . . . . . . . . . . . . 1 1 1 1 1 1 1 1 1 1 P32 2 . . . . . . . . . . . . . . . 6 . . . . . . . . . 6 . P33 . . . 3 . . . . 2 . . 3 . . 2 2 . . . . . . . . 2 . . . P34 . . . . . . . . . . . . . . . . . . . 5 . . . . 4 . . 4 P35 . . . . 4 4 4 . . . . . . . . . . . . . . . . . . . . . P36 3 . . . . . 3 . . . . . 3 . . . . . . . . . 3 . . . . . P37 . . . . . 2 . . . . 2 2 . . . . . . . . . . . . . . 2 2 P38 . . . 1 1 1 . . . . . 2 . . . . . 1 . . 1 . . . . 1 1 1 P39 . . . . . . 2 . . . . . . . . . . . . . 2 . . . . . 5 . P40 . . . . 2 . . . 1 . . . . . 1 . 2 . . . . . . 1 . . . 2 P41 . . . . . . . . 4 . . . . . . . . . 5 . . . . . . . . . P42 1 1 1 1 1 1 1 1 . . . . . . . . . . . . . . . . . . . . P43 . . . . . . . . . . . . . . . . . . . . 4 . 4 . . . . . P44 4 . . . . . . . . . . . . . . . . . . 4 . . . . . . . . P45 1 1 . . . . . . . . . . . . . . . . . . . . 1 1 1 . 2 . P46 . . . . . . . . 1 2 2 1 . . . . . . . . . 1 . . . . . . P47 . . . . . . . 1 . 3 . . . . . . . 2 . . . . . . 1 . . . P48 . . . . 6 . . . . . . . . . . . . . . . . . . . . . . . P49 . . . . . . . . . . 5 . . . . . . . . . . . . . . . . . P50 . . . . . . . . . . . . . . . . . . 1 . 2 . . . . . . 1 P51 . . . . . . . . . . . . . . . . . . . 2 2 . . . . . . . P52 . . . . 2 2 . . . . . . . . . . . . . . . . . . . . . . P53 . . . . . . . . . . . . . . . . . . 4 . . . . . . . . . P54 . . . . . . . . . 1 . 1 . . . 1 . 1 . . . . . . . . . . P55 . . . . . . . . . . . . . . . . . . . . 1 2 . . . . . . P56 . . . . . . . . . . . . . . . . . . 1 1 1 . . . . . . . P57 . . . . . . . . . . . . . . . . . . 1 . 1 1 . . . . . . P58 . . . . . . . . . . . . . . . . . . . 1 1 . . . . . . . P59 . . . . . . . . . . . 1 . . . . . 1 . . . . . . . . . . P60 . . . . . . . . . . . . 1 . 1 . . . . . . . . . . . . . P61 . . . . . . . . . . . . . . . . . . . 1 . . . . . . . . A B C D E F A B C D E F A B C D E F 5 6 7 8 A B C D E F 10 11 12 9
Întrebare: este vorba de o şcoală reală? Păi într-o încadrare inventată de noi, n-am fi considerat profesori cu o singură oră pe săptămână (ba chiar, nici cu numai două sau trei ore); în realitate, "P61" are 36 ore/an (şi numai orarul vede "1 ore/săpt.").
Este vorba de o şcoală reală, cu câte 6 clase pe nivelele 9..12 şi cu 4 clase gimnaziale 5..8; nu-i cazul să punem întrebări fără sens: care şcoală anume, de unde? sau, care este numele (şi CNP-ul) lui "P07"?
Întrebare: Ce disciplină predă P01? Păi "P01" are câte o oră la fiecare clasă (şi una în plus la 10A) – deci predă "Religie" (singurul obiect impus politic la toate clasele). Disciplinele nu sunt precizate, dar ele sunt totuşi importante pentru a reda complet orarul şcolar.
Întrebare: cum de "P09" are 9 ore, la clasa 11E? Întrebarea are sens: există numai trei profesori cu mai mult de 6 ore la o aceeaşi clasă (şi numai 7 cazuri cu 6 ore). "P02" şi "P03" au 7 sau 3 ore la aceleaşi clase (şi 5/3 sau 3/6 la 10A şi 10B); de obicei (într-o şcoală reală) clasele "A" sunt „de informatică”, iar parte dintre orele de "Info" se desfăşoară partajând clasa între doi profesori; la fel stau lucrurile pentru alte câteva discipline (de obicei, limbi străine, sau "Des/Muz") şi probabil, cele 9 ore la 11E sunt partajate cumva între "P09" şi alţi profesori.
Pe tabelul de încadrare de mai sus (extras din orarul public al unei anumite şcoli) sunt înregistrate toate orele profesorilor, indiferent de faptul că unele dintre acestea sunt ore comune mai multor profesori (de obicei, doi profesori care partajează o clasă într-o aceeaşi oră a zilei); „orarul claselor” (publicat separat de „orarul profesorilor”) ne-a furnizat informaţiile privitoare la partajarea claselor.
Reluăm din [1], repartizarea pe zile şi pe orele zilei a orelor din încadrare – îmbunătăţind într-o anumită măsură programele respective şi ţinând seama acum şi de situaţiile în care doi profesori trebuie să intre simultan la o aceeaşi clasă.
Introducerea cuplurilor prin „profesori fictivi”
Extindem tabelul de încadrare de mai sus cu o listă de profesori fictivi, reprezentând fiecare câte un cuplu de profesori care partajează anumite clase:
prF <- list(F1 = c("P02", "P03"), F2 = c("P31", "P10"), F3 = c("P32", "P39"), F4 = c("P32", "P05"), F5 = c("P09", "P13"), F6 = c("P09", "P15"))
"P02" şi "P03" partajează pe câte 3 ore, fiecare dintre clasele 10A, 10B, 11A, 12A şi 9A; scădem câte 3 ore fiecăruia, la clasele respective, punându-le în schimb la "F1":
10_________ 11_________ 12_________ 9__________
prof A B C D E F A B C D E F A B C D E F 5 6 7 8 A B C D E F
P02 2 0 . . . . 4 . . . . 1 0 1 . . . . 1 . . . 4 . . . . .
P03 0 3 . 1 . . 0 . . 2 . . 4 . 2 . . . . 1 . . 0 . . . . .
F1 3 3 . . . . 3 . . . . . 3 . . . . . . . . . 3 . . . . .
La alocarea pe zile, va trebui să avem grijă ca în fiecare zi, suma dintre numărul de ore „fictive” (alocate lui "F1") şi numărul de ore alocate lui "P02", respectiv lui "P03", să fie în ambele cazuri cel mult 7. La alocarea pe orele zilei, va trebui să avem grijă ca orele din zi alocate lui "F1" să nu se suprapună nici cu orele lui "P02", nici cu orele lui "P03" (încât aceştia să poată intra împreună în acea zi, la clasele respective).
La fel avem de revizuit tabelul de încadrare, pentru integrarea celorlalţi profesori fictivi din lista prF. Pentru unele partaje existente în contextul real din care am extras datele de mai sus, n-a fost necesar să înfiinţăm vreun profesor fictiv; de exemplu, "P15" şi "P48" sunt cuplaţi pe clasa 10E, cu câte 6 ore – dar "P48" apare în tabelul de încadrare de mai sus numai cu această clasă, încât devine suficient să eliminăm pur şi simplu "P48" (şi numai la afişarea orarului final, să ţinem seama cumva de faptul că orele lui "P15" la 10E trebuie notate fiecare şi cu "P48").
După ce am modificat astfel tabelul de încadrare, am înlocuit pe toate rândurile " " cu "," (şi '0' cu '.') – obţinând încadrarea în format CSV, "incadrare.csv".
Normalizarea datelor de încadrare
Pentru a folosi algoritmii de etichetare (cu zile, respectiv cu ore-ale-zilei) din [1], trebuie să aducem încadrarea la „forma normală” (specificând orele din încadrare prin linii 'prof' | 'clasă', repetate consecutiv de câte ore are 'prof' la 'clasă'):
fram <- read_csv("incadrare.csv", na = '.') %>% # sum(!is.na(fram[, 2:29])) ## 409 gather("cls", "nore", 2:29) %>% filter(! is.na(nore)) %>% # 409 linii 'prof' | 'cls' | 'nore' mutate(nore = as.integer(nore)) %>% # sum(fram$nore) ## 839 uncount(nore) # 'prof' | 'cls' (cu linii identice de câte 'nore' ori) > str(fram) # inspectează structura datelor, din consolă tibble [839 × 2] (S3: tbl_df/tbl/data.frame) $ prof: chr [1:839] "P01" "P01" "P02" "P02" ... $ cls : chr [1:839] "10A" "10A" "10A" "10A" ...
Transformăm coloana $prof în factor, ordonat descrescător după numărul de ore pe săptămână corespunzător profesorului:
srt <- sort(table(fram$prof), decreasing=TRUE) fram$prof <- factor(fram$prof, levels = names(srt), ordered=TRUE) > str(fram) tibble [839 × 2] (S3: tbl_df/tbl/data.frame) $ prof: Ord.factor w/ 65 levels "P01"<"P04"<"P06"<..: 1 1 31 31 28 28 28 10 10 13 ... $ cls : chr [1:839] "10A" "10A" "10A" "10A" ...
Cu table() putem vedea 'fram' din nou ca „tabel de încadrare” (în forma iniţială, având coloane pentru fiecare clasă) şi prin apply() putem aplica sum() pe liniile tabelului, obţinând numărul total de ore pentru fiecare profesor:
> apply(table(fram[c('prof','cls')]), 1, sum) P01 P04 P06 P07 P08 P11 P12 P05 P09 P14 P15 P16 P17 P18 P13 P19 P20 P21 P22 P23 29 27 27 26 26 23 23 22 22 22 21 21 21 21 20 20 20 20 19 19 P24 P25 P26 P27 P28 P29 P30 F1 P10 P33 P02 P03 P34 P35 P36 P37 P38 F2 P40 P41 19 19 19 18 17 17 17 15 15 14 13 13 13 12 12 10 10 9 9 9 P42 P43 P44 P31 P45 P46 P47 F4 F3 P32 P39 P50 P51 P52 P53 P54 P55 P56 P57 F5 8 8 8 7 7 7 7 6 5 4 4 4 4 4 4 4 3 3 3 2 P58 P59 P60 F6 P61 2 2 2 1 1
Din rezultatul redat deducem că primii 37 profesori (dinaintea lui "F2") au fiecare cel puţin 10 ore pe săptămână; când vom repartiza pe zilele de lucru cele 839 de ore din încadrare, vom cere ca orele acestora să fie distribuite cât mai uniform (v. [2]).
Am zice că această încadrare este mai densă decât cea vizată în [1], media orară fiind 839/65≈13 ore de profesor, pe 28 de clase – faţă de [1], unde aveam 1202/76≈16 ore de profesor pe 41 de clase (iar 13/28 > 16/41); vom vedea mai încolo că densitatea încadrării este importantă (programul de repartizare pe orele zilei din [1] trebuie corectat, pentru a nu eşua dacă încadrarea este prea densă).
Deocamdată, folosind saveRDS(), salvăm datele respective în fişierul frame.RDS.
Repartizarea pe zile a încadrării
Reluăm cu anumite îmbunătăţiri şi corecturi, programul "distribute.R" din [2].
Anterior, în funcţia CND() se opera pe toate coloanele matricelor de alocare (curentă şi respectiv, cumulată) – acum operăm numai pe acele coloane care corespund profesorilor clasei curente (prevăzând în prealabil lista prOf – care indică profesorii fiecărei clase în parte – şi desemnând coloanele lui Zore prin levels(FRM$prof)).
În [2] adăugam coloana $zl (în cadrul funcţiei alloc_by_class()) ca factor ordonat, folosind gl(); dar este suficient să folosim rep_len(1:5, nrow(.)) (etichetând zilele prin 1..5 şi repetând secvenţa pe toate orele clasei curente) şi abia în final, să convertim $zl în factor cu nivelele Zile ("Lu", "Ma", etc.).
Bineînţeles că prin aceasta, viteza de execuţie sporeşte sensibil. Dar am evitat să mai complic în CND(), condiţiile impuse distribuţiilor individuale; este mult mai simplu de rezolvat interactiv (ulterior obţinerii rezultatului programului) diversele situaţii particulare (de exemplu, cazul când lui "F1" i s-au alocat 4 ore, în timp ce "P02" are deja 4 ore – însemnând că în ziua respectivă "P02" ar avea 8 ore, în loc de maximum 7).
# distribute_by_days.R (distribuie pe zile, orele din încadrarea profesorilor) library(tidyverse) FRM <- readRDS("frame.RDS") # 839 linii <prof> <cls> (fiecare oră din săptămână) nrPr <- nlevels(FRM$prof) # 65 profesori; primii 37 au măcar 10 ore pe săptămână FRM <- FRM %>% split(.$cls) # listă de „tabele”, câte unul de clasă prOf <- map(FRM, function(K) { # lista profesorilor fiecărei clase lpr <- unique(K$prof) lpr[lpr < "F2"] # restrânge lista la cei cu măcar 10 ore/săpt. }) # alocă orele pe zile, pentru fiecare clasă alloc_by_class <- function() { # matricea de control a numărului de ore pe zi cumulat, la profesori Zore <- matrix(data=rep(0L, 5*nrPr), nrow = 5, ncol = nrPr, byrow=TRUE, dimnames = list(1:5, levels(FRM$prof))) # Condiţiile impuse unei distribuţii pe zile a orelor CND <- function(More, lpr) { # 'lpr' = lista profesorilor clasei mex <- Zore[, lpr] + More[, lpr] # cumulează alocările, curentă şi anterioară for(j in 1:ncol(mex)) { Pr <- mex[, j] # câte ore ar avea, în fiecare zi, profesorul for(oz in Pr) if(any(abs(Pr - oz) > 2)) return(FALSE) # refuză alocarea, dacă nu este "pseudo-omogenă" } return(TRUE) # acceptă alocarea: nr. ore/zi variază cu max. 2 } # montează coloana zilelor alocate orelor unei clase labelsToClass <- function(Q) { # 'Q' conţine liniile din FRM cu o aceeaşi 'cls' lpr <- prOf[[Q$cls[1]]] # profesorii clasei (cu măcar 10 ore/săpt.) S <- Q %>% mutate(zl = rep_len(1:5, nrow(.))) # verifică dacă orele pe zi alocate curent respectă CND() more <- t(as.matrix(table(S[c('prof', 'zl')]))) if(CND(more, lpr)) { Zore <<- Zore + more # actualizează numărul de ore pe zi return(S) # o distribuţie care îndeplineşte condiţiile } # dacă nu-s îndeplinite CND(), permută profesorii clasei şi reia Q <- Q %>% arrange(match(prof, sample(unique(prof))), prof) return(labelsToClass(Q)) # Reia dacă nu-s îndeplinite condiţiile } # (programul va fi stopat dacă reapelarea nu mai este posibilă) tryCatch( # previne stoparea programului (v. [1]) { FRM %>% # etichetează liniile fiecăreia dintre clase map_df(., function(K) labelsToClass(K)) }, error = function(err) { # s-a depăşit capacitatea stivei de apeluri FRM <- FRM %>% sample(.) # permută grupurile de linii ale claselor tryCatch({ cat("1") ## vizualizează cumva, reluările alloc_by_class() # reia, în noua ordine de clase }, error = function(e) NULL ) } ) # Returnează distribuţia pe zile a orelor claselor indicate (sau NULL) } # încheie 'alloc_by_class()' Dis <- alloc_by_class() Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") Dis <- Dis %>% mutate(zl = factor(zl, labels=Zile)) saveRDS(Dis, file = "byDays1.rds") # 'byDays2.rds', 'byDays91.rds', etc. # afişează distribuţiile individuale pentru orele profesorilor print(addmargins(as.matrix(table(Dis[c('prof', 'zl')])))) # dacă 'Dis' ≠ NULL
Numai în două din vreo zece execuţii, am obţinut ca rezultat NULL: funcţia alloc_by_class() n-a reuşit – autoapelându-se (în limitele stivei de apeluri) cu o ordine schimbată aleatoriu a claselor şi a profesorilor clasei – să ajungă la o distribuire a orelor care să respecte CND(); altfel, distribuţia este produsă într-un timp mediu de 2 minute (pentru cazul de aici, cu 65 de profesori şi 28 de clase, totalizând 839 de ore).
Toate rezultatele Dis (din diversele execuţii ale programului de mai sus) au aceeaşi distribuţie (neuniformă) a numărului total de ore pe zi (descrescând în ordinea zilelor, după cum am justificat în [2]):
> unlist(lapply(Zile, function(z) nrow(Dis[Dis$zl == z, ]))) [1] 175 172 168 166 158 # Total: 839 ore
Urmează să revizuim interactiv una dintre distribuţiile pe zile rezultate, pentru a uniformiza numărul total de ore pe zi (ideal ar fi să avem o zi cu 167 de ore şi 4 zile cu câte 168 ore), pentru a remedia eventualele cazuri în care profesorii care partajează clase cumulează mai mult de 6-7 ore pe zi şi pentru a mai îndrepta alocarea orelor la profesorii cu puţine ore (evitând situaţia „o oră pe zi”).
Demersuri necesare finalizării distribuţiei pe zile
Prin următorul program modelăm una dintre distribuţiile pe zile obţinute mai sus, în formatul CSV cerut de aplicaţia /recast; deasemenea, extragem într-un fişier separat liniile corespunzătoare orelor cuplate prin „profesorii fictivi”, precum şi matricea care indică pentru fiecare clasă numărul de ore pe fiecare zi:
# disToRecast.R rm(list=ls()) library(tidyverse) D <- readRDS("byDays91.rds") # distribuţia pe zile (prof|cls|zl) a celor 839 de ore # listă de 5 obiecte 'tibble' (prof|cls), câte unul pentru fiecare zi lDz <- D %>% split(.$zl) %>% map(., function(z) z[, 1:2] %>% arrange(prof)) # modelează tabelul necesar aplicaţiei /Recast (scriindu-l apoi în format CSV) Drc <- data.frame(prof="", Lu="", Ma="", Mi="", Jo="", Vi="") row = 1 for(P in levels(D$prof)) { # prof Lu Ma Mi Jo Vi Drc[row, 1] <- P # P31 |6 7|9E| |5 8 9D|9F for(q in 2:6) { ql <- lDz[[q-1]] %>% filter(prof == P) Drc[row, q] <- paste(c(ql$cls), collapse=" ") } row <- row + 1 } write_csv(Drc, file="Dis91.csv") # Copy&Paste în aplicaţia interactivă /Recast # alocarea pe zile a orelor cuplate prin profesorii "fictivi" prF <- list(F1 = c("P02", "P03"), F2 = c("P31", "P10"), F3 = c("P32", "P39"), F4 = c("P32", "P05"), F5 = c("P09", "P13"), F6 = c("P09", "P15")) tgt <- paste0("F", 1:6) # cheile din lista 'prF' together <- map_df(tgt, function(key) Drc %>% filter(prof %in% c(key, prF[[key]])) %>% arrange(prof)) sink("together.txt") print(together, row.names=FALSE, width=150) print(addmargins(table(D[c('cls', 'zl')]))) # ore/zi pentru fiecare clasă sink()
Conţinutul fişierului "Dis91.csv" poate fi pastat ca atare în caseta iniţială a aplicaţiei /recast (sau, mai bine, direct în elementul <textarea> al fişierului-sursă "recast.html"); datele din fişierul "together.txt" ne servesc pentru a decide ce clase să mutăm (prin operaţia SWAP a aplicaţiei) dintr-o zi în alta, încât să echilibrăm zilele în privinţa numărului total de ore pe zi şi să corectăm eventualele neajunsuri privind alocarea pe zile a orelor cuplate.
De exemplu, pentru orele cuplate prin "F1" avem această situaţie:
prof Lu Ma Mi Jo Vi
F1 10A 10B 10A 10B 12A 9A 11A 12A 9A 11A 12A 9A 10A 10B 11A
P02 11A 9A 11A 5 9A 10A 11A 9A 10A 11F 12B 11A 9A
P03 12A 12C 10B 11D 12A 12C 10B 11D 10B 12A 10D 12A 6
În ziua Lu, profesorii "P02" şi "P03" au câte 4 ore, dintre care două împreună (la clasele 10A şi 10B, alocate fictiv lui "F1"); însă Ma, "P02" are 7 ore, iar "P03" are chiar 8 ore – ceea ce trebuie corectat: de exemplu, ar fi suficient să mutăm la "F1" clasa 12A din ziua Ma în ziua Lu şi la "P03", clasa 12C din ziua Ma în ziua Mi (astfel, "P02" şi "P03" nu vor avea zile cu mai mult de 6 ore, comune sau nu).
Finalizarea interactivă a distribuţiei pe zile
Mai întâi uniformizăm numărul total de ore pe zi, urmărind totodată ca profesorii cuplaţi să aibă cel mult 6 ore pe zi; operaţia Mark din /recast evidenţiază liniile profesorilor care au ore la clasa indicată şi este uşor să vedem la cine ar fi cel mai bine să mutăm (prin SWAP) clasa respectivă dintr-o zi în alta (şi eventual invers, din ziua-destinaţie înapoi în ziua-sursă). Mutând unele clase din zilele Lu şi Ma (în care aveau câte 7 ore) în ziua Vi, am ajuns uşor la o distribuţie uniformă (168 168 168 167 168), pentru numărul total de ore pe zi (iar profesorii cuplaţi au fiecare, cel mult 6 ore pe zi).
Încheind repede această primă etapă, am salvat rezultatul – folosind operaţia "Export" – amânând pentru mai târziu, diverse alte modificări; dar am constatat că în fişierul CSV furnizat, clasele nu sunt indicate corect – de exemplu avem:
P34,69F,69C,69C 9F,69C 9F,69C 9F # corect: P34,6 9F,6 9C,6 9C 9F,6 9C 9F,6 9C 9F
Citind handler-ul de click pentru link-ul Export (redat şi în [2](III)), se poate deduce uşor de ce clasele 5..8 (notate cu câte o cifră) nu sunt redate corect: prin qls = $(el).text() extrăgeam textul conţinut de elementul <td> curent, obţinând de exemplu qls = "10A10B12B69A", sau pentru linia exemplificată mai sus qls = "69F"; apoi separam clasele din şirul qls folosind qls = qls.match(/\d*[A-Z]/g) – ceea ce ar fi corect dacă fiecare clasă este notată (ca de obicei) prin "cifre + literă".
De corectat, n-ar fi o problemă: de exemplu, putem folosi (cam grosolan) .match(/9[A-Z]|10[A-Z]|11[A-Z]|12[A-Z]|5|6|7|8/g), identificând separat fiecare clasă, fie că este notată obişnuit, fie că este notată 5..8 (fără literă). Numai că, modificând acum codul javaScript şi reîncărcând apoi în browser fişierul "recast.html" – am reveni la distribuţia iniţială, pierzând modificările făcute deja asupra acesteia…
A fost un bun prilej de a observa că în Firefox nu mai avem (ca acum câţiva ani) un meniu "View Generated source", dar şi o ocazie de a înţelege că acesta nici nu este necesar: utilizăm instrumentul "Inspector" (accesibil de exemplu prin combinaţia de taste Ctrl+Shift+C), selectăm <div>-ul care conţine tabelul HTML redat la momentul respectiv în fereastra browser-ului şi din meniul deschis prin click-dreapta alegem "Copy / InnerHTML" – obţinând fragmentul HTML corespunzător tabelului respectiv. L-am pastat apoi într-o copie „curată” a fişierului "recast.html" (fără elementul <textarea> şi fără activarea widget-ului .recast()) şi am imitat operaţia "Export", adăugând un element <a> împreună cu un <script> conţinând handler-ul de click corespunzător (modificând acum, expresia din .match(), cum am arătat mai sus).
Am reuşit astfel să obţin fişierul CSV corect, reflectând modificările întreprinse asupra distribuţiei iniţiale; bineînţeles că l-am pastat în elementul <textarea> din fişierul recast.html, încât la următoarea lansare a aplicaţiei vom putea continua modificările, în loc să o luăm de la capăt.
De notat şi „lecţia” primită: este bine să notăm clasele în modul obişnuit, sau în orice caz într-un acelaşi stil (deci "5A" şi nu "5")…
Ilustrăm genul de modificări care ar mai fi de făcut, pentru a îmbunătăţi unele distribuţii individuale. La clasa 10F avem câteva cazuri de „o oră pe zi”:
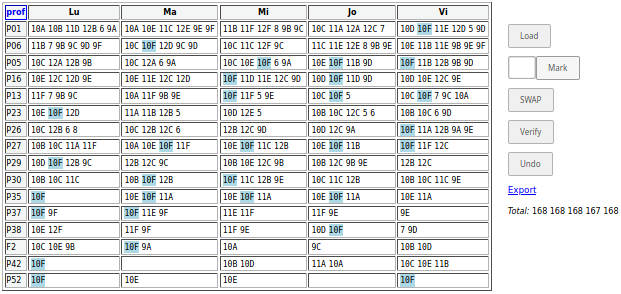
"P52" are numai 4 ore pe săptămână şi le-ar face în 4 zile (câte una pe zi); de dorit ar fi să le facă în 2 zile, iar o posibilitate de redistribuire constă în următoarea secvenţă de operaţii SWAP:
P52: 10F (Vi) --> Ma Ma: 10E 10F P37: 10F (Ma) --> Vi Ma: 11E 9F Vi: 9E 10F P52: 10F (Lu) --> Mi Mi: 10E 10F P30: 10F (Mi) --> Lu Lu: 10B 10C 11C 10F Mi: 11C 12B 9E
Astfel, distribuţia iniţială pentru "P52" (1 1 1 0 1) a devenit (0 2 2 0 0); cea iniţială pentru "P37" (2 3 2 2 1) a devenit omogenă, (2 2 2 2 2); iar cea pentru "P30" nu şi-a pierdut caracterul de omogenitate (2 zile cu câte 4 ore şi 3 zile cu câte 3 ore).
Desigur, am ţinut seama de faptul că 10F intră într-un cuplaj (fiindcă apare la "F2"), dar acest cuplaj nu angajează niciunul dintre cei 3 profesori implicaţi în operaţiile SWAP redate mai sus.
După ce am făcut o serie de asemenea modificări (dar numai dintre cele mai evidente), am salvat distribuţia obţinută în fişierul divRecast.csv; urmează să generăm orarele fiecărei zile. Subliniem că nu ne-am ocupat mai mult de vreo 20-30 de minute, să redistribuim orele pe zile prin /recast; probabil că ocupându-ne mai mult, am putea obţine o distribuţie pe zile chiar „perfectă” – numai că experienţa cumulată anterior în [1] şi [2] sugerează că tocmai în acest caz, reducerea numărului de ferestre pe orarele zilnice devine dificilă.
Probabil că planul de lucru cel mai bun este acesta: facem prin aplicaţia /recast numai modificările „evidente”, precum cele ilustrate mai sus; apoi producem orarele zilnice şi deducem eventual ce modificări în repartiţia pe zile divRecast.csv ar mai fi de făcut, încât să putem reduce cât mai mult numărul ferestrelor apărute pe orare; dacă este cazul, putem relua /recast, modificând divRecast.csv (acum, în cunoştinţă de cauză) şi apoi, generând din nou orarele, pentru noua distribuţie pe zile a orelor.
Renormalizarea datelor (din distribuţia CSV pe zile)
Redăm fişierul divRecast.csv (separând însă unele linii prea lungi):
prof,Lu,Ma,Mi,Jo,Vi
P01,10A 10B 11D 12B 6 9A,10A 10E 11C 12E 9E 9F,11B 11F 12F 8 9B 9C,
10C 11A 12A 12C 7,10D 10F 11E 12D 5 9D
P04,10D 12D 12E 12F 9D 9F,10D 12B 12D 12E 12F 9D,10D 12D 12E 12F,
11D 11E 11F 12D 12E,10C 11D 11E 12D 12E 9F
P06,11B 7 9B 9C 9D 9F,10C 10F 12D 9C 9D,10C 11C 12F 9C,11C 11E 12E 8 9B 9E,
10E 11B 11E 9B 9E 9F
P07,10B 12A 12E 7,12A 7 9B 9C 9F,10B 7 7 9B 9C 9F,10B 12A 7 9B 9C,
10B 12A 12E 7 9B 9C
P08,11A 11B 12B 8 9A,10C 11A 11B 12B 8 9A,10C 11A 11B 12B 9A,
10C 11A 11B 12B 8,10C 11A 12B 8 9A
P11,11B 12C 9C 9F,11B 12C 8 9B 9C,11B 12C 9B 9C 9D,10D 10E 9B 9D,10D 10E 9C 9F 8
P12,10D 11B 12D 9D,10B 10D 11D 12D,10B 11C 12A 12D 9D,11C 12A 12D 9A 9D,
11B 12D 9A 9D 11D
P05,10C 12A 12B 9B,10C 12A 6 9A,10C 10E 10F 6 9A,10E 10F 11B 9D,10F 11B 12B 9B 9D
P09,10B 11E 12F 5 9F,10B 11E 11E 12F 9F,11D 11E 12F 9F,11D 11E 8 9F,11E 12F 5 8
P14,10C 11B 11C 7 8,10C 11B 7 8,10A 10C 11B 12A 9D,10A 11A 11C 9A 9F,11B 11C 9A
P15,10E 10E 11A 12E 8,10E 12E 12F 12C,10E 12B 12F,10E 12B 12C 12F 6,10E 11A 6 8
P16,10E 12C 12D 9E 10F,10E 11E 12C 12D,11D 11E 12C 9D,10D 10F 11D 9D,10D 10E 12C 9E
P17,10A 11C 12F 9B,11B 11C 11F 9B 9C,11B 12A 9C,10B 10E 11B 9B 9C,10A 10B 11C 9B
P18,12E 8 9E,10C 12A 12E 8 9E,10C 12A 8 9E,10C 12A 8 9E 12E,12A 12E 8 9E
P13,11F 7 9B 9C,10A 11F 9B 9E,10F 11F 5 9E,10C 10F 5,10C 10F 7 9C 10A
P19,11D 11E 9A 9E,10A 11C 12F 8 12A,10A 7 8 9F,11F 7 9B 9C,11D 11F 12A
P20,10A 11B 11D 12D 9B,11B 11D 9B,11B 11D 12D 9B,10A 11B 11D 12D,10A 11D 12D 9B
P21,10B 11C 11E 12C 9D,10B 11E 12C 9D,10B 11E 12C 9D,11C 11E 9D,11C 12C 9D 11C
P22,12A 12E 12F,10D 11D 12E 9E,10D 11D 12E 9E,10D 11D 12E 12F,10D 11D 12E 12F
P23,10E 10F 12D 6,11A 11B 12B 5,10D 12E 5,10B 10C 12C 5,10B 10C 6 9D
P24,11E 5 9C 9D,12D 5 9D,11E 12D 6 9A,11E 12D 6 9F,11E 12D 9B 9F
P25,10D 11F 11F 12B 12F,10D 11F 12F,10D 11F 12B 12F,10D 11F 12B 12F,11F 12B 12F
P26,10C 12B 6 8,10C 12B 12C 6,12B 12C 9D,10D 12C 9A,10F 11A 12B 9A 9E
P27,10B 10C 11A 11F,10A 10E 10F 11F,10E 10F 11C 12B,10E 10F 11B,10F 11F 12C
P28,10D 11A 8 9D,10D 9A 9D,10A 10C 12D,12B 12D 5 8,12A 8 10B
P29,10D 10F 12B 9C,12B 12C 9C,10B 10E 12C 9B,10B 12C 9B 9E,12B 12C
P30,10B 10C 11C 10F,10B 10F 12B,11C 12B 9E,10C 11C 12B,10B 10C 11C 9E
F1,10A 10B 12A,10A 10B 9A,11A 12A 9A,11A 12A 9A,10A 10B 11A
P10,5 9E,11D 11F 9D,12E 6 8,12D 12F 7 9F,11E 12F 9F
P33,10D 11C 11F,10D 11C 12D,10D 12D,11F 12C 9C,11F 12C 9C
P02,11A 9A,11A 5 9A,10A 11A 9A,10A 11F 12B,11A 9A
P03,12A 12C,10B 11D 12A,10B 11D 12C,10B 12A,10D 12A 6
P34,6 9F,6 9C,6 9C 9F,6 9C 9F,6 9C 9F
P35,10F,10E 10F 11A,10E 10F 11A,10E 10F 11A,10E 11A
P36,10A 11A 12A 9A,11A 12A,11A 12A,10A 9A,10A 9A
P37,10F 9F,11E 9F,11E 11F,11F 9E,9E 10F
P38,10E 12F,11F 9F,11F 9E,10D 10F,7 9D
F2,10C 10E 9B,10F 9A,10A,9C,10B 10D
P40,10E 12C,10E 9B,11C 9F,12E 9F,12E
P41,11C 5,11C 5,5,11C 5,11C 5
P42,,,10B 10D 10F,11A 10A,10C 10E 11B
P43,,7 9A,7 9A,7 9A,7 9A
P44,10A,6,10A 6,10A 6,10A 6
P31,6,7 9E,5 9F,8 9D,
P45,9A 9C,10A,9B 9E,10B 9E,
P46,11D 11E,11D 11E,11C 11F 8,,
P47,,,11D,11B 11D 12F,11D 12F 9C
F4,12E 9E,12E,12E,12E,12E
F3,9E,9E,9E,9E,9E
P32,,10A,12E,9E,10A
P39,,11A,11A 7,,7
P50,5 7,7 9F,,,
P51,7 6,,,,7 6
P52,,10E 10F,10E 10F,,
P53,5,5,,5,5
P54,11D 11F 12D,12F,,,
P55,,7 8,8,,
P56,,,5 7 6,,
P57,,,,,5 7 8
F5,,,11E,11E,
P58,,,,7 6,
P59,,,,12F,11F
P60,,,,,12A 12C
F6,11E,,,,
P61,,6,,,
Următorul program (provenit din [2]-IV, unde l-am conturat „pas cu pas” – încât acum ne scutim de „explicaţii”) transformă disRecast.csv într-un obiect tibble (salvat în disPeZile.RDS) cu structura prof|cls|zl, $prof şi $zl fiind de tip "factor" (profesorii fiind ordonaţi descrescător după numărul de ore pe săptămână):
# csv2df.R ## v. [2]-IV ("renormal.R") library(tidyverse) Dcsv <- read_csv("disRecast.csv") # distribuţia pe zile iniţială, format CSV splt <- function(Txt) unlist(strsplit(Txt, " ")) renormalize <- function(D) { D %>% gather("zl", "cls", 2:6, na.rm=TRUE) %>% mutate(ncl = unlist(lapply(.$cls, function(q) length(splt(q))))) %>% uncount(.$ncl) %>% split(., .$cls) %>% map_df(., function(G) { q <- splt(G$cls[1]) G$cls <- rep(q, nrow(G) %/% length(q)) as.data.frame(G) }) } Din <- renormalize(Dcsv) %>% select(-4) # elimină coloana $ncl Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") srt <- sort(table(Din$prof), decreasing=TRUE) Dzl <- as_tibble(Din) %>% mutate(prof = factor(prof, levels=names(srt), ordered=TRUE), zl = factor(zl, levels=Zile, ordered=TRUE)) %>% relocate(cls, .after=prof) %>% arrange(prof) saveRDS(Dzl, "disPeZile.RDS") # tibble, 839 x 3, $prof (ord.) | $cls | $zl (ord.)
Urmează să alocăm pe orele 1..7 ale zilei de lucru, orele profesorilor repartizate prin disPeZile.RDS într-o aceeaşi zi.
Noua filozofie a distribuţiei orare a lecţiilor unei zile
Preferăm să schimbăm notaţia claselor 5..8, pentru a nu confunda cumva cu orele zilei; le renotăm adăugând sufixul "G" (vine de la „Gimnaziu”):
Dis <- readRDS("disPeZile.RDS") for(k in 5:8) Dis[Dis$cls == as.character(k), ]$cls <- paste0(as.character(k),"G") saveRDS(Dis, file="disPeZile.RDS")
Reamintim ideea introdusă în [1] pentru repartizarea pe orele 1..7 ale zilei, a orelor profesorilor dintr-o aceeaşi zi, corectând totodată o anumită hibă.
„Orele profesorilor” sunt cupluri (profesor, clasă) şi vom mai zice lecţii, pentru a evita confuzia cu „orele 1..7 ale zilei”.
Mai întâi, separăm pe clase lecţiile repartizate în ziua respectivă; fiecărei clase îi corespund câte λ = 4..7 linii de lecţii, λ fiind numărul de ore din acea zi ale clasei. Tratăm pe rând clasele, într-o anumită ordine, eventual aleatorie.
Etichetăm liniile clasei curente cu una dintre permutările mulţimii {1, 2, ..., λ} (vom prelua din [1]-(I) fişierul "lstPerm47.RDS", care conţine lista celor 4 matrice de λ-permutări necesare); dacă ora alocată astfel unuia dintre profesorii de pe liniile respective coincide cu ora alocată lui la o clasă tratată anterior, atunci reetichetăm liniile clasei cu o altă λ-permutare (şi verificăm din nou, dacă există suprapuneri).
Avansând astfel, clasă după clasă – se poate întâmpla totuşi (undeva spre final) ca reetichetarea clasei curente să eşueze: pentru toate λ-permutările posibile încercate, există suprapuneri cu ore alocate anterior, profesorilor clasei respective. Această hibă nu s-a manifestat pentru încadrările din [1] şi [2], dar pentru încadrarea de faţă – care este mai densă – orarul final obţinut aplicând direct programul anterior, omite câte o clasă în unele zile (deci liniile acelei clase n-au putut fi etichetate fără suprapuneri).
Corectăm acum, această hibă (dar într-o manieră „nedeterministă”, cam cum am procedat şi la repartizarea pe zile a orelor): dacă pentru clasa curentă se epuizează toate λ-permutările (negăsind niciuna care să evite suprapuneri cu alocări făcute anterior), atunci abandonăm complet tratarea în curs a claselor, ordonăm aleatoriu grupurile de linii aferente claselor şi o luăm de la capăt, tratând clasele în noua ordine a acestora – repetând „abandonarea” şi „reluarea” până ce se reuşeşte tratarea tuturor claselor (practic, factorialul numărului de clase este foarte mare, încât cam trebuie să nimerim la un moment dat, o ordine a claselor care să permită „tratarea” tuturora).
Existenţa cuplajelor creşte binişor complexitatea acestei tratări, trebuind făcute verificări de suprapunere suplimentare (iar riscul epuizării λ-permutărilor creşte); în plus, formularea corectă a acestor verificări este complicată. Să zicem de exemplu, că la clasa curentă apare "F1"; va trebui verificat nu numai că ora alocată lui nu se suprapune cu una alocată lui anterior, dar şi că nu se suprapune cu o oră alocată anterior profesorilor cuplaţi de "F1" – iar pentru fiecare dintre aceştia va trebui verificat, oricând ar apărea între profesorii unei clase, că ora alocată nu se suprapune cu o oră alocată deja lui "F1" (şi la fel, pentru ceilalţi profesori fictivi).
Deocamdată preferăm să nu complicăm programul şi generăm orarul zilei ca şi când toţi profesorii ar fi independenţi între ei; în fond, pe o zi avem numai câteva cuplaje şi va fi uşor să rezolvăm interactiv eventualele suprapuneri apărute pe orarul generat pentru ziua respectivă.
Să ne amintim că undeva mai sus am constituit fişierul "together.txt", înregistrând cuplajele existente în încadrarea profesorilor; după ce am generat distribuţia pe zile a orelor din încadrare, ne-am ghidat după acest fişier pentru a muta interactiv anumite clase dintr-o zi în alta, astfel încât să eliminăm situaţiile în care vreunul dintre profesorii cuplaţi pe acele clase ar avea mai mult de 6 ore pe zi.
Dar ne-a scăpat din vedere, să şi actualizăm fişierul respectiv, în urma mutărilor de clase pe care le-am făcut; să reconstituim acum, cuplajele existente pe fiecare zi, folosind nu forma normalizată disPeZile.RDS a distribuţiei pe zile, ci mult mai simplu – folosind direct fişierul CSV din care a provenit aceasta:
# cuplaje.R # alocarea pe zile a orelor cuplate prin profesorii "fictivi" library(tidyverse) Dcsv <- read_csv("disRecast.csv") # din care produsesem "disPeZile.RDS" Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") prFi <- list(F1 = c("P02", "P03"), F2 = c("P31", "P10"), F3 = c("P32", "P39"), F4 = c("P32", "P05"), F5 = c("P09", "P13"), F6 = c("P09", "P15")) tags <- paste0("F", 1:6) # cheile din lista 'prFi' for(day in Zile) for(key in tags) { D <- Dcsv %>% filter(prof %in% c(key, prFi[[key]])) %>% select(prof, day) # vizează numai profesorii fictivi din acea zi if(!is.na(D[D$prof == key, 2])) { D %>% rbind(., c(paste("---", day, "---"), "")) %>% write_csv(., file = "together.csv", append = TRUE) } }
După ce obţinem orarul pentru ziua de "Lu" de exemplu, vom urmări conţinutul fişierului together.csv pentru a opera prin SWAP (în aplicaţia /dayRecast) mutările cuvenite de ore, cam cum ilustrăm aici:
F1,10A 10B 12A # de plasat în „ferestre comune” ale profesorilor "P02" şi "P03" P02,11A 9A P03,12A 12C --- Lu ---, P10,5 9E F2,10C 10E 9B # de plasat în „ferestre comune” ale profesorilor "P10" şi "P31" P31,6 # De exemplu: P10 - orele 1 şi 2; P31 - ora 2; P10+P31 - orele 3, 4, 5 --- Lu ---, F3,9E # aparent, se poate plasa oricând, fiindcă "P32" şi "P39" sunt liberi P32,NA # nu are ore proprii, în ziua respectivă P39,NA --- Lu ---, P05,10C 12A 12B 9B F4,12E 9E P32,NA # Atenţie: are deja o oră! (cu "P39", mai sus) --- Lu ---, P09,10B 11E 12F 5 9F P15,10E 10E 11A 12E 8 F6,11E # de plasat în unica fereastră comună a profesorilor "P15" şi "P09" --- Lu ---,
Să recunoaştem totuşi că vom avea şi cazuri mai complicate – de exemplu, "P32" este cuplat şi prin "F3" şi prin "F4" – dar oricum, ni se pare clar că va fi mai uşor de pus la punct situaţiile de cuplaj operând interactiv cum am sugerat mai sus, decât imaginând vreo secvenţă de program care să aibă în vedere toate situaţiile.
Programul de distribuţie orară a lecţiilor unei zile
Nu ne mai gândim ca în [1], să obţineam „deodată” toate cele 5 orare zilnice; este preferabil să lucrăm pe fiecare zi în parte, repetând programul pentru ziua respectivă dacă orarul tocmai furnizat pentru ea nu este suficient de convenabil.
În directorul de lucru curent s-au adunat deja multe fişiere (".R", ".RDS", ".csv"); dar mai departe, avem (neapărat) nevoie numai de lista matricelor de λ-permutări (din fişierul lstPerm47.RDS) şi de cele 5 distribuţii ale orelor corespunzătoare fiecărei zile (extrase din "disPeZile.RDS"). Se cuvine să înfiinţăm un subdirector /byDays/, care să conţină aceste fişiere şi în care să generăm apoi, cele 5 orare zilnice.
Prin următorul program (lansat din directorul părinte al lui /byDays/) extragem din distribuţia pe zile a tuturor orelor încadrării, distribuţiile corespunzătoare fiecărei zile în parte, obţinând fişierele byDays/dis_{zi}.RDS (unde "{zi}" este "Lu", "Ma", etc.); în plus, constituim în Bits.RDS un „vector cu nume”, care ne va servi pentru a controla în privinţa suprapunerilor (v. [1]), alocarea pe orele zilei a lecţiilor clasei curent tratate:
library(tidyverse) Dzl <- readRDS("disPeZile.RDS") # distribuţia pe zile a orelor, prof|cls|zl Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") # orele repartizate zilei, ordonate după profesori şi separate după clasă disOfDay <- function(zi) { Dzl %>% filter(zl == zi) %>% select(prof, cls) %>% arrange(prof) %>% # arrange(desc(prof)) split(.$cls) %>% saveRDS(., file = paste0("byDays/dis_", zi, ".RDS")) } lapply(Zile, disOfDay) Bits <- rep(0L, nlevels(Dzl$prof)) # urma alocărilor de ore (v. [1]), iniţial 0 names(Bits) <- levels(Dzl$prof) saveRDS(Bits, file="Bits.RDS")
Deocamdată avem:
vb@Home:~/21mar/ORARE$ ls byDays Bits.RDS dis_Jo.RDS dis_Lu.RDS dis_Ma.RDS dis_Mi.RDS dis_Vi.RDS lstPerm47.RDS
Vom obţine orarul uneia sau alteia dintre zile, după această schemă:
lu <- readRDS("dis_Lu.RDS") # lecţiile prof|cls repartizate în ziua 'Lu' hLu <- mountHtoDay(lu) # prof|cls|ora (alocă fiecare lecţie pe orele 1..7)
mountHtoDay() fiind funcţia pe care am introdus-o în [1] şi pe care o reluăm acum, corectând hiba pe care am evidenţiat-o undeva mai sus; am preferat să introducem lista de λ-permutări precum şi tabloul octeţilor de alocare Bits în afara contextului funcţiei (era posibil şi în interior, dar atunci readRDS() ar fi fost invocată de mai multe ori şi în plus, dacă vrem să folosim ulterior şi valorile rămase în Bits atunci ele ar trebui salvate, cu saveRDS(), înainte de a încheia execuţia – altfel se pierd):
# set_hours_day.R (setează orele 1..7 lecţiilor repartizate într-o aceeaşi zi) library(tidyverse) Pore <- readRDS("lstPerm47.RDS") # lista matricelor de permutări (de 4..7 ore) Bits <- readRDS("Bits.RDS") # alocările orelor prof., pe câte un octet (iniţial 0) ## alocă profesorii pe orele zilei, pentru fiecare clasă mountHtoDay <- function(Z) { # 'tibble' <ord>prof|cls, split()-at pe clase # iniţializează octeţii de alocare, copiind tabloul global 'Bits' bith <- Bits # <- readRDS("Bits.RDS") # alocă pe orele 1..7, orele (lecţiile) unei clase mountHtoCls <- function(Q) { # 'Q' conţine liniile din Z cu o aceeaşi 'cls' if(succ == FALSE) return(NULL) # cat(Q$cls[1], " ") ## dacă vrem să vedem clasele tratate pe parcurs mpr <- Pore[[nrow(Q)-3]] # matricea de permutări corespunzătoare clasei for(i in 1:ncol(mpr)) { po <- mpr[, i] S <- Q %>% mutate(ora = po) # etichetează cu permutarea curentă # vectorul octeţilor de ore asociaţi acestei permutări: bis <- bitwShiftL(1, S$ora - 1) # vectorul octeţilor de ore alocate deja profesorilor clasei: bhp <- bith[S$prof] # Dacă există suprapuneri (de ore) între cei doi vectori, # atunci angajează coloana următoare a matricei de permutări, # dacă mai există una (altfel, abandonează) if(i == ncol(mpr) & any(bitwAnd(bhp, bis) > 0)) { succ <<- FALSE break } if(any(bitwAnd(bhp, bis) > 0)) next # se presupune că la o aceeaşi clasă, avem cel mult 2 ore de profesor j <- anyDuplicated(names(bhp)) if(j > 0) { # dacă în Z, profesorul are 2 ore la acea clasă bis[j-1] <- bis[j] <- bis[j-1] + bis[j] } # actualizează global, octeţii de alocare: bith[S$prof] <<- bitwOr(bhp, bis) return(S) } } succ <- TRUE # aplică montHtoDay() pentru fiecare clasă, în ordinea iniţială a claselor orar <- Z %>% map_df(., function(K) mountHtoCls(K)) while(succ == FALSE) { # print("insucc") ## nu se poate trece de clasa curentă succ <- TRUE bith <- Bits # <- readRDS("Bits.RDS"); reiniţializează octeţii de alocare orar <- Z %>% sample(.) %>% # ordonează aleatoriu lista tabelelor claselor map_df(., function(K) mountHtoCls(K)) # reia alocarea orelor } Bits <<- bith # salvează octeţii de alocare rezultaţi în final return(orar) # orarul zilei, prof|cls|ora }
Iată o mostră de tratare, activând afişarea pe parcurs a unor informaţii:
> rm(list=ls()) # elimină din memorie obiectele create în sesiunea curentă > source("set_hours_day.R") > lu <- readRDS("dis_Lu.RDS") # lecţiile prof|cls din ziua 'Lu' > orLu <- mountHtoDay(lu) # orarul zilei 'Lu' 10A 10B 10C 10D 10E 10F 11A 11B 11C 11D 11E 11F 12A 12B 12C 12D 12E 12F 5G 6G 7G 8G 9A 9B 9C 9D [1] "insucc" 12A 9F 11A 9E 12C 10C 12E 12F 10B 11F 9B 5G 9C 7G 10A 12B 11E 10E 11D 10F 9A 10D 9D 8G 11B [1] "insucc" #... ... ... 7G 12B 11F 10B 8G 12C 11B 12A 11D 12E 12F 9F 9B 10C 9D 11A 12D 11C 5G 10D 9E 11E 10E 9C 6G 9A 10A 10F >
Mai întâi, clasele au fost tratate în ordinea iniţială (alfabetică) – dar nu s-a putut trece de clasa 9D (epuizând toate cele 720 de permutări posibile pentru cele 6 ore din acea zi ale clasei 9D). Apoi, seturile de linii corespunzătoare claselor au fost reordonate (aleatoriu), dar nici în noua ordine a claselor (12A, 9F, 11A, etc.) nu s-a reuşit tratarea tuturora (clasa 11B are 5 ore în acea zi şi pentru oricare 5-permutare încercată, există suprapuneri cu ore alocate unor clase tratate anterior).
După un număr de asemenea insuccese (poate în vreo două minute, poate mai mult), se nimereşte totuşi una dintre ordonările de clase (mai sus, 7G, 12B, 11F, etc.) care asigură tratarea tuturora, obţinând un orar pentru ziua respectivă; repetând programul, într-o altă sesiune de lucru, va rezulta câte un alt orar al zilei respective, diferit de cel anterior obţinut (în măsura în care este adevărat că există numeroase reordonări ale claselor care să asigure tratarea tuturora).
Putem vedea orarul unei clase (şi analog, al unui profesor) de exemplu astfel:
> orr <- orLu %>% arrange(ora) %>% split(.$cls) # sau, %>% split(.$prof) > orr$`9A` # respectiv, orr$`P02` # A tibble: 6 x 3 prof cls ora <ord> <chr> <int> P19 9A 1 P02 9A 2 P36 9A 3 P45 9A 4 P08 9A 5 P01 9A 6
Eventual, pentru prelucrări ulterioare, vom păstra orarul obţinut, într-un fişier:
> saveRDS(orLu, file="orar_Lu.RDS")
În final, putem investiga şi tabelul Bits:
> Bits # octeţii cu alocarea pe ore 1..7 a profesorilor P01 P04 P06 P07 P08 P11 P12 P05 P09 P14 P15 P16 P17 P18 P13 P19 P20 P21 P22 P23 63 63 63 15 47 15 23 15 31 31 31 31 15 14 27 15 47 61 26 39 # etc.
şi nu doar pentru a număra ferestrele profesorilor (v. [1]), dar şi pentru a vedea în ce măsură sunt posibile cuplajele prin profesorii fictivi (care nu au fost avute în vedere de program – rămânând de rezolvat interactiv); de exemplu, avem:
> Bits[c("F1", "P02", "P03")] F1 P02 P03 70 18 40 # 70=1000110 18=0010010 40=0101000 biţii pentru ora7, ora6, ..., ora1
şi urmărind biţii octeţilor respectivi, constatăm o singură nepotrivire: "P02" şi "P03" nu pot intra împreună în ora a 2-a indicată de "F1" (prin bitul de rang 1, de valoare 1), fiindcă "P02" este ocupat deja în acea oră. Desigur, o singură nepotrivire va fi uşor de corectat interactiv…
Cuplajul este posibil dacă bitwAnd(Bits["F1"], Bits["P02"]) şi bitwAnd(Bits["F1"], Bits["P03"]) au valoarea zero; cu toate că este relativ simplă, o asemenea condiţionare este delicat de integrat în programul de mai sus – trebuind aplicată numai claselor la care apare măcar unul dintre cei trei profesori (şi am constatat că e greu totuşi, de formulat un test eficient „apare profesorul la clasa curentă?”, mai având în vedere şi toate cuplajele, prin toţi profesorii fictivi consideraţi).
Finalizarea interactivă a orarului zilei
Orarul orar_Lu.RDS obţinut mai sus (sau orarul vreunei alte zile, obţinut analog) conţine multe ferestre şi (cum am evidenţiat deja) unele suprapuneri de ore la profesori cuplaţi prin cei fictivi; aplicaţia /dayRecast (HTML + jQuery) permite corectarea interactivă a acestor neajunsuri, tabelând profesorii şi clasele alocate pe orele 1..7 ale zilei şi prevăzând operaţia SWAP, prin care se pot schimba alocările iniţiale.
Dar avem de transformat „formatul” prof|cls|ora specific pentru orar_Lu.RDS, într-un fişier CSV cu structura "prof, ora1, ora2, ..., ora7" (care să fie apoi „pastat” în elementul <textarea> al aplicaţiei). Dar… vrem ceva mai mult: să reordonăm liniile încât cele corespunzătoare profesorilor cuplaţi să fie grupate la începutul tabelului (pentru a ne uşura intervenţia interactivă prin operaţiile SWAP):
# rds2csv.R library(tidyverse) file <- "orar_" # Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") format_csv <- function(zi) { readRDS(paste0(file, zi, ".RDS")) %>% arrange(prof) %>% split(.$prof) %>% map_df(., function(Q) spread(Q, ora, cls)) } # orz <- format_csv("Lu") # lista tuturor cuplajelor prin profesorii fictivi prFi <- list(F1 = c("P02", "P03"), F2 = c("P31", "P10"), F3 = c("P32", "P39"), F4 = c("P32", "P05"), F5 = c("P09", "P13"), F6 = c("P09", "P15")) rds2csv <- function(zi) { orz <- format_csv(zi) # vectorul profesorilor cuplaţi în această 'zi' cplv <- unlist(lapply(paste0("F", 1:6), function(k) {if(any(orz$prof == k)) c(k, prFi[[k]]) })) # vectorul tuturor profesorilor din acea 'zi', începând cu cei cuplaţi ord_pr <- c(cplv, setdiff(orz$prof, cplv)) # ?? cplv <- unique(cplv) [*] # indecşii liniilor din 'orz', în ordinea dată de 'ord_pr' row_ids <- unlist(lapply(ord_pr, function(pr, D) { which(D$prof == pr) }, D = orz)) orz <- orz[row_ids, ] # pe primele linii avem acum cuplurile din acea zi write_csv(orz, file=paste0(file, zi, ".csv"), na = "-", col_names=TRUE) }
De exemplu, prin rds2csv("Lu") obţinem "orar_Lu.csv", având pe primele linii:

prof,1,2,3,4,5,6,7 F1,-,10A,12A,-,-,-,10B P02,-,9A,-,-,11A,-,- P03,-,-,-,12C,-,12A,- F2,-,10E,-,10C,-,9B,- P31,-,-,-,-,6G,-,- P10,-,9E,5G,-,-,-,- F3,-,-,-,-,-,9E,- F4,-,-,-,-,9E,12E,- P05,9B,10C,12B,-,12A,-,- F6,-,-,-,-,-,11E,- P09,11E,5G,10B,9F,12F,-,- P15,8G,11A,12E,10E,10E,-,- P01,10B,6G,10A,11D,12B,9A,- P04,10D,12E,12D,12F,9D,9F,- ... ... ...
Reordonând astfel liniile, vedem uşor de exemplu, că "P02" şi "P03" nu pot intra împreună la clasa 10A (pe care sunt cuplaţi prin F1); sau, că în acest moment "P09" şi "P15" îşi pot face şi orele proprii şi ora la 11E (pe care sunt cuplaţi prin F6).
Mai observăm că F5 nu apare în ziua respectivă; linia lui F3 nu este succedată de cele două linii care ar corespunde profesorilor pe care îi cuplează, ceea ce înseamnă că aceştia nu au ore proprii în această zi – deci 9E se poate muta dacă este cazul (pentru a reduce ferestre la alţi profesori) în oricare oră 1..7 de pe linia lui F3.
Procedând cam cum am arătat în [1] (III), am reuşit după un anumit număr de operaţii SWAP să corelez între ei profesorii cuplaţi şi să reduc cele 42 de ferestre existente iniţial (cum arată "Gaps" în imaginea redată mai sus) la numai 8, toate de câte o singură oră (nu-i cazul să ne lăudăm: pe orarul original de pe care am extras încadrarea, pentru orele de "Lu" – altele însă, decât cele care ne-au rezultat aici – existau numai 7 ferestre):
> rc8 <- read_csv("Recast8.csv") # din aplicaţia /dayRecast/, prin "Export" > print(rc8, n=Inf) prof `1` `2` `3` `4` `5` `6` `7` 1 F1 10A 12A 10B - - - - # P02 + P03 2 P02 - - - 9A 11A - - 3 P03 - - - 12C 12A - - 4 F2 - - - 10C 9B 10E - # P31 + P10 5 P31 - - 6G - - - - 6 P10 - 5G 9E - - - - 7 F3 - - - 9E - - - # P32 + P39 (P32 este dublu cuplat) 8 F4 - - - - 9E 12E - # P32 + P05 9 P05 12B 10C 9B 12A - - - 10 F6 - - - - - 11E - # P09 + P15 11 P09 10B 11E 9F 5G 12F - - 12 P15 11A 8G 10E 10E 12E - - # 10E: P15 + P48 (fără fereastră) 13 P01 11D 6G 10A - 12B 9A 10B 14 P04 9F 12E 9D 12F 12D 10D - 15 P06 11B 9D 9C 9B 9F 7G - 16 P07 - - 7G 12E 10B 12A - 17 P08 9A 12B 11A 11B 8G - - 18 P11 9C 12C 11B 9F - - - 19 P12 - - 10D 12D 9D 11B - 20 P14 7G 11B - 11C 10C 8G - 21 P16 10F 12D 12C - 10E 9E - 22 P17 11C 9B 12F 10A - - - 23 P18 8G 9E 12E - - - - 24 P13 9B 9C 11F 7G - - - 25 P19 9E 9A 11E 11D - - - 26 P20 12D 10A 11D - 11B 9B - 27 P21 9D 11C - 11E 12C 10B - 28 P22 12E 12F 12A - - - - 29 P23 10E 10F 12D 6G - - - 30 P24 - - 5G 9C 11E 9D - 31 P25 12F 11F - 12B 10D 11F - 32 P26 - - 12B 8G 6G 10C - 33 P27 - - 10C 10B 11F 11A - 34 P28 10D 11A 8G 9D - - - 35 P29 - - 10F 10D 9C 12B - 36 P30 10C 10B - 10F 11C - - 37 P33 11F 10D 11C - - - - 38 P34 6G 9F - - - - - 39 P35 - - - - - 10F - 40 P36 12A - 9A 11A 10A - - 41 P37 - - - - 10F 9F - 42 P38 - - - - - 12F 10E 43 P40 12C 10E - - - - - 44 P41 - - - - 5G 11C - 45 P44 - - - - - 10A - 46 P45 - - - - 9A 9C - 47 P46 11E 11D - - - - - 48 P50 5G 7G - - - - - 49 P51 - - - - 7G 6G - 50 P53 - - - - - 5G - 51 P54 - - - 11F 11D 12D -
Dar… asta ne interesează aici, „să finalizăm orarul” pe o zi sau alta?
Finalizarea programelor…
Adăugăm în programul "set_hours_day.R" o funcţie utilitară ("helper") care să ne furnizeze (apelând mountHtoDay()) fişierul "orar_{zi}.RDS" pentru ziua indicată:
# în set_hours_day.R orarofday <- function(zi) { tb <- readRDS(paste0("dis_", zi, ".RDS")) orZ <- mountHtoDay(tb) saveRDS(orZ, file=paste0("orar_", zi, ".RDS")) }
Se întâmplă că "orar_Ma.RDS" este produs aproape imediat (cu tratarea claselor în ordinea lor iniţială, fără să mai apară "insucc"):
> source("set_hours_day.R") > orMa <- orarofday("Ma") 10A 10B 10C 10D 10E 10F 11A 11B 11C 11D 11E 11F 12A 12B 12C 12D 12E 12F 5G 6G 7G 8G 9A 9B 9C 9D 9E 9F >
Prin rds2csv("Ma") am obţinut "orar_Ma.csv", pe care l-am pasat aplicaţiei /dayRecast – dar acţionând "Load", în loc de tabelul HTML cuvenit, am obţinut un mesaj de atenţionare: "Suprapuneri: P32 / P32: 10A, ora 7"…
Aceasta înseamnă că P32 apare de două ori, în tabelul HTML – ceea ce nu trebuia să se întâmple; şi într-adevăr, în "orar_Ma.csv" găsim:
F3,-,-,-,-,-,9E,- # cuplează P32 şi P39 P32,-,-,-,-,-,-,10A P39,-,-,-,-,11A,-,- F4,-,-,12E,-,-,-,- # cuplează P32 şi P05 P32,-,-,-,-,-,-,10A # ?? se produce a doua oară, linia lui P32 P05,6G,12A,10C,9A,-,-,-
Fiindcă "P32" este cuplat şi prin F3 şi prin F4, linia sa a fost inclusă de două ori.
Prin urmare, avem de corectat funcţia rds2csv() (în locul marcat cu [*]), aplicând unique() vectorului profesorilor cuplaţi:
## corectură, în funcţia rds2csv() ## # vectorul profesorilor din acea 'zi', începând cu cei cuplaţi cplv <- unique(cplv) # evită dublarea liniei, când profesorul este dublu cuplat ord_pr <- c(cplv, setdiff(orz$prof, cplv))
Vedem deci, încă o dată, că „munca interactivă” este totuşi importantă pentru punerea la punct a programelor…
După corectura menţionată, operând în /dayRecast obţinem eventual această rezolvare a situaţiilor de cuplaj:
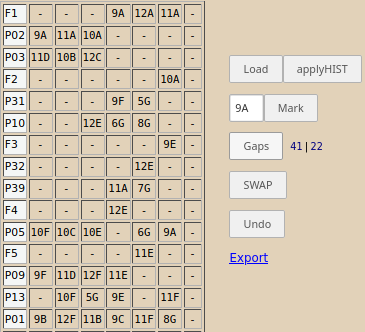
P02 şi P03 fac individual primele 3 ore şi apoi intră împreună următoarele 3 ore, la clasele indicate de F1. O situaţie analogă avem pentru P31 şi P10.
Interesant (şi complicat de tratat) este cazul lui P32, care cuplează şi cu F3 şi cu F4: întâi, P32 intră împreună cu P05 la clasa 12E (pe care este cuplat prin F4), apoi continuă singur cu clasa 12E, apoi intră împreună cu P39 (cu care este cuplat prin F3) la clasa 9E.
De observat că P05 şi P13 au câte o fereastră aparentă – în care P05 intră împreună cu P32 la clasa 12E, iar P13 intră împreună cu P09 la clasa 11E (pe care sunt cuplaţi prin F5); altfel, în situaţia redată pe imaginea de mai sus – pe cele 14 linii corespunzătoare profesorilor cuplaţi nu avem nicio fereastră reală.
Deci numărul curent de ferestre, afişat la "Gaps", ar trebui cumva corectat (este 20, nu 22); dar bineînţeles că nu vom complica aplicaţia, pentru atâta lucru (vrem doar să evidenţiem că mereu vom găsi câte ceva de „finalizat”).
Am reuşit până la urmă să reducem numărul de ferestre (reale) la 6 – dar trebuie să recunoaştem că n-a fost deloc uşor, trebuind să verificăm mereu dacă prin SWAP-ul curent nu deteriorăm cuplajele (fără nicio fereastră) arătate mai sus (apropo: iarăşi nu-i cazul să ne lăudăm – pe orarul original în ziua "Ma" există numai 5 ferestre reale; dar subliniem că pe orarul original orele sunt altfel distribuite pe zile, faţă de cazul nostru).
Pentru a uşura această muncă ar fi de adăugat în aplicaţia /dayRecast o funcţie care să verifice dacă prin operaţia SWAP curentă se produce vreo modificare de structură pe primele linii ale tabelului HTML (cele corespunzătoare cuplajelor, în cazul de aici – primele 14 linii); desigur, apare un aspect delicat: funcţia respectivă trebuie „activată” după ce vom fi stabilit structura de bază a cuplajelor.
Am evidenţiat mai sus câteva aspecte de corectat sau de completat, mai mult sau mai puţin importante; dar adevărata „finalizare” este încă departe şi ar consta în strângerea programelor respective într-un pachet R unitar (plus aplicaţii interactive, HTML+jQuery), care să exteriorizeze un set de funcţii cu denumiri bine alese, acoperind etapele principale de lucru; pe lângă etapele vizate până acum (preluarea şi normalizarea încadrării; distribuirea orelor pe zilele de lucru; obţinerea orarului unei zile), mai trebuie abordată şi chestiunea prezentării finale a orarului – de exemplu, ca site HTML (care să poată fi uşor de actualizat, în cazul schimbării orarului).
vezi Cărţile mele (de programare)