Distribuţia orară a distribuţiei pe zile a orelor şcolii (III)
Reveniri…
Programul mount_in_days.R prelua din tb1202x3.RDS, distribuţia pe zile a orelor şcolii şi adăuga coloana $ora pe liniile corespunzătoare unei aceleiaşi zile, alocând profesorii pe orele zilei, pentru fiecare clasă:
for(zi in Zile) { lTMT[[zi]] <- Dzl %>% filter(zl == zi) %>% select(prof, cls) %>% arrange(prof) %>% # arrange(desc(prof)) %>% split(.$cls) %>% mountHtoDay(.) }
Înainte de a aplica mountHtoDay() fiecărei clase, liniile corespunzătoare zilei respective au fost ordonate (prin arrange()) după $prof – adică descrescător după numărul de ore pe săptămână ale profesorilor (amintim că $prof este "factor ordonat", în care ordinea nivelelor reflectă descrescător numărul total de ore). Orarul rezultat (în tmt5.RDS) avea în total, 320 de ferestre (v.[1]).
Dacă repetăm programul mount_in_days.R, schimbând însă linia "arrange(prof) %>%" cu "arrange(desc(prof)) %>%" (ordonând liniile crescător după numărul total de ore) – obţinem un nou orar (în tmt6.RDS), cu un total de numai 233 de ferestre; iar timpul de execuţie în acest caz a fost aproape 1 minut (în primul caz, era aproape 5 minute).
Cei care au puţine ore, pot avea multe ferestre; de exemplu, 2 ore pot fi alocate primeia şi ultimeia din zi – rezultând 5 ferestre. Începând alocarea orelor cu cei care au puţine ore, se profită şi de faptul că aceştia au puţine clase comune – încât ei vor fi alocaţi cel mai adesea pe primele ore, aproape fără ferestre; profesorii cu măcar 5 ore în ziua respectivă pot avea maximum 2 ferestre şi lăsându-i la sfârşit, avem şansa ca numărul total de ferestre să crească mai puţin, decât în cazul când am începe alocarea orelor în sens invers.
În funcţie de proporţia celor cu multe ore, faţă de cei cu puţine ore pe săptămână – obţinem un orar cu multe sau cu mai puţine ferestre, după cum începem alocarea pe orele zilei cu unii (cei cu multe ore), respectiv cu ceilalţi.
Dar şi dacă sunt 320 şi dacă sunt 233 de ferestre – practic, timpul pentru reducerea interactivă a ferestrelor rezultate pe o zi este cam acelaşi (o oră, pentru a reduce de la 60-70 ferestre la numai 10-15 – deci pentru întregul orar, cam 4-5 ore de lucru).
Practica reducerii ferestrelor
Cu aplicaţia /dayRecast putem reduce (într-o anumită măsură) ferestrele din orarele zilnice rezultate; evidenţiem aici câteva principii de lucru.
Orarul zilei poate fi pastat direct în caseta <textarea” – dar cel mai bine este să-l înscriem în fişierul HTML, în locul orarului existent (preluând mai întâi fişierele aplicaţiei, eventual de la github). Pe orar, coloanele corespunzătoare orelor zilei trebuie să conţină fiecare clasă câte o singură dată; desigur, o clasă care în ziua respectivă are numai 4 ore (respectiv 5, sau 6 ore) figurează numai în primele 4 coloane (respectiv, în primele 5 sau 6 coloane).
După ce marcăm prin click o clasă K şi pe aceeaşi linie, un loc liber '-' – click pe SWAP va muta K pe locul liber respectiv; dar această „mutare” înseamnă de fapt o serie întreagă de mutări de clase între cele două coloane, trebuind respectată regula unicităţii clasei pe coloană (clasa K exista deja pe coloana „destinaţie” a operaţiei SWAP, deci trebuie mutată pe coloana „sursă”, de unde tocmai a dispărut – dar la această nouă „destinaţie” există o anumită clasă, care trebuie iarăşi mutată, ş.a.m.d. – până ce în sfârşit, „clasa” de mutat ajunge să fie '-').
În orice caz, SWAP angajează numai două coloane şi este posibilă această „strategie”: operăm de sus în jos mai întâi pe primele două coloane, apoi pe a doua şi a treia, apoi pe a treia şi a patra coloană, ş.a.m.d. – urmărind de fiecare dată să aliniem clasele de pe fiecare linie fie spre stânga, fie spre dreapta – astfel încât '-' să apară eventual înainte sau/şi după clase, dar nu între clase. Procedeul merge (şi repede) cam până la momentul când putem constata că profesorii din prima jumătate a orarului (presupunem că este cea mai aglomerată, adică am început cu profesorii care au multe ore) nu mai au ferestre; pentru cealaltă jumătate a orarului lucrurile se complică, trebuind folosit SWAP (şi Undo) între diverse coloane, urmărind de fiecare dată ce se întâmplă cu numărul curent de ferestre şi având grijă să nu stricăm prea mult, aranjamentele din prima jumătate.
O altă strategie de lucru posibilă (pe care am folosit-o cu precădere) constă în a evidenţia pe rând orarul fiecărei clase (folosind Mark) şi a folosi SWAP pentru a reduce pe cât se poate ferestrele existente la un anumit moment al lucrului, pe orarul clasei respective (ignorând într-o primă etapă, efectul lui SWAP pe celelalte linii ale orarului):
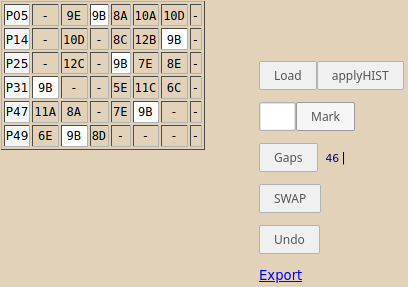
Orarul iniţial avea peste 60 de ferestre; cum-necum am reuşit să reduc numărul de ferestre la 46 şi trebuind să întrerup lucrul, am salvat prin Export starea curentă a orarului, împreună cu lista "History" a mutărilor efectuate prin SWAP (începând de la orarul iniţial); ulterior, am înlocuit în fişierul "dayRecast.html" conţinutul lui <textarea>, cu orarul din fişierul obţinut prin Export – încât reîncărcând în browser "dayRecast.html", avem imaginea de mai sus (după ce am folosit Mark pentru clasa 9B).
În ziua respectivă, profesorii clasei 9B au în total 5 ferestre (iar "P31" are două ferestre consecutive); nu-i chiar banal, de eliminat toate cele 5 ferestre – dar dacă reuşim şi dacă prin aceasta, numărul total de ferestre se reduce la exact 41 (= 46 - 5), sau se reduce la mai puţin de 41, atunci putem fi siguri că (deşi am operat numai la 9B) numărul de ferestre de la profesorii celorlalte clase nu are de suferit (fiind posibil totuşi ca o fereastră să dispară de la unul şi să apară în plus, la un altul).
Iată lista operaţiilor SWAP folosite, în termenii înregistraţi în lista "History" (indice_rând, indice_coloană_sursă, indice_coloană_destinaţie – cu precizarea că "indice" începe de la 0):
30 1 3 # la P31: 9B din coloana 1 se mută în coloana 3; mutare inversă la P05 30 3 2 # la P31: 9B din coloana 3 se mută în coloana 2; invers (9B cu 8D), la P49 4 1 3 # la P05: 9B col.1 => col.3 şi invers: la P49, 9B col.3 <-> 6E col.1 13 6 3 # la P14: 9B col.6 => col.3 şi la P05: 10D col.6 <-> 9B col.3 46 5 3 # la P47: 9B col.5 => col.3 şi la P14: 9B col.3 <-> 12B col.5 24 4 3 30 2 3 24 2 4
Aceste 8 operaţii SWAP elimină toate cele 5 ferestre, iar totalul ferestrelor se reduce la exact 41 (=46-5, deci profesorii de la celelalte clase nu sunt afectaţi):
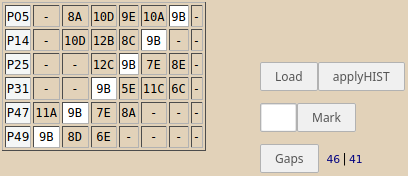
Mai departe (în principiu) procedăm şi cu celelalte clase, pe rând, cam la fel cum am evidenţiat mai sus pentru 9B – urmărind mereu ca numărul total de ferestre să scadă de fiecare dată, pe cât se poate, cel puţin cu numărul de ferestre ale profesorilor clasei curente; desigur, procedeul nu este liniar: se poate de exemplu, ca pe parcurs să dispară o fereastră de la un profesor şi să apară în plus, la unul dintre profesorii uneia dintre clasele operate la un pas anterior.
O a treia strategie de lucru avută în vedere constă în a opera cu SWAP (analog operării de mai sus la clasa 9B) pe lista profesorilor care au clase comune; în acest scop, am prevăzut un handler de click pe coloana "prof" (click pe numele "P08" de exemplu, vizualizează numai liniile profesorilor care au clase în comun cu "P08").
Evidenţierea ferestrelor
Operând cam cum am arătat mai sus, am reuşit să reduc numărul ferestrelor de la 60-70, la 10-14 (şi toate, de câte o singură oră) – obţinând fişierele "RecastLu.csv" etc. (redenumite după zile); aceste fişiere nu conţin şi secţiunea "History", adăugată prin Export (fiindcă ideea adăugării acestei secţiuni şi a operaţiei applyHIST a apărut „între timp”); am completat cele 5 fişiere .csv cu antetul "prof,1,2,3,4,5,6,7" – încât le putem „citi” direct în R ca obiecte "tibble":
# csv2df.R library(tidyverse) Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi") lCSV <- c(paste0("Recast", Zile, ".csv")) # fişierele "RecastLu.csv", etc. DFO <- map_df(1:5, function(i) { read_csv(lCSV[i]) %>% mutate(., zl = factor(Zile, levels = Zile, ordered=TRUE)[i]) }) > DFO # inspectăm un fragment, din consolă # A tibble: 346 x 9 prof `1` `2` `3` `4` `5` `6` `7` zl 1 P01 10B 12D 8D 10A 12B - - Lu 2 P02 - 7E 11C 6D 7A 12E - Lu 3 P03 5D 8B - 8E 11C 6E - Lu
Primele 73 de linii din DFO reprezintă orarul zilei 'Lu', liniile 74:145 reprezintă orarul zilei 'Ma', ş.a.m.d. Pentru a evidenţia numai liniile care conţin ferestre, adăugăm o coloană $gps în care concatenăm valorile înscrise pe fiecare linie în coloanele `1`..`7`, eliminând însă (prin gsub()) valorile '-' iniţiale şi finale, dacă există; apoi, selectăm cu grep() numai liniile pe care în coloana $gps apare şi caracterul '-':
DFO$gps <- unlist(lapply(1:nrow(DFO), function(i) paste0(DFO[i, 2:8], collapse=""))) DFO$gps <- gsub('^-*|-*$', "", DFO$gps, perl=TRUE) WND <- DFO[grep('-', DFO$gps), ] > WND # inspectăm un fragment, din consolă (liniile zilei 'Lu') # A tibble: 61 x 10 prof `1` `2` `3` `4` `5` `6` `7` zl gps 1 P03 5D 8B - 8E 11C 6E - Lu 5D8B-8E11C6E 2 P05 9C 10E 12A - 11B 12D - Lu 9C10E12A-11B12D 3 P06 12E 9A - 5D 5E - - Lu 12E9A-5D5E 4 P07 8A 9C - 10E 5D - - Lu 8A9C-10E5D 5 P11 5B 6C 5A - 8F - - Lu 5B6C5A-8F 6 P13 10E - 10D 7D 8B - - Lu 10E-10D7D8B 7 P24 7C 6A - 6B 9D - - Lu 7C6A-6B9D 8 P29 12C 8E - 8A 10B - - Lu 12C8E-8A10B 9 P33 9A 10A - 9D - - - Lu 9A10A-9D 10 P45 - 7A - 7B 12C 7D - Lu 7A-7B12C7D
Am redat numai cele 10 linii cu ferestre, din ziua 'Lu'; fiindcă WND conţine 61 de linii şi fiindcă avem numai ferestre de câte o singură oră, în oricare zi – deducem că numărul total de ferestre ale orarului s-a redus de la cele 320 de ore existente iniţial (sau 233, fiindcă pentru 'Jo' şi 'Vi' am lucrat pe orarele obţinute prin alocarea inversă, începând cu profesorii cu ore puţine), la exact 61 de ferestre.
Iniţial, orarul nostru avea pentru ziua 'Lu' un număr de 65 de ferestre (16 de câte o oră, 17 de câte două ore şi 5 ferestre de câte 3 ore – v. [1]) şi iată – am reuşit să-l reformulăm încât să aibă numai 10 ferestre, toate de câte o singură oră. Dar este vorba de orarul obţinut prin programele din [1], plecând de la o încadrare reală a profesorilor, extrasă din orarul existent al unei anumite şcoli; oare pe orarul original de pe care am extras încadrarea, care o fi situaţia ferestrelor?
N-avem decât să repetăm secvenţa de comenzi de mai sus, asupra orarului original (după aducerea acestuia la formatul CSV cuvenit) şi obţinem:
> WND
# A tibble: 97 x 10
prof zi `1` `2` `3` `4` `5` `6` `7` gps
1 P01 Lu - - 10C - 8B 6A 11E 10C-8B6A11E
2 P04 Lu 7A 11B 6C - 6B 7C - 7A11B6C-6B7C
3 P05 Lu 10C - 12E 11E 9A 10D - 10C-12E11E9A10D
4 P07 Lu 8A - 5D - 12A 10E - 8A-5D-12A10E
5 P08 Lu 6D - 10A - - - - 6D-10A
6 P09 Lu - - 11A - 10E 11C - 11A-10E11C
7 P10 Lu 7E 10D 10D - 12B 12B - 7E10D10D-12B12B
8 P15 Lu 8E 6A 8E 8D - 8B - 8E6A8E8D-8B
9 P17 Lu 11B 11A - 10D - - - 11B11A-10D
10 P21 Lu 5D 10C - 12D 5D 7A 7A 5D10C-12D5D7A7A
11 P26 Lu 12D/12E - 5C 8C 11D/11E 11A/1… - 12D/12E-5C8C11D…
12 P28 Lu 12D/12E 5D - 8B 11C/11D… 5E 7D 12D/12E5D-8B11C…
13 P31 Lu 11D 10E 8B - 7D - - 11D10E8B-7D
14 P35 Lu 5E 5A 5B - 8F 6B 7B 5E5A5B-8F6B7B
15 P37 Lu 5A - 5E - 12E - - 5A-5E-12E
16 P42 Lu 10A 8C - 9D 6E 8C - 10A8C-9D6E8C
17 P48 Lu 10B - 7B 5B - - - 10B-7B5B
18 P52 Lu 8B 12D - 7B 10C - - 8B12D-7B10C
19 P54 Lu - - 12B - 12C - - 12B-12C
20 P55 Lu 9C 9A 6B 10E - 9B 9B 9C9A6B10E-9B9B
21 P56 Lu - - - 5A - 11D - 5A-11D
22 P57 Lu - - - 9C - 6D - 9C-6D
23 P58 Lu 8F - 6E - - - - 8F-6E
24 P67 Lu 9A 12A - 12A - - - 9A12A-12A
Am redat iarăşi, numai liniile corespunzătoare zilei 'Lu'. Se vede că pentru această zi, orarul original conţine 26 de ferestre (22 de câte o singură oră şi – la 'P07' şi 'P37' – două ferestre de câte două ore neconsecutive); în plus, 4 profesori (liniile 19 şi 21:23) au numai câte două ore, dar şi câte o fereastră între ele (situaţie pe care am reuşit să o evităm pe orarul nostru: în orice zi, cei cu numai două ore nu au fereastre).
WND conţine 97 de linii, dar între acestea avem şi 10 linii cu câte două ferestre – deci numărul total de ferestre pe orarul original este 107. Programul din [1] prin care am generat orarul nu prevedea vreo condiţie – de aceea au rezultat de două sau de trei ori mai multe ferestre (320 într-o versiune, 233 în cealaltă), decât în orarul original (şi de aceea, execuţia programului respectiv a durat aşa de puţin - 5 minute, respectiv 1 minut); probabil că dacă am reuşi să integrăm o condiţie prin care să se urmărească şi să se limiteze numărul de ferestre curent, am putea genera şi prin programul din [1], orare cu cel mult 100 de ferestre (cu preţul creşterii duratei de execuţie). Deocamdată am compensat absenţa unei astfel de condiţionări, prin aplicaţia („externă” programului) de reducere a ferestrelor, descrisă mai sus (bineînţeles că această aplicaţie se poate folosi şi pentru orarul original, reducând cele 107 ferestre probabil tot pe la vreo 60).
Perspectiva problemelor
Sunt cam trei luni, de când ne ocupăm aici de „problema orarului şcolar” (termen de căutare: "school timetabling problem"), folosind R. Am plecat de la o încadrare a profesorilor pe clase (câte ore şi la care clase, are fiecare); sunt două variabile „de completat”: ziua şi ora din zi, în care fiecare profesor să-şi facă lecţia la fiecare dintre clasele pe care este încadrat (sub condiţia principală de a nu suprapune lecţiile). Prin urmare, apar două probleme: repartizarea lecţiilor pe zilele de lucru şi respectiv, alocarea pe orele zilei a lecţiilor repartizate într-o aceeaşi zi
Trebuie observat că tratările teoretice întâlnite (v. "school timetabling problem") nu disociază aceste două probleme şi abordează problema ca fiind din clasa „probleme dificile” (de optimizare). Dar având două „variabile libere” – este normal să considerăm două probleme şi tratându-le separat, putem constata că pentru rezolvarea acestora nu este neapărat necesar să apelăm la tehnici sofisticate (dar subliniem că avem în vedere variabile libere, neconstrânse de la bun început).
Am rezolvat ambele probleme printr-un acelaşi algoritm, foarte simplu, „de etichetare” (bazat pe ideea de "factor" din R). Orice „lecţie” angajează în principal două date: un profesor şi o clasă; am „normalizat” datele încadrării (folosind pachetul R tidyverse) şi enumerând toate lecţiile într-o anumită ordine, am etichetat liniile respective prin factorul "Zile", respectiv (dar acum nu chiar factor) "Ora"-din-zi.
Etichetarea prin "Zile" decurge pe clase, asigurând deja, în mod implicit, că fiecare profesor îşi face lecţiile la o aceeaşi clasă în zile diferite (exceptând numai cazul când numărul acestor lecţii depăşeşte numărul zilelor de lucru). La repartizarea pe zile am impus acest principiu: lecţiile unui aceluiaşi profesor, la toate clasele sale, să fie repartizate echilibrat, dacă numărul total al acestora este cel puţin 10 (şi „îngrămădit” în două-trei zile, pentru profesorii cu puţine ore pe săptămână). Pentru retuşarea interactivă a repartizării pe zile obţinute prin programul respectiv, am creat aplicaţia /recast.
Având lecţiile dintr-o aceeaşi zi, repartizarea pe orele zilei decurge iarăşi, pe clase; liniile respective (cel mult 7, după numărul de ore pe ziua respectivă ale clasei curente) sunt etichetate cu o permutare sau alta a orelor, urmărind ca orele alocate astfel profesorilor clasei curente să nu se suprapună cu orele deja alocate anterior; coloana etichetelor respective este analogă coloanei "Zile", dar nu mai este un "factor" (trebuind să aibă un număr variabil de „nivele”, după câte ore are clasa curentă în acea zi).
Câtă vreme nu impunem vreo altă condiţionare pentru etichetarea cu ore, orarul zilei rezultă într-un timp foarte scurt, dar conţine multe ferestre; prin aplicaţia externă /dayRecast se pot reduce interactiv ferestrele existente pe orarul unei zile.
Am experimentat cele două programe de repartizare (pe zile, respectiv pe orele zilei) pe o încadrare destul de voluminoasă – 76 de profesori la 41 de clase, totalizând 1202 ore (sau „lecţii”) pe săptămână; din cele evidenţiate mai sus se poate aprecia că rezultatele finale sunt onorabile (atât ca timp total de lucru necesar obţinerii orarului final, cât şi în privinţa calităţii intrinseci a orarului), cu atât mai mult cu cât programele respective sunt şi foarte scurte (fiecare având sub 50 de linii de program, în limbajul R).
Unele aspecte au rămas totuşi, netratate – conducând la diverse noi probleme (ultimele două din lista care urmează, fiind cel mai importante):
— de văzut cum am putea reduce numărul de ferestre de pe orarul unei zile nu printr-o aplicaţie interactivă, ci automat, printr-un program independent;
— de integrat în programul mount_in_days.R o condiţionare prin care alocarea orară curentă să ţină seama de numărul de ferestre curent (defavorizând alocările care produc o creştere prea mare a acestuia);
— de creat (probabil în aplicaţia interactivă /dayRecast) posibilitatea de a muta o oră sau alta de pe orarul final al unei zile, pe orarul unei alte zile (reducând prin aceasta, numărul de ferestre şi pe o zi şi pe cealaltă);
— de văzut cum am putea completa programele din [1] (pentru generarea distribuţiei pe zile a orelor şcolii şi respectiv, pentru generarea distribuţiei pe orele zilei), încât să avem în vedere şi situaţia când o clasă trebuie partajată între doi profesori, sau când două clase trebuie combinate într-o aceeaşi oră a zilei;
— cum să adaptăm programele respective situaţiei în care clasele funcţionează în două schimburi (caz în care s-ar cuveni să fie cât mai puţine situaţii în care profesorul să aibă ore în ambele schimburi într-o aceeaşi zi).
Mai departe, dezvoltarea demarată prin [1] ar putea beneficia de colaborarea specifică proiectelor "open source"; rămâne de încercat cândva, „strângerea” lucrurile într-un "project" public de sine stătător…
vezi Cărţile mele (de programare)