Ajustări conjuncturale… de evitat (sau nu?)

În [1] am obţinut "distr_final.RDS" şi am zis că ar fi o distribuire acceptabilă pe zile, a orelor şcolii (având distribuţii individuale „cvasi-omogene”). Totuşi încă n-ar fi cazul să trecem la orarele zilelor (cum ziceam), fiindcă ne-a scăpat un aspect: numărul total de ore pe zi variază cam mult de la o zi la alta:

Dzl <- readRDS("distr_final.RDS")  # tibble 1202, <ord>prof <chr>cls <ord>zl
Zile <- c("Lu", "Ma", "Mi", "Jo", "Vi")
    # Total ore pe fiecare zi:
> unlist(lapply(Zile, function(z) nrow(Dzl[Dzl$zl == z, ])))
[1] 258 252 242 230 220

În [1], etichetarea cu zile a orelor şcolii decurge, clasă după clasă, în ordinea zilelor; deci numărul total de ore pe zi pentru fiecare clasă descreşte totdeauna de la prima zi (rezultând în total 258 de ore) spre ultima zi (cu 220 ore).

Este de prevăzut că (din mai multe puncte de vedere) generarea orarului pe o zi depinde şi de cât de încărcată este acea zi – încât pare o idee bună, redistribuirea pe zile a orelor din "distr_final.RDS", pentru a echilibra numărul total de ore pe zi.

Să listăm liniile claselor cu măcar o zi de 7 ore (numărul maxim de ore pe zi la clase):

hzc <- Dzl %>% group_by(cls, zl) %>% 
       count()  # n ore/zi, la fiecare clasă (41×5 = 205 linii |cls|zl|n|)

o7 <- hzc %>% filter(n == 7)  # numai liniile cu 7 ore

hzc %>% filter(cls %in% o7$cls) %>%  # liniile claselor cu măcar o zi de 7 ore
        spread(zl, n) %>% print(n=Inf)  # colonează după 'zl' valorile 'n'

           cls      Lu    Ma    Mi    Jo    Vi
         1 11C       7     6     6     6     6
         2 7A        7     7     6     6     6
         3 7B        7     6     6     6     6
         4 7C        7     7     6     6     6
         5 7D        7     7     7     6     6
         6 7E        7     7     6     6     6
         7 8A        7     7     7     6     6
         8 8B        7     7     7     6     6
         9 8C        7     7     6     6     6
        10 8E        7     7     6     6     6
        11 8F        7     6     6     6     6
        12 9B        7     6     6     6     6
        13 9D        7     7     6     6     6
        14 9E        7     6     6     6     6

Precizăm că prin spread() am trecut de la liniile cls|zl|n rezultate prin count() (41 clase × 5 zile = 205 linii), la forma tabelară tocmai redată (nivelele factorului $zl devin nume de coloane, iar valorile $n sunt mutate corespunzător pe aceste coloane).

În tabelul rezultat avem 26 de valori 7, cu distribuţia pe zile (14 9 3 0 0); să facem modificările necesare pentru ca distribuţia valorilor 7 să devină (6 5 5 5 5). Alegem 8 clase din tabelul de mai sus, la care să schimbăm între ele orele din ziua 1, cu cele din ziua 5 pentru 3 clase, respectiv cu orele din ziua 4 pentru alte 3 clase şi cu cele din ziua 3 pentru cele două clase rămase; alegem încă 4 clase la care să schimbăm între ele orele din ziua 2 cu cele din ziua 5 (la 2 clase), respectiv din ziua 4:

sht <- data.frame(cls = c("7A", "7C", "7E", "8C", "9D", "11C", "9B", 
                          "9E", "7D", "8A", "8B", "7E"),
                  z1 = c(rep(1, 8), rep(2, 4)),
                  z2 = c(4, 5, 5, 4, 4, 5, 3, 3, 5, 5, 4, 4))
for(i in 1:nrow(sht)) {
    D <- Dzl %>% filter(cls == sht[i, 1])  # liniile clasei curente
    z1 <- Zile[sht[i,2]]
    z2 <- Zile[sht[i,3]]
    D1 <- D %>% filter(zl == z1)  # subsetul etichetat cu 'z1', al clasei curente
    D2 <- D %>% filter(zl == z2)
    D1$zl <- z2  # în subset, etichetele 'z1' devin 'z2'
    D2$zl <- z1
    # transferă înapoi subseturile re-etichetate:
    Dzl[Dzl$cls == sht[i,1] & Dzl$zl %in% c(z1, z2), ] <- rbind(D1, D2)    
}

Prin aceasta, distribuţia numărului total de ore pe zi devine (250 248 244 235 225) – încă neechilibrată; repetând acelaşi procedeu de interschimbare şi pentru clase cu 6, 5 şi cu 4 ore pe zi putem ajunge la o distribuţia echilibrată (241 241 240 240 240).

Însă, producând asemenea modificări în "distr_final.RDS", vor fi afectate negativ distribuţiile individuale corespunzătoare profesorilor claselor angajate în procesul de interschimbare – rezultând distribuţii neomogene precum:

 P02  3  3  4  6  8
 P05  2  6  2  7  6
 P06  5  8  3  4  3
 P14  4  5  6  1  4

Am ales manual şi cam expeditiv, clasele cărora le-am interschimbat zile mai sus şi chiar nu-i de crezut că putem „programa” alegerea acestor clase în aşa fel încât să nu stricăm omogenitatea iniţială a distribuţiilor individuale. Prin urmare – odată ce am obţinut distribuţia cvasi-omogenă distr_final.RDS, acceptabilă cum ziceam – trebuie să evităm „ajustări” de genul celor întreprinse mai sus…

În schimb, putem completa aplicaţia interactivă /recast, asigurând ca opţiune şi posibilitatea de a regla numărul total de ore pe zi (caz în care trebuie să-i furnizăm nu un subset de ore, ci întreaga distribuţie a orelor). Anume, am adăugat o linie informativă pentru numărul total de ore pe zi la momentul curent (calculată după fiecare operaţie SWAP) şi… cam atât!

Am transformat întreaga distribuţie din distr_final.RDS în fişier CSV de forma celui obţinut prin funcţia make_df_sgr() în [1] numai pentru un subset de ore şi am introdus fişierul respectiv în /recast (în caseta <textarea>); apoi, am folosit operaţia Mark pentru fiecare clasă, împreună cu SWAP – mutând ore din zile cu 7 ore (respectiv, 6 ore sau 5 ore) la acea clasă în zile cu 6 ore (respectiv 5, sau 4 ore) – urmărind pe linia "Total:" cum variază distribuţia numărului total de ore pe zi. Bineînţeles că am mutat anumite ore, căutând să nu „stric” ci dimpotrivă, să îmbunătăţesc distribuţiile individuale pentru orele unora şi altora dintre profesori:

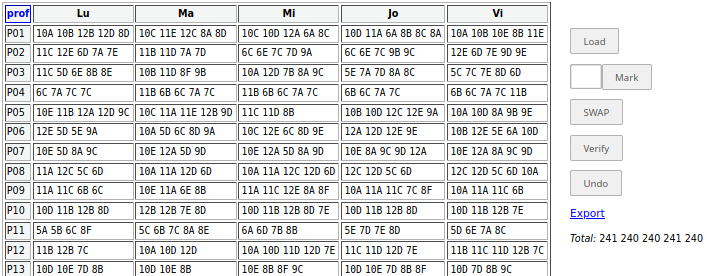
Spre deosebire de lucrul pe un subset de ore din [1], de data aceasta nu mi-a luat mai mult de o oră, ca să obţin o redistribuire a orelor "re_distr.cvs" (numele furnizat de operaţia "Export" din /recast) mult mai bună decât cea iniţială; acum distribuţia numărului total de ore pe zi este uniformă (cum se vede pe linia Total: în imaginea reprodusă mai sus), iar distribuţiile individuale sunt (aproape) toate, acceptabile (în privinţa omogenităţii şi a cazurilor de profesor cu puţine ore dar cu zile de o singură oră).

N-avem decât să reluăm programul renormal.R din [1] (IV), pentru a „normaliza” datele citite din "re_distr.cvs" şi a vedea apoi, matricea distribuţiei după clase şi pe cea a distribuţiei după profesor, a numărului de ore pe zi.

După ajustările întreprinse mai sus, vom lucra mai departe cu distribuţia de ore din "re_distr.cvs", în forma normalizată pe o salvăm acum în fişierul „final” "df1202x3.RDS" (abandonând "distr_final.RDS"); urmează într-adevăr, să trecem la „etapa II” – adică să ne gândim şi la orarul propriu-zis, al şcolii.