Dacă $\mathcal{E}$ desemnează o anumită curbă (sau chiar ecuaţia acesteia), putem obţine ecuaţia curbei rezultate prin rotirea acesteia în jurul originii cu unghiul $\theta$, făcând în ecuaţia $\mathcal{E}$ substituţia $x\rightarrow x\cos\theta+y\sin\theta$ şi $y\rightarrow y\cos\theta-x\sin\theta$. Într-adevăr, fie $R_\theta(x, y)=\left(x\cos\theta-y\sin\theta\,, y\cos\theta+x\sin\theta\right)$, rotaţia în jurul originii (în sens antiorar) cu unghiul $\theta$; dacă $(x,y)$ este un punct al curbei rezultate aplicând $R_\theta$ lui $\mathcal{E}$, atunci punctul lui $\mathcal{E}$ din care provine astfel $(x,y)$ este $R_\theta^{-1}(x,y)=R_{-\theta}(x,y)$ şi acesta (fiind pe $\mathcal{E}$) satisface ecuaţia iniţială (iar $\theta\rightarrow -\theta$ schimbă semnul lui $\sin\theta$, rezultând substituţia indicată).

Cu acest principiu, elipsa $\mathcal{E}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ se transformă prin $R_\theta$ în elipsa de ecuaţie $$\frac{(x\cos\theta+y\sin\theta)^2}{a^2}+\frac{(y\cos\theta-x\sin\theta)^2}{b^2}=1\quad\quad\quad(1)$$ (evident, tot o elipsă, fiindcă rotaţia păstrează distanţele). Focarele lui $\mathcal{E}$, $\pm(c,0)$ cu $c=\sqrt{a^2-b^2}$, sunt transformate în focarele elipsei rotite $\pm(c\cos\theta, c\sin\theta)$.

Din considerente de simetrie faţă de axe, putem presupune (asigurând simplificarea unor calcule) că $\theta\in[0,\frac{\pi}{2}]$; în fond, elipsele (1) pentru $\theta$ şi respectiv, $(\pi-\theta)$ sunt simetrice faţă de $\mathsf{O}y$.

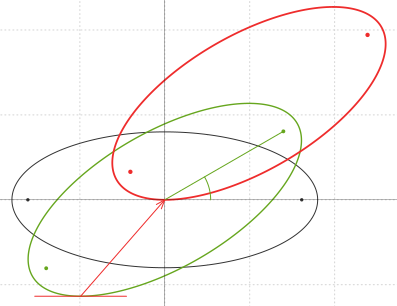Ce translaţie ar trebui aplicată lui (1), pentru ca elipsa rezultată prin aceasta să fie situată deasupra axei $\mathsf{O}x$ şi să fie tangentă în $\mathsf{O}(0,0)$ la $\mathsf{O}x$?

Dacă $\mathsf{T}$ este punctul lui (1) situat dedesubtul axei $\mathsf{O}x$ în care tangenta la elipsă este paralelă cu $\mathsf{O}x$, atunci translaţia căutată este dată de vectorul $\vec{\mathsf{TO}}$.

Pentru a determina punctul $\mathsf{T}$, cea mai elementară metodă ar fi probabil aceasta: vedem (1) ca ecuaţie de gradul doi în $y$ şi îi impunem condiţia de a avea o singură soluţie (dreapta $y=\lambda$ - paralelă cu $\mathsf{O}x$ - va fi tangentă la (1) dacă discriminantul ecuaţiei de gradul doi în variabila $y$ este zero); dar nu credem că aşa ar fi "cel mai simplu".

Preferăm să plecăm de la derivata lui (1) în raport cu $x$: $$\frac{2(x\cos\theta+y\sin\theta)(\cos\theta+y\,'\sin\theta)}{a^2}+\frac{2(y\cos\theta-x\sin\theta)(y\,'\cos\theta-\sin\theta)}{b^2}=0$$

Punând $y'\,=0$ (care exprimă condiţia ca tangenta în $\mathsf{T}(x,y)$ să fie paralelă axei $\mathsf{O}x$), ajungem la $$\frac{x\cos\theta+y\sin\theta}{y\cos\theta-x\sin\theta}=\frac{a^2\sin\theta}{b^2\cos\theta}\quad\quad\quad(2)$$

Împărţind în (1) prin numărătorul celei de-a doua fracţii şi folosind (2) (apoi, extrăgând radicalii) găsim: $$y\cos\theta-x\sin\theta=\pm\frac{b^2\cos\theta}{\sqrt{a^2\sin^2\theta+b^2\cos^2\theta}}\quad\quad\quad(3)$$ Acum, folosind (3) obţinem din (2) şi relaţia: $$y\sin\theta+x\cos\theta=\pm\frac{a^2\sin\theta}{\sqrt{a^2\sin^2\theta+b^2\cos^2\theta}}\quad\quad\quad(4)$$

Soluţiile $(x,y)$ ale sistemului de ecuaţii format de (3) şi (4) se citesc aproape imediat dacă folosim "regula lui Cramer"; dintre cele două soluţii, cea care reprezintă punctul $\mathsf{T}$ aflat dedesubtul axei $\mathsf{O}x$ este aceea pentru care $y$ este negativ: $$x_{\mathsf{T}}=-\frac{(a^2-b^2)\sin\theta\cos\theta}{\sqrt{a^2\sin^2\theta+b^2\cos^2\theta}},\quad y_{\mathsf{T}}=-\sqrt{a^2\sin^2\theta+b^2\cos^2\theta}\quad\quad\quad(5)$$

A aplica lui (1) translaţia de vector $\vec{\mathsf{TO}}$ revine la a face în (1) substituţiile $x\rightarrow x-x_{\mathsf{T}}$ şi $y\rightarrow y-y_{\mathsf{T}}$; rezultă că ecuaţiile elipselor tangente în $\mathsf{O}$ axei $\mathsf{O}x$ şi situate deasupra lui $\mathsf{O}x$ sunt: $$\frac{\left((x-x_{\mathsf{T}})\cos\theta+(y-y_{\mathsf{T}})\sin\theta\right)^2}{a^2}+\frac{\left((y-y_{\mathsf{T}})\cos\theta-(x-x_{\mathsf{T}})\sin\theta\right)^2}{b^2}=1\quad\quad\quad(6)$$ unde $x_{\mathsf{T}}$ şi $y_{\mathsf{T}}$ sunt date de (5), iar $\theta\in[0,\pi]$.

(6) este o expresie de forma $Ax^2+Bxy+Cy^2+Dx+Ey+F=0$. Pentru calculul coeficienţilor $D$, $E$ şi $F$ avem de ţinut seama de (5); dar $D$ şi $F$ trebuie să fie zero şi nu-i cazul să-i mai calculăm (ecuaţia tangentei în origine se obţine anulând partea de grad minim $Dx+Ey+F=0$, iar aceasta coincide cu $y=0$ dacă $F=D=0$). Calculând separat coeficienţii lui $x^2$, respectiv $xy$, $y^2$ şi $y$ şi eliminând în final numitorul $a^2b^2$, ajungem la această reformulare a lui (6):

Elipsele din semiplanul superior tangente în $\mathsf{O}$ axei $\mathsf{O}x$ sunt $Ax^2+Bxy+Cy^2+Ey=0$ cu $$\begin{array}{@{}cll} A &=& a^2\sin^2\theta + b^2\cos^2\theta \\ B &=& -(a^2-b^2)\sin 2\theta \\ C &=& a^2\cos^2\theta + b^2\sin^2\theta \\ E &=& -2a^2b^2 / \sqrt{A} \\ \end{array}$$ unde $a$ şi $b$ sunt semiaxele (cu $b\le a$), iar $\theta\in[0,\pi]$; pentru fiecare triplet de valori $(a,b,\theta)$ rezultă câte una dintre elipsele menţionate. Aceste elipse au centrele $(x_c=-0.5B/\sqrt{A},\,y_c=\sqrt{A})$, iar focarele lor sunt $(\pm\sqrt{a^2-b^2}\cos\theta+x_c,\, \pm\sqrt{a^2-b^2}\sin\theta+y_c)$.

Desigur, pentru a determina centrele am ţinut seama de faptul că $\mathsf{O}(0,0)$ (care este centrul elipsei (1)) ajunge prin translaţia de vector $\vec{\mathsf{TO}}$ în punctul $(x_c=-x_\mathsf{T},\,y_c=-y_\mathsf{T})$.

Validăm cele de mai sus producând graficele corespunzătoare, prin următorul program R:

require(randomcoloR)  # oferă palete cu numărul dorit de culori distincte
pall <- randomcoloR::distinctColorPalette(12)

plot_path <- function(func2, ...) {  # funcţie generică pentru a plota f(x,y)=0
    u <- seq(-1.5*a, 2*a, by=0.01)
    v <- seq(-1.5*a, 2*a, by=0.01)
    Z <- outer(u, v, func2)  # valorile f(u,v), indexate după u şi v
    contour(u, v, Z, levels = c(0), drawlabels=FALSE, add=TRUE, ...)
}

elli <- function(x, y) {  # ecuaţia elipsei, cu (a,b,h) fixat dinafară (global)
    A <- a^2*sin(h)^2 + b^2*cos(h)^2
    B <- -(a^2-b^2)*sin(2*h)
    C <- a^2*cos(h)^2 + b^2*sin(h)^2
    E <- -2*a^2*b^2/sqrt(A)  #; print(c(A, B, C, E))
    A*x^2 + B*x*y + C*y^2 + E*y
}

draw_ell <- function(a=4, b=1.5, theta=NULL, kol=pall) {
    plot(0, type="n", asp=1, bty="n", xlab="", ylab="", xaxt="n", yaxt="n",
         xlim=c(-2*a, 2*a), ylim=c(0, 2*a)); grid()  # setează fereastra grafică
    a <<- a; b <<- b;  # creează copii globale pentru variabilele 'a' şi 'b'
    k <- 1  # index în paleta de culori
    if(is.null(theta)) {
        theta <- seq(0, pi, by=pi/10)  # o secvenţă convenţională de unghiuri
    } else {
        if(!is.vector(theta)) theta <- as.vector(theta)
    }
    if(!is.vector(kol)) kol <- as.vector(kol)
    for(h in theta) {
        h <<- h  # exportă variabila 'h'
        plot_path(elli, col=kol[k], lwd=1.4)  # plotează elipsa cu parametrii (a,b,h)
        yc <- sqrt(a^2*sin(h)^2 + b^2*cos(h)^2)
        xc <- (a^2-b^2)*sin(h)*cos(h) / yc
        points(xc, yc, pch=19,cex=0.6, col=kol[k])  # centrul elipsei
        f <- sqrt(a^2-b^2)
        F1 <- f*exp(1i*h) + (xc + 1i*yc)
        F2 <- -f*exp(1i*h) + (xc + 1i*yc)
        points(c(F1, F2), cex=0.6, col=kol[k])  # focarele elipsei
        k <- k+1 
    }
    abline(h=0, lwd=0.4)  # tangenta elipselor, în origine
}

draw_ell()  # prima figură
# draw_ell(a=9, b=4, theta=c(pi/6, 5*pi/6), kol=c("blue", "red"))  # figura din dreapta sus
# draw_ell(a=2, b=1, theta=pi/3, kol="darkgreen")  # figura din dreapta jos

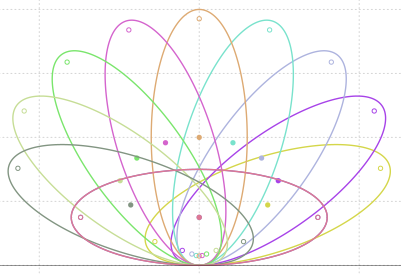
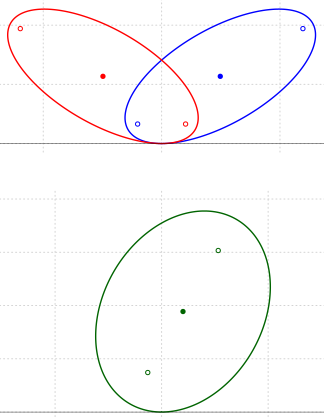
În figura din stânga (obţinută prin apelul draw_ell()) avem 10 elipse (6), cu aceleaşi semiaxe a=4 şi b=1.5, pentru $\theta$ (reprezentat în program prin variabila 'h') multiplu de $\pi/10$. Panoul din dreapta redă în partea de sus a sa două elipse (6) simetrice faţă de $\mathsf{O}y$ (obţinute prin apelul comentat pe penultima linie a programului), cu aceleaşi semiaxe a=9, b=4 şi cu $\theta=\pi/6$, respectiv $\theta=5\pi/6$; în partea de jos a panoului, avem elipsa (6) corespunzătoare apelului comentat pe ultima linie a programului.

Obs. Faptul că am putut apela funcţia draw_ell() şi cu parametri scalari ('theta=pi/3' - v. ultima linie, comentată, din program) şi cu parametri vectoriali ('theta=c(pi/6, 5*pi/6)') a fost asigurat prin folosirea în program a testului is.vector() (dacă rezultatul este "FALSE", atunci am transformat valoarea scalară transmisă folosind as.vector()).
Obs. Fiindcă sunt deja vreo trei ani de când folosim frecvent R pe acest site (cu explicaţii şi cu diverse programe ilustrative), considerăm că aici nu mai este cazul de a "diseca" mai mult, programul redat mai sus.

Am plotat centrele (punctele "pline") şi focarele (punctele "cerculeţ"), pentru a sugera unele chestiuni care se ridică în mod firesc pentru elipsele (6). Care este locul centrelor şi locul focarelor, când păstrând constante semiaxele, variem $\theta$? Dar când variem după vreo anumită regulă şi semiaxa $b$? Etc.

În [1] am formulat o "concluzie" care acum este clar că ar trebui îngustată: "Elipsele cu axa mare de o aceeaşi lungime şi care sunt tangente într-un acelaşi punct $\mathsf{O}$ unei aceleiaşi drepte $d$, au centrele pe două arce de parabolă simetrice faţă de perpendiculara în $\mathsf{O}$ pe $d$ şi au focarele pe două cardioide care au nodul în $\mathsf{O}$, au axa pe $d$ şi sunt simetrice faţă de perpendiculara în $\mathsf{O}$ pe $d$".
Elipsele despre care era vorba în [1] (a căror ecuaţie analogă cu (6), o deduceam pe cu totul altă cale decât aici - anume, plecam de la o anumită parametrizare a focarelor) constituie de fapt a anumită sub-familie (strictă) a celor definite de ecuaţia generală (6); este de văzut ce relaţii avem între variabilele ($a, b, \theta\,$) din (6) şi parametrul $t\in[0,\frac{1}{2}]$ pe baza căruia formulam în [1] ecuaţiile respective (şi… "va urma", sperăm).