contourLevels() (din R) primește diviziunile de axe, X și Y, precum și vectorul Z în care s-au calculat în prealabil (de obicei, prin outer()), valorile f(x,y) în punctele rețelei X×Y și returnează o listă în care sunt înregistrate pentru fiecare nivel λ dintre cele indicate, câte unul sau mai multe contururi (sau segmente de curbă) care împreună, ar forma curba de nivel λ (intersecția suprafeței de ecuație z=f(x,y) cu planul z=λ).

În [1] am constituit funcția plot_contours(), pentru a trasa toate contururile înregistrate în lista H de către contourLevels() (evidențiind prin culoare, contururile de pe nivelul zero, dacă s-au indicat mai multe niveluri); dar, cu graba obișnuită — de obicei nerecomandată — de a formula concis, s-a strecurat totuși o greșală copilărească, la calculul limitelor contururilor existente:

    Lim <- sapply(1:length(H), function(i) 
                  c(range(H[[i]]$x), range(H[[i]]$y)))

ne dă o matrice cu 4 linii și length(H) coloane — deci calculul limitelor pe $Ox$ și $Oy$ prin range(Lim[, 1]) și respectiv range(Lim[, 2]), prevăzut în formularea "concisă" din [1], este greșit: se vizează numai primele două coloane și se reține minimul și maximul de pe fiecare (fără a mai ține seama că pentru abscise trebuie considerate numai primele două valori din coloană, iar pentru ordonate, celelalte două). S-a întâmplat pentru exemplificările din [1], că valorile extreme din primele două coloane erau suficient de potrivite, așa că n-am sesizat când s-ar fi cuvenit, această greșală…

Îndreptarea necesară nu-i greu de făcut și numai pentru atâta, nu-i de încropit vreun articol; poate am mai complica puțin codul respectiv, pentru a plota în culori diferite curbele de pe nivelurile indicate (ceea ce nu este banal decât dacă în H avem câte un sigur contur, pentru fiecare nivel). Dar bineînțeles că tot n-ar ajunge…

Să "complicăm" lucrurile: pentru a folosi comod funcția plot_contours() (fără ajustări ad-hoc), s-ar cuveni să o împachetăm (v. [2]). Va rezulta un pachet poate nu chiar banal, dar fără valențe de publicare; profităm totuși de prilej, ideea fiind că pentru a nu uita (cum se face un pachet R), trebuie să exersezi… (de fapt, ideea și necesitatea proprie de a construi acest pachet, a izvorât studiind o anumită curbă, în [3]).

Funcționalitatea de asigurat

Înainte de a demara construcția pachetului, trebuie să ne gândim la circumstanțele în care l-am folosi și să decidem ce componente ar trebui constituite; aceasta este de fapt, partea esențială a lucrurilor (în rest… folosim devtools).

În forma inițială (v. [1]), plot_contours() primește numai H, matricea returnată de un apel prealabil contourLevels() (ignorăm argumentul auxiliar "...", în care poate primi valori de parametri grafici, spre a-i pasa funcțiilor de plotare pe care le invocă în interiorul său) — și… face "toate-cele": inițializează fereastra grafică, astfel încât să acopere toate coordonatele reprezentate în H, iar apoi plotează (apelând lines()) fiecare dintre contururile înregistrate în H, impunând o culoare pentru contururile de pe nivelul zero și o alta, pentru toate celelalte nivele.

Însă dacă există deja o fereastră grafică, inițializarea ferestrei grafice în interiorul plot_contours() va șterge conținutul acesteia; poate că s-ar vrea adăugarea contururilor, peste graficul existent. Deci "inițializarea" s-ar cuveni să fie opțională.

Dacă utilizatorul a indicat mai multe niveluri, atunci probabil că acestea sunt semnificative; s-ar cuveni să prezentăm distinct în privința culorii, curbele de nivel respective (cu o "legendă" opțională).

Nu-i cazul să ne gândim acum, la "amănunte"; dar iată unul: cine ar vrea să adauge curbele de nivel în fereastra existentă (deci va invoca plot_contours() fără "inițializare"), va trebui să se asigure cumva că limitele de axe existente convin și curbelor de nivel.

Demersurile obișnuite pentru crearea unui pachet

Prin pak::pkg_name_check("plotlev") verificăm dacă numele de pachet pe care l-am ales este valid. Apoi încărcăm pachetul devtools, ale cărui funcții le vom folosi pentru dezvoltarea pachetului propriu; prin create_package("plotlev") rezultă subdirectorul plotlev/ în care, pe lângă fișiere descriptive ("DESCRIPTION", "NAMESPACE", "LICENSE"), găsim un subdirector R/ în care urmează să înscriem funcțiile R ale pachetului.

În cazul de aici nu avem dependențe de alte pachete, așa că nu prea avem de făcut completări în fișierele descriptive furnizate (este necesară însă, precizarea unei "licențe" — ceea ce se poate expedia imediat prin funcția use_mit_license()).

use_r("<nume_funcție>") creează în plotlev/R/ un fișier cu numele indicat, în care avem de editat corpul funcției respective — respectând însă un anumit format de documentare. Avem de folosit din când în când, cam în această ordine, funcțiile document() pentru a verifica starea documentației la momentul curent, load_all() care încarcă pachetul (fără să-l instaleze în sistem) și check(), care verifică "toate-cele" și semnalează eventualele erori; în final, dacă check() nu produce vreo notificare, pachetul creat astfel poate fi instalat, apelând install().

Problema limitelor (unui ansamblu de vectori numerici)

În plot_contours() vizasem precis, matricea rămasă dintr-un apel prealabil contourLines(); dar problema de a determina valorile extreme ale unui set de vectori este una generală și o tratăm în funcția get_limits():

#' Limitele necesare plotării unor segmente de curbă (contururi)
#' @param H  listă de contururi, pe nivele
#'     Pe un nivel pot exista mai multe contururi;
#'     pentru fiecare contur sunt înregistrate coordonatele (x, y) 
#' @return  lista valorilor extreme ale absciselor și ordonatelor
#' @export
#'
#' @examples
#' H <- list(list(x=0:10, y=-5:5))
#' rangeXY <- get_limits(H)
#' plot(H[[1]])  # se poate, având același număr de abscise și ordonate
#' 
#' H <- list(list(x = 2*rnorm(10), y = 2*rnorm(10), lev=0), 
#'            list(x = 2*rnorm(5), y = 2*rnorm(5), lev=1))
#' rangeXY <- get_limits(H)
#'
get_limits <- function(H) {
    Nq <- length(H)
    Lim <- sapply(1:Nq, function(j) 
                  c(range(H[[j]]$x), range(H[[j]]$y)))
    if(Nq == 1)  # când Lim poate fi un vector, nu o matrice  
        dim(Lim) <- c(4, 1)
    list(xlim = range(Lim[1:2, ]), ymin = range(Lim[3:4, ]))
}

Am redat chiar textul înscris în fișierul R/get_limits.R (exceptând un al treilea "exemplu", la care ne vom referi mai jos). Sensul "documentării" (liniile prefixate prin "#'") constă în aceste aspecte: după ce utilizatorul va fi instalat pachetul, va putea folosi funcția plotlev::get_limits() (datorită declarației @export); prin help(get_limits) va putea vedea documentația aferentă; prin example(get_limits) va putea rula exemplele de sub declarația @examples.

Exemplele redate mai sus sunt (cum și trebuie) banale; în al doilea, am generat (prin rnorm()) secvențe aleatorii de abscise și ordonate (într-o listă de liste, care pot conține și alte câmpuri, de exemplu "lev") și am determinat prin get_limits() valorile extreme. Un al treilea exemplu este mai interesant, fiindcă ne apropie de funcționalitatea de bază a pachetului — lucrând însă direct, fără outer() și contourLines():

 circle <- function(x, y) x^2 + y^2 - 4
 X <- Y <- seq(-2.5, 2.5, length=600)
   ## valorile f(x,y) în toate punctele rețelei XxY
 DF <- expand.grid(x = X, y = Y)
 DF$z <- circle(DF$x, DF$y)
   ## selectăm (x, y) pentru care f(x, y) este suficient apropiat de 0
 DF <- DF[abs(DF$z) < 0.01, ]
 H <- list(list(x = DF$x, y = DF$y))  ## lista de contururi (unul) 
 rangeXY <- get_limits(H)
 plot(H[[1]], pch=16, cex=0.4, asp = 1)

Am considerat o funcție f(x,y) (aici, definind un cerc, dacă vizăm nivelul 0) și două diviziuni pe axe, X și Y. Prin expand.grid() obținem un "tabel" DF care împerechiază fiecare x∈X cu fiecare y∈Y; adăugăm în DF o a treia coloană, conținând valorile z=f(x,y). Apoi, reținem din DF numai liniile pentru care în coloana z avem valori cât mai apropiate (aici, la o sutime) de zero și obținem lista H a coordonatelor aproximate pentru punctele curbei f(x,y)=0; get_limits() ne dă limitele acestor coordonate (iar imaginea produsă în final prin plot() le va și confirma).

Obs. Este de comparat lista H rezultată "direct" (instituind și manevrând un data.frame DF), cu lista H care ar rezulta folosind contourLines(); mai ales în cazul când X, Y, Z sunt variabile statistice asociate unui set de date (nu ca aici, asociate unei funcții analitice f(x,y)), este de așteptat să existe diferențe semnificative între valorile conținute — dat fiind că în contour() și în contourLines() se aplică un anumit algoritm (sofisticat), pentru o cât mai bună estimare a contururilor (analizând și mediind pe vecinătăți, punctele (x,y,z)).

Problema colorării după nivel a contururilor

Înscriem în R/col2lev.R funcția următoare, prin care se asigură o posibilitate de a colora cu o aceeași culoare contururile de un același nivel, distinct de la un nivel la altul:

col2lev <- function(H) {
    vlc <- vapply(H, `[[`, 1, "level") # nivelul fiecărui contur
    id0 <- which(vlc == 0)  # indecșii contururilor nivelului 0
    # un set aleatoriu de culori, câte una pentru fiecare nivel
    Dc <- grDevices::colors()
    Kol <- Dc[grep('gr(a|e)y|light|white|black', Dc, invert = TRUE)] |>
           sample(size = length(table(vlc)))
    # "colorează" contururile fiecăruia dintre nivele
    cols <- factor(vlc, labels = Kol) |> as.vector()
    cols[id0] <- "black"  # pentru curba de nivel 0
    cols
}

Prin vapply() am obținut un vector care conține valoarea "level" înregistrată fiecărui contur (în ordinea acestora din lista H); pentru argumentul "FUN" am indicat (sub backtick) operatorul de indexare "[[" (adăugând apoi un șablon numeric (fie 1) pentru valorile "level" cerute).
Prin which() am reținut într-un vector, indecșii contururilor de nivel 0 — în ideea de a fixa culoarea "Black" pentru curba de nivelul 0 (de bază, când studiem o curbă de ecuație f(x,y)=0).
colors() furnizează un vector conținând vreo 650 de nume de culori; prin grep() (cu argumentul invert) am eliminat "white", "black", precum și vreo sută de culori al căror nume conține "gray", "grey", sau "light"… Dintre culorile rămase am selectat aleatoriu (prin sample()), un număr de culori egal cu numărul de nivele (obținut prin table()). Subliniem că existau și soluții mai bune, folosind de exemplu pachetul RColorBrewer — dar am vrut să folosim numai pachetele de bază.
În final, prin factor() am asociat fiecărui contur culoarea corespunzătoare câmpului level al acelui contur (schimbând însă în "Black", culoarea asociată nivelului 0) și am returnat vectorul de culori astfel constituit.

Ordinea culorilor în vectorul K returnat este aceeași cu ordinea contururilor din lista H, încât vom putea folosi lines(H[[j]], col=K[j]), pentru a plota colorat după nivel, fiecare contur înregistrat în H.

Ca exemplu (al cărui text nu-l mai redăm aici), am considerat o listă H conținând 6 contururi foarte simple, imaginând câte două "curba" formată de o pereche de paranteze:

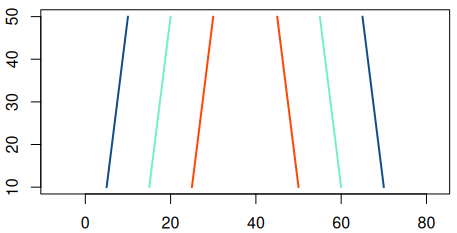
Avem deci trei paranteze "((( )))", iar acesta au fost colorate distinct, după nivelul de imbricare al lor (invocând desigur col2lev()).

Pentru a produce imaginea de mai sus am folosit desigur și funcția constituită anterior get_limits() — prilej cu care ne-am dat seama că era mai bine ca aceasta să returneze nu o listă (de câmpuri "xlim" și "ylim"), ci (direct) o matrice 2x2:

    cbind(range(Lim[1:2, ]), range(Lim[3:4, ]))

Bineînțeles că am operat această modificare (inclusiv pentru documentarea cuvenită sub "@return", în R/get_limits.R), dar n-am revenit aici, asupra textului redat mai sus…
Trebuie să fie clar: constituirea unui pachet nu poate decurge liniar.

Obs. Vizăm aici un pachet "local" (de integrat pe "sistemul meu"), așa că nu prea luăm seama la fișierele descriptive; altfel, ar trebui să observăm de exemplu, că mai sus am folosit operatorul "pipe" '|>', introdus începând cu versiunea R 4.1 — încât trebuie precizată restricția respectivă, în fișierul "DESCRIPTION" (sub descriptorul "Depends:").

Problema finală: plotarea curbelor de nivel

În R/plot_contours.R introducem funcția următoare (dar aici o redăm ca atare, fără documentarea asociată):

plot_contours <- function(H, init_wnd = TRUE, ...) {
    if(init_wnd) {
        plot.new()
    	plot(get_limits(H), type = "n", asp = 1, 
    	     bty="n", xlab="", ylab="", ...)
    }
    cols <- col2lev(H)
    for(j in 1:length(H))
        lines(H[[j]]$x, H[[j]]$y, col = cols[j], ...)
}

Dacă există deja o fereastră grafică și utilizatorul vrea să-i adauge rezultatul produs acum de plot_colours(), atunci va trebui să o apeleze folosind init_wnd=FALSE.
În argumentul "..." se vor putea specifica diverși parametri grafici, dar alții decât cei deja fixați în plot() și lines().

Când am lucrat mai sus get_colours(), check() ne-a atenționat că nu putem folosi colors() decât indicând într-un fel sau altul, pachetul din care provine — și atunci am folosit construcția grDevice::colors(). La fel acum, check() atenționează asupra funcțiilor plot() și lines(); de data aceasta am folosit use_import_from(), pentru a indica în fișierul "NAMESPACE" că aceste funcții provin din pachetul (de bază) graphics.

Fiindcă în final check() nu a mai produs vreo notificare, putem folosi install, obținând posibilitatea de a folosi pachetul plotlev la fel cum folosim oricare alt pachet R — dar numai de pe calculatorul propriu (de unde s-au prelucrat în vederea instalării, fișierele-sursă respective).

Ca exemplu, constituim într-un director oarecare acest program, în care importăm pachetul plotlev, considerăm o funcție f(x,y) și diviziunile pe axe X și Y, apoi obținem (prin outer()) valorile Z=f(x,y), obținem prin contourLines() lista H a contururilor și le plotăm prin plotlev::plot_contours():

library(plotlev)
FUN <- function(x, y)
    (x^2+y^2)^4 - 3*(x^2+y^2)^2 - 2*(x^2-y^2)  # curba "nah_Dürer"
X <- Y <- seq(-2, 2, length=1000)    
Z <- outer(X, Y, FUN)
H <- contourLines(X, Y, Z, levels = seq(-1, 0.5, by=0.25))
plot_contours(H, lwd = 1.1)

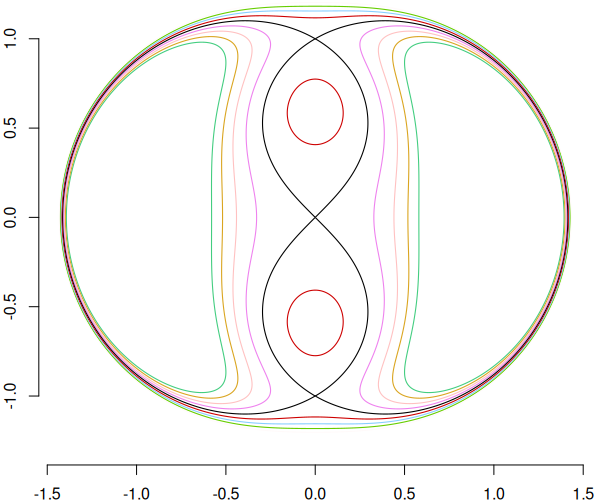
Curba de nivel 0 (colorată "Black") a fost introdusă în [3]; inspectând lista H, constatăm că îi corespund trei contururi. Avem tot trei contururi și pentru curba colorată cu nuanță pronunțată de "maroon" (sau "red"?), constând din cele două ovale interioare buclelor curbei de nivel 0 și un "oval" exterior acesteia (dar vor fi alte culori, dacă repetăm execuția programului…).

Sesizăm, repetând execuția programului, că apar cel mai frecvent culori palide… Dacă ar fi s-o luăm de la capăt, am defini un set constant de vreo 15 culori dintre cele mai pronunțate, bine distincte între ele (și o funcție publică pentru a le reda la cerere) și am alege (aleatoriu) culorile pentru contururi pe baza acestuia (iar pentru cine ar cere mai mult de 15 nivele… am folosi o aceeași nuanță de gri, pe lângă setul de 15 culori).