Cu [1] beneficiem, din partea D-lui Prof. dr. Ioan Pop (Univ. "Al.I.Cuza", Iași), de o lecție generoasă despre "funcții implicite" (și "curbură"), cu aplicație la reprezentarea grafică ("umană") a ovalelor lui Cassini (în patru cazuri tipice); scopul lecției este superb: "când vedem desenul făcut de calculator, chiar să înțelegem de ce este așa".

Noi înțelegem acest scop așa: partea esențială a lucrurilor, care este neliniară și umbrită de îndoieli, constă în a înțelege, a asimila și poate a reformula (de exemplu, când le-am vedea exprimate cumva, vizual) noțiunile și legăturile acestora; în rest… putem instrui cumva calculatorul ("ne-uman"), să concretizeze demersurile respective (pentru asta s-a inventat acest instrument: ne mai scutește, după cum îl instruiești, de a efectua noi înșine — mereu și de la caz la caz — calculele necesare finalizării lucrurilor).
Așa înțelegând, ajungem să ne confruntăm și cu un al doilea scop, iarăși superb: când vedem programul care a produs desenul, chiar să înțelegem cum a rezultat acesta…

În [2] se pleacă de la un cerc care trece prin origine și se evidențiază că radicalul acestuia (în $\mathbb{C}$) este o lemniscată Bernoulli… Acum vom evidenția că "radicalul unui cerc oarecare este un oval Cassini", asigurând astfel o punte de legătură cu [1].

Tratarea directă

A trata "uman" lucrurile înseamnă, cum se zice în [1], a justifica "alura și punctele importante ale adevăratei curbe" (avem de știut și de ținut seama de "teorema de existență a funcțiilor implicite" și de "încă un ingredient", curbura). Iar "adevărata curbă"… este aceea pe care nimeni, nici calculatorul, n-o poate trasa cu exactitate.
Dar aceasta nu înseamnă că trebuie să excludem posibilitatea de a folosi vreun instrument de calcul simbolic… Cu SageMath putem exprima / expanda ușor diversele formule de care avem nevoie pentru a desena curba "prin metoda învățată în liceu" (reducând spre ridicol, teama că vom fi greșit undeva, inerentă calculului manual).

Plecăm de la funcția implicită care caracterizează curbele lui Cassini (v. [1]):

(neimportant: avem $a$ și $b$, în loc de $c$ și $a$; $b^4$ pare mai lizibil versus $c^4$ și $a^4$)

Ilustrăm aici cum putem folosi fiecare (din browserul propriu) SageMath (se cuvine să precizăm: pe imaginea redată aici am exclus sigla "SageMathCell" de la începutul paginii):

Bineînțeles că era ușor de data aceasta, să facem manual înmulțirile și simplificările (verificând de câte două ori, ca să fim siguri că n-am greșit…); folosind formatul LaTeX furnizat, redăm forma expandată obținută astfel pentru $F(x,y)$:

Să facem măcar acum (că se cuvenea deja de la (1)) niște "observații umane" importante: fiindcă $x$ și $y$ apar numai la puteri pare, avem $F(x,y)=F(\pm\, x,\, \pm\, y)$; altfel spus… ne-am putea scuti de a încărca inutil discuția și figurile — e absolut suficient să ne referim la secțiunea din primul cadran, a curbelor.
Mai putem observa că dacă $a=b$, atunci $F(x,y)=F(y,x)$, adică în acest caz avem simetrii și față de bisectoarele sistemului de axe…

Folosind (2) găsim imediat expresiile derivatelor parțiale (dar dacă vrem, le putem obține și în SageMath: F.diff(x) ne-ar da expresia derivatei după $x$):

Din teorema funcțiilor implicite avem derivata $f'$ a acelei funcții $y=f(x)$ pentru care $F(x,f(x))=0$, anume:

Este de subliniat (ca și în [1]) că (4) ne dă $f'(x)$ (panta tangentei) în punctele $(x,y)$ ale curbei (pentru care $F_y(x,y)\ne 0$) în funcție de coordonatele respective — deci fără a ști funcția (explicită) $f$ pentru care $y=f(x)$.

Vom avea nevoie și de $f''$, iar de data aceasta chiar preferăm să folosim SageMath:

Iar pentru raza cercului osculator într-un punct al curbei (v. [1]), avem:

N-am mai redat expresiile simbolice (foarte lungi) produse de SageMath, fiindcă de fapt, nu vom avea nevoie de ele: primele patru formule de mai sus sunt suficiente pentru a determina pentru valori concrete $a$ și $b$, elementele caracteristice ale curbelor, iar apoi pentru a calcula (5) și (6) putem folosi direct rezultatele din (3) și (4), în loc de a determina intermediar, expresiile acestora (în termenii $\mathrm{var}(x, y, a, b)$).

De-acum discuția poate decurge după tipicul obișnuit manualului de liceu: determină intersecțiile cu axele de coordonate (și apar două sau trei cazuri, după cum se raportează între ele valorile $a$ și $b$); determină punctele în care avem tangente paralele cu $Ox$ (și apare un caz interesant, în care curbele respective au două bitangente), respectiv cu $Oy$; determină dacă există, punctele de inflexiune (bineînțeles că e suficient să le găsim pe cele din primul cadran); vezi cumva punctele în vecinătatea cărora curba diferă cel mai puțin, respectiv cel mai mult, de un cerc (aici va fi necesară $f''$ și formula (6)); reprezintă grafic, pentru diverse cazuri $a$ și $b$, secțiunea curbei aflate în primul cadran (și apoi, simetrizează față de axe).
Și în plus… determină aria subgraficului din primul cadran și volumul corpului de rotație corespunzător (apoi înmulțești cu 4, respectiv cu 2…). Este de observat că această ultimă cerință depășește până la urmă, domeniul elementar (ține de "integrale eliptice") — dar ar putea fi totuși "rezolvată" folosind SageMath…

Am putea desfășura aici, pe vreo două pagini, calculele și divagările pe cazuri descrise mai sus; dar ce am câștiga (afară de faptul că am mai învăța să scriem) și ce ar mai câștiga cine ar citi ? Altfel putem fi de acord că "Munca are valoare în sine"…

Instruirea calculatorului…

Intenționăm să nu folosim SageMath decât pentru lucruri mai obișnuite: expandarea vreunei formule, calculul expresiilor unor derivate sau primitive, etc. (altfel, SageMath vizează interesele profesioniștilor și cercetătorilor specializați pe diverse domenii avansate din matematică, fizică, informatică, etc.); în treacăt fie zis, am instalat sursele SageMath pe calculatorul propriu — a durat cam patru ore. De!… "munca are valoare în sine"; dar altfel (permițându-ne o notă de "luare-aminte", din care și decurge, intenția cuminte și cinstită enunțată mai sus): parcă nu mai este timp să recuperezi ceea ce ai ratat atâția ani, ca să te ridici la o situație în care ai putea eventual să beneficiezi de valențele investigative din Sage ("System for Algebra and Geometry Experimentation".

Vom folosi ca de obicei, limbajul R — cu pachetul tidyverse și având mereu ca "ingrediente", editorul de text gedit pentru a scrie programele și consola R pentru lucrul interactiv; ca de obicei, constituim programe R, conform specificațiilor strecurate implicit mai sus și totodată, îngemănat, continuăm să scriem (și să rescriem de la început, în alte vreo câteva zile) textul HTML al articolului de față (care ar fi "gata" cam atunci când n-aș mai vedea ceva… de eliminat).

De fapt… am putea obține graficul imediat, fără "marafeturi" (dezvăluite pompos mai sus) și fără cine știe ce pregătiri — cam ca în acest exemplu cu vreo 5 comenzi directe (în consola R standard, chiar fără tidyverse):

# Inițializează o "fereastră grafică" și parametrii a, b
plot(0, type="n", xlim = c(-1.5, 1.5), ylim = c(-1, 1))
a <- 0.8; b <- 0.48  # ... mai mici ca 1 (!)
# Constituie o rețea de puncte (x, y), de exemplu cu pasul (orizontal, vertical) 0.01
X <- seq(-1.5, 1.5, by = 0.01)  # vreo 300 de abscise, din sutime în sutime
Y <- seq(-1, 1, by = 0.01)  # vreo 200 de ordonate
# Calculează F(x,y) pe fiecare punct (x,y) al rețelei
Z <- outer(X, Y, function(x,y) {
                 a^4-b^4-2*a^2*x^2+x^4+2*a^2*y^2+2*x^2*y^2+y^4}
     )  # Z = F(x,y)
# Trasează curbele de ecuații Z = F(x,y) ∈ {0.2, 0.4, 0.6,..., 2}
contour(X, Y, Z, levels = seq(2, 20, by=2) / 10)

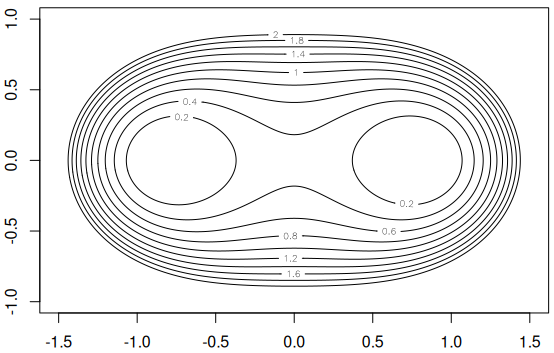
Indicațiile strecurate în comentariile inserate comenzilor ne par suficiente pentru a înțelege funcțiile R outer() și contour()… Subliniem doar că nivelarea valorilor $F(x,y)$ la altă valoare decât zero — prin $F(x,y)=\beta\ne 0$ — induce cumva o anumită modificare a parametrilor inițiali, încât rezultă contururile pentru o anumită familie de mai multe "ovale Cassini"; de fapt $Z=F(x,y)=\beta$ reprezintă secțiuni plane (la cotele $\beta$ ale axei $Oz$) ale unui anumit corp (un tor) reprezentat în sistemul de coordonate $Oxyz$ al spațiului obișnuit — analog cazului știut probabil de prin liceu: conicele sunt secțiuni plane ale unui con.

Dar cele vreo 5 comenzi redate mai sus nu ajung, dacă vrem să evidențiem grafic, într-un caz sau altul, "alura și punctele importante ale adevăratei curbe"; așa că trebuie totuși, să ne facem timp pentru… "marafeturi" (iar revizuind când și când, cele de mai sus, constatăm că până să ne ocupăm de programe, se cuvine să facem unele completări).

Între timp… (completări)

Este clar că mai sus, am cam expediat "tipicul obișnuit manualului de liceu"… Dar cam pe nedrept: în cazul nostru este ușor de stabilit intersecția cu axele, iar aceasta devine foarte importantă: ne arată deja, cam ce cazuri am avea de investigat și după o mică analiză suplimentară, ne arată cam ce formă are curba în fiecare caz.

Să desemnăm prin $\boldsymbol\Gamma$ curba cu ecuația $F(x,y)=0$. Avem:

Se vede mai întâi că intersecțiile lui $\boldsymbol\Gamma$ cu axele depind de cum este $a$ față de $b$ (de exemplu, dacă $a\lt b$ atunci două dintre cele 4 valori $x$ sunt imaginare).
E clar însă că, indiferent de caz, $\boldsymbol\Gamma$ taie axa $Ox$ în $x_1=\sqrt{a^2+b^2}$ (și simetric, $-x_1$); se pune problema dacă pe $\boldsymbol\Gamma$ există sau nu, puncte $(x,y)$ cu abscisa $x\gt x_1$ (chestiunea este tratată minuțios în [1], pe fiecare caz în parte — dar cazurile respective sunt specificate ca atare din start, nu "descoperite" pe parcurs).

Lemă. Dacă $x\gt \sqrt{a^2+b^2}$ atunci pentru orice $y\in\mathbb{R}$ avem $F(x,y)\boldsymbol{\gt} 0$.

Demonstrație. Regrupând termenii din definiția (1) a lui $F(x,y)$ — și apoi ținând seama că pătratele sunt pozitive — avem, pentru orice numere reale $x, y$:

Dacă $x\gt \sqrt{a^2+b^2}$, atunci $(x^2-a^2)^2 - b^4 \boldsymbol\gt 0$ — deci $F(x,y) \gt 0\quad$ q.e.d.

Rezultă că $\boldsymbol{\Gamma}=\{(x,y)\in\mathbb{R}^2\,|\,F(x,y)\boldsymbol{=}0\}$ este conținută între dreptele verticate $x=\pm \sqrt{a^2+b^2}$ (indiferent de cazurile $a, b$ care s-ar considera).

În ceea ce privește intersecțiile cu $Oy$, din (7) se vede că acestea sunt reale numai dacă $a \le b$ și avem două cazuri: dacă $a=b$ atunci $\boldsymbol{\Gamma}$ trece prin originea $O(0,0)$ (poate… de mai multe ori) și nu mai taie altundeva, axa $Oy$; dacă $a\boldsymbol{\lt}b$, atunci $\boldsymbol{\Gamma}$ taie $Oy$ în $y_1=\sqrt{b^2-a^2}$ (și simetric, în $-y1$).
Apare iarăși, problema de a lămuri dacă $\boldsymbol{\Gamma}$ trece prin puncte aflate deasupra nivelului $y=y_1$ (în cazul când $a\lt b$)…

Dar $f(x)$ este funcție continuă și derivabilă (cum ne-a asigurat "teorema de existență a funcțiilor implicite"), deci punctele "cel mai înalte" ale lui $\boldsymbol\Gamma$ corespund unora dintre rădăcinile derivatei. Din (4) avem $f'(x)=0\,\iff\, x\in\{0, \pm\sqrt{a^2-y^2}\}$.
Rezultă că (dar să nu uităm că suntem în cazul $a\lt b$) există două "cel mai înalte" puncte și acestea sunt punctele lui $\boldsymbol{\Gamma}$ pentru care $x=\pm\sqrt{a^2-y^2}$ — adică sunt intersecțiile dintre $\boldsymbol{\Gamma}$ și cercul $(\boldsymbol{\gamma}): \,x^2+y^2=a^2$ (de observat că intersecțiile sunt reale numai dacă ordonata comună a lor satisface condiția $y^2\le a^2$).

Să rezolvăm sistemul celor două ecuații folosind SageMath:

sage:: solve([F == 0, x^2 + y^2 == b^2], [x,y])
[[x == -1/2*sqrt(4*a^4 - b^4)/a, y == -1/2*b^2/a],
 [x == -1/2*sqrt(4*a^4 - b^4)/a, y == 1/2*b^2/a],
 [x == 1/2*sqrt(4*a^4 - b^4)/a, y == -1/2*b^2/a],
 [x == 1/2*sqrt(4*a^4 - b^4)/a, y == 1/2*b^2/a]]

Deci (chipurile, dacă $a\lt b$) cel mai înalte puncte ale lui $\boldsymbol\Gamma$ sunt:

Pentru $a=b$ am văzut mai sus că $\boldsymbol\Gamma$ taie $Oy$ numai în origine și fiindcă (8) rămâne valabilă, rezultă că dacă $a=b$ atunci $\boldsymbol\Gamma$ este formată din două "bucle" simetrice față de $Oy$, conținând fiecare punctul $O(0,0)$ și cuprinse împreună (și tangente laturilor) în dreptunghiul $[-b\sqrt{2},\,b\sqrt{2}]\times[-b/2,\, b/2]$ (mai putem observa că "buclele" respective trebuie să fie "simple", fără imbricări — fiindcă $\boldsymbol\Gamma$ este o curbă "de gradul 4", deci nu poate avea mai mult de 4 puncte coliniare).

Să observăm acum, mai precis poate, că (8) rămâne valabilă (în sensul că punctele respective sunt reale și nu imaginare) numai dacă $4a^4-b^4\,\ge\,0$, adică numai dacă $a\sqrt{2}\,\ge\,b$; deci cazul este nu $a\lt b$, ci mai tare: $\boldsymbol{a\lt b \le a\sqrt{2}}$.
Aceasta înseamnă, contrar, că dacă $b\,\boldsymbol{\gt}\,a\sqrt{2}$, atunci pe $\boldsymbol\Gamma$ avem un singur "cel mai înalt" punct, anume $(0,\,\sqrt{b^2-a^2})$; rezultă că în acest caz, $\boldsymbol\Gamma$ are forma unui oval (convex) care este cuprins (și este tangent laturilor) în dreptunghiul de colțuri opuse $\left(-\sqrt{a^2+b^2},\,-\sqrt{b^2-a^2}\right)$ și $\left(\sqrt{a^2+b^2},\,\sqrt{b^2-a^2}\right)$.

Ne-am cam întins cu această "mică" analiză ("completare" incompletă)… Reținem că avem de ținut seama de poziția lui $b$ nu numai față de $a$, dar și față de $a\sqrt{2}$.
Dar trebuie să precizăm că în [1] este considerată și poziția față de 1 (de exemplu, cazul specificat din start "$\,\boldsymbol{1\le c}\lt a \lt c\sqrt{2}\,$"); ne scapă deocamdată, motivul… (totuși nu credem că ar exista vreunul, pentru care parametrii n-ar putea fi subunitari).
Se prea poate să fi greșit pe undeva mai sus (de parcă încă n-am pățit destul ca "să mă învăț minte"), dar de-acuma… lăsăm calculatorului să ne dumirească !