Reluăm de unde oprisem în [3] (unde am redat și formulele de bază).

Instruirea calculatorului…

Am păstrat acest titlu din [3] (unde a început povestea), dar scopul nu este "instruirea calculatorului", cât propria instruire: cum am formula un program (în ce limbaj? R și… română) care să traseze, cu linii și punctele semnificative, curbe dintr-o anumită familie definită de o "funcție implicită" (oarecare, sau doar familia $\Gamma$)?

Trebuie niște clame, ca să îmbini o limbă (de ce engleză, if I love Romanian ?), niște limbaje, un "program" și… alte cele (dar nu-i cazul de telefon modern).
Și nu se poate spune că avem noroc: programatorii pretind ceva engleză, nu altceva; de la a V-a și până la BAC se învață microsoftWord, pseudocod și "siplasplas" (nu R și alte cele); și toată lumea dă din mouse și din deget pe un display sau altul, "ne auzim la telefon" și "ne vedem pe facebook"; iar de învățat să citim și să scriem am învățat în clasa I-a, nu mai este nevoie.

Un program nu se face "din mouse" și "a formula un program" este cât o poveste; pe cât se poate, avem de asigurat că lecturând programul (și povestea din jur) "chiar înțelegi cum se petrec lucrurile"; iar "povestea"… este de natură neprofesionistă, nu prea se poate reduce la comentarii strecurate zgârcit și în grabă, pe liniile programului (mai ales că de R… parcă n-a auzit nimeni pe aici; dar v. https://www.r-project.org/).

Constituim întâi un fișier-text "2512_1.R" (l-am denumit după an și lună) în care vom înscrie pe rând, funcțiile care exprimă în R formulele de calcul sintetizate în [3] (și unele care ajută exprimării acestora, sau servesc exprimării grafice ulterioare); ca și în alte limbaje, construcțiile se bazează pe funcții, proprii sau moștenite.

O funcție este introdusă prin "cuvântul-cheie" function(), modelează anumite calcule pe baza parametrilor explicitați în paranteză — putând însă folosi când va fi apelată și valori (inclusiv alte funcții) existente la un moment dat în afara definiției — și returnează rezultatul (de obicei, ultima valoare pe care a calculat-o).

# Funcția implicită F(x,y), cu un anumit domeniu și codomeniu
def_ovals <- function(x, y) {  # "ovale Cassini", notate Γ; v. [3]
    # ((x-a)^2 + y^2)*((x+a)^2 + y^2) - b^4  # cu focarele +/-(a, 0)
    a^4 - b^4 - 2*a^2*x^2 + x^4 + 2*a^2*y^2 + 2*x^2*y^2 + y^4  # F(x,y)
}

Am inventat numele "def_oval" și în loc de $F(3, 7.25)$ de exemplu, avem acum def_oval(3, 7.25); corpul funcției este încadrat de acolade, separând astfel o definiție de alta (însă dacă în corp avem o singură linie, atunci acoladele pot lipsi). În def_oval() avem două linii, dar prima este marcată la început cu '#', adică este o linie-comentariu, doar cu rol informativ (pentru cel care citește, nu pentru calculator). Definiția acestei funcții se bazează pe funcțiile (sau operațiile) predefinite care asigură calculul numeric obișnuit; este de subliniat că nu poate fi vorba de calcul exact — în mod inerent apar "erori de aproximare", dar în general acestea sunt (sau se vor a fi) "neglijabile".

Dar calculul indicat în corpul funcției redate mai sus nu va putea fi efectuat, decât dacă în momentul respectiv există undeva (în exteriorul funcției) variabilele $a$ și $b$, ale căror valori "intră" tacit în calculul realizat în interiorul funcției.
Convenim ca în toate funcțiile pe care le vom înregistra în "2512_1.R", să mizăm pe grija utilizatorului ca înainte de a le invoca, să specifice valorile cuvenite pentru $a$ și $b$.

Iată o mostră de utilizare (intenționat banală, adică tipică) a funcției, dar redată "neprofesionist" (cu prea multe comentarii "inutile"; de!... poveștile ca poveștile: se adresează tuturor, dar depinde de cum le spui ca să vezi cui se adresează):

vb@Home:~/25dec$ R -q  # lansează consola de comenzi R
> source("2512_1.R")  # încarcă fișierul de funcții
> a <- 1.5; b <- 2  # prin ';' putem înlănțui instrucțiunile pe o aceeași linie
> def_oval(3, 7.5)  # invocă "în orb" funcția, greșind însă numele acesteia
Error in def_oval(3, 7.5) : could not find function "def_oval"
> def_ovals(3, 7.5)  # având a și b (din exterior), se poate calcula F(x,y) 
[1] 4459.25  # rezultatul returnat de apelul funcției
>  # prompt-ul liniei pe care se așteaptă o nouă comandă

Să modelăm acum intersecția cu axele de coordonate (a curbei pe care am definit-o prin def_ovals()). Din [3] știm ca oricare curbă $\boldsymbol{\Gamma}$ taie $Ox$ la $\pm\sqrt{a^2+b^2}$, iar acelea pentru care $a\gt b$, taie $Ox$ și la $\pm\sqrt{a^2-b^2}$. $Oy$ este interceptat numai dacă $a\le b$, la ordonatele $\pm\sqrt{b^2-a^2}$. Este suficient să se returneze numai valorile strict pozitive (fiindcă expresia $F(x,y)$ conține doar pătrate de termeni):

cutOx <- function() { # intersecții cu Ox > 0
    Ox <- sqrt(a^2 + b^2)
    if(a > b) Ox <- c(Ox, sqrt(a^2 - b^2)) 
    Ox
}
cutOy <- function() { # intersecții cu Oy > 0
    if(a > b) return(NULL)
    sqrt(b^2 - a^2)
}

În R întâlnim câteva funcții denumite (contrar obiceiului) printr-o singură literă; c() (folosită mai sus în definiția funcției cut_Ox()) combină într-un vector valorile individuale indicate în paranteză. Dar ar fi momentul să spunem că putem obține informații despre o funcție (și exemple de folosire) tastând la prompt-ul consolei help(nume_funcție); de exemplu, help(c), sau help(return), help(if), etc.

Simetrizând față de originea axelor rezultatele furnizate de cutOx() și cutOy(), vom găsi limitele între care se întinde pe orizontală și pe verticală, graficul $\boldsymbol\Gamma$; divizând dreptunghiul rezultat, în "pătrățele" punctiforme suficient de multe, vom putea trasa (aproximativ) graficul curbei respective: calculăm valorile $F(x,y)$ (invocând def_ovals(x,y)) în "punctele" rezultate (e drept că sunt "pătrățele", nu chiar puncte, dar dacă sunt suficient de mici mai putem neglija diferențele); apoi n-avem decât să plotăm punctele de abscisă x și ordonată $F(x,y)$, obținând graficul curbei (cu aproximație imperceptibilă, față de graficul abstract).
Această idee n-ar trebui să pară "nouă": calculul aproximativ al $\int_a^b f(x)\,dx$ (întâlnit în liceu) se bazează pe o idee asemănătoare.

Pentru a constitui o asemenea rețea de "pătrățele", presupunem firește că pe $Ox$ și $Oy$ avem o aceeași unitate de măsură și vom folosi aceste două funcții:

div_x <- function(n) { # divide domeniul (Ox) în n puncte echidistante
    ix <- cutOx()
    if(length(ix) == 1)
        return(seq(-ix, ix, length = n))  # v. help(seq)
    return(c(seq(-ix[1], -ix[2], length = n/2),
           c(seq(ix[2], ix[1], length = n/2))))
}
div_y <- function(n) { # divide codomeniul (Oy) în n puncte echidistante
    iy <- if(b > a*sqrt(2)) sqrt(b^2 - a^2) else b^2 / (2*a)
    seq(-iy, iy, length = n)
}

De observat că în div_y() n-am mai invocat cut_Oy(), ci am inclus direct "corpul" acesteia, ținând seama însă (pe ramura else) de cazurile stabilite anterior în [3].

Mai departe, în funcția următoare constituim o rețea X×Y cu vreo mie (sau mai multe mii sau zeci de mii) de puncte ("pătrățele"); prin outer(), determinăm valorile $F(x,y)$ ale punctelor rețelei și apoi, prin contour() trasăm graficul pentru $F(x,y)\boldsymbol{= 0}$ (după ce, mai întâi, inițializăm o fereastră grafică "vidă", prin plot(); vezi neapărat, help(plot)):

# Conturează nivelul 0 al valorilor F(x,y), cu (x,y) din rețeaua X×Y
plot_ovals <- function(np = 1000, ...) {
  X <- div_x(np)
  Y <- div_y(np)
  q <- 1.25  # mărim puțin, dreptunghiul în care va apărea Γ 
  plot(0, type="n", asp=1, bty="n", xlab="", ylab="", xaxt="n", yaxt="n",
       xlim = q*range(X), ylim = q*range(Y))
  Z <- outer(X, Y, def_ovals)  # Z = F(x,y)
  contour(X, Y, Z, levels = 0,  # graficul curbei Z = 0 (F(x,y)=0)
          drawlabels = FALSE, add = TRUE, ...)
}

Precizăm că range() furnizează valorile minimă și maximă, din vectorul indicat.

Este de sesizat argumentul "...", care apare la plot_ovals() și apoi, în apelul contour(). "..." este un cuvânt-cheie, rezervat pentru a transmite prin apelarea primei funcții, anumite valori parametrilor cunoscuți de a doua funcție, apelată din interiorul primeia (vezi help("..."), de data aceasta între ghilimele, ca simbol rezervat).
contour() trasează efectiv graficul, dar trasarea depinde firește de anumiți parametri: cu ce grosime se desenează, linie plină sau întreruptă, ce culoare, etc.; funcția plot_ovals() va putea fi apelată prevăzând în locul "..." valorile dorite pentru parametrii de trasare, iar acestea vor fi preluate de contour() (în locul celor pe care altfel, le-ar folosi de obicei). De exemplu, apelul plot_ovals(lwd = 2) va transmite "lwd" (parametru neinvocat vreundeva, în corpul său) în argumentul "..." al funcției contour(), iar aceasta va trasa graficul aplicând grosimea 2 în loc de cea folosită implicit.

Am preferat să vizăm direct familia $\boldsymbol\Gamma$ — dar puteam imagina o funcție mai generală, plot_Fxy(FUN, np=1000, ...), unde "FUN" ar viza o funcție $F(x,y)$ oarecare (apelată în outer(X.Y, FUN)); atunci, graficul pentru $\boldsymbol\Gamma$ ar fi produs prin apelul plot_Fxy(def_ovals). Pentru graficul unei elipse de exemplu, ar trebui să definim o funcție "def_ellipse()", dar ar trebui și să redefinim funcțiile div_x() și div_y(); atunci plot_Fxy(def_ellipse) va desena elipsa respectivă. Putem evita redefinirile, prevăzând prototipul mai complicat plot_Fxy(FUN, Dx, Dy, np=1000, ...), în care Dx și Dy ar viza funcțiile de divizare specifice "FUN"; pentru $\boldsymbol\Gamma$ am apela atunci, plot_Fxy(def_ovals, div_x, div_y, ...).

Este adevărat că vor fi de evidențiat anumite cercuri și elipse, asociate cu $\boldsymbol\Gamma$; dar acestea se pot trasa mai simplu, fără a folosi contour() (de exemplu, cercul de centru $z_0\in\mathbb{C}$ și rază $r$ are ecuația parametrică $z=z_0 + re^{i\phi}$ și poate fi trasat plotând punctele $z$ corespunzătoare unei divizări suficient de fine, $\phi\in[0,2\pi]$):

# Puncte pe Elipsa (Cerc) de centru și semiaxe (rază) date
ellipse <- function(z0, a, b = a) {
    tau <- seq(0, 2*pi, length = 600)
    z0 + a*cos(tau) + 1i*b*sin(tau)
}

Pentru a trasa tangente și pentru a determina inflexiunile de formă (convexă / concavă), avem nevoie de derivate (am redat în [3], formulele de bază):

# Tabloul derivatelor parțiale. Prima și a doua derivată într-un punct (x,y)
partial_deriv <- function(x, y) {
    p <- x^2 + y^2 - a^2
    q <- x^2 + y^2 + a^2
    c(
        4*x*p,        # Fx (derivata în raport cu x)
        4*y*q,        # Fy
        4*p + 8*x^2,  # Fxx
        8*x*y,        # Fxy (= Fyx)
        4*q + 8*y^2   # Fyy
    )
}
f_prim <- function(x, y)  # (= -Fx/Fy)
    -x*(x^2 + y^2 - a^2) / (y*(x^2 + y^2 + a^2))
f_secd <- function(x, y) {  # v. (de exemplu) [3]
    D <- partial_deriv(x, y)
    (-D[2]^2*D[3] + 2*D[1]*D[2]*D[4] - D[1]^2*D[5]) / D[2]^3
}

Să observăm însă că f_prim(x0, y0) ne permite să calculăm panta tangentei în punctul de abscisă dată, $\boldsymbol{f'}(x0)$, numai dacă știm și valoarea y0 corespunzătoare pe curbă abscisei respective… Deci, până la urmă, tot ar fi nevoie să explicităm $y = f(x)$, din $F(x,y)=0$ (ceea ce am evitat de la bun început, mizând pe faptul că prin contour() putem produce direct graficul, fără a explicita).
Dar nici n-ar fi greu de explicitat: $F(x,y)=0 \iff (x^2+y^2+a^2)^2=4a^2x^2+b^4$, de unde, aplicând radicalul, avem imediat:

Grație simetriilor, putem considera numai punctele din primul cadran:

# Ordonata pozitivă a punctului (x0, y) ∈ Γ, x0 > 0
y_at_x <- function(x0) 
    sqrt(sqrt(b^4 + 4*a^2*x0^2) - a^2 - x0^2)
# Capetele unei bucăți din tangenta într-un punct din primul cadran, 
# de abscisă dată; punctul de contact este mijlocul segmentului 
tangent <- function(x0) {
    y0 <- y_at_x(x0) 
    m <- f_prim(x0, y0)
    c(x0-0.6, y0 - m*0.6, x0+0.6, y0 + m*0.6)
}

Subliniem că tangent() returnează doar capetele unei bucăți de tangentă (de lungime rezonabilă) centrată în punctul de tangență; "tangenta" respectivă va fi adăugată pe graficul curbei prin apelarea funcției segments() (transmițându-i capetele respective).

Putem zice că am terminat (și povestea ?): folosind funcțiile înscrise până acum în fișierul "2112_1.R", putem reprezenta grafic $\boldsymbol\Gamma$ și putem experimenta pentru diverse valori ale parametrilor $a$ și $b$ (vizând totuși cazurile depistate în [3]).

Apelând points(), sau lines(), vom putea adăuga pe grafic diverse puncte și linii importante, evidențiindu-le eventual prin grosime, formă și culoare. Ar fi necesar să și etichetăm, anumite puncte sau linii? Poate că da, în anumite contexte în care sunt referite elemente ale figurii (având atunci grija de a nu "încărca" excesiv, desenul respectiv); putem folosi pentru aceasta, funcțiile labels() și text() — dar va trebui să procedăm "de la caz la caz", fiindcă poziția etichetei (deasupra punctului, la dreapta lui, etc.) depinde totuși de graficul curent (și firește, trebuie evitate suprapunerile).
Desigur, figura rezultată "pe calculator" se adresează celui care știe să (o) citească… (și tocmai de aceea, se cuvine să nu încărcăm figura cu elemente și notații inutile)

Un experiment cu panouri

Mai întâi, în scopuri didactice, s-ar cuveni să arătăm împreună, cazurile posibile de ovale $\boldsymbol\Gamma$ — marcând doar focarele $F_1$, $F_2$ și evidențiind proprietatea $PF_1\times PF_2=b^2$.

Constituim un nou fișier "2512a.R", în care după ce importăm (prin source()) funcțiile constituite mai sus, constituim o fereastră cu 4 panouri (folosind mfrow din par()), definim o funcție care să adauge o "legendă" explicativă panoului pentru care va fi apelată, apoi iterăm (prin for()) pe un set de 4 cupluri $a$ și $b$ (câte unul pe panou), invocând pentru fiecare caz plot_ovals(), marcând un punct $P$ al curbei (cu ordonata dată de y_at_x()), focarele ovalului curent, segmentele $PF_1$ și $PF_2$ și adăugând apoi (prin set_legend()) legenda asociată panoului curent:

source("2512_1.R")
# Împarte fereastra grafică în 4 panouri
opar <- par(mfrow = c(2, 2), mar = rep(0.1, 4), 
            xaxt="n", yaxt="n", bty="n")
# Vom atașa o "legendă", fiecărui panou
LGD <- c("b < a", "b = a", 
         expression(paste("a < b < a", sqrt(2))),
         expression(paste("a", sqrt(2), "<= b"))
)
set_legend <- function(idx) {
    legend("bottom", legend = LGD[idx], 
           bty="n", text.font=2, cex=1.2)
} 
# vectori cu valori pentru a și respectiv b (o pereche de fiecare panou)
A <- c(1.2, 2, 2, 2) 
B <- c(1.16, 2, 2.025, 3.2)
# Plotează în fiecare panou, evidențiind focarele și legătura punctelor
for(i in 1:4) {
    a <- A[i]; b <- B[i]
    plot_ovals(lwd = 1.1)
    x0 <- a/2
    y0 <- y_at_x(x0)  # un punct P(x0,y0) al curbei
    points(c(-a, a, x0), c(0, 0, y0), cex=0.4)
    lines(c(-a,x0, a), c(0,y0,0), lwd=0.6)
    text(c(-a, a, x0), c(0, 0, y0), pos=c(1, 1, 3),
         labels=c(expression(F[2]), expression(F[1], "P")))
    set_legend(i)
}
# Adaugă deasupra panourilor, un "titlu"
legend(x=-9, y=14, legend=expression(paste(
    "Ovale Cassini: ", PF[1] %*% PF[2], " = ", b^2)), 
    bty="n", text.font=4, cex=1.3, xpd="NA")
par(opar)  # reconstituie parametrii grafici inițiali

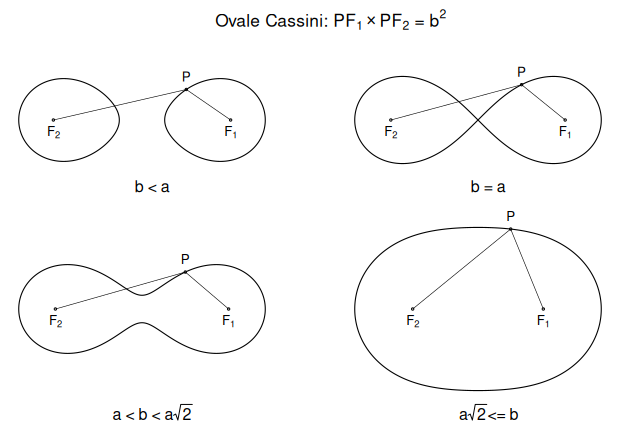
În final, am apelat legend(), evitând însă parametrul xpd (setându-l pe "NA"), pentru a înscrie undeva deasupra panourilor, un "titlu" (în care am uitat să mai fi consemnat și că $F_1F_2=2a$…). Dar n-am uitat la sfârșit, să reconstituim (prin par()) parametrii grafici inițiali, salvați la debutul programului în variabila "opar".

Ce poate spune figura…

Acum să exploatăm programul din "2512_1.R" pentru o figură "completă", să zicem pe cazul (cel mai interesant) $\boldsymbol{a\lt b \lt a\sqrt{2}}$. Observând, marcând puncte, "măsurând" sau calculând segmente și unghiuri — putem "descoperi" diverse proprietăți ale curbelor $\boldsymbol\Gamma$ (că și de asta, te apuci să faci o figură…); pe de altă parte, completând progresiv figura, putem constata dacă nu cumva încă lipsește, sau trebuie modificat ceva, în programul de care mai sus ziceam că "am terminat" (de obicei… nu termini).

Constituim deci un nou fișier "2512b.R" (alt fișier… altă poveste):

##   a < b < a*sqrt(2)   ##
source("2512_1.R")
a <- 1.05; b <- 1.1
plot_ovals(lwd = 1.1)

# Marchează focarele F1 și F2
points(c(-a,a), c(0,0), cex=0.4)
text(c(-a,a), c(0,0), labels = c(expression(F[2]), expression(F[1])), 
     pos = 1, font = 2, family="sans")

# Trasează axele, marchează intersecții și tangente în primul cadran
x1 <- sqrt(a^2 + b^2)
y1 <- sqrt(b^2 - a^2)
points(c(x1, 0, 0), c(0, y1, 0), cex=0.4)  # punctele A, B și O(0,0)
segments(x0 = c(-0.3, x1), y0 = c(y1, -0.3),  # tangente în A, B
         x1 = c(0.3, x1), y1 = c(y1, 0.3), lwd = 0.6)
text(c(x1-0.02,0, 0), c(0,y1, 0), labels = c("A", "B", "O"), 
       pos = c(4, 1, 1), offset=0.3, family="sans")
arrows(x0 = c(-x1-0.2, 0), y0 = c(0, -y1-0.5),  # axele ovalului
       x1 = c(x1+0.25, 0), y1 = c(0, y1+0.5),
       length=0.1, lwd=0.25, col="gray10")

# Cel mai înalte puncte și bitangenta (v. [3])
xm <- sqrt(4*a^4 - b^4) / (2*a)
ym <- b^2 / (2*a)
points(c(xm, -xm), c(ym, ym), cex=0.4)
lines(x = c(-xm-0.3, xm+0.3), y = c(ym, ym), lwd=0.6)
text(xm, ym, labels="M", pos=3, offset=0.3)  # un punct maxim, M
segments(0,0, xm, ym, lty=2, lwd=0.6)  # segmentul OM...

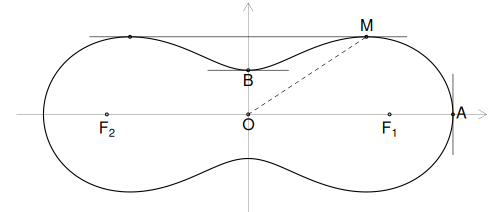
Punctele maxime (adică $M$, simetricul său față de axa orizontală și simetricele acestora față de verticală) formează un dreptunghi centrat în $O$, deci sunt (banal) conciclice; cercul respectiv fiind evident, nu are rost să-l trasăm !
Însă, observând raza $MO$… parcă avem $MO=OF$ — ceea ce se confirmă ușor: $MO=\sqrt{(xm)^2+(ym)^2}=a=OF$. Cercul punctelor maxime trece deci prin focare, ceea ce nu mai este banal (și rămâne de verificat pentru celelalte cazuri de ovale) — așa că se cuvine să figurăm acest cerc (îl vom nota cu $\boldsymbol\gamma$).

"Ștergem" segmentul $OM$ (devenit inutil în urma constatării făcute mai sus) și trasăm în loc, cercul $\boldsymbol\gamma$ (cu ellipse(), din "2512_1.R"):

# Cercul punctelor "maxime" trece prin focare
points(ellipse(0+0*i,a), type="l", lty=2, lwd=0.6)
text(a/2+0.1, -2*a/3-0.25, labels = expression(paste(gamma)))

Pe noua imagine (pe care n-o mai prezentăm aici) sare în ochi faptul că $MF_1 \boldsymbol{\perp} MF_2$, dar justificarea este imediată: unghiul $F_1MF_2$ este înscris într-un semicerc (și fiind "imediată", nu-i cazul să și trasăm segmentele respective — am încărca inutil figura).

Obs. Cercul $\boldsymbol\gamma$, cu diametrul $F_1F_2$ nu depinde de $b$ (ci numai de $a$); prin urmare, punctele "maxime" ale tuturor curbelor $\boldsymbol\Gamma$ care au aceleași focare, $F_1$ și $F_2$, sunt situate pe cercul de diametru $F_1F_2$ (proprietate care nu "sare în ochi" pe figură!).

În [1] se justifică, folosind inegalități într-adevăr elementare, că $F(x,y$) crește în stânga lui $M$ (pentru punctele de pe arcul $BM$) și descrește în dreapta. De fapt, nu se poate altfel: dacă între $B$ și $M$ (care corespund unui minim și maxim local) $F(x,y)$ n-ar fi crescătoare, atunci (ținând cont și de simetria față de $Oy$) ar însemna că există o dreaptă care să taie $\Gamma$ în mai mult de 4 puncte, ceea ce este imposibil (având un sistem format dintr-o ecuație de grad 4 și una de grad 1).

Graficul este convex în jurul lui $B$ și este concav în jurul lui $M$; deci pe parcursul strict crescător de la $B$ la $M$ există neapărat un punct de inflexiune și se cuvine să-l marcăm. Am avea de rezolvat ecuația $f''(x,y)=0$, implicând funcțiile def_ovals(), f_secd() și y_at_x() din programul nostru; am încercat (fără a particulariza $a$ și $b$) să determinăm $(x,y)$ pentru care f_secd(x,y)=0, folosind desigur SageMath — dar rezultatul furnizat (dacă se mai ajunge la el) acoperă aproape o coală întreagă…

"Salvarea" a venit citind mai atent [1] (partea a II-a), unde se observă că în $F_{xx}$ — "care este un factor al unui termen al numărătorului" fracției care dă $f''(x,y)$ — intră expresia $3x^2+y^2-a^2$, "și deci este interesant să considerăm și elipsa" $(\boldsymbol{\varepsilon})$ de ecuație $\boldsymbol{3x^2+y^2-a^2=0}$; apoi, se determină intersecțiile elipsei $\boldsymbol{\varepsilon}$ cu $\boldsymbol{\Gamma}$ și se analizează semnul lui $f''$ în punctele elipsei; constatarea că $f''$ schimbă de semn după cum $(x,y)$ este interior sau exterior elipsei, conduce la concluzia că intersecțiile găsite sunt chiar punctele de inflexiune ale lui $\boldsymbol{\Gamma}$ (un raționament chiar superb și care ne poate scuti de calcule complicate)

Bineînțeles că am apelat iarăși la SageMath (de!… nu-i ușor să te înveți minte), ca să obțin intersecțiile respective — dar nici de această dată, n-am putut rezolva eroarea "The catch MACSYMA-QUIT is undefined while evaluating load(to_poly_solve)" (și nici alții n-au putut, de prin 2014 încoace; dacă foloseam valori numerice în loc de $a$ și $b$, probabil că se rezolva, dar nu asta ne interesa). SageMath implică foarte multe sisteme; de unele am mai auzit și chiar am folosit (SymPi, Pari, GMP), de altele aud prima dată ("MACSYMA"); devine clar că e pentru profesioniști, nu pentru "alde-mine"…
Uităm de-acum de SageMath; în treacăt fie spus, o ecuație cu coeficienți numerici putem rezolva comod și mulțumindu-ne cu R (v. funcția polyroot(), sau uniroot()).

Înlocuind $y^2$ cu $a^2 - 3x^2$ în $F(x,y)=0$ și lucrând cu atenția cuvenită, chiar nu-i greu să găsim manual că

Sunt valabile ambele soluții $x$ (fiindcă în cazul nostru $a\lt b\lt a\sqrt{2}$, avem $3a^2 \gt \sqrt{5a^4 + b^4}$); dar trebuie să fie pozitiv și $y^2=a^2-3x^2$, ceea ce constatăm că impune alegerea semnului "$-$" în fața radicalului de mai sus. În final, cele 4 intersecții reale dintre elipsa $\boldsymbol\varepsilon$ și $\boldsymbol\Gamma$ sunt: $$x_{1,2} = \pm \sqrt{3v - u},\,\,y_{1,2}=\pm\sqrt{3u - 7v}\quad \textrm{cu}\,\,\, u=\frac{\sqrt{5a^4+b^4}}{2},\,\,v=\frac{a^2}{2}$$

și acum putem continua programul:

# Punctele de inflexiune se află pe elipsa F_xx = 0
points(ellipse(0+0*i, a/sqrt(3), a), type="l", lty=2, lwd=0.6)
text(-a/sqrt(3)-0.05, -0.2, labels=expression(paste(epsilon)))
lines(x=c(-0.4,0.4), y=c(a, a)+0.0075, lwd=0.5)
points(0, a, cex=0.4)
text(0,a, labels="E", offset=0.3, pos=3)
# Calculează și marchează punctele de inflexiune
u <- sqrt(5*a^4 + b^4) / 2
v <- a^2 / 2
p <- sqrt(3*v - u)
q <- sqrt(3*u - 7*v)
X <- c(p, p, -p, -p)
Y <- c(q, -q, q, -q)
points(X, Y, cex=0.4)
#  Figurează tangenta într-un punct de inflexiune
m <- f_prim(p, -q)  # pentru cadranul IV
segments(p-0.3, -q - m*0.3, p+0.25, -q + m*0.25)

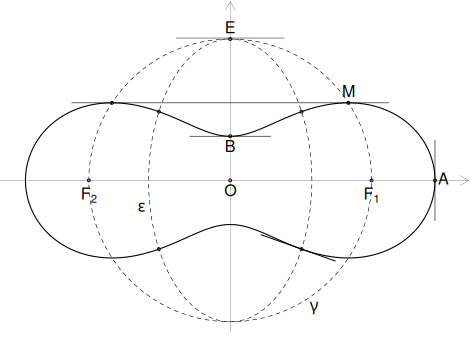
Față de figura anterioară, am mărit puțin axa verticală (ca să încapă cercul $\boldsymbol\gamma)$.
Elipsa $\boldsymbol\varepsilon$ are axele $a/\sqrt{3}$ (pe $Ox$) și $a$ (pe $Oy$, marcată $OE$), deci $OE=OF_1$ adică cercul $\boldsymbol\gamma$ și elipsa $\boldsymbol\varepsilon$ sunt tangente în $E$ (iar elipsa este conținută în interiorul cercului, fiindcă "axa mare" a ei este mai mică decât raza cercului).

În punctul de inflexiune din cadranul IV (intersecție a elipsei cu ovalul) am figurat o mică bucată a tangentei la oval… Surpriză desigur: figura spune că punctul respectiv NU este un punct de inflexiune (căci atunci, tangenta ar fi fost, în jurul acelui punct, de o parte și de cealaltă a curbei, ori vedem că ea este toată dedesubt).

Obs. Faptul că punctele respective sunt pe un același cerc cu centrul în $O$ (până a fi și pe elipsa indicată) decurge imediat din simetria față de axe; la fel, punctele de inflexiune sunt sigur, pe un cerc cu centrul $O$ ("surpriza" fiind că aceste două cercuri nu coincid…)

Am greșit undeva? Nu eu, calculatorul? Am repetat programul pentru alte valori $b$; iar cu $b=1.056$ rezultă o figură pe care se vede clar că tangenta respectivă este (într-adevăr…) dedesubtul curbei — încât ni se pare ieftin să dăm vina pe calculator (sau pe R; sigur ajungeam la aceeași figură și dacă foloseam nu R, ci de exemplu SageMath).

Nu-i posibil oare, ca în raționamentele și calculele care au legat elipsa $3x^2+y^2=a^2$ de punctele de inflexiune ale lui $\boldsymbol{\Gamma}$, să se fi strecurat totuși ceva greșit? Ar fi de observat, ca și mai sus în cazul cercului $\boldsymbol\gamma$, că această elipsă depinde numai de $a$ — deci ar rezulta că punctele de inflexiune ale tuturor ovalelor Cassini cu aceleași focare, ar fi situate pe elipsa $\boldsymbol\varepsilon$ (…vom arăta mai jos că nu este adevărat!)

E greu de reluat și de verificat totul, din nou (recitind și tot recitind), pentru a depista ceva greșit… Dar ar mai fi o idee, care probabil că ar evidenția dacă legarea de elipsa $\boldsymbol\varepsilon$ a punctelor de inflexiune este sau nu, corectă.

Revenire la calculul punctelor de inflexiune

Punctele de inflexiune se află printre rădăcinile ecuației $f''(x)=0$; cum am evocat mai sus, încercarea de a le determina în formă simbolică (literală) a eșuat.
Atunci… să lăsăm calculatorul să le găsească (în contextul concret curent) !

Ideea este foarte simplă: pentru valorile date $a$ și $b$, parcurgem cu un pas suficient de mic, abscisele $x$ ale punctelor de pe arcul $BM$, începând de la 0 spre abscisa punctului maxim $M$; prin y_at_x() aflăm ordonata $y$ a punctului de pe arc, corespunzător abscisei $x$. Apoi, putem invoca f_secd(x,y); la început, pentru o serie de abscise $x$ nu prea depărtate de 0, valorile rezultate $f''(x)$ (pentru punctul $(x,y)$ curent) vor fi pozitive (fiindcă în jurul lui $B$ graficul este convex); cu alte cuvinte, în primul moment în care, tot avansând $x$, s-ar găsi $f''(x)\boldsymbol{\le 0}$ — abscisa curentă respectivă aproximează (suficient de bine) punctul de inflexiune aflat în primul cadran.

Revenim în fișierul "2512_1.R" și adăugăm funcția:

# Punctul de inflexiune din primul cadran
inflex <- function() {
    for(xi in seq(0, sqrt(4*a^4 - b^4) / (2*a), 
                  length=10000)) {
        yi <- y_at_x(xi)
        if(f_secd(xi, yi) <= 0)
            return(c(xi, yi))
    }
}

Iar în "2512b.R" adăugăm:

# Marchează punctele de inflexiune și tangenta din cadranul I
flx <- inflex()
p <- flx[1]
q <- flx[2]
points(p, q, cex=0.4)
m <- f_prim(p, q)  # panta tangentei...
segments(p-0.25, q - m*0.25-0.03, p+0.25, 
         q + m*0.25+0.03, col="blue")

Se poate observa că de data aceasta, pentru trasarea segmentului de tangentă n-am respectat exact panta calculată, ci am rotit puțin tangenta (totuși imperceptibil) — pentru a o distinge mai bine față de graficul curbei (ceea ce se poate admite, ținând seama de natura didactică a studiului) și în același scop, am trasat-o cu "blue":

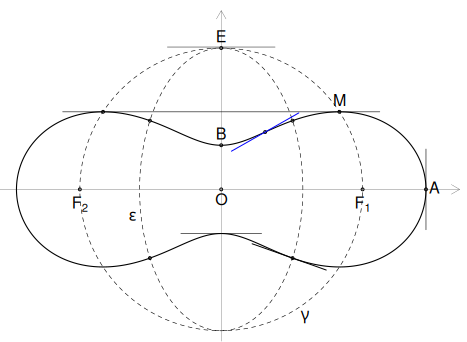
Pentru lizibilitate, n-am mai dus tangenta prin $B$ (ca în figura anterioară), ci prin opusul acestuia (uitând însă că acesta ar trebui marcat).

Calculul de mai sus (validat acum și de imagine) arată că elipsa $\boldsymbol\varepsilon$ nu are de-a face cu punctele de inflexiune; ca urmare, nevăzând și neștiind vreo legătură a ei cu $\boldsymbol\Gamma$, o vom șterge din figură (rămâne poate de studiat o asemenea legătură…).

Desigur, făcând aceste eliminări, figura "sărăcește"; putem însă îmbunătăți lucrurile, ținând seama de acest rezultat important, aflat din cărți vechi (dinainte de 1930) disponibile încă pe Internet (v. și courbes.2d): locul punctelor de inflexiune ale ovalelor Cassini cu aceleași focare este o lemniscată Bernoulli. Ecuația acesteia este (de observat că nu depinde de $b$, deci vizează toate ovalele homofocale):

și o trasăm imitând funcția plot_ovals():

# Puncte de inflexiune se află pe o lemniscată Bernoulli
V <- div_x(1000)
W <- 4*div_y(1000)
bern <- function(x, y)
    (x^2+y^2)^2 - a^2*(y^2-x^2)
Z <- outer(V, W, bern)  # Z = F(x,y)
contour(V, W, -Z, levels = 0, drawlabels = FALSE, add = TRUE, lty=2)

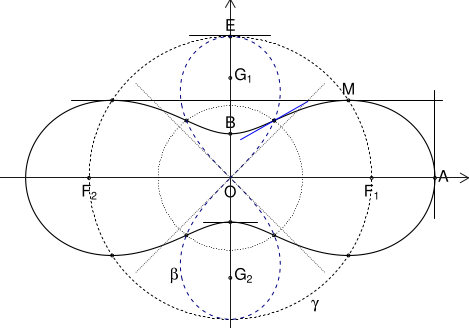
Figura e gata (nu mai redăm aici cum am marcat focarele $G_{1,2}$ ale lemniscatei $\boldsymbol\beta$, sau bisectoarele sistemului de axe, tangente în $O$ lemniscatei); se observă că am desenat (invocând ellipse(0,sqrt(p^2+q^2)) și specificând o trasare prin puncte) și cercul care trece prin punctele de inflexiune (deși nu era necesar, fiind evident că punctele respective sunt conciclice; de aceea, nici nu l-am etichetat).
Nu mai avem ce elimina. Poate… să exemplificăm două cercuri osculatoare, în $A$ și $B\,$?; doar că într-adevăr interesant, ar fi să trasăm alăturat curba osculatoare, definită de centrele cercurilor osculatoare în toate punctele lui $\boldsymbol{\Gamma}$… ceea ce ar fi altă poveste.

Dar să recapitulăm: în cazul $a\lt b \lt a\sqrt{2}$, curba $\boldsymbol\Gamma$ este cuprinsă (tangent) în dreptunghiul determinat de cele două bitangente ale sale și de tangentele în vârfurile de pe axa focarelor $F_{1,2}$; focarele și punctele "maxime" sunt situate pe cercul $\boldsymbol\gamma$; punctele de inflexiune sunt situate pe lemniscata Bernoulli $\boldsymbol\beta$, care este tangentă în $O$ bisectoarelor sistemului de axe (și tangentă în $E$ cercului $\boldsymbol\gamma$) și are linia focarelor $G_1G_2$ perpendiculară pe linia $F_1F_2$ a focarelor lui $\boldsymbol\Gamma$.
Și fiindcă ecuațiile lui $\boldsymbol\gamma$ și $\boldsymbol\beta$ implică numai $a$ (nu și $b$), toate curbele $\boldsymbol\Gamma$ care au aceleași focare (anume $\pm(\boldsymbol{a}, 0)$) și care satisfac condiției $a\lt b \lt a\sqrt{2}$, își au punctele "maxime" pe cercul $\boldsymbol\gamma$ și punctele de inflexiune pe lemniscata $\boldsymbol\beta$.