Urmând calea arătată în [2], prevedem fişierele declarative mnemonics.sty şi unics.fd astfel încât simbolurile definite într-un fişier monics.mf să poată fi utilizate ca atare în documente LaTeX:

%% mnemonics.sty
\DeclareSymbolFont {mnem} {U}{nics}{}{}
\DeclareMathSymbol \bernu {\mathord}{mnem}{"00}
\DeclareMathSymbol \bernurot {\mathord}{mnem}{"1E}
\DeclareMathSymbol \circo {\mathord}{mnem}{"10}
\DeclareMathSymbol \circorot {\mathord}{mnem}{"11}
\DeclareMathSymbol \circbern {\mathord}{mnem}{"08}
\endinput

%% unics.fd
\DeclareFontFamily{U}{mnemsym}{}
\DeclareFontShape{U}{nics}{}{}{<-> [3] monics}{}

Am declarat fontul denumit "mnem" (într-o familie "mnemsym"), conţinând cinci anumite simboluri matematice; caracteristicile metrice ale acestora se vor găsi în fişierul monics.tfm, iar formele grafice vor fi puse la dispoziţie în fişiere monics.*pk (denumirile pentru font şi familie sunt convenţionale; în [2] acestea coincid, ceea ce nu este necesar).

Dacă xelatex (ori pdflatex) va întâlni în preambulul fişierului pe care îl compilează comanda usepackage{mnemonics}, atunci va citi cele două fişiere de mai sus şi va încărca fişierele de metrică şi de grafică asociate [ iar dacă acestea nu există în momentul compilării, atunci va încerca să le creeze (v. [2]), invocând mf pe fişierul monics.mf şi programul mktexpk ].

Detaliem întâi (pe secţiuni) construcţia simbolurilor respective; apoi formulăm fişiere Latex în care folosim fontul creat. Avem astfel prilejul de a diseca şi lămuri aspecte specifice sistemului TeX şi limbajului MetaFont; programul mf este compilator (în sensul că produce fişiere binare, dintr-un text cu o sintaxă specifică), dar este şi interpretor - încât vom putea profita de mesajele informative furnizate în diverse contexte de lucru (la fel putem zice despre pdftex, xelatex, etc.).

Fişierul MetaFont monics.mf

monics.mf înglobează în mod tacit câteva secţiuni distincte: funcţii auxiliare; constante de bază; unităţi de măsură şi dimensionarea simbolurilor; alegerea peniţelor; definirea propriu-zisă a caracterelor respective (în această ordine).

Avem două funcţii (sau macro-uri) auxiliare; altele vor putea fi adăugate, dacă va fi cazul.
Funcţia rectangle() produce un contur dreptunghiular "paralel" cu axele de coordonate:

vardef rectangle(expr A, Z) =  % Dreptunghi de centru Z, cu laturile paralele axelor
    pair B, C, D;              % (v. [4]) 
    A + C = B + D = 2Z;  % Condiţia ca ABCD să fie paralelogram cu centrul Z
    xpart(D) = xpart(A);  % apoi, AD || Oy
    ypart(A+D) = ypart(B+C);  % iar dreapta prin mijloacele lui AD şi BC este || Ox
    A+3(-1,1) -- B+3(1,1) -- C+3(1,-1) -- D+3(-1,-1) --cycle
enddef;

Vom folosi acest macro pentru a trasa "cadrul tangent" lemniscatei lui Bernoulli; faţă de [4] am mărit uşor dreptunghiul, încât să aibă cât mai puţini pixeli comuni cu bitmap-ul corespunzător simbolului (de exemplu, A+3(-1,1) mută punctul iniţial A spre stânga şi în sus cu câte 3 pixeli; B+3(1,1) trage B spre dreapta şi în sus cu câte 3 pixeli. Teoretic, AB fiind tangentă lemniscatei, are un singur punct comun cu aceasta; dar practic, punctele "teoretice" sunt rotunjite la pixeli - ceva mai precis, la centrul câte unui pixel pătratic).

Funcţia arrowz() produce o mică săgeată, în punctul indicat (şi cu direcţia dată):

vardef arrowz(expr Z, fi) =  % săgeată ('>') în punctul Z, axată pe direcţia 'fi'
    (Z+8(-2, 1) -- Z -- Z+8(-2, -1)) rotatedaround(Z, fi)
enddef;

Z este deplasat spre stânga cu 16 pixeli şi în sus, respectiv în jos, cu câte 8 pixeli - rezultând o "săgeată orizontală" cu vârful în Z (ca ">"), al cărei unghi interior este de 2*arctg(1/2) ≈ 54°; apoi, aceasta este rotită în jurul lui Z cu unghiul indicat. Vom folosi acest macro pentru a marca vectorul de poziţie al centrului cercului care trece prin origine (dacă săgeata se va dovedi a fi prea boantă, atunci am putea înlocui factorul 8 cu unul mai mare).

Raza cercului determină distanţa dintre focarele lemniscatei (şi implicit, orice altă distanţă ar fi de considerat; v. [3]). Alegem R = 1, considerând că altfel, fie lăţimile, fie înălţimile celor două carac­tere (cercul şi lemniscata) ar fi într-un raport mai puţin convenabil:

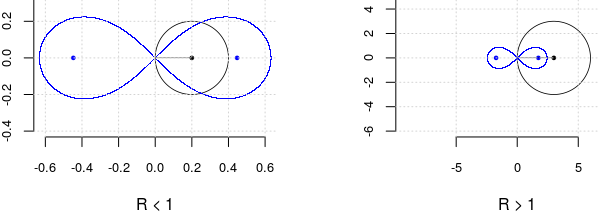
R = 1;  % raza cercului (constanta de bază); 
          % R = .2 (R < 1 => F > R; micşorând R, creşte disproporţia orizontală)
          % R = 3 (R > 1 => F < R; mărind R, creşte disproporţia verticală)
F = sqrt R;  % semidistanţa focală
sax = F*sqrt(2);  % semiaxa lemniscatei
xhi = F*sqrt(3)/2;  % distanţa la Oy a punctelor cel mai înalte (pe lemniscată)

Ca să fie realmente "distanţe", aceste valori numerice trebuie scalate cumva, după capabilităţile dispozitivului concret de ieşire (ecranul sau imprimanta care va reda acele caractere). Folosim modul de ieşire 'ljfour' (v. [3]), pentru imprimante LaserJet 4 (cu rezoluţia 600dpi) şi alegem ca unitate de măsură u# := 20pt#; deci R=1 ar măsura 20*600/72.27 ≈ 166 pixeli (cam 0.7cm, fiindcă avem 600 pixels_per_inch, iar 1in (=72.27pt) = 2.54cm):

mode := ljfour;  % 600 dpi ("dots per inch", sau "pixels_per_inch")
%% font_size 12pt#;  % "design size", cu valoarea implicită 128pt
mode_setup;
u# := 20pt#;  % (≈0.7cm) Aici putem regla (odată fixat R) mărimea simbolurilor
define_pixels(u);  % pixeli pe unitatea (abstractă) de măsură: 166

'ljfour' este folosit în mod implicit de către xelatex şi pdflatex, când este cazul de a apela mf pentru a crea fişiere grafice ".*pk" pentru mărimi de font neprevăzute iniţial; în acest caz, para­metrii necesari vor fi determinaţi (cum vom arăta mai jos) în funcţie de valoarea "design size" (aici am păstrat pe cea implicită, 128pt) şi de mărimea fontului de bază al documentului LaTeX (ţinând cont în plus, de rezoluţia proprie dispozitivului de ieşire).

Am vrea ca boxele asociate caracterelor noastre să aibă aceleaşi dimensiuni (lăţime, înălţime, adâncime); centrul lemniscatei trebuie distanţat faţă de marginea stângă a boxei cu lungimea semiaxei şi în dreapta acestuia trebuie să "încapă" un cerc cu diametrul 2R:

wd# := (sax + 2R)*u#;  % lăţimea boxei
ht# := R*u#;  % înălţimea deasupra liniei de bază
dp# := R*u#;  % adâncimea (dedesubtul liniei de bază)

Alegem forma (preferând o aceeaşi formă, anume pencircle) şi grosimea "peniţelor" cu care să plotăm cercurile şi lemniscatele, respectiv diverse puncte (focarele, centrele de cercuri) şi linii (tangentele, raze) şi creem nişte variabile prin care să accesăm peniţele respective (încât să ne scutim de a re-crea ad-hoc structurile de date "pen") când va fi nevoie:

pickup pencircle scaled 1.1pt; path_pen := savepen;
pickup pencircle scaled 2.4pt; dot_pen := savepen;
pickup pencircle scaled 0.5pt; tan_pen := savepen;

Cu pregătirile de mai sus, putem începe să adăugăm în monics.mf definiţiile caracterelor noastre, folosind framework-ul beginchar...endchar pus la dispoziţie de către MF.

Definim două simboluri (hai să fie la indecşii 0 şi 30, din "tabela caracterelor") pentru lemniscata lui Bernoulli, diferind prin înclinarea axei acesteia faţă de orizontală (am ales 0° şi respectiv, 30°); construcţia decurge cum am arătat în [1] şi [3] [ conturăm o semibuclă, pe baza a trei puncte: un vârf în care tangenta este verticală (în cazul 0°), punctul "cel mai înalt" şi centrul lemniscatei; apoi simetrizăm această semibuclă faţă de axe ]; în plus, adăugăm "cadrul tangent" (folosind funcţia rectangle()) şi marcăm segmentul focarelor:

for Arg = 0, 30:  % lemniscată Bernoulli, rotită cu Arg în jurul centrului
beginchar(Arg, wd#, ht#, dp#);
    z2 = (sax*u, 0u);  % punctul z2 va fi centrul lemniscatei
    z3 = z2 - (xhi*u, F/2*u);  % cel mai "înalt" pe arcul inferior (prima buclă)
    path lower_left, tilda, lemniscate;
    lower_left = z2{left+down} .. z3 .. origin{up};  % bucla stângă, arcul inferior
    tilda = reverse(lower_left rotatedaround(z2, 180)) & lower_left;  % aduce cu '~'
    lemniscate = reverse(tilda reflectedabout(origin, z2)) & tilda;
    pickup path_pen;
    draw lemniscate rotatedaround(z2, Arg);  % roteşte cu Arg în jurul centrului
    pair focar[]; 
    focar[0] = (z2 + (F*u, 0u)) rotatedaround(z2, Arg);
    focar[1] = 2z2 - focar[0];  % (focarele fiind simetrice faţă de z2)
    pickup tan_pen; draw focar[0] -- focar[1];
    draw rectangle((0u, .5F*u), z2) rotatedaround(z2, Arg);
    pickup dot_pen; drawdot focar[0]; drawdot focar[1];
    currentpicture := currentpicture shifted(0, h/2);  % ridică faţă de linia de bază
endchar;
endfor

Definim cercurile prin origine (convenim să aibă codurile 16 şi 17) din care provin cele două lemniscate (folosim arrowz() pentru a marca raza prin origine):

code := 16;
for Arg = 0, 60:  % două cercuri prin origine; 'Arg' dă direcţia razei prin origine
beginchar(code, wd#, ht#, dp#);
    pair org; org = (sax*u, 0u);
    z1 = org + (R*u, 0u);
    z2 = z1 + (R*u, 0u);
    pickup path_pen; draw z2 .. org ..cycle;
    draw (org -- z1) rotatedaround(z1, Arg);  % raza prin origine a cercului
    draw arrowz(z1, Arg);
    currentpicture := currentpicture shifted(0, h/2);
endchar;
    code := 17;
endfor

În sfârşit, îmbinând cumva secvenţele de cod de mai sus, definim un caracter (având codul 8) reprezentând împreună o lemniscată şi cercul din care provine (am ales 15° ca direcţie a axei lemniscatei); pentru a vedea mai clar piesele componente, am mărit dimensiunile boxei şi în cursul construcţiei am folosit o unitate de măsură dublă faţă de cea iniţială (în plus, am evitat să mai adăugăm cadrul tangent lemniscatei):

beginchar(8, 2*wd#, 3*ht#, 1.5*dp#);  % lemniscată şi cercul din care provine
    v = 2u;  % dublăm vechea unitate de măsură
    Arg := 15;  % vom roti în jurul centrului cu 15 grade
    z2 = (sax*v, 0v);  % punctul z2 va fi centrul lemniscatei
    z3 = z2 - (xhi*v, F/2*v);  % cel mai "înalt" pe arcul inferior (prima buclă)
    path lower_left, tilda, lemniscate;
    lower_left = z2{left+down} .. z3 .. origin{up};  % bucla stângă, arcul inferior
    tilda = reverse(lower_left rotatedaround(z2, 180)) & lower_left;  % aduce cu '~'
    lemniscate = reverse(tilda reflectedabout(origin, z2)) & tilda;
    pickup path_pen;
    draw lemniscate rotatedaround(z2, Arg);  % lemniscata, rotită cu 'Arg'
    z5 = (R*cosd(30)*v, sind(30)*v);
    z1 = z2 + z5; z4 = z1 + z5;
    draw z4 .. z2 ..cycle;  % cercul din care provine lemniscata
    pair focar[]; 
    focar[0] = (z2 + (F*v, 0v)) rotatedaround(z2, Arg);
    focar[1] = 2z2 - focar[0];  % (focarele fiind simetrice faţă de z2)
    pickup tan_pen; draw focar[0] -- focar[1];  % segmentul focarelor
    pickup dot_pen; drawdot focar[0]; drawdot focar[1];
    pickup pencircle scaled 0.8pt;
    draw z2 -- z1; draw arrowz(z1, 30);  % raza prin origine a cercului
endchar;
end  % încheie fişierul "monics.mf"

Se cuvin încă unele mici precizări de termeni şi sintaxă (completând pe cele din [1-4]).
":=" care apare prin secvenţele de comenzi de mai sus este operatorul de atribuire, având semnificaţia obişnuită (în timp ce "=" are sensul din matematică, uzitat în egalităţi şi în ecuaţii). Apoi, left şi down desemnează punctele (sau vectorii) (-1, 0) şi (0, -1), încât specificaţia 'z2{left+down}' asigură că tangenta în punctul z2 are direcţia dată de vectorul (-1, -1) (adică, face 45° cu axa verticală). Iar "&" este un operator de alipire a două contururi care au un capăt comun (şi dacă este cazul - ca mai sus - putem folosi comanda reverse() pentru a aduce acel capăt comun în poziţia cerută: la sfârşitul primului contur şi la începutul celui de-al doilea).

Testarea directă a construcţiilor

Înainte de a ne gândi să folosim pachetul mnemonics în vreun document LaTeX (caz în care "monics.mf" ar fi compilat indirect, prin intermediul lui xelatex), să testăm direct (invocând mf de pe linia de comandă) simbolurile constituite mai sus. În acest scop, copiem "monics.mf" în directorul nostru de testări, ~/PROOF (v. [4]) şi comentăm linia "mode := ljfour;" (ne creem astfel posibilitatea comodă de a indica direct de pe linia de comandă, un mod de ieşire sau altul).

Modul 'proof' (prevăzut de MF exact în scopul examinării caracterelor create) reuşeşte numai pentru primele 4 caractere:

vb@Home:~/PROOF$ mf '\mode=proof; input monics'
This is METAFONT, Version 2.7182818 (TeX Live 2015/Debian) (preloaded base=mf)
(monics.mf [0] [30] [16] [17]
! Curve out of range.
.....
? x
Output written on monics.2602gf (4 characters, 59772 bytes).

Crearea ultimului caracter eşuează ("Curve out of range") fiindcă pixelii curbei capătă coordonate prea mari; MF are în vedere nu planul ca atare, ci doar coala obişnuită de hârtie şi consideră suficientă ca "valoare infinită" 2¹² = 4096 (pixeli); ori în modul 'proof', un punct este reprezentat pe 36 pixeli, încât unitatea de măsură (care în 'ljfour' avea 166 de pixeli) ajunge la u = 20*36 = 720 pixeli, devenind "enormă" pentru al cincilea caracter (v = 2*u = 1440 pixeli).

Putem examina totuşi primele patru caractere, folosind gftodvi (v. [3]) şi deschizând fişierul DVI rezultat, cu "Document Viewer"-ul obişnuit în Ubuntu:

vb@Home:~/PROOF$ gftodvi monics.2602gf 
vb@Home:~/PROOF$ evince monics.dvi 

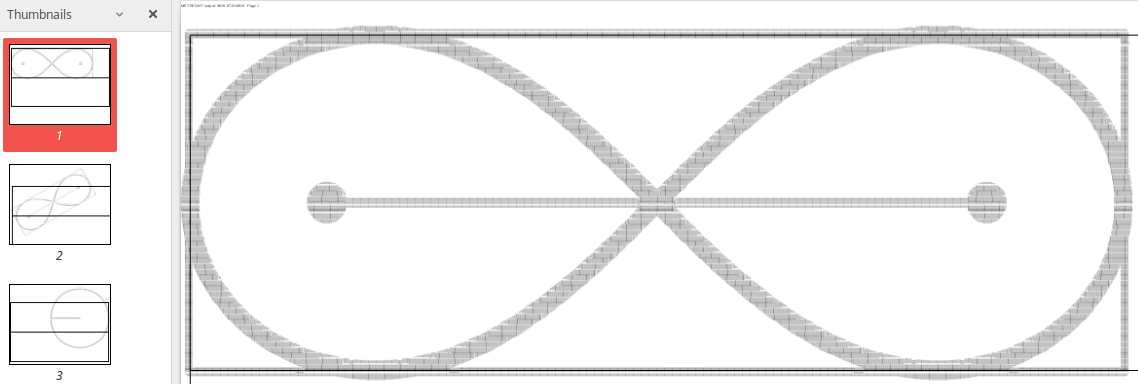
Am putea sesiza fel de fel de "defecte": lemniscatele au prea mult spaţiu în dreapta, iar cercurile au prea mult spaţiu în stânga (în cadrul boxelor, trasate cu linie continuă); primul caracter este situat în întregime deasupra liniei de bază (partea inferioară a boxei fiind vidă), iar celelalte "ies" deasupra boxei; lemniscata şi cadrul tangent ei se cam întretaie.

Dar primul "defect" este "intenţionat": am vrut să corelăm caracterele între ele, încât dacă am suprapune al treilea caracter peste primul (operaţie posibilă tocmai fiindcă am dimensionat la fel boxele aferente), atunci originea razei cercului va coincide cu centrul lemniscatei (analog pentru al doilea şi al patrulea caracter (neîncăput pe imaginea de mai sus, în cadrul din stânga)). De aici decurge şi al doilea "defect" dintre cele menţionate.

Al treilea defect este corijabil; cel mai simplu ar fi de mărit factorul 3 folosit în conturul produs de funcţia rectangle(); o soluţie mai bună (fiindcă face abstracţie de unitatea de măsură), constă în înlocuirea conturului respectiv prin: top lft A--top rt B--bot rt C--bot lft D--cycle, unde "top lft" este colţul stânga-sus al pixelului pătrat care are centrul în A, ş.a.m.d.; iar soluţia care probabil ar fi cea mai bună, constă în a renunţa la figurarea "cadrului tangent"…

Învăţămintele testării prin pdflatex a fontului 'mnem'

Următorul fişier LaTeX (o să-i zicem "simplu.test") prevede încărcarea pachetului mnemonics.sty şi afişarea caracterelor din fontul "mnem" definit de acesta:

\documentclass[12pt]{article}
    \usepackage{mnemonics}
\begin{document}
    $\bernu$ \quad $\circo$ \quad $\circorot$  \quad $\bernurot$ \quad $\circbern$
    
    \bigskip 
    \noindent nu se scrie "înjumătăţeşte", ci "\^{i}njum\u{a}t\u{a}\c{t}e\c{s}te"!
\end{document}

Am adăugat şi un mic paragraf conţinând un text arbitrar, pentru a vedea cam cum se corelează simbolurile noastre cu fontul de bază al documentului; dar am ales textul astfel încât să arătăm şi maniera generală de introducere a literelor cu un accent sau altul: comanda "\^{i}" dă litera ' î ', comanda "\u{a}" va produce litera ' ă ', etc. (mai jos vom folosi maniera "modernă", nu aşa de "generală", dar mult mai comodă).

Compilăm, fie cu pdflatex, fie cu xelatex:

vb@Home:~/4_art/Latex/aVB/9$ pdflatex simplu.test 

Am discutat deja în [2], unele dintre informaţiile afişate pe ecran în cursul compilării; întâi sunt încărcate şi operate definiţiile clasei de document 'article', pentru mărimea de font 12pt; apoi se încarcă mnemonics.sty şi (constatând că în directorul curent nu există un fişier "simplu.aux", dat fiind că este chiar prima compilare a fişierului tocmai înfiinţat) se încarcă şi începe să se opereze unics.fd. În final, se produce fişierul "simplu.pdf" (şi fişierul informativ "simplu.log") - de pe care am mărit (200%) şi am decupat această imagine (redată aici la 50%):

"simplu.log" sintetizează exemplar activitatea compilatorului şi dezvăluie intuiţiei logica lucrurilor. Aflăm întâi că pentru redarea textului s-a prevăzut fontul 'cmr12', din familia Computer Modern:

Missing character: There is no à in font cmr12!

În acest font lipsesc literele "accentuate"; însă TeX prevede macro-uri pentru formarea acestora: de exemplu, \accent21 g  - sau "scurtat" \u{g} - produce (în tabelul caracterelor lui 'cmr12', accentul adăugat aici literei indicate are codul 21).

vb@Home:~$ pdflatex nfssfont
... ...  %% informaţii privind 'pdflatex' şi 'nfssfont'
Input external font name, e.g., cmr10
\currfontname=cmr12
Now type a test command (\help for help):)
*\table
*\stop    % tabelul caracterelor este redat în "nfssfont.pdf"

Ceea ce urmează să ne lămurim, începe cu aceste mesaje informative:

LaTeX Font Info:    External font `cmex10' loaded for size
(Font)              <12> on input line 4.
LaTeX Font Info:    External font `cmex10' loaded for size
(Font)              <8> on input line 4.
LaTeX Font Info:    External font `cmex10' loaded for size
(Font)              <6> on input line 4.
LaTeX Font Info:    Try loading font information for U+nics on input line 4.

TeX permite introducerea de expresii matematice (oricât de complicate) cam la fel de uşor ca în cazul textului obişnuit, redarea grafică necesară fiind asigurată printr-un anumit "font matematic". Semnul "dollar" este destinat în TeX să marcheze expresii matematice; întâlnind acest semn pe linia a 4-a din "simplu.test", compilatorul trebuie să ia măsuri pentru a putea reda simbolurile matematice conţinute între semnele "dollar" şi în primul rând, încarcă fontul matematic existent în familia "Computer Modern", cmex10 (astfel că va putea crea pagina şi dacă încercarea anunţată mai sus "Try loading font information for U+nics" ar eşua).

Dar 'cmex10' a fost creat într-o singură variantă, anume numai pentru mărimea 10pt (însemnând că la această mărime caracterele respective vor arăta "cel mai bine"); fiind vorba acum de o altă mărime (anume 12pt), 'cmex10' a trebuit să fie scalat în momentul încărcării - operaţie care constă în multiplicarea coordonatelor punctelor cu raportul celor două mărimi (cu 12/10). Apoi, 'cmex10' este astfel scalat şi la mărimile de 8pt şi de 6pt. Necesitatea prezenţei acestor trei fonturi decurge din faptul că în formule (din matematică, fizică, chimie, etc.) apar frecvent indici şi exponenţi (care trebuie redaţi folosind caractere micşorate), iar pentru mărimea de bază 12pt indicii şi exponenţii sunt redaţi (de regulă) la 8pt, iar "subindicii" la 6pt.

Există şi comenzi corespunzătoare acestor "scalări", \scriptstyle{<expresie>} şi respectiv \scriptscriptstyle{<expresie>}, analoge comenzilor de redimensionare din modul text \tiny, \footnotesize, \large, \huge etc.; dacă ar întâlni a asemenea comandă în fişierul pe care îl compilează, pdflatex (ca şi xelatex) va lansa eventual mf pentru a genera un fişier grafic ".*pk", prin scalarea la mărimea indicată ("script", "large", etc.) a fişierului grafic de bază.

Mai departe, se încarcă şi se operează fişierul "unics.fd" (punând în practică intenţia anunţată, "Try loading font information for U+nics"):

(./unics.fd)  %% \DeclareFontShape{U}{nics}{}{}{<-> [3] monics}{}
LaTeX Font Warning: Font shape `U/nics//' will be
(Font)              scaled to size 36.0pt on input line 4.
LaTeX Font Warning: Font shape `U/nics//' will be
(Font)              scaled to size 24.0pt on input line 4.
LaTeX Font Warning: Font shape `U/nics//' will be
(Font)              scaled to size 18.0pt on input line 4.

Fiindcă \DeclareFontShape din "unics.fd" indică în specificaţia de mărime factorul 3, urmează ca formele grafice respective să fie "scalate" la mărimile 36pt (= 3×12pt, ca mărime de bază pentru expresii cuprinse între caractere "dollar"), respectiv (dar aceasta, când va fi cazul) la 24pt (pentru \scriptstyle, 3×8pt) şi 18pt (mărimea pentru \scriptscriptstyle, 3×6pt).

Apoi, fiindcă nu găseşte fişierul metric monics.tfm şi fişierul grafic monics.600pk (fiind vorba de prima compilare a lui "simplu.test"), pdflatex apelează mf pe fişierul monics.mf, generând astfel cele două fişiere care lipseau (dar se generează monics.600gf; conversia la ".*pk" va fi făcută spre finalul procesului, pentru toate fişierele ".*gf" generate pe parcurs).

După cum am fost informaţi ("will be scaled to size ...") ar urma acum ca monics.600pk să fie "scalat" la 36pt şi eventual, la 24pt şi 18pt; dar fiindcă în "simplu.test" nu apar comenzi ca \scriptsize sau \scriptscriptsize (şi nici \large, etc.) - se generează (reapelând mf) doar fişierul grafic pentru mărimea principală (36pt), anume monics.169pk.

Rezoluţia de 169 "pixels per inch" a rezultat după regula de scalare explicată mai sus, ţinând seama de faptul că pentru fontul nostru am păstrat "design size" cu valoarea implicită 128pt; factorul de scalare este 36/128 = 0.28125 şi rezoluţia iniţială fiind de 600dpi, urmează că în urma scalării vom avea 0.28125×600dpi = 168.75 ≈ 169 "pixels per inch".

Fişier LaTeX pentru testarea şi documentarea fontului 'mnem'

Redăm un fişier LaTeX mai amplu, prin care documentăm cumva fontul "mnem" şi mnemonicele pe care le reprezintă. Vizăm de această dată xelatex (nu pdflatex, ca mai sus), încât incluzând pachetul fontspec nu mai este nevoie (în general) să folosim comenzi TeX de producere a literelor cu accent [ fiind recunoscută maniera de folosire a tastaturii pe care am instituit-o la nivelul siste­mului Ubuntu-Linux: literele cu accent ca 'ă', 'ş', etc. pot fi tastate direct, "prefixând" tastarea literei subiacente (fără accent) cu acţionarea tastei 'Alt'-dreapta ].

\documentclass[12pt]{article}
\usepackage{mnemonics}

\usepackage[no-math]{fontspec}
\usepackage{xcolor}

\newcommand\transdef{\ensuremath{\mathrel{\stackrel{\sqrt z}{\longrightarrow}}}}

\pagestyle{empty} \topmargin -1in \headsep 10pt \footskip 0pt
\begin{document}
{\em Lemniscata lui Bernoulli\/} {\color{blue}$\bernu$} are centru de simetrie; 
tangentele în centru bisectează axele; alte două tangente sunt verticale şi alte 
două sunt orizontale, iar raportul laturilor cadrului tangent format de ele este 
$2\sqrt{2}$.

În plus (de fapt, proprietatea definitorie obişnuită), există două puncte pe axa 
orizontală, simetrice faţă de centru, astfel încât produsul distanţelor faţă de 
acestea ale oricărui punct al curbei este constant.

\bigskip
Considerăm un cerc care trece prin originea fixată $O$ şi are raza $\rho$; pentru 
fiecare punct $M$ al său, găsim primul punct de intersecţie al razei $OM$ cu 
cercul de centru $O$ şi rază $\sqrt{\rho\,}$ şi îl rotim în jurul lui $O$ cu 
jumătatea unghiului polar al lui $M$. Altfel spus (văzând punctele ca numere 
complexe), aplicăm punctelor cercului considerat funcţia complexă "radical de 
ordinul doi". Obţinem astfel, lemniscata Bernoulli centrată în origine şi având 
ca focare cele două puncte rezultate aplicând transformarea menţionată centrului 
cercului dat. Adică, într-o formulare mnemonică:
$${\color{blue}
   \hbox{\Large{$\circo\transdef\bernu\qquad\circorot\transdef\bernurot$}}}$$
\noindent\lq\lq{\color{blue} Radicalul unui cerc care trece prin origine este o 
lemniscată Bernoulli\/}\rq\rq{} centrată în origine; direcţia axei înjumătăţeşte 
direcţia razei prin origine.

\bigskip
\reversemarginpar\mbox{}\marginpar{fontul \\ {\color{blue}mnem}}
\begin{tabular}{r l c| c c c}
\emph{Code} & \emph{Command} & \emph{Glyph} \\
0 & \verb"$\bernu$" & $\bernu$ & \hbox{\large{$\bernu$}}  
                    & \hbox{\Large{$\bernu$}} & \hbox{\huge{$\bernu$}}\\ \hline\\
30 & \verb"$\bernurot$" & $\bernurot$ & \hbox{\large{$\bernurot$}} 
              & \hbox{\Large{$\bernurot$}} & \hbox{\huge{$\bernurot$}}\\ \hline\\
16 & \verb"$\circo$" & $\circo$ & \hbox{\large{$\circo$}} 
                    & \hbox{\Large{$\circo$}} & \hbox{\huge{$\circo$}}\\ \hline\\
17 & \verb"$\circorot$" & $\circorot$ & \hbox{\large{$\circorot$}} 
              & \hbox{\Large{$\circorot$}} & \hbox{\huge{$\circorot$}}\\ \hline\\
8 & \verb"$\circbern$" & $\circbern\quad$ & {\large \emph{large}} 
                       & {\Large \emph{Large}} & {\huge \emph{huge}}
\end{tabular}

\noindent Cercurile prin origine au ca rădăcini lemniscate Bernoulli: 
${\color{blue}\hbox{\large{$\circbern$}}}$.\\ 
Axa focarelor bisectează unghiul polar al centrului cercului.
\end{document}

De data aceasta (spre deosebire de fişierul LaTeX anterior, "simplu.test") am folosit şi comenzi de modificare a mărimii simbolului (în linia 31 şi în coloanele 4–6 ale tabelului de caractere); desigur, am evitat micşorarea (ca \scriptstyle) fiindcă nu ar avea sens ca vreunul dintre cele 5 simboluri de aici să apară ca indice, în vreo expresie.
Dintre mesajele informative emise de xelatex când întâlneşte asemenea comenzi (\Large, \huge etc.), să le considerăm pe cele asociate liniei 31:

LaTeX Font Info:    External font `cmex10' loaded for size
(Font)              <17.28> on input line 31.
LaTeX Font Warning: Font shape `U/nics//' will be
(Font)              scaled to size 51.84pt on input line 31.

Decupăm aici linia 31, separând cumva acoladele:

$${\color{blue}
   \hbox{\Large
            {$\circo\transdef\bernu\qquad\circorot\transdef\bernurot$}
        }
  }$$

Dublând "dollar" (la începutul şi la sfârşitul expresiei), se creează un context matematic special, expresia ambalată fiind redată în centrul unui paragraf separat, cu o anumită spaţiere verticală. \Large nu se poate folosi direct pentru expresii matematice, încât am constituit un context \hbox\Large{$...$} (în jurul simbolurilor pe care vrem să le mărim).
'\transdef' este o comandă pe care am definit-o în preambulul documentului şi are ca efect o anumită îmbinare a două simboluri: cel pentru "radical" este aşezat deasupra unei săgeţi (semnificând "transformarea prin radical"); aceste simboluri vor fi redate din fontul matematic cmex10, pe care compilatorul îl va încărca scalat la mărimea 17.28pt (dat fiind că simbolurile trebuie redate sub efectul \Large, care pentru fontul de bază 12pt devine 17.28pt).

Conform ultimului dintre mesajele informative redate mai sus, compilatorul încearcă să scaleze şi simbolurile noastre, anume la mărimea 3×17.28 = 51.84pt (unde factorul 3 a fost dictat de \DeclareFontShape din "unics.fd"). Pentru aceasta, va apela mf cum am arătat anterior şi va genera fişierul grafic monics.243pk; într-adevăr, având "design size" de 128pt şi rezoluţia de ieşire de 600dpi, rezultatul va avea 51.84×600/128 = 243 pixels per inch.

La fel va proceda xelatex şi pentru \large şi \huge, întâlnite în definiţia tabelului de la sfârşitul fişierului - rezultând încă, fişierele grafice monics.202pk şi respectiv monics.350pk.

Pentru "tabelul caracterelor" –fiindcă avem numai 5 caractere– am folosit mediul tabular, încolonând după cod, comanda de acces şi mărimea "glyph"-ului. Dar într-o formă standard (când sunt multe "glyph"-uri), tabelul caracterelor se obţine folosind (interactiv) pdftex (dar nu pdflatex) cu programul lui Knuth testfont:

vb@Home:~/4_art/Latex/aVB/9/docer_mnem$ pdftex testfont
This is pdfTeX, Version 3.14159265-2.6-1.40.16 ... (preloaded format=pdftex)
...
Name of the font to test = monics
Now type a test command (\help for help):)
*\table
*\end    %% Output written on testfont.pdf (1 page, 55541 bytes).

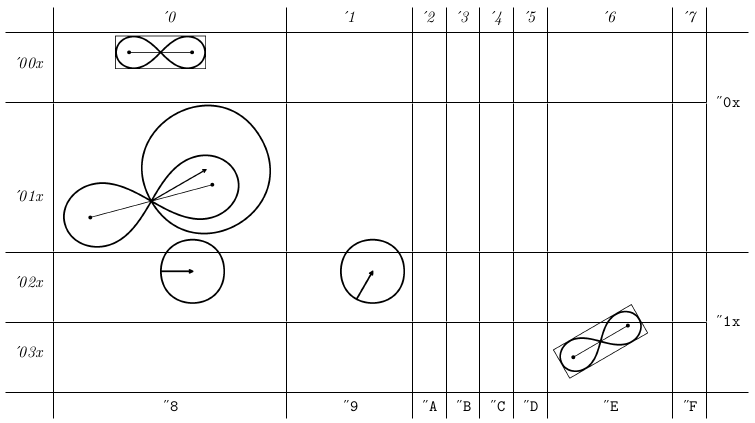
Intrările în tabel (maximum 256) sunt marcate în stânga şi sus în sistemul octal (astfel, "lemniscata rotită" are codul '036, adică în zecimal: 3×8+6=30), iar în dreapta şi jos în sistemul hexazecimal (''1E, adică în zecimal: 1×16+14=30); pentru etichetare s-a folosit familia de fonturi CM ("Computer Modern"). Pe baza acestui tabel putem aprecia comparativ mărimea "glyph"-urilor precum şi încadrarea fiecăruia în boxa corespunzătoare; dar pentru aceasta, cel mai bine era să fi alocat codurile astfel încât în acest tabel să nu apară două caractere pe o aceeaşi linie sau coloană; de exemplu, pentru codurile '0xx, cu x=0..4, simbolurile ar fi fost aşezate pe diagonala tabelului şi boxa din tabel ar corespunde exact (făcând abstracţie de un anumit factor comun de scalare) boxei asociate de TeX (în cursul procesului de construcţie a şablonului paginii).

Am mai precizat anterior, că TeX construieşte de fapt "şablonul paginii" (utilizând informaţia din fişierele metrice ".tfm"): prevede pentru fiecare caracter boxa în care va fi aşezat "glyph"-ul respectiv, constituie câte o boxă pentru fiecare cuvânt (aliniind orizontal boxele caracterelor componente) şi apoi pentru fiecare linie de text, aliniind vertical după anumite reguli pentru a forma boxele corespunzătoare paragrafelor de text şi apoi boxa corespunzătoare unei întregi pagini. Încastrarea formelor grafice în boxele rezervate astfel, va reveni programelor de redare DVI sau PDF (rezidente eventual chiar pe imprimanta care va tipări documentul final), utilizând informaţiile din fişierele grafice ".pk".

Fişierul monics.tfm este un fişier binar în care mf plasează informaţiile dimensionale prevăzute în monics.mf; putem folosi programul tftopl ("tfm"-"to"-"properties list") pentru a "vedea" fişierul binar respectiv:

vb@Home:~/4_art/Latex/aVB/9/docer_mnem$ tftopl monics.tfm
(DESIGNSIZE R 128.0)
(COMMENT DESIGNSIZE IS IN POINTS)
(COMMENT OTHER SIZES ARE MULTIPLES OF DESIGNSIZE)
(CHECKSUM O 11741734766)
(CHARACTER O 0
   (CHARWD R 0.533471)  lăţime
   (CHARHT R 0.15625)   înălţime
   (CHARDP R 0.15625)   adâncime
   )
(CHARACTER O 10
   (CHARWD R 1.066942)
   (CHARHT R 0.46875)
   (CHARDP R 0.234375)
   )
... etc.

Pentru o mică verificare: în monics.mf fixasem ca lăţime pentru caracterul de cod 0, wd# := (sax + 2R)*u# (unde R=1, F=sqrt(R)=1, sax=F*sqrt(2)=sqrt(2) şi u# := 20pt#), încât avem wd# = (sqrt(2) + 2)*20 ≈ 68.28427, ceea ce corespunde (cu eroare neglijabilă) termenilor redaţi mai sus, DESIGNSIZE×CHARWD = 128*0.533471=68.28429.