Are sens să desenezi ceva după o fotografie, dacă după un timp descoperi "ceva" deosebit în cadrul ei; o pălărie care acoperă, sub nişte ochelari şi un păr bogat, un chip feminin sprijinit pe palma strânsă în pumn şi un cot aşezat gingaş pe masă - poate sugera un moment de linişte şi detaşare nepământeană; desigur, vei ignora alte elemente din poză (scaune, pahare, etc.) şi vei încerca să desenezi, să scrutezi şi să-ţi asumi acel rar (implicit subiectiv) "ceva".

În principiu, ca să desenezi ceva după o fotografie, ai proceda cam aşa: ai contura uşor pe coala de desen un cadru dreptunghiular potrivit (o "boxă"); ai gândi nişte corelaţii şi ai marca pe coală câteva puncte de reper (de exemplu, ai putea observa că linia exterioară a cotului şi linia stângă a feţei de sub pălărie sunt aliniate aproximativ pe o diagonală a boxei, intersectându-se cam în centrul acesteia, unde apare mâna strânsă în pumn pe care se sprijină faţa; pălaria are un bord larg, cam la baza primei treimi a boxei, sub care se văd parţial ochelarii şi are o panglică neagră groasă, fiind aproape centrată pe lăţime); vei reflecta poate şi mai mult, asupra corelaţiilor dintre pălăria cu panglică neagră, părul bogat şi el negru, ochelari şi faţa triunghiulară diafană îmbinată antebraţului cu pumnul strâns care sprijină faţa - şi la un anumit moment, vei începe să "uneşti" punctele marcate, folosind anumite creione şi haşuri.

Din fericire (că altfel piaţa artei ar dispărea), lucrurile nu se rezumă aşa de simplu: "alege câteva puncte de reper şi nişte creioane, apoi uneşte-le"; esenţial, distinctiv şi greu de învăţăt este să ţii creionul în mână (şi pe de altă parte, să vezi "ceva"). Însă în principiu, orice amator poate urma până una-alta, strategia de lucru ilustrată –îndrăzneţ, desigur– mai sus.

Din fericire –sau nu, fiindcă lucrurile marşează fără sfârşit în contexte dinamice, inhibate din când în când de considerente mercantile– Metafont chiar aşa de "simplu" procedează: fixează nişte dimensiuni de încadrare (în corelaţie cu un grup prestabilit de parametri dimensionali, menit să caracterizeze tipografic un ansamblu de litere) şi descrie corpul fiecărei litere sau simbol din fontul respectiv prin definirea câtorva puncte de reper şi prin indicarea unui anumit tip de "peniţă" de trasare - rezultând printr-o interpretare proprie (un anumit tip de interpolare), "harta de pixeli" necesară imprimantei (sau display-ului) pentru a reda caracterul respectiv.

Având date două puncte, Metafont va completa spaţiul dintre ele în cel mai simplu şi frumos mod: fie printr-o linie dreaptă, fie printr-un semicerc; iar indicarea unui al treilea punct, sau precizarea direcţiilor dorite pentru tangentele în capete, conduce la un arc de curbă netedă între punctele respective (evitând pe cât se poate, punctele unghiulare).

Lemniscata lui Bernoulli (referită mai departe prin $\mathcal{B}$) este curba care are (în raport cu axele ei) ecuaţia (carteziană şi respectiv parametrică): $$(x^2+y^2)^2=d\,(x^2-y^2)\quad(d>0)$$ $$x=\frac{\sqrt{d\,}\cos\theta}{1+\sin^2\theta},\quad y=\frac{\sqrt{d\,}\cos\theta\sin\theta}{1+\sin^2\theta}$$

De obicei, obţinem graficul printr-un program (în R, sau Python - v. de exemplu [2]) în care se determină şi se plotează un număr cât mai mare de puncte "vecine" care satisfac ecuaţia curbei. Graficul lui $\mathcal{B}$ seamănă cu simbolul pentru "infinit" ($\infty$, sau ∞) - dar… nu ne mulţumim cu această asemănare; cu Metafont putem obţine un simbol "perfect" pentru $\mathcal{B}$, indicând cum vom vedea mai jos, doar trei puncte (şi direcţiile tangentelor la grafic în aceste trei puncte).

Bineînţeles că întâi am încercat cu numai două puncte (dar rezultatul este departe de "perfect"):

screen_cols := 1366; screen_rows := 768;  % (în fişierul 'modes.mf')
rulepen := nullpen;  % anulăm aici, trasarea boxei obişnuite
beginchar(0, 30pt#, 5pt#, 5pt#);
    pickup pencircle;  % "peniţă" foarte subţire, cu care vom simula curba
    z1 = (.2w, 0); z2 = (.5w, 0);
    path quart; quart = z2{dir225}..z1{dir90};  % traseul unui "sfert" al curbei
    draw quart;  % desenează sfertul, apoi simetrizează faţă de axe
    draw quart reflectedabout(z1, z2);
    addto currentpicture also currentpicture rotatedaround(z2, 180);
% endchar %% Dar amânăm încheierea definiţiei, intercalând o verificare:
          %% marcăm z1,2 şi trasăm prin 91 puncte exacte, un sfert al curbei
pickup pencircle scaled 0.15pt;
drawdot(z1); drawdot(z2);
pair k[];
D := length(z2-z1);  % v. mai sus, ecuaţia curbei
for i=0 upto 90:
    x := D*(cosd i)/(1+(sind i)**2);
    y := x*(sind i);
    k[i] := z2 + (x, y);  % referă punctele curbei faţă de centrul ei (z2)
endfor
quart := k[0] for i=0 upto 90: -- k[i] endfor -- k[90];
pickup pencircle scaled 0.06pt;  % o peniţă mai groasă (pentru curba "exactă")
draw quart;
          %% v. figura; arcul simulat diferă sensibil de cel exact
endchar;

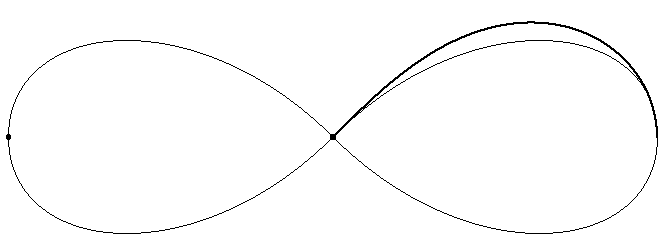
Mai întâi, draw z2{dir225}..z1{dir90}; a unit printr-un arc punctele z2 (centrul intenţionat al curbei) şi z1 (aflat în stânga), astfel încât faţă de axa orizontală, tangentele în capetele arcului să fie înclinate cu 225° şi respectiv, cu 90° (am avut în vedere faptul că $\mathcal{B}$ este tangentă în centru la bisectoarele sistemului de axe şi are tangente verticale în vârfurile de pe axa orizontală). Apoi, folosind reflectedabout() şi rotatedaround() am simetrizat acest arc faţă de orizontală, obţinând bucla din stânga şi am simetrizat această buclă faţă de verticală.

Curba finală rezultată astfel diferă însă prea mult, faţă de $\mathcal{B}$ - cum am atestat prin secvenţa de verificare adăugată în programul de mai sus. Am ales factorul "$\sqrt{d\,}$" din ecuaţiile parametrice ale lui $\mathcal{B}$ ca fiind distanţa D:=length(z2-z1) - pentru a avea acea lemniscată care are aceleaşi vârfuri (pe orizontală) ca şi curba rezultată în prima parte a programului; trebuie observat că implicăm o translaţie orizontală (în linia "k[i] := z2 + (x, y)"), încât originea (0,0) asumată de ecuaţia standard pentru $\mathcal{B}$ drept centru al curbei, să ajungă în centrul z2 al curbei trasate aici.

Metafont consideră gradul (şi nu radianul) ca unitate de măsură a unghiurilor, iar funcţiile trigonometrice obişnuite devin cosd() şi sind(). Prin "for i=0 upto 90: ... endfor" (din grad în grad) am generat din ecuaţiile parametrice, 91 de puncte (x, y) ale curbei $\mathcal{B}$ şi le-am unit cu "segmente", constituind un nou traseu "quart" (operatorul "--" uneşte punctele prin segmente, iar ".." - prin "arce frumoase"); am trasat "sfertul" de curbă $\mathcal{B}$ generat astfel folosind o "peniţă" mai groasă - rezultând arcul îngroşat de deasupra buclei din dreapta din figura de mai sus, cu o diferenţă evidentă faţă de arcul simulat (şi trasat subţire) în prima parte a programului.

Prin urmare, nu este suficient să fixăm doar două puncte (şi cele două direcţii de tangenţă), pentru ca Metafont să producă suficient de fidel, o curbă $\mathcal{B}$. Să luăm în calcul un al treilea punct: pare firesc (confruntând arcul îngroşat cu cel subţire aflat dedesubt) să alegem unul dintre punctele cel mai "înalte" ale curbei - deci alegem acel punct de pe arcul care uneşte z1 cu z2, în care tangenta la $\mathcal{B}$ devine orizontală.

Ştim desigur, că punctele de extrem ale unei funcţii sunt rădăcinile derivatei acesteia; să derivăm (în raport cu $x$, pentru $x\ne 0$) ecuaţia de mai sus a curbei $\mathcal{B}$: $$2(x^2+y^2)(2x+2yy')=d(2x-2yy')$$

De aici, găsim uşor că $$y'=\frac{x(d-2x^2-2y^2)}{y(d+2x^2+2y^2)}$$

şi avem $y'=0$ pentru acele puncte pentru care $x^2+y^2=d/2$.

Cu alte cuvinte, cercul de rază $\sqrt{d/2}\,$ cu acelaşi centru ca şi lemniscata, intersectează $\mathcal{B}$ în punctele cel mai "înalte". Dar punctele de abscise $\pm \sqrt{d/2}$ sunt chiar focarele lemniscatei $\mathcal{B}$, adică acele puncte fixe $F, F'$ pentru care produsul distanţelor la acestea ale oricărui punct al curbei este constant. Rezultă această proprietate a lemniscatei lui Bernoulli: cercul cu diametrul $FF'$ o intersectează în punctele cel mai "înalte" ale acesteia.

Să mai observăm că $y'$ ajunge ∞ în $y=0$ - adică în punctele sale de pe axa orizontală, $\mathcal{B}$ are tangente verticale (cum am indicat mai sus, prin z1{dir 90}); iar un raţionament intuitiv simplu confirmă că $\mathcal{B}$ are drept tangente în centrul său, cele două bisectoare: dacă $x$ şi $y$ tind "uniform" spre 0, atunci le putem considera "$\pm$egale" (pot diferi ca semn) în vecinătatea originii şi după simplificările corespunzătoare ne rămâne la limită $y'=\pm\frac{d}{d}=\pm 1$ (pantele bisectoarelor).

Rezolvând sistemul de ecuaţii aferent lui $\mathcal{B}$ şi cercului relevat mai sus, găsim că punctele de extrem căutate (cel mai "înalte" ale lui $\mathcal{B}$) sunt: $$\small\left(\pm\sqrt{\frac{3d}{8}}, \pm\sqrt{\frac{d}{8}}\,\right)$$

Desigur - să nu uităm că în cazul nostru mai avem de făcut o translaţie orizontală (centrul curbei pe care o vrem de la Metafont fiind în z2). Avem astfel al treilea punct, cum ne propusesem, şi acum putem rescrie programul de mai sus:

beginchar(0, 30pt#, 5pt#, 5pt#);
    pickup pencircle;
    z1 = (.2w, 0); z2 = (.5w, 0);
    D := length(z2-z1); pair high; path quart;
    high = (.5*D*sqrt(1.5), .5*D/sqrt(2));  % punctul cel mai "înalt"
    z3 = z2 - high;  % "high" pe arcul inferior al primei bucle
    quart = z2{dir225} .. z3 .. z1{dir90};  % arcul inferior al primei bucle
    draw quart;
    draw quart reflectedabout(z1, z2);  % rezultă bucla din stânga (prima)
    addto currentpicture also currentpicture rotatedaround(z2, 180);
    %% secvenţa de verificare din primul program %% 
endchar;

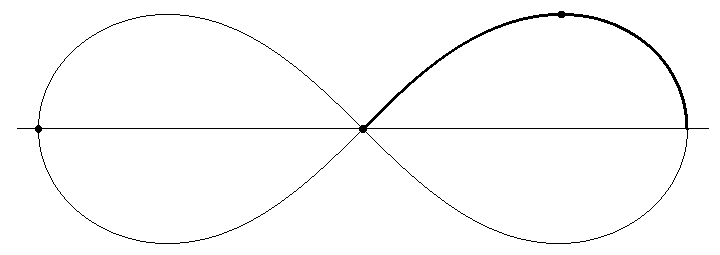
De data aceasta, Metafont a produs exact graficul lui $\mathcal{B}$ (să evităm obsesia erorilor de rotunjire inerente) şi încă ar fi de subliniat că am indicat doar trei puncte şi direcţiile tangentelor în capete (în punctul intermediar z3 am omis să mai precizăm direcţia 0° a tangentei, lăsând Metafont să aleagă pe cea mai potrivită). Explicaţia lapidară a acestui succes ar fi simplă: lemniscata lui Bernoulli este o curbă frumoasă, iar Metafont tocmai aceasta "ştie" să facă, pe baza a doar câtorva indicaţii: linii frumoase (alte programe s-ar plânge: "prea puţine puncte").

În "partea a II-a" urmează să lămurim cum folosim programe precum cele redate mai sus, vizând mf (interpretorul şi compilatorul de Metafont); urmează să adoptăm dimensiuni obişnuite pentru un font (aici le-am exagerat, pentru a ne facilita investigaţia) şi să vedem cum putem folosi caracterul creat alături de caracterele fontului curent, în cadrul unui document LaTeX.