Metafont pentru lemniscata lui Bernoulli (partea a treia)
[1] Metafont pentru lemniscata lui Bernoulli (partea întâia)
[2] Metafont pentru lemniscata lui Bernoulli (partea a doua)
Evocăm întâi, de unde am plecat:
## program R: generează şi plotează un cerc aleatoriu care trece prin origine ## şi apoi, transformatul acestuia prin funcţia complexă sqrt() n <- 3000 arcs <- seq(0, 2*pi, length=n) # n=3000 puncte echidistante pe [0, 2*Pi] fi <- sample(arcs, 1) # o direcţie aleatorie ('fi' radiani) r <- 0.75 # raza cercului (arbitrară) plot(0, type="n", xlim=c(-2*r, 2*r), ylim=c(-2*r, 2*r), asp=1, xlab="", ylab="", bty="n", xaxt="n", yaxt="n") # setează o fereastră grafică C <- r*exp(1i*arcs) # 'C': cerc de rază 'r' centrat în origine z0 <- r*exp(1i*fi) # 'z0': un punct aleatoriu pe cercul 'C' points(z0, cex=0.5, pch=19) C0 <- z0 + C # 'C0': cerc (centrat în 'z0') care conţine originea axelor points(C0, type="l", lwd=0.5) C0r <- sqrt(C0) # "radicalul cercului 'C0'" (este o lemniscată Bernoulli) points(c(C0r,-C0r), cex=0.001)
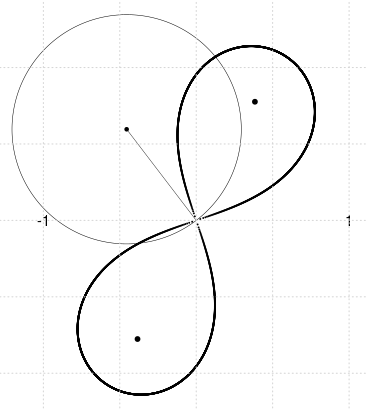
Am demonstrat (v. "Radicalul cercului") că aplicând funcţia complexă $\sqrt{z\,}$ punctelor unui cerc care trece prin originea planului (complex) se obţine o lemniscată Bernoulli ($\,\mathcal{B}\,$); axa acesteia bisectează unghiul polar al centrului cercului, iar pătratul distanţei focale este dublul diametrului cercului (mai precis, focarele sunt $\small\,\pm\sqrt{z_0}$ unde $\small z_0$ este afixul centrului cercului). Am inventat desigur, o exprimare mnemonică: radicalul unui cerc prin origine este o lemniscată Bernoulli.
Pentru grafice, în programul R de mai sus am folosit un număr suficient de mare de puncte (3000, sau şi mai multe); dar în [1] am arătat ("practic", deocamdată) că dacă am folosi Metafont, atunci sunt suficiente numai (anumite) trei puncte, pentru a obţine un grafic $\mathcal{B}$. Desigur, am ajuns la Metafont manifestând dorinţa de a simboliza exprimarea amintită: am avea nevoie de un simbol grafic pentru $\mathcal{B}$ şi probabil, de unul pentru "cerc care trece prin origine" (pentru "radical" putem folosi simboluri existente deja, în diverse fonturi matematice).
Raza cercului este parametrul de bază (corelarea simbolurilor)
Fie $\varphi$ direcţia razei prin origine a cercului (altfel spus, măsura unghiului polar al centrului cercului - variabila 'fi' din programul redat mai sus). Vrem să reflectăm separat două cazuri: cel "banal", când $\varphi=0$ şi respectiv, cazul ceva mai general când de exemplu, $\varphi=\pi/3$. În cazul "banal" cercul este tangent în origine axei verticale $\small Oy$, iar axele $\small Ox$ şi $\small Oy$ sunt chiar axele de simetrie ale lui $\mathcal{B}$; cazul "ceva mai general" va rezulta rotind în jurul originii cercul şi $\mathcal{B}$ din poziţia "banală", cu unghiul $\varphi$ şi respectiv cu unghiul $\varphi/2$.
Vom nota cu $\small\mathsf{R}$ raza cercului şi cu $\small\mathsf{F}$ distanţa de la origine la un focar al lui $\mathcal{B}$; avem $\small\mathsf{F}=\sqrt{\mathsf{R}\,}$. Semiaxa lui $\mathcal{B}$ este $\small\mathsf{F}\sqrt{2\,}$ şi punctele sale cel mai "înalte" (cel mai depărtate de linia focarelor) sunt distanţate cu $\small\mathsf{F}/2$ faţă de axa focarelor şi cu $\small\mathsf{F}\sqrt{3\,}/2$ faţă de mediatoarea segmentului determinat de focare (v. [1]).
Prin urmare, vom demara construcţia simbolurilor respective plecând de la o valoare potrivită pentru $\small\mathsf{R}$; vrem desigur, ca aceste simboluri să poată figura într-un document LaTeX (alături de caracterele din fontul de bază) - încât va trebui să vedem şi cum dimensionăm în funcţie de $\small\mathsf{R}$ (şi probabil, de mărimea fontului de bază), boxele pe care TeX le va asocia simbolurilor noastre.
Instrucţie pe compilatorul MF (construcţia unei semibucle)
Tatonăm cumva, programul mf - compilatorul (şi interpretorul) de Metafont ("MF"); alegem să experimentăm pe seama curbei $\mathcal{B}$ (cazul cercului ar fi desigur, "banal").
Am arătat în [1] că pentru a construi (cu MF) o semibuclă a lui $\mathcal{B}$ avem nevoie (doar) de 3 puncte: centrul $z_0$ al lemniscatei, intersecţia $z_1$ cu $\small Ox$ şi punctul cel mai "înalt" $z_2$; trebuie doar să mai precizăm direcţia tangentei în $z_0$ (anume ±45°, sau 180°±45° - depinzând de sensul în care trasăm arcul) şi direcţia tangentei în $z_1$ (±90°). $\mathcal{B}$ se va putea obţine simetrizând faţă de axe, semibucla astfel construită. (Desigur, putem proceda asemănător pentru a obţine un cerc)
Alegem $\small\mathsf{R}$ = 3600; semidistanţa focală va fi $\small\mathsf{F}=\sqrt{\mathsf{R}\,}$ = 60 de pixeli, iar semiaxa va fi (rotunjind) $\small\mathsf{F}\sqrt{2\,}$ = 85 de pixeli. Alegând $z_0$ la 100 de pixeli faţă de marginea stângă şi 50 de pixeli faţă de marginea superioară, ne asigurăm că întreaga lemniscată va "încăpea" pe ecran (sau pe coala de hârtie, în vreun alt caz; vom mai vedea încolo ce înseamnă "pixel" pentru MF, după caz):
%% fişierul "firstquart.mf" R = 3600; F = sqrt(R); z0 = (100, 50); % centrul lemniscatei z1 = z0 + (F*sqrt(2), 0); % capătul semiaxei pozitive z2 = z0 + .5(F*sqrt(3), F); % cel mai înalt pe semibucla dreapta-sus path firstq; % declară curba 'firstq' (variabilă de tip "path") firstq = z0{dir 45} .. z2 .. {dir -90}z1; % "primul sfert" al lemniscatei
Lansăm programul mf, indicându-i fişierul de comenzi tocmai redat:

La promptul '*' se poate tasta o nouă comandă; dacă tastăm bye sau end, atunci mf îşi va încheia execuţia, înregistrând sesiunea de lucru respectivă în fişierul "firstquart.log" (ulterior, din acest fişier vom putea recupera comenzi dintre cele încercate rând pe rând la promptul '*', constituind cu ele un fişier de comenzi –mai convenabil de folosit– precum cel redat mai sus).
Dacă tastăm show(firstq);end atunci vom găsi în fişierul ".log" o detaliere a construcţiei curbei 'firstq'; operatorul ".." – sau "path_join", cum îl numeşte MF – interpolează între nodurile indicate (după un algoritm care angajează curbe Bézier cubice), iar arcul respectiv este în final o listă înlănţuită de puncte (şi alte informaţii). Comanda draw va asocia fiecărui punct din această listă câte o anumită structură de pixeli, în funcţie de tipul de "peniţă" specificat în prealabil; rezultatul va fi înregistrat în variabila internă 'currentpicture'.
Setând (înainte de draw) variabile interne ca 'tracingedges' (sau 'tracingoutput', etc.) putem obţine informaţii despre aceste structuri de date; în loc de a tasta direct la promptul "*", preferăm să completăm secvenţa de comenzi din "firstquart.mf":
pickup pencircle; % alege o "peniţă" de trasare (circulară, subţire) tracingedges := 1; %% := 2 pt. informaţii amănunţite (şi complicate!) draw firstq; % şi înregistrează 'firstq' în variabila 'currentpicture' show(currentpicture); end
Relansând mf pentru fişierul de comenzi astfel completat, vom obţine în fişierul ".log":
(firstquart.mf Tracing edges at line 12: (weight 1) %% [currentpicture] (101,50)(101,51)(102,51)(102,52)(103,52)(103,53)(104,53)(104,54)(105,54) (105,55)(106,55)(106,56)(107,56)(107,57)(108,57)(108,58)(109,58)(109,59) ... (182,59)(183,59)(183,55)(184,55)(184,50)(185,50)(185,55)(184,55)(184,59) (183,59)(183,61)(182,61)(182,63)(181,63)(181,65)(180,65)(180,66)(179,66) ... (108,58)(107,58)(107,57)(106,57)(106,56)(105,56)(105,55)(104,55)(104,54) (103,54)(103,53)(102,53)(102,52)(101,52)(101,51)(100,51)(100,50). >> Edge structure at line 13: %% reflectă structura asociată curbei 'firstq' row 80: 145+ 157- 150+ 150- 151+ 151- | row 79: 140+ 161- 157+ 145- | row 78: 137+ 164- 161+ 140- | ... ... row 51: 101+ 185- 184+ 102- | row 50: 100+ 185- 184+ 101- | )
Ne putem da seama că 'firstq' este cuprinsă între liniile ("row") 50 şi 80 ale ecranului; într-adevăr, fixasem axa $z_0z_1$ la 50 de pixeli distanţă faţă de marginea de sus, iar înălţimea celui mai de sus punct $z_2$ este $\small\mathsf F/2$=30 (deci $z_2$ se află pe linia 50+30=80); înregistrarea "row 50: 100+ 185- 184+ 101-" ne spune că pe linia 50 sunt marcaţi pixelii din coloanele 100 şi 184 (aceştia ar corespunde punctelor $z_0$ şi respectiv $z_1$).
Interpretând astfel înregistrările "row", am putea trasa chiar şi manual, arcul 'firstq'. Dar este mult mai uşor de folosit lista de puncte expusă drept conţinut al variabilei 'currentpicture'; copiem lista respectivă într-un fişier "picture.csv" şi aici, separăm punctele pe câte o linie, apoi ştergem toate parantezele (operaţii pentru care putem angaja diverse programe utilitare, de exemplu sed sau awk) şi adăugăm un "header", denumind cele două coloane:
x, y 101,50 101,51 102,51 ... 101,51 100,51 100,50
Acum putem folosi R, pentru a plota aceste puncte:
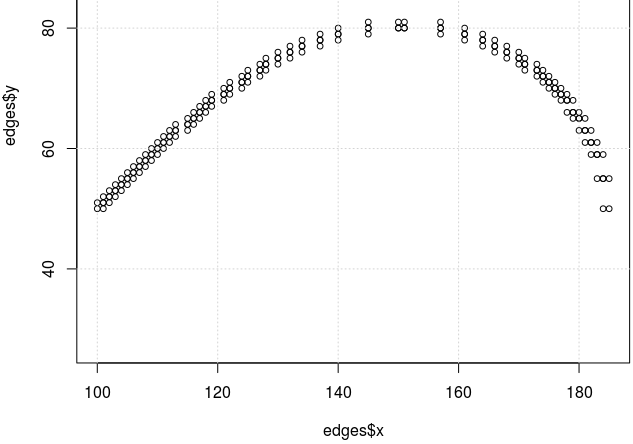
Privind de departe, am putea recunoaşte asemănarea cu o semibuclă $\mathcal{B}$ (ceea ce am şi putea verifica, plotând din R ecuaţiile corespunzătoare); de fapt "graficul" obţinut este cam ciudat… Printr-un "program de grafică" obişnuit (de exemplu, folosind R) am fi obţinut o serie de pixeli nestructuraţi în vreun fel special, ai arcului de curbă respectiv. Dar MF a fost creat nu pentru grafică, ci pentru a genera fonturi; "output"-ul său trebuie asociat de regulă unui set de caractere (MF şi informează la un anumit moment: "output written on... 1 character").
Vom vedea mai jos că MF a folosit aici modul implicit "proof", pentru care punctele curbei sunt reprezentate prin caractere dintr-un font special 'gray' - în fond, regiuni dreptunghiulare pe care sunt marcate anumite configuraţii simple de pixeli; iar pentru producerea structurilor "edge" dintre care am redat parţial mai sus, MF alege (cumva) caractere 'gray' potrivite învecinării punctelor pe direcţiile principale şi eventual, mai ajustează intern (elimină, adaugă sau comasează) pixelii care eventual se suprapun (scopul principal fiind acela de a atenua asperităţile datorate rotunjirii coordonatelor, vizibile mai ales în proximitatea direcţiilor verticale sau orizontale).
Este desigur instructiv (probabil că doar "instructiv") să angajăm astfel R, dar în mod standard vizualizarea dorită se obţine îmbinând alte instrumente (unele specifice sistemului TeX, altele proprii sistemului grafic general); intercalând înainte de end comanda shipit; şi relansând mf obţinem un fişier în formatul "Generic Font" (.gf), care poate fi convertit prin programul gftodvi în format DVI şi apoi poate fi vizualizat apelând de exemplu xdvi ("previewer"-ul obişnuit pentru fişierele DVI, în sistemul grafic X Window din Linux):
vb@Home:~/4_art/Latex/aVB/999$ mf firstquart This is METAFONT, Version 2.7182818 (TeX Live 2015/Debian) (preloaded base=mf) (firstquart.mf [0] ) Output written on firstquart.2602gf (1 character, 240 bytes) Transcript written on firstquart.log vb@Home:~/4_art/Latex/aVB/999$ gftodvi firstquart.2602gf vb@Home:~/4_art/Latex/aVB/999$ xdvi firstquart.dvi

Să observăm întâi, notiţa produsă de mf: "preloaded base=mf" (o notiţă similară avem şi când invocăm un compilator de TeX - de exemplu "preloaded format=latex"); aceasta denotă că pentru compilarea programului pe care i l-am indicat, MF (respectiv LaTeX, sau alt compilator de TeX) se va baza pe un anumit "pachet" de comenzi predefinite. Avem o metodă sigură, pentru a depista acest pachet: folosim opţiunea -recorder (lansând MF prin mf -recorder firstquart); va rezulta atunci un fişier "firstquart.fls", care indică fişierele citite sau scrise pe parcurs:
PWD /home/vb/4_art/Latex/aVB/999 % directorul de lucru curent INPUT /etc/texmf/web2c/texmf.cnf % configurează căile de căutare a fişierelor INPUT /usr/share/texmf/web2c/texmf.cnf INPUT /usr/share/texlive/texmf-dist/web2c/texmf.cnf INPUT /var/lib/texmf/web2c/metafont/mf.base % macro-urile de bază INPUT firstquart.mf OUTPUT firstquart.log OUTPUT firstquart.2602gf
"Pachetul" căutat este /var/.../mf.base (indicat pe a cincea linie); am putea probabil să-l deschidem în vreun editor de text - dar mai bine, să ţinem seama de cum procedează în mod standard sistemul TeX: toate compilatoarele sale (inclusiv MF) au nevoie să încarce numeroase fişiere ("pachete" de bază, fişiere de fonturi, etc.) şi de aceea, se foloseşte biblioteca kpathsea, special creată pentru rezolvarea eficientă a problemelor legate de căutare.
Dar pe sistemul meu, comanda încercată imediat 'kpsewhich mf.base' nu dă niciun rezultat; aşa că (evitând să adaug în vreun fişier de configurare şi calea de căutare necesară) am deschis totuşi fişierul respectiv şi am văzut imediat (pe primul rând necomentat) base_name="plain" - de unde am dedus "plain.mf" ca fişier care ar trebui de fapt, căutat; folosind apoi operatorul clasic de substituire din interpretorul bash ("backticks"), am încărcat în gedit fişierul respectiv:
vb@Home:~/4_art/Latex/aVB/999$ gedit `kpsewhich plain.mf`
Putem avea o sinteză a conţinutului fişierului plain.mf astfel obţinut, căutând succesiv (v. meniul "Find..." al editorului respectiv) cuvântul "message":
message "Preloading the plain base, version "&base_version&": preliminaries,"; message " basic constants and mathematical macros,"; message " macros for converting from device-independent units to pixels,"; ...
În secţiunea marcată prin message " macros and tables for various modes of operation,"; găsim definiţia pe baza căreia 'proof' devine "modul de ieşire" implicit:
def mode_setup = warningcheck:=0; if unknown mode: mode=proof; fi % dacă nu s-a explicitat 'mode', atunci =proof ... if unknown mag: mag=1; fi ... pixels_per_inch:=pixels_per_inch*mag; ... fix_units; % define the conversion factors, given pixels_per_inch ... warningcheck:=1; enddef; ... ... La sfârşitul fişierului 'plain.mf': mode_setup; % establish proof mode as the default
Comanda (sau macro-ul) mode_setup este lansată în execuţie la sfârşitul încărcării fişierului plain.mf, încât dacă nu s-a explicitat variabila mode, atunci 'proof' devine "modul de ieşire" (pentru imprimantă, sau ecran) în cadrul sesiunii de lucru curente cu MF; iar dacă se explicitează 'mode' (lansând MF de exemplu astfel: mf '\mode=ljfour; input firstquart'), atunci "modul de ieşire" va putea fi cel indicat ("ljfour"), presupunând că există undeva o definiţie a acestuia. Dar să observăm că programul propriu ("firstquart.mf") transmis lui MF va trebui el însuşi, să apeleze mode_setup (pentru a activa modul indicat, 'ljfour'), fiindcă 'plain.mf' este executat automat înainte de programul propriu şi atunci, dacă nu s-ar reapela 'mode_setup', variabila 'mode' ar rămâne cu valoarea implicită 'proof'.
În secţiunea indicată mai sus găsim deasemenea, definiţia pentru 'proof':
% proof mode: for initial design of characters mode_def proof = proofing:=2; % yes, we're making full proofs fontmaking:=0; % no, we're not making a font tracingtitles:=1; % yes, show titles online pixels_per_inch:=2601.72; % that's 36 pixels per pt blacker:=0; % no additional blackness fillin:=0; % no compensation for fillin o_correction:=1; % no reduction in overshoot enddef;
Putem să ne explicăm acum, extensia ".2602gf" prevăzută de MF pentru fişierele pe care le produce; în macro-ul fix_units invocat cum se vede mai sus, în cursul subrutinei mode_setup, găsim între altele aceste valori:
pt:=pixels_per_inch/72.27; % "punct tipografic" in:=pixels_per_inch; % inch (1 in = 2.54 cm) hppp:=pt; % horizontal pixels per point
Aceasta înseamnă că 1in = 72.27pt şi dacă un "punct tipografic" ar măsura 36 de "pixeli", atunci rezoluţia grafică ar fi 72.27*36=2601.72≈2602 "pixels_per_inch" (sau "dots per inch"). Pentru un alt exemplu: modul 'ljfour' este prevăzut pentru imprimante Laser Jet cu rezoluţia de 600 dpi ("dots per inch"); atunci, un punct tipografic ar măsura 600/72.27 = 8.3022≈8 pixeli.
Mai avem de observat introducerea unor unităţi de măsură abstracte, precum pt# := 1 şi in# := 72.27; comanda define_pixels le va transforma în unităţi "obişnuite" (dependente de rezoluţia modului de ieşire). Am avea astfel o manieră comodă de parametrizare: fixăm din start o unitate de măsură (abstractă), să zicem U# := 4/9pt#; apelăm apoi define_pixels(U) şi exprimăm toate coordonatele folosind U; coordonatele "reale" (în pixeli) ale oricărui punct vor depinde atunci de rezoluţia modului de ieşire (de exemplu, pentru modul 'proof' avem 1pt = 36 pixeli, deci U = 16, încât în acest caz punctul z1=(10U, 5U) va avea coordonatele în pixeli (160, 80)).
După revederile şi explorările întreprinse mai sus, vom putea probabil (în "partea a patra") să definitivăm lucrul pe care ni l-am propus: să creem (în mod onorabil) un font (pentru LaTeX) conţinând două simboluri pentru "cerc prin origine" şi două simboluri pentru lemniscatele Bernoulli care corespund acestor cercuri.
vezi Cărţile mele (de programare)