Mofturile repartizării lecţiilor
[1] De capul meu prin problema orarului şcolar (pe Google Play)
Experimentăm iarăşi programele dezvoltate în [1], căutând un orar echilibrat pentru datele de încadrare a profesorilor din orarul vizat în [3]. Dar nu condiţionăm folosirea sălilor şi preferând desfăşurarea lecţiilor într-un singur schimb, se pare că avem mari şanse de a descoperi (eventual) fel de fel de hibe şi îmbunătăţiri ale programelor respective (fiind numere mari de clase, profesori şi cuplaje).
O abordare lejeră
Am demarat tranşant (fără a bănui la „hibe şi îmbunătăţiri”): prin funcţia mount_days() (v. [1]) am obţinut (în doar 2-3 min.) o repartizare „cvasi-omogenă” a lecţiilor pe zile; am şi ajustat-o interactiv, prin Recast.html (dar cam la repezeală) – echilibrând numărul de ore pe fiecare zi şi omogenizând încă vreo câteva distribuţii individuale; apoi, prin mount_hours() am obţinut (iarăşi, foarte repede) „orarele” pe fiecare zi (cu ghilimele, fiindcă pentru a decurge rapid, mount_hours() neglijează anumite cerinţe asupra lecţiilor cuplate).
Mai rămânea de aplicat pe fiecare zi, programul de eliminare a suprapunerilor ascunse induse de cuplaje şi apoi, pe cel de reducere a numărului de ferestre…
Dar acum lucrurile au început să devină interesante, pentru că funcţia correct() a cam eşuat – în sensul că rezultatul produs este greşit, cum arată acest extras din „orarul” pe clase al uneia dintre zile:
1 2 3 4 5 6 7
12C ex2N01 Bi2 M02 Ef2 N01 Re1 -
11D Ef4 N07N01 N01 Ch1 R08 - -
12I Bi3 N11N01 M10 Fz6 R03 N01 -
10D Ti1 M10 Ps1 Fz1 Le3 N09N01 -
În ziua respectivă N01 are 3 ore proprii şi este angajat în 4 cuplaje; correct() n-a reuşit să elimine suprapunerea din ora 2 (când N01 ar trebui să intre cu N07 la clasa 11D şi cu N11 la 12I) şi a rămas să o corectăm interactiv – numai că aceasta este imposibil: toate cele 4 clase implicate au câte 6 (sau numai 5) ore, încât cele 7 lecţii ale lui N01 chiar nu pot fi efectuate corect (fără suprapunere cu o altă lecţie).
Totuşi… situaţia ar putea fi „corectată” uşor, admiţând ca o clasă (de exemplu 12I) să înceapă programul de la a doua oră a zilei (încât să putem muta N11N01 în a 7-a oră). Şi chiar aşa stau lucrurile pe orarul original: unele clase încep programul nu de la prima oră (cum ar fi normal), ci de la a doua (sau chiar, de la a treia) oră a zilei (v. [3]).
Dar nici nu ne gândim, să „îmbunătăţim” funcţia correct() (făcând-o să permită începerea programului de la ora 2)… Necesitatea unor derogări decurge tocmai de la proiectarea iniţială (cam defectuoasă, ori neprincipială) a încadrării: sunt cam multe cuplaje şi în orice caz, prea multe cuplaje care-l angajează pe N01.
Să nu modelăm derogări! La urma urmei, un pachet de programe are de reflectat consecvent principiile domeniului pe care vrea să-l deservească, nu obişnuitele chichiţe şi ascunzişuri legislative înşurubate tam-nisam din exteriorul acestuia.
Avem de constatat doar că ne-am grăbit, neglijând poate faptul că distanţarea temporală deja mare, faţă de [1], a indus în mod firesc o anumită estompare a demersurilor necesare; s-o luăm deci de la capăt, mai „aşezat”.
Repartizarea lecţiilor pe zilele săptămânii
Mai întâi am constituit un set de date TwCl în care am convenit deja o repartizare prof | cls | zl pentru lecţiile cărora li se impune împerecherea anumitor clase, în anumite zile (e vorba de ceea ce numisem anterior „cuplaje de clase”, sau cumva peiorativ "twins"):
> str(TwCl) 'data.frame': 18 obs. of 3 variables: $ prof: chr "Ev1" "Ev1" "Ev1" "Ev1" ... $ cls : Factor w/ 42 levels "10A","10B","10C",..: 1 2 3 4 5 6 7 8 9 34 ... $ zl : int 1 2 3 4 5 1 2 3 4 1 ...
În cazul de faţă am împerecheat în fiecare zi câte o clasă de-a 9-a şi una de-a 10-a; profesorii Em1 şi Ev1 vor trebui să intre simultan, respectiv la a 9-a şi la a 10-a, sau invers – după cum săptămâna în curs este de rang par sau impar (acest aranjament satisface norma de „jumătate de oră” pe săptămână, alocată – cam după ureche, dar „de sus” – pentru disciplinele "Educaţie muzicală" şi "Educaţie vizuală").
În lessons.RDS avem lecţiile prof | cls care au mai rămas de repartizat pe zile:
LSS <- readRDS("lessons.RDS") 'data.frame': 1242 obs. of 2 variables: # fără lecţiile din TwCl $ prof: Ord.factor w/ 108 levels "N02"<"N02N12"<..: 1 1 1 1 1 1 1 1 1 1 ... $ cls : Factor w/ 42 levels "10A","10B","10C",..: 28 28 37 15 15 15 15 17 17 17 ...
Generăm prin mount_days() măcar vreo 10 distribuţii pe zile (timpul mediu unitar este în jurul a 3 minute) şi alegem una care să aibă cât mai puţine situaţii în care un profesor angajat în cuplaje cumulează 7 ore şi care să fie cât mai echilibrată faţă de totalul orelor pe fiecare zi.
DS <- readRDS("byDays/L9.RDS") # o distribuţie pe zile, prof|cls|zl 'data.frame': 1260 obs. of 3 variables: $ prof: Ord.factor w/ 108 levels "N02"<"N02N12"<..: 95 99 99 99 38 67 67 67 33 33 ... $ cls : Factor w/ 42 levels "10A","10B","10C",..: 1 1 1 1 1 1 1 1 1 1 ... $ zl : Factor w/ 5 levels "Lu","Ma","Mi",..: 4 5 2 3 1 4 5 2 3 1 ...
mount_days() a adăugat în final şi repartiţia celor 18 lecţii, convenită iniţial în TwCl.
Ne interesează distribuţiile individuale, rezultate pentru profesori; n-am vrea ca diferenţa dintre numărul total de ore pe o zi şi alta să fie mai mare de 1, n-am vrea ca profesorul să aibă mai mult de 6 ore pe zi şi în general – am vrea distribuţii uniforme.
Investigăm caracteristicile respective prin funcţii prevăzute deja în [1]:
iDS <- dis_indiv(DS) > head(iDS, 3); iDS[iDS$prof=="N01", ] prof Lu Ma Mi Jo Vi Sum 1 Sum 254 250 254 252 250 1260 # Totaluri 2 Ge1 5 5 5 5 5 25 # distribuţie uniformă 3 R01 5 4 5 4 6 24 # distribuţie aproape uniformă 1 N01 3 3 3 5 3 17 # ore proprii (nu în cuplaj) > total_conn(iDS) # pentru cei angajaţi în cuplaje, care au şi ore proprii prof Lu Ma Mi Jo Vi 1 N02 5 4 4 6 6 prof Lu Ma Mi Jo Vi 2 N12 2 3 3 5 3 11 N13 2 3 0 4 4 3 N03 6 6 6 6 5 12 N11 2 3 4 5 2 4 N10 5 2 3 3 2 13 N04 2 5 6 5 3 5 N06 5 6 3 5 2 14 N08 3 1 2 2 3 6 N05 3 3 4 3 3 15 Le4 6 3 4 5 5 7 N09 4 3 4 2 3 16 Le2 6 6 5 6 6 8 N14 2 3 2 1 1 17 Lg3 2 1 1 1 1 9 N01 5 7 7 6 7 18 Lg1 6 5 4 4 5 10 N07 3 6 4 4 3 19 Lg2 2 2 2 3 2
În distribuţia pe care am ales-o, totalul zilnic de ore diferă de la o zi la alta cu cel mult 4 ore; pentru echilibrare va trebui să schimbăm unele valori $zl (înlocuind unor lecţii, "Lu" sau "Mi" alocate iniţial, cu "Ma" sau "Vi" de exemplu). Analog, mutând o clasă dintr-o zi în alta la un profesor, putem omogeniza distribuţia iniţială a orelor acestuia (sau dimpotrivă – o putem condensa în mai puţine zile).
Dar devine foarte important ce clase şi profesori, mutăm dintr-o zi în alta – pentru că numărul de ore pe zi la clase variază (între 5 şi 7), pentru că sunt multe cuplaje şi pentru că un acelaşi profesor este implicat în mai multe (prea multe) cuplaje.
Profesorul N01 (cel care pe disciplina principală "Informatica" are cel mai multe ore, v. [2]) are 17 ore proprii şi 15 ore în cuplaj cu alţii – astfel că trebuie exceptat de la regula asumată de mount_days(), după care profesorul are cel mult 6 ore pe zi. Dar în DS au rezultat trei zile în care N01 cumulează câte 7 ore şi de fapt, ar fi necesare numai două zile; fireşte că vom muta în ziua "Lu" (când cumulează numai 5 ore), una sau alta dintre lecţiile (proprii sau în cuplaj) din zilele cu 7 ore ale sale.
Funcţia toRecast() (v. [1]) reformulează distribuţia DS pentru a evidenţia clasele repartizate în fiecare zi profesorilor; vom putea muta clase dintr-o zi în alta folosind aplicaţia interactivă Recast.html, sau folosind direct din consolă vreo două funcţii uşor de imaginat (prin care să investigăm anumite subseturi, sau să mutăm clase):
RC <- toRecast(DS) write_csv(RC, file = "DS.csv") # pentru aplicaţia interactivă "Recast.html" joint_dis <- function(P) RC %>% filter(prof %in% c(P, Tw1[[P]])) print(joint_dis("N01")) # distribuţiile care angajează pe N01 prof Lu Ma Mi Jo Vi 1 N09N01 10D 10D 10D 2 ex3N01 10I 10I 10I 3 N01 11D 12D 12I 11D 12C 12I 12C 12D 12I 10I 11D 12C 12D 12I 11D 12C 12D 4 N07N01 11D 11D 11D 5 ex2N01 12C 12C 12C 6 N11N01 12I 12I 12I
Amintim că Tw1 şi Tw2 sunt „dicţionare” stabilite în prealabil pentru datele de încadrare şi evidenţiază de care alţi profesori depinde alocarea pe zile şi ore a lecţiilor unui profesor care este angajat în unul sau mai multe cuplaje; de exemplu Tw1[["N01"]] indică acele cuplaje ("N09N01", "ex3N01" etc.) care îl angajează pe N01.
Ne punem la dispoziţie şi o funcţie prin care să putem schimba o valoare $zl din distribuţia iniţială DS (asigurând „mutarea” unei lecţii din ziua în care a fost repartizată iniţial prin DS, într-o altă zi):
change_zl <- function(P, Q, Z, Nzl) DS[with(DS, prof==P & cls==Q & zl==Z), "zl"] <<- Nzl
De exemplu, prin change_zl("N07N01", "11D", "Vi", "Lu") am obţine pentru N01 distribuţia echilibrată (6, 7, 7, 6, 6), în locul celei iniţiale (5, 7, 7, 6, 7); doar că este necesar să verificăm dacă mutarea respectivă nu „strică” prea tare, distribuţia orelor lui N07 (care este şi el, parte din mai multe cuplaje) şi mai trebuie eventual, să vedem (mai târziu) cum „reparăm” distribuţia pe zile a orelor clasei mutate…
La prima vedere pare complicat să omogenizăm distribuţiile individuale; ar fi tare greu de formulat un program prin care să „automatizăm” lucrurile, iar operând prin interfaţa interactivă Recast.html – cum procedam anterior – este sâcâitor şi devine complicat din cauză că avem multe cuplaje.
Însă funcţiile simple pe care ni le-am pus la dispoziţie mai sus, ne asigură o procedură de lucru unitară, prin care putem retuşa uşor oricare distribuţie individuală; o descriem aici pentru cazul celor angajaţi în cuplaje: după ce facem o mutare prin change_zl(), afişăm prin dis_indiv() distribuţiile rezultate, decidem (pe rând) la cine să retuşăm distribuţia curentă, folosim apoi toReast() şi joint_dis() pentru a vedea ce clasă ar fi mai convenabil să mutăm şi facem mutarea aleasă (sau mutările, dacă decidem să mutăm două clase) folosind change_zl():
> change_zl("N07N01", "11D", "Vi", "Lu") > as.data.frame(total_conn(dis_indiv(DS))) # distribuţiile celor din cuplaje prof Lu Ma Mi Jo Vi 1 N02 5 4 4 6 6 prof Lu Ma Mi Jo Vi 2 N12 2 3 3 5 3 11 N13 2 3 0 4 4 3 N03 6 6 6 6 5 12 N11 2 3 4 5 2 4 N10 5 2 3 3 2 13 N04 2 5 6 5 3 5 N06 5 6 3 5 2 14 N08 3 1 2 2 3 6 N05 3 3 4 3 3 15 Le4 6 3 4 5 5 7 N09 4 3 4 2 3 16 Le2 6 6 5 6 6 8 N14 2 3 2 1 1 17 Lg3 2 1 1 1 1 9 N01 6 7 7 6 6 18 Lg1 6 5 4 4 5 10 N07 4 6 4 4 2 19 Lg2 2 2 2 3 2 > RC <- toRecast(DS) # recalculează RC, pentru a folosi joint_dis() > joint_dis("N07") # distribuţiile în care apare N07 prof Lu Ma Mi Jo Vi 1 N07 11A 10E 11A 9B 10E 11A 11A 9B # a muta 2 ore din Ma în Vi 2 N07N13 10E 10E 10E 3 N07N01 11D 11D 11D 4 N07N08 11G 11G 11G 5 N07N04 9C 9C 9C > change_zl("N07", "10E", "Ma", "Vi") > change_zl("N07", "11A", "Ma", "Vi")
După secvenţa de comenzi redată mai sus, N07 are o distribuţie omogenă a orelor: câte 4 ore în fiecare zi, singur sau în cuplaj (mai mult, de data aceasta: chiar şi clasele la care intră în cuplaj, nu apar de două ori într-o aceeaşi zi).
Repetând pentru ceilalţi profesori, procedura de lucru exemplificată mai sus (în total n-ar trebui să ia mai mult de 20 minute) – am obţinut distribuţii omogene pentru toţi profesorii care pe lângă ore proprii, au şi ore în cuplaje:
prof Lu Ma Mi Jo Vi
1 N02 5 5 5 5 5 prof Lu Ma Mi Jo Vi
2 N12 3 3 3 4 3 11 N13 2 3 2 3 3
3 N03 5 6 6 6 6 12 N11 3 3 3 4 3
4 N10 3 3 3 3 3 13 N04 4 5 4 4 4
5 N06 5 4 4 4 4 14 N08 2 2 2 2 3
6 N05 3 3 4 3 3 15 Le4 5 4 4 5 5
7 N09 4 3 3 3 3 16 Le2 6 6 5 6 6
8 N14 2 2 2 2 1 17 Lg3 2 1 1 1 1
9 N01 6 7 6 7 6 18 Lg1 6 5 4 4 5 # distribuţie rămasă "cvasi-omogenă"
10 N07 4 4 4 4 4 19 Lg2 2 2 2 3 2
Dacă vrem, putem aplica joint_dis() tuturor cheilor din Tw1, obţinând distribuţia tuturor lecţiilor acestor profesori:
> RC <- toRecast(DS) > map_dfr(names(Tw1), joint_dis) %>% distinct() prof Lu Ma Mi Jo Vi 1 N02 11F 11H 11F 11H 5A 7A 11F 11H 7A 9D 11F 7A 8B 11H 5A 8A 2 N02N12 11C 12D 9D 12D 11C 12D 9D 11C 9D 3 N03N12 10H 10H 10H 4 N12 11C 11C 11C 11C 5 N03ex1 11I 9H 9E 9H 11I 11I 9E 9E 9H 6 N03 11I 9E 9H 10H 11I 10H 9E 9H 10B 11I 9H 10B 11I 9E 7 N10N03 11H 11H 11H 8 N10N06 10F 9F 9F 10F 9F 10F 9 N10 12B 12B 9F 10F 12B 12B 10 N06 12H 9F 10F 12H 10G 12H 12H 10G 9F 11 N06ex2 12H 12E 12H 12H 12E 12E 12 N05 9A 12G 9G 12G 9A 9G 12G 9G 12G 9A 13 N05ex2 9G 9G 9G 14 N11N05 12G 12G 12G 15 N09N14 12F 12F 9I 12F 9I 9I 16 N09 10C 12F 10D 12F 12F 10C 12F 17 N09N01 10D 10D 10D 18 N14 9I 9I 9I 19 ex3N01 10I 10I 10I 20 N01 11D 12D 12I 11D 12C 12I 12C 12D 12I 10I 11D 12C 12D 12I 11D 12C 12D 21 N07N01 11D 11D 11D 22 ex2N01 12C 12C 12C 23 N11N01 12I 12I 12I 24 N07 11A 9B 10E 11A 11A 10E 11A 9B 25 N07N13 10E 10E 10E 26 N07N08 11G 11G 11G 27 N07N04 9C 9C 9C 28 N13 6A 6A 6B 6B 29 N13N04 11B 9B 11B 9B 11B 9B 30 N11ex3 10G 10G 10G 31 N11 11E 11E 11E 11E 32 N11ex2 11E 11E 11E 33 N04 10A 11B 9B 9C 11B 12A 10A 11B 12A 12A 11B 12A 34 N08 12E 11G 12E 11G 12E 11G 11G 12E 35 Le4 11A 11C 8B 10E 12A 9D 12A 7A 9D 11A 7A 8B 10E 11C 8B 36 Le4Le2 10B 12B 10B 12B 10B 12B 10B 12B 37 Le2 12I 5A 8A 9C 10F 5A 6A 6B 9I 5A 6A 8A 9I 10F 11B 12I 6B 11B 5A 6B 9C 38 Lg3Lg1 10A 10A 10A 10A 10A 39 Lg3 10A 40 Lg2Lg1 11A 9A 11A 9A 11A 9A 11A 9A 11A 9A 41 ex4Lg1 12A 12A 12A 12A 12A 42 Lg1 12A 8A 11A 8A 43 Lg2 9A
Cum se întâmplă adesea, observăm la sfârşit că a rămas totuşi o distribuţie care nu este omogenă – cea a orelor lui Lg1; dar pe tabelul redat mai sus (v. linia 42) vedem imediat că mutarea change_zl("Lg1", "8A", "Lu", "Mi") omogenizează şi această distribuţie (ţinând cont şi de cuplajele lui Lg1).
Desigur, se cuvine să reţinem distribuţia DS (a tuturor lecţiilor) rezultată:
> saveRDS(DS, file="distr.RDS") > write_csv(RC, file="distr.CSV") # eventual, pentru "Recast.html"
Dar se cuvine să mai observăm că mutarea de clasă dintr-o zi în alta, practicată mai sus, s-a făcut fără a controla numărul zilnic de ore ale acelei clase – încât au apărut situaţii în care o clasă are într-o zi 8 ore şi în alta 5 (sau şi mai rău):
> table(DS[c("cls", "zl")]) cls Lu Ma Mi Jo Vi cls Lu Ma Mi Jo Vi cls Lu Ma Mi Jo Vi 10A 7 6 6 7 6 11F 6 6 6 6 5 6A 5 6 7 6 5 10B 5 7 6 6 6 11G 5 7 6 5 6 6B 6 6 7 5 6 10C 6 5 7 5 5 11H 5 6 6 6 6 7A 6 7 7 6 6 10D 6 6 5 8 6 11I 6 5 6 6 6 8A 5 6 7 7 7 10E 5 6 6 6 8 12A 6 6 6 5 6 8B 6 6 7 7 6 10F 7 6 6 6 6 12B 6 5 6 6 5 9A 7 7 6 6 6 10G 7 6 6 4 8 12C 5 6 6 6 6 9B 7 7 5 6 6 10H 6 6 7 6 6 12D 6 5 6 6 6 9C 7 6 6 6 6 10I 6 6 6 7 6 12E 6 5 6 6 6 9D 6 6 7 7 5 11A 6 5 6 6 6 12F 6 6 6 5 6 9E 6 6 6 6 7 11B 6 6 5 5 7 12G 6 6 5 6 6 9F 6 6 6 6 7 11C 7 5 6 5 6 12H 6 6 6 5 6 9G 6 7 6 6 6 11D 7 6 5 6 5 12I 6 6 6 5 6 9H 6 6 7 6 6 11E 6 5 6 6 6 5A 6 6 5 5 6 9I 6 5 6 8 6
Ca să retuşăm distribuţia pe zile a orelor unei clase, avem iarăşi de mutat lecţii dintr-o zi în alta – dar desigur, la profesori neangajaţi în cuplaje, pentru a nu „strica” repartizarea obţinută mai sus a orelor acestora.
Am putea imagina o procedură de lucru analogă celeia folosite mai sus pentru cuplaje: afişăm repartizarea curentă a lecţiilor clasei, alegem lecţia pe care s-o mutăm, apoi folosim change_zl(). Dar această procedură este oferită deja de "Recast.html" – care permite selectarea lecţiilor pe o clasă sau alta şi mutarea lecţiei alese într-o altă zi (specificând şi totalurile zilnice rezultate şi asigurând în plus, exportarea în orice moment a distribuţiei curente); câtă vreme nu ne mai atingem de cuplaje, va fi mai simplu de lucrat în Recast.html, decât în consola R.
Copiem deci conţinutul fişierului "distr.CSV" în elementul <textarea> din Recast.html şi deschizând în browser (Firefox), selectăm clasa 10B (prin "Mark") – cu intenţia de a omogeniza distribuţia iniţială (5 7 6 6 6) a orelor acesteia:
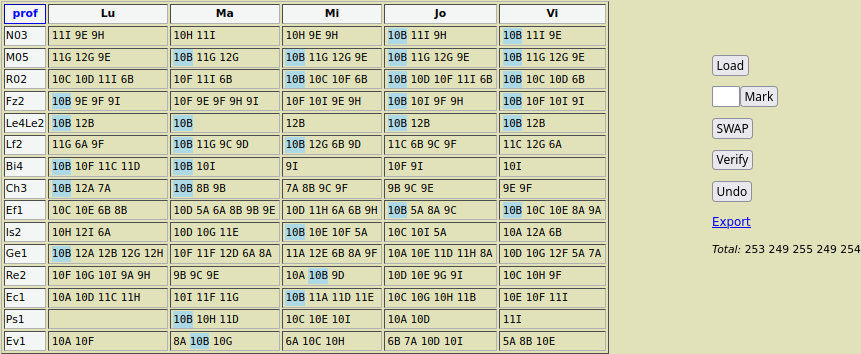
Trebuie să mutăm un "10B" din ziua Ma, în ziua Lu, unuia dintre cei neangajaţi în cuplaje; deocamdată alegem mutarea fără a ne gândi şi la omogenizarea vreuneia dintre distribuţiile individuale. Excludem Ev1, nevrând să stricăm împerecherea de clase a 10-a şi a 9-a instituită prin TwCl la profesorii Ev1 şi Em1; preferăm să mutăm pe linia lui Ps1 (care nu apare în vreun cuplaj): pe linia respectivă, bifăm prin click 10B şi apoi, câmpul din ziua destinaţie Lu şi încheiem mutarea folosind butonul "SWAP" (urmarea fiind că acum, 10B are în fiecare zi câte 6 ore).
Procedăm la fel, pentru fiecare clasă pentru care distribuţia orelor din tabelul redat mai sus este neuniformă; după toate aceste operaţii (care n-au de ce să ia mai mult de vreo 10-15 minute, în total) – folosim butonul "Export", obţinând fişierul "re-distr.csv" corespunzător modificărilor efectuate asupra distribuţiei iniţiale.
Folosind fromRecast() (v. [1]), recuperăm în consola R distribuţia modificată şi tabelăm iarăşi distribuţiile pe zile ale orelor claselor:
> DS <- read_csv("re_distr.csv", col_types="cccccc") %>% fromRecast() > addmargins(table(DS[c('cls', 'zl')])) 10A 7 6 6 7 6 11G 5 6 6 6 6 6B 6 6 6 6 6 10B 6 6 6 6 6 11H 5 6 6 6 6 7A 6 7 7 6 6 10C 6 5 6 5 6 11I 6 5 6 6 6 8A 6 6 7 6 7 10D 6 6 6 7 6 12A 6 6 6 5 6 8B 6 6 7 7 6 10E 6 6 6 6 7 12B 6 5 6 6 5 9A 7 7 6 6 6 10F 7 6 6 6 6 12C 5 6 6 6 6 9B 7 6 6 6 6 10G 7 6 6 6 6 12D 6 5 6 6 6 9C 7 6 6 6 6 10H 6 6 7 6 6 12E 6 5 6 6 6 9D 6 6 6 7 6 10I 6 6 6 7 6 12F 6 6 6 5 6 9E 6 6 6 6 7 11A 6 5 6 6 6 12G 6 6 5 6 6 9F 6 6 6 6 7 11B 6 6 5 6 6 12H 6 6 6 5 6 9G 6 7 6 6 6 11C 6 6 6 5 6 12I 6 6 6 5 6 9H 6 6 7 6 6 11D 6 6 6 6 5 5A 6 6 5 5 6 9I 6 6 6 7 6 11E 6 5 6 6 6 6A 6 6 6 6 5 11F 6 6 6 6 5 Lu Ma Mi Jo Vi Sum 255 248 254 251 252
Constatăm că acum, toate clasele au distribuţii orare uniforme (numărul de ore pe clasă diferă cu cel mult 1, de la o zi la alta). S-ar cuveni să echilibrăm şi sumele „verticale”: alegând pe baza tabelului redat mai sus, câte o clasă la care să schimbăm ziua în care are 7 ore (sau în care are 6 ore, pentru clase cu mai puţin de 30 de ore) – ajungem uşor (iarăşi prin "Recast.html") la o distribuţie în care pe fiecare zi avem câte 252 de ore.
Desigur, am ales astfel profesorul căruia să-i mutăm clasa într-o altă zi, încât să păstrăm regula de a nu avea două ore la clasa respectivă, în noua zi alocată.
A rezultat până aici, o distribuţie care este echilibrată pe cuplaje, pe clase şi pe totaluri; pentru a o definitiva, trebuie să vedem profesorii neangajaţi în cuplaje la care distribuţia orelor este încă neomogenă – şi fie să o uniformizăm, dacă profesorul respectiv are suficient de multe ore, fie să o condensăm în cât mai puţine zile, dacă are puţine ore pe săptămână.
De data aceasta însă, mutarea de clasă dintr-o zi în alta trebuie condusă bilateral: mutarea unei clase din ziua z1 în ziua z2 la un profesor trebuie urmată imediat cu mutarea aceleiaşi clase din ziua z2 în ziua z1 la un alt profesor – încât să nu stricăm echilibrele tocmai constituite mai sus.
Este convenabil să lucrăm tot pe clase, cum am procedat şi mai sus; de exemplu, selectând prin "Mark" liniile clasei 9G, observăm că putem uniformiza distribuţia orelor lui M04 şi totodată, putem condensa pe cea a lui R09 – mutând 9G din ziua Mi în ziua Lu lui M04 şi invers, lui R09:
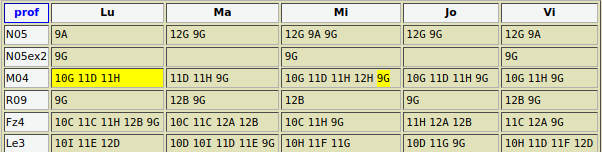
Fiindcă R09 are 4 ore la 9G – refuzăm în principiu (în toate cazurile similare acestuia), să-i condensăm distribuţia orelor în mai puţin de 4 zile.
De data aceasta – lucrând totuşi relaxat, în Recast.html – ne-a luat peste o oră, pentru a uniformiza (sau după caz, a condensa) distribuţiile individuale pentru toţi profesorii care nu-s angajaţi în cuplaje; după exportarea finală şi recuperare:
> DS <- read_csv("re_distr.csv", col_types="cccccc") %>% fromRecast()
avem în DS o distribuţie pe zilele de lucru a tuturor lecţiilor, care este omogenă faţă de zile (pe fiecare zi sunt câte 252 de ore), clase (pentru fiecare clasă, numărul zilnic de ore diferă cu cel mult 1, de la o zi la alta), profesori (orele fiecăruia sunt distribuite uniform pe zile, exceptând cazuri când numărul de ore este mic) şi discipline (de regulă, în oricare zi fiecare disciplină apare la clasă cel mult o singură dată). În plus să zicem, numărul de lecţii cuplate are diferenţe mici, de la o zi la alta.
Redăm distribuţia DS finală, în format CSV – începând cu profesorii neangajaţi în cuplaje şi adăugând mai la sfârşit (cu unele intercalări) pe cei cu lecţii cuplate (la care avem o singură modificare, faţă de setul de 43 de linii redat prin joint_dis() mai sus: la Lg3 am mutat 10A din ziua Lu, în ziua Vi); desigur, am colorat distinct pe zile (trecând fişierul ".csv" printr-un program AWK, ca şi în [1]), facilitând observarea caracteristicilor distribuţiilor individuale:
prof,Lu,Ma,Mi,Jo,Vi M07,5A 6B 9A,5A 6B 9A 9F,5A 6B 9F,5A 6B 9A 9F,5A 6B 9A 9F M08,12D 9D 10H,10H 11E 9D,10H 11E 12D,10H 11E 9D 12D,11E 12D 9D M05,11G 12G 9E,10B 11G 12G,10B 11G 12G 9E,10B 11G 12G 9E,10B 11G 12G 9E M04,10G 11D 11H 9G,11D 11H 9G,10G 11D 11H 12H,10G 11D 11H 9G,10G 11H 9G M01,10I 12H 9H 9I,11I 12H 9H 9I,10I 11I 12H 9I,10I 11I 9H 9I,10I 11I 12H 9H M06,11E 12A 9B 12B,10A 10C 12A,10A 10C 12A 9B,10A 10C 12A 9B,10A 10C 9B M10,10D 12I 9C,10D 11B 12I 9C,10D 11B 12I,10D 9C 11B,11B 12I 9C M02,10E 12C 6A 7A,12C 6A 7A,10E 12C 6A 7A,10E 12C 6A 7A,12C 6A 7A 10E M09,11B 11F 12F 10F,11F 12F 12I,10F 11F 12F,10F 11F 12F,11F 12F 10F M03,11A 11C 12B 12E,11A 11C 12B 12E,11A 11C 12B 12E,11C 12B 12E,11C 12E 11A M11,8A 8B,8A 8B,8A 8B,8A 8B,8A 8B R03,12I 5A 8B 9A,5A 8B 9A 7A,5A 7A 8B 9A,5A 7A 8B 12I,12I 7A 8B 9A R01,11B 11E 9C 9D 10E,10E 11C 11E 9D 12D,10E 11C 12D 9C 9D,11B 11C 12D 9C,11B 11E 12D 9C 9D R05,10G 10I 9B,10G 10I 9H 9E,9B 9E 9H 10G,9B 9E 9H,10I 9B 9E 9H R06,6A 8A 9F,12E 6A 8A 9F,6A 8A 9F,12E 6A 8A 9F,12E 6A 8A R09,,12B 9G,12B 9G,9G,12B 9G R10,9I,,9I,9I,9I R04,11F 12C 12F,10A 12F 12G,10A 12C 12F 11G,11F 11G 12C 12G,10A 11F 11G 12G R02,10C 10D 11I 6B,10F 11I 6B 10B,10B 10C 10F 6B,10D 10F 11I 6B,10B 10C 10D 6B R08,,10H 11D 12A,,10H 11D 12A,12A 10H 11D R07,11A 12H,11H 12H,,11A 11H,11A 11H 12H Fz1,10D 7A 9D 8A,10H 11B 7A 8A,10D 11B 12D 6B,10H 11B 12D 9D,10D 12D 9D 10H 6B Fz2,10B 9E 9F 9I,10F 9E 9F 9H 9I,10F 10I 9E 9H,10B 10I 9F 9H,10B 10F 10I 9I Fz4,10C 11C 11H 9G,10C 11C 12A 12B,10C 9G 12B,11H 12A 12B,11C 12A 9G 11H Fz5,10E 12C 9C,10A 12E 6A,12C 6A 9C,10A 10E 12C 12E,10A 10E 12E 9C Fz7,10G 11A,,,11A 10G,10G 11A Fz3,11G 12F 12G 11D,11F 11G 12G,11D 11F 12F 12H,11D 12G 12H,11F 11G 12F 12H Fz6,11E 12I 9B,11E 9A,9A 9B,12I 9A 9B,11E 12I Fz8,11I,,11I 8B,11I 8B, Le2,12I 5A 8A 9C,10F 5A 6A 6B 9I,5A 6A 8A 9I,10F 11B 12I 6B,11B 5A 6B 9C Le4,11A 11C 8B,10E 12A 9D,12A 7A 9D,11A 7A 8B,10E 11C 8B Le1,10A 10C 12E 12F 12H,12C 12H 9E 9F,10C 11I 12G 9H 11H,10A 11H 12E 9E 9H,11I 12C 12F 12G 9F Le3,10I 11E 12D,10D 11D 11E 9G,10H 11F 11G 10I,10D 11G 9G,10H 11D 11F 12D Le4Le2,10B 12B,10B,12B,10B 12B,10B 12B Le5,9B 10G,10G 9A,9A 9B,, Lf1,10G 12E 5A 9B,10E 11B 12C 12D,10E 11B 11E 12E,11E 12D 8B 10G,12C 5A 8B 9B Lf2,11G 6A 9F 9D,10B 11G 9C 9D,10B 12G 6B,11C 6B 9C 9F,11C 12G 6A Lf3,10F 9E 11H,12F 12I 9H,11D 12I 9E 9G,10F 11H 12F,11D 9G 9H Lf4,11I 7A,10C 10D 12H,11I 10D 9I,10C 9I,12H 7A Lf5,10H 10I 11F,,12B 7A 10H,10I 11F 12B, Bi3,6B 7A 11B,10E 6B 7A,5A 8A 8B 12E,10E 6A 9D,12I 6A 9D Bi1,10D 9C 9H 12G,10A 11I 9E 9F,10A 11E 9B 9E 12F,12H 9A 9B 9F,10D 9A 9C 9H Bi2,10C 10H 12A 12B,11H 9G 12D,10C 10G 9G,10G 12C 11G,10H 11A 11F Bi4,10B 10F 11D,10I 11C,,10F 9I 10B,10I 9I Ch4,10E 12D 8A,9D 11B 10E,10D 12E 9D,8A 11E,10D 12I Ch3,10B 12A 7A,10B 8B 9B,8B 9C 9F,9B 9C 9E 7A,9E 9F Ch1,10I 9A 9G,11C 11I 9H 9I,9A 9H 9I,10I 12C 11A,11D 12B 9G Ch2,10H 11F 11H,10C 12G 10A,10F 10G 11G,10A 10C 10G 10H,10F 12H 12F Ef1,10C 10E 6B 8B 9E,10D 5A 6A 8B 9B,10D 11H 6A 9H,10B 5A 8A 9C 6B,10B 10C 10E 8A 9A Ef2,12C 12G 12D 9D,11A 12F 7A,10H 11C 12A 12I,12E 12H 7A,10H 11B 12B 11E Ef4,11I 9G 11F,,9F 11D,,11G 9I Ef3,10F 10A,10A 10G,10G 10I,,10F 10I Is2,10H 12I 6A,10D 10G 11E,10B 10E 10F 5A,10C 10I 5A,10A 12A 6B Is1,11D 12E 9B 9I,11H 12D 9A 9G,11A 11F 11G 12G,12B 12F 9D 9E,11I 9C 9H 9F Is3,11B 11C 8B,8A 8B,12C 12H,,7A 8A Ge1,10B 12A 12B 12G 12H,10F 11F 12D 6A 8A,11A 12E 6B 8A 9F,10A 10E 11D 11H 8A,10D 10G 12F 5A 7A Ge2,10H 11B 9C 9G,10C 10I 11G 9A,11C 12I 8B 9D,11E 11I 8B 9H,12C 9B 9E 9I Re1,11E 12E 5A 11G 7A,11A 12B 12C 12F 6B,11B 11H 11I 8B,11C 11D 12H 8A 11F,12A 12D 12G 12I 6A Re2,10I 9A 9H,9C 9E 9I 10F,10A 10B 9B,10D 10E 9G 9D,10C 10H 9F 10G Ti1,,9C 10I 9D,10D 9C 9D,, Lg3Lg1,10A,10A,10A,10A,10A Lg2Lg1,11A 9A,11A 9A,11A 9A,11A 9A,11A 9A ex4Lg1,12A,12A,12A,12A,12A Lg1,12A,11A,8A,,8A Ec1,10A 10D 11C 10B,10I 11F 11G,11A 11D 11E,10C 10G 10H 11B,10E 10F 11I 11H Fs1,9E 9H 9I,12I 9B 9C,12A 12B 12C 12D,12F 12G 9A 9G,12H 9D 9F 12E Ps1,,10H 11D,10E 10I 10B,10A 10D,11I 10C Es1,5A 6B,10G 10F,,6A, Em1,8B 9A 9F,5A 6B 9B 9G,9C 9H 7A,6A 8A 9D 9I,7A 8A 8B 9E Et1,8A 6B,7A 8B,,5A 6A, Ev1,10A 10F 6A,8A 10B 10G,10C 10H 7A,6B 10D 10I,5A 8B 10E Lg3,,,,,10A Lg2,,,,9A, N02,11F 11H,11F 11H 5A 7A,11F 11H 7A 9D,11F 7A 8B,11H 5A 8A N02N12,11C 12D 9D,12D,11C,12D 9D,11C 9D N03ex1,11I 9H,9E 9H,11I,11I 9E,9E 9H N03,11I 9E 9H,10H 11I,10H 9E 9H,10B 11I 9H,10B 11I 9E N10N06,10F 9F,,9F,10F 9F,10F N10,12B,12B 9F,10F,12B,12B N05,9A,12G 9G,12G 9A 9G,12G 9G,12G 9A N05ex2,9G,,9G,,9G N09N14,12F,12F 9I,12F 9I,9I, N14,9I,,,9I,9I N04,10A 11B 9B 9C,11B 12A,10A 11B 12A,12A,11B 12A N09,10C 12F,10D,12F,12F,10C 12F N09N01,10D,,,10D,10D N13,6A,,6A 6B,,6B N07,11A,9B,10E 11A,11A,10E 11A 9B N07N13,10E,10E,,10E, N11ex3,10G,10G,,,10G N06,12H 9F,10F 12H,10G 12H,12H,10G 9F N03N12,,10H,10H,10H, ex3N01,,10I,10I,,10I N01,11D 12D 12I,11D 12C 12I,12C 12D 12I,10I 11D 12C 12D 12I,11D 12C 12D N13N04,,11B 9B,,11B 9B,11B 9B N12,,11C,11C,11C,11C N07N01,11D,11D,11D,, N11,11E,,11E,11E,11E N11ex2,,,11E,11E,11E ex2ex3,,11F,11F,11F, N08,12E,11G 12E,11G 12E,11G,11G 12E N07N08,11G,,,11G,11G N10N03,,11H,11H,,11H ex2N01,12C,12C,,,12C N06ex2,12H,12E 12H,12H,12E,12E N11N05,12G,12G,,12G, N11N01,,12I,12I,12I, N07N04,,9C,9C,9C,
Nu salvăm ca atare, distribuţia finală DS – dar nu fiindcă o putem reconstitui oricând (prin fromRecast()) din "re_distr.csv", ci pentru motivul că mai departe avem de vizat pe rând, lecţiile fiecărei zile în parte. Să constituim un „dicţionar” care să asocieze fiecărei zile, lecţiile corespunzătoare acesteia:
lDS <- vector("list") for(zi in Zile) lDS[[zi]] <- DS %>% filter(zl == zi) %>% select(prof, cls) saveRDS(lDS, file = "dict_days.RDS") # zi ==> tabelul prof|cls al zilei
Desigur, era „mai simplu” lDS <- DS %>% split(.$zl) – dar aşa s-ar fi păstrat şi câmpul $zl, ori acesta este inutil pentru lecţiile unei aceleiaşi zile.
Acum în dict_days.RDS avem o listă cu 5 obiecte de tip data.frame, reprezentând fiecare cele 252 de lecţii prof | cls ale câte unei zile; urmează să montăm pe fiecare câte o coloană $ora, în care să alocăm fiecărei lecţii din ziua respectivă, câte o oră 1..7 (evitând desigur, anumite conflicte de alocare).
vezi Cărţile mele (de programare)