Ce relație avem între aria pătratului $ABCD$ și aria triunghiului $CLM$?

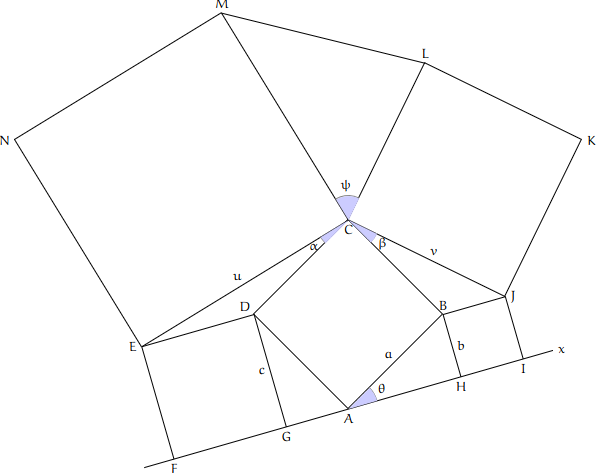
Este dat un pătrat $ABCD$ (vom nota mai mereu în sens antiorar) de latură $a$ și o dreaptă $Ax$ care trece prin vârful $A$ și este înclinată cu unghiul $\theta$ ($<\pi/2$) față de latura $AB$ (pentru $\theta=0$ avem cazul tratat separat în [1]). Fie $H$ și $G$ proiecțiile pe $Ax$ ale vârfurilor $B$ și $D$; se consideră pătratele $BHIJ$ (cu latura $b=BH$) și $DEFG$ (cu latura $c=DG$); pe segmentele $CJ=v$ și $CE=u$ se ridică pătratele $CJKL$ și $CMNE$.

Fie $\alpha$, $\beta$ și $\psi$ unghiurile din vârful comun $C$, ale triunghiurilor $DCE$, $JCB$ și $MCL$; avem imediat $\psi=2\pi-3\pi/2-(\alpha+\beta)=\pi/2-(\alpha+\beta)$ — astfel că vom putea obține aria triunghiului $MCL$ (în care $CM=u$ și $CL=v$) prin: $$\sigma(MCL)=\dfrac{uv}{2}\cos(\alpha+\beta) \tag{1}$$

Să observăm că nu va fi necesar să calculăm unghiurile $\alpha$ și $\beta$ (dificil de exprimat direct, cum am văzut în [1]), ci doar valorile de $\sin()$ și $\cos()$ ale acestora; iar dacă am calcula aria pentru triunghiurile $DCE$ și $JCB$ — atunci vor rezulta imediat și valorile $\sin(\alpha)$, $\sin(\beta)$.

Să observăm că în triunghiurile $DCE$ și $DAG$, unghiurile din vârful comun $D$ sunt suplementare și laturile din $D$ sunt respectiv egale; dar două triunghiuri cu câte două laturi respectiv egale și cu unghiurile formate de acestea, suplementare… au aceeași arie!
($0.5\times x y \sin(\phi)$, respectiv $0.5\times x y \sin(\pi-\phi)$; dar $\sin(\phi)=\sin(\pi-\phi)$).

Deci $\sigma(DCE)=\sigma(DAG)$ și $\sigma(BJC)=\sigma(BAH)$.
Dar $\triangle DGA \cong \triangle AHB$ (unde "$\cong$" desemnează congruența, sau „egalitatea”) fiindcă sunt dreptunghice, au ipotenuzele egale cu $a$ și unghiurile din $D$ și $A$ sunt congruente (având laturile respectiv perpendiculare); catetele lor au lungimile $b$ și $c$.

Deci $\sigma(DCE)=\sigma(BJC)=\dfrac{bc}{2}$; pe de altă parte, $\sigma(DCE)=\frac{1}{2}au\sin\alpha$ și $\sigma(BJC)=\frac{1}{2}av\sin\beta$. Rezultă:

Prin teorema cosinusului, din $\triangle{DCE}$ avem $u^2=a^2+c^2-2ac\cos(\pi-\theta)$, iar din $\triangle{BJC}$ avem $v^2=a^2+b^2-2ab\cos(\pi/2+\theta)$; ținând seama că $b=a\sin\theta$ și $c=a\cos\theta$, obținem:

(și fiindcă $b^2+c^2=a^2$, avem interpretarea (mai mult sau mai puțin interesantă): pătratele construite pe $u$ și $v$ acoperă împreună de 5 ori aria pătratului $ABCD$)

Ținând seama de (2), avem: $\cos^2\alpha=1-\sin^2\alpha=\dfrac{a^2u^2-b^2c^2}{a^2u^2}$ și $\cos^2\beta=\dfrac{a^2v^2-b^2c^2}{a^2v^2}$.
Dar ținând seama de (3) și de exprimările în funcție de $a$ și $\theta$ pentru $b$ și $c$, avem
$a^2u^2-b^2c^2=a^4(1 + 3\cos^2\theta-\cos^2\theta\sin^2\theta)=a^4(1+2\cos^2\theta+\cos^4\theta)=a^4(1+\cos^2\theta)^2$; analog, găsim $a^2v^2-b^2c^2=a^4(1+\sin^2\theta)^2$. Rezultă:

Prin urmare, $\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta=\dfrac{a^2}{uv}(2+\cos^2\theta\sin^2\theta)-\dfrac{b^2c^2}{a^2uv}$,
dar $bc=a^2\sin\theta\cos\theta$ și rezultă:

Din (1) și (4) obținem că

adică, pătratul $ABCD$ și triunghiul $MCL$ au aceeași arie.

Cum construiești… un pătrat?!

MetaPost este un limbaj de programare prin care putem genera (mai ales, vectorial) obiecte grafice, pe baza unor descrieri matematice simbolice; am avut anterior, mai multe prilejuri de a formula programe MetaPost și acum doar punctăm câteva aspecte, legate de modul în care am produs figura de mai sus.

De data aceasta n-am apelat (clasic) la compilatorul mpost – ci am folosit (sub o documentare expeditivă) lualatex cu pachetul luamplib, pe un fișier "figsql.tex" structurat cam așa:

\documentclass{standalone}
\usepackage{luamplib}
\begin{document}
    \begin{mplibcode}
        % ...
        defaultfont := "eurm10";
        defaultscale := 8/fontsize(defaultfont);
        % ...
        % def marking ...  (macrou de etichetare a punctelor unui contur)
        % ...
        beginfig(1);
            % ... (descrierea figurii)
        endfig;
    \end{mplibcode}
\end{document}

După încorporarea sub beginfig(1) a descrierii MetaPost a figurii respective, rezultatul se obține ca fișier PDF, invocând lualatex figsql.tex. Avantajul de care m-am bucurat față de maniera clasică (dar repet: m-am documentat foarte sumar) constă în ușurința specificării de etichete; pentru figura de aici am folosit fontul matematic eurm10 (a compara cu fontul „standard” al etichetelor din figurile redate în [1]).

Prin standalone, pagina PDF este trunchiată la boxa care conține figura respectivă, încât figura va putea fi încorporată imediat în locul dorit dintr-un fișier LaTeX în care ea este necesară; desigur, dacă e să redăm figura pe un site HTML (ca aici), atunci ar cam trebui să transformăm din PDF în PNG — dar putem obține figura și direct în format PNG, prin:

\documentclass[convert = {ghostscript}]{standalone}

Ca să poată invoca Ghostscript (care să convertească PDF-ul în PNG), lualatex (sau un alt compilator de LaTeX) trebuie apelat cu opțiunea shell-escape (altfel, din rațiuni de securitate, invocarea de programe externe este inhibată).

Figura noastră este destul de simplă (nu conține curbe, tangente, sau intersecții de căi complicate), așa că (având nevoie de figură, nu de program) am descris-o cât se poate de banal: am declarat toate punctele (prin pair A,B,C,...,M,N,X;), am definit pătratul ABCD și dreapta Ax, apoi am definit celelalte puncte (folosind repetat macro-urile uzuale dotprod(), whatever() și rotatedaround()) și am trasat pătratele asociate, iar în final am etichetat diverse elemente folosind label() pentru fiecare în parte (mai nebanală poate, a fost marcarea unghiurilor – pentru care am refolosit macro-ul markang, constituit deja în Construcţii prin asemănare (în MetaPost)).

Acum măcar, să ne gândim cât de cât și la maniera de programare (încât altădată, poate să ne mai scutim de chinul descrierii mecanice, „punct cu punct” și etichetă cu etichetă).
Dar… ne putem aștepta și la această concluzie: calea „banală” este cea mai bună!

Avem multe puncte de etichetat, dar nu este necesar să le declarăm ca atare: putem folosi definiția globală existentă "pair z[]" și doar la etichetare, să indicăm literele respective; de exemplu, label("A", z0) va eticheta punctul z0 cu litera A din fontul specificat în variabila defaultfont (și nu este necesar label(btex $A$ etex, z0), ca sub clasicul mpost).

Primind un contur (variabilă de tip path) P și indexul unui caracter din fontul curent, următorul macrou etichetează punctele caracteristice ale lui P, folosind caracterele consecutive începând cu cel dat; fiecare etichetă este plasată pe direcția perpendiculară pe conturul respectiv, la o aceeași mică distanță față de punct:

def cling(expr P, icod, sgn) =
    n := length(P) - 1;
    pair Z;
    for t=0 upto n :
        Z := point t of P;
        label(char(t+icod), 
              7 unitvector(direction t of P) rotated(sgn*90) shifted Z
        ) withcolor .1black;
    endfor;
enddef;

Am introdus ulterior și parametrul sgn $=\pm 1$, drept remediu ad-hoc pentru cazul când literele ar apărea în interiorul conturului și nu cum vrem, spre exteriorul acestuia… („remediul” bun ar folosi turningnumber, în loc de un parametru "sgn" – dar nu mai disecăm aici lucrurile).
De exemplu, următoarea „figură” descrie și trasează un pătrat cu diagonala pe axa orizontală, etichetând apoi vârfurile prin cling():

beginfig(1);
    z0 = (0cm, -2cm); z1 = (2cm, 0cm); 
    z2 = -z0; z3 = -z1;
    path P; P = z0 -- z1 -- z2 -- z3 -- cycle;
    draw P withpen pencircle scaled 0.5;
    cling(P, 75, -1);  % 75 este indexul literei "K"
    %%% continuarea figurii...
endfig;

Dar avem două categorii de pătrate: cu o latură perpendiculară dintr-un punct dat pe o dreaptă dată (cum sunt pe figura noastră, $BHIJ$ și $DEFG$) și respectiv, ridicate pe un segment dat (cum sunt $CJKL$ și $CMNE$); le putem genera prin următoarele două macro-uri:

vardef sq_point_line(expr A, U, V, sgn) =
    pair Z[];
    (A - Z0) dotprod (V - U) = 0;  % vectorii AZ0 și UV sunt perpendiculari
    Z0 = whatever[V, U];  % Z0 este pe dreapta UV
    Z1 = A rotatedaround(Z0, sgn*90);  % vârful opus lui A
    Z2 + Z0 = A + Z1;  % Z2 este simetric cu Z0 față de diagonală
    A--Z0--Z1--Z2--cycle
enddef;
vardef sq_on_line(expr U, V, sgn) =
    pair Z[];
    Z0 = U rotatedaround(V, sgn*90);
    Z1 + V = U + Z0;
    U--V--Z0--Z1--cycle
enddef;

Cu cele trei macro-uri schițate mai sus, figura poate fi generată astfel:

beginfig(2);
    pickup pencircle scaled 0.4;  % grosimea implicită a peniței
    path P[];  % contururile pătratelor

    z0 = (0cm, -2cm); z1 = (2cm, 0cm);  % vârfurile A și B
    z2 = -z0; z3 = -z1;  % rezultă vârfurile C și D
    P0 = z0--z1--z2--z3--cycle;  draw P0;
    cling(P0, 65, -1);  % pătratul ABCD

    pair X[]; X1 = (5cm, 0);  X2 + X1 = 2*z0;
    draw (X2 -- X1) withpen pencircle scaled 0.2;  % dreapta Ax

    P1 = sq_point_line(z1, z0, X1, -1);  draw P1;
    cling(subpath(1,4) of P1, 72, -1);  % pătratul BHIJ

    P2 = sq_point_line(z3, z0, X1, 1);  draw P2;
    cling(subpath(3,0) of P2, 69, -1);  % pătratul DEFG

    P3 = sq_on_line(point 2 of P0, point 3 of P1, -1);  draw P3;
    cling(subpath(2,4) of P3, 75, -1);  % pătratul CJKL
    
    P4 = sq_on_line(z2, point 3 of P2, 1);  draw P4;
    cling(subpath(3,1) of P4, 77, -1);  % pătratul CMNE
endfig;

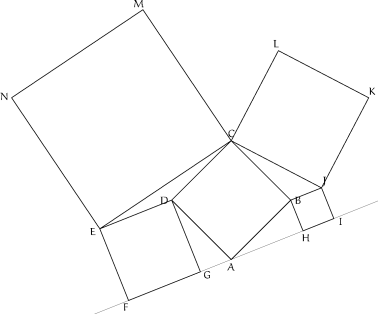
Desigur, văzând cum au fost poziționate etichetele "J", "B", "D" și constatând că a trebuit să restrângem unele căi, prin subpath() (când pe două vârfuri avem deja, etichete)… rămâne de „îmbunătățit” sau de completat definiția macrou-lui cling() (sau… de abandonat, în favoarea programului „banal”; sau… de făcut figura respectivă printr-un program PostScript (v. [2]), sau mai simplu, printr-un program R).

Dar precizăm că până să constituim programul redat mai sus, am încercat varianta (și ea, nebanală) care pleacă de la conturul predefinit unitsquare și îi aplică transformări – rotații cu anumite unghiuri $\theta$, scalări și translații; numai că, implicarea repetată în calculele necesare a unor funcții precum cosd($\theta$) a condus prin acumularea erorilor de aproximare, la faptul că pe figura produsă dreptele $HI$ și $FG$ deviază vizibil față de punctul $A$!
Am abandonat atunci ideea și… am ajuns la programul redat mai sus.

Însă ideea de a pleca de la un contur predefinit și a-i aplica transformări afine pentru a ajunge la figura de mai sus, este în sine foarte bună și conduce firesc la o generalizare a problemei: dacă în loc să plecăm de la un pătrat, am pleca de la un patrulater convex oarecare $ABCD$ și am construi patrulatere asemenea cu $ABCD$, poziționate ca în problema cu pătrate – ce relație ar rezulta între aria triunghiului $CLM$ și aria patrulaterului $ABCD$?