În [1] ordonasem profesorii („cel mai bine”, aşa) după "betweenness" – în fond, după numărul de geodezice (drum de lungime minimă între două noduri) pe care se află profesorul, într-un graf în care profesorii sunt adiacenţi dacă au măcar o clasă comună; însă ordinea claselor a fost lăsată chiar la voia întâmplării…
Este adevărat că în programul nostru, parcurgerea în ordine aleatorie a listei claselor este esenţială pentru obţinerea unui orar; totuşi, unele clase ar trebui să fie cumva favorizate – de exemplu, o clasă care are 4 ore ar fi de abordat înaintea celor cu 6 ore, fiindcă altfel, întâlnind-o mai spre sfârşit, cel mai adesea profesorii acelei clase ar avea deja ocupate primele 4 ore.

Sensul permutării aleatoare

Următorul mic experiment arată că are sens să vizăm nu chiar la întâmplare, elementele unui set de date – „favorizând” pe cât se poate (totuşi, aleatoriu) poziţionarea unora faţă de celelalte.

Să producem nişte permutări oarecare pentru literele 'A'..'J' – dar astfel încât literele să apară, cu unele excepţii întâmplătoare, în ordine inversă celei obişnuite.
Pentru aceasta, „ponderăm” crescător literele şi folosim – de vreo sută de ori – sample(), cu parametrul 'prob' indicând ponderile respective; apoi transformăm lista celor 100 de permutări obţinute, într-o matrice de tip 100×10 şi contorizăm (într-o matrice 10×10) fiecare literă (în cele 100 de linii), pe fiecare poziţie 1..10:

AJ <- LETTERS[1:10]
wgt <- seq(10, 1000, by=100)
names(wgt) <- AJ
    # > wgt
    #   A   B   C   D   E   F   G   H   I   J 
    #  10 110 210 310 410 510 610 710 810 910 
lst <- lapply(1:100, function(i) sample(AJ, prob = wgt))
mx <- t(do.call(cbind, lst))
#    > mx
#           [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
#      [1,] "I"  "J"  "E"  "F"  "C"  "G"  "H"  "D"  "B"  "A"  
#      [2,] "C"  "H"  "J"  "I"  "G"  "B"  "D"  "F"  "E"  "A"  
#      [3,] "H"  "I"  "B"  "G"  "E"  "F"  "D"  "J"  "C"  "A"  
## ...
#     [99,] "J"  "I"  "G"  "H"  "B"  "D"  "F"  "E"  "C"  "A"  
#    [100,] "J"  "H"  "I"  "G"  "F"  "D"  "C"  "E"  "B"  "A" 
cnt_lett_pos <- function(ltt, col) {
    sum(mx[, col] == ltt)
}  # frecvenţa unei litere pe o coloană a matricei de permutări
cnt <- matrix(0, nrow=10, ncol=10, byrow=TRUE)
row.names(cnt) <- AJ
for(i in 1:10)
    for(j in 1:10)
        cnt[i, j] <- cnt_lett_pos(AJ[i], j)
print(cnt)
    # > cnt
    #   [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
   # A    0    0    0    0    0    1    1    2    3    93
   # B    4    4    3    6    5    9    7   14   44     4
   # C    6    2    8    6    7    8   16   10   35     2
   # D   10    6    8    9    9   14   15   24    5     0
   # E   13    7   16    7   14   10    8   16    8     1
   # F    6   11    9   18   12   11   19   12    2     0
   # G   10   13   17    9   15   19   10    6    1     0
   # H   18   18   11    9   16   10   10    7    1     0
   # I   16   18   14   18   11    9    8    6    0     0
   # J   17   21   14   18   11    9    6    3    1     0

La fiecare execuţie obţinem alte rezultate (fiindcă nu am utilizat set.seed()); dar în general (cum se vede mai sus), literele 'A'..'D' apar foarte rar pe primele poziţii (şi apar cel mai adesea, pe ultimele poziţii ale permutărilor) şi cel mai adesea, pe primele poziţii apar ultimele litere – deci putem zice că, exceptând unele cazuri, în permutările obţinute literele sunt poziţionate „descrescător”.

Ponderarea claselor

Într-un graf al claselor – adiacente în măsura în care au vreun profesor comun – acele clase care au puţine ore (4 ore) vor fi situate pe un număr mai mic de drumuri, faţă de cele care au multe ore; deci am putea considera iarăşi ordonarea după "betweenness". Pentru cazul considerat anterior (241 de lecţii, cu 68 de profesori, pe 40 de clase), folosind pachetul igraph la fel ca în programul redat în [2] – obţinem această imagine a claselor:

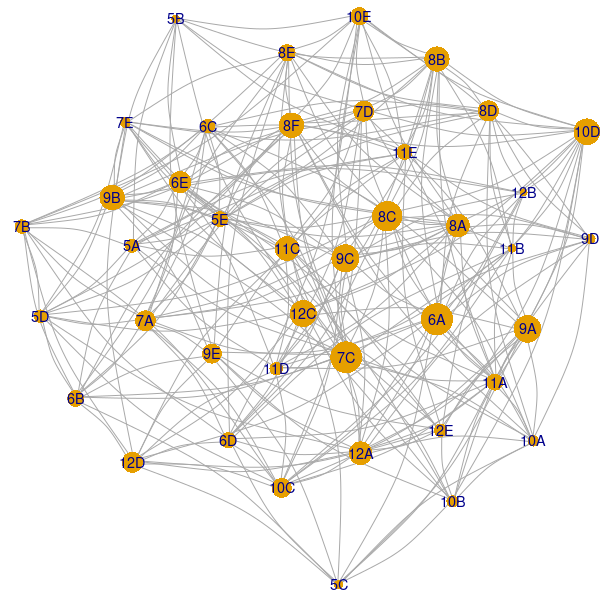
Mărimea de reprezentare a vârfurilor corespunde coeficienţilor "betweenness"; clasele '12B' şi '5B' au în ziua respectivă câte doar 4 ore şi au într-adevăr, cei mai mici coeficienţi. De pe imagine, ordinea în care ar trebui abordate clasele ar fi, aproximativ: 12B, 5B, 11B, ..., 9C, 8C, 7C, 6A; cu o asemenea ordine a claselor, avem şansa ca durata în care va rezulta un orar să fie mai scurtă, decât în cazul anterior (când tratam clasele în mod uniform).

Probabil că şi mai bine ar fi să luăm în calcul nu numai coeficienţii "betweenness" din graful de mai sus, dar şi numărul de profesori comuni, la fiecare două clase…

Modificarea programului

Faţă de programul din [1], modificarea importantă constă în înlocuirea secvenţei care producea coeficienţii "betweenness" pentru graful profesorilor, cu următoarea funcţie – care furnizează coeficienţii respectivi pentru profesori sau pentru clase, după cum este apelată cu indexul coloanei $prof, sau cu cel al coloanei $cls:

get_betweenness <- function(col) {  # 1: 'prof'; 2: 'cls'
    V <- lessons %>% distinct(.[[col]]) %>% pull()  # şirul numelor din coloană
    len <- length(V)
    adjm <- matrix(rep(0, len), nrow=len, ncol=len, byrow=TRUE, 
                   dimnames=list(V, V))  # matricea de adiacenţă

    col1 <- ifelse(col == 1, "prof", "cls")
    col2 <- ifelse(col == 1, "cls", "prof")
    neigh_of <- function(X) {
        lessons %>% filter(.[[col1]] == X) %>% 
        distinct(.[[col2]]) %>% pull()
    }
    adj_of <- function(X) {
        lessons %>% 
        filter(.[[col1]] != X & .[[col2]] %in% neigh_of(X)) %>% 
        distinct(.[[col1]]) %>% pull()
    }
    for(X1 in V)
        for(X2 in adj_of(X1))
            adjm[X1, X2] <- 1

    G <- igraph::graph_from_adjacency_matrix(adjm, mode="undirected")
    igraph::betweenness(G, directed=FALSE)  # returnează coeficienţii
}

Mai departe, ordonăm profesorii (mai încolo şi clasele) după coeficienţii returnaţi de funcţia introdusă mai sus:

btw_prof <- get_betweenness(1) %>% sort()
btw_cls <- get_betweenness(2) %>% sort()  # 100*get_betweenness(2) %>% sort(.)
task <- lessons %>%
        mutate(prof = factor(prof, 
                      levels = names(btw_prof), ordered=TRUE)) %>%
        arrange(prof, cls)
hBits <- rep(0L, nlevels(task$prof))  # alocările de ore (biţi) la profesori
names(hBits) <- levels(task$prof)

Apoi, despărţim lecţiile după clase, instituim un „vector cu nume” pentru clase şi ponderile „betweenness” asociate şi – în vederea testării – ciclăm de vreo 10 ori secvenţa de producere a unui orar (afişând timpii şi numărul de ferestre şi salvând desigur, orarele respective):

prnTime()  # print(strftime(Sys.time(), format="%H:%M:%S"), quote=FALSE)
Z <- task %>% split(.$cls)
lstCls <- names(Z)
btw_cls <- btw_cls[lstCls]  # numele claselor şi ponderile asociate
for(s in 1:10) {
    odf <- vector("list", length(lstCls))  # înregistrează orarele claselor
    while(TRUE) {
        succ <- TRUE
        bith <- hBits  # reiniţializează octeţii de alocare pe orele zilei
        lstCls <- sample(lstCls, prob = btw_cls)  # ordine aleatorie ponderată
        for(K in lstCls) {
            W <- mountHtoCls(Z[[K]])  # încearcă un orar pentru clasa curentă
            if(is.null(W)) {
                succ <- FALSE 
                break  # abandonează în caz de insucces
            }
            odf[[K]] <- W  # salvează orarul constituit clasei curente
        }
        if(succ & sum(unlist(lapply(bith, holes))) <= nGaps) break
    }
    orar <- bind_rows(odf)  # reuneşte orarele claselor
    prnTime()  # afişează H:M:S
    print(sum(unlist(lapply(bith, holes))))  # numărul de ferestre
    saveRDS(orar, file=paste0("orar.", s, ".RDS"))  # prof|cls|ora 
    write_csv(orarByProf(orar), file="orars.csv",  
              na="-", col_names=TRUE, append=TRUE)
}

Am renunţat, faţă de [1], să mai salvăm şi vectorul octeţilor de alocare 'bith (fiind uşor de restabilit de pe orar, dacă va fi necesar).

Iată o mostră de execuţie a programului reconstituit mai sus:

> rm(list = ls())
> source("daySchoolSchedule.R")
[1] 08:11:22  # momentul lansării
[1] 08:14:54  # momentul obţinerii orarului
[1] 26  # numărul de ferestre din orar
[1] 08:17:44
[1] 30
[1] 08:18:06
[1] 30
[1] 08:34:12
[1] 29
[1] 08:35:38
[1] 30
etc.

În experimentele noastre (pe 241 de lecţii, cu 68 profesori şi 40 clase), durata medie a producerii unui orar (cu maximum 30 de ferestre) este cam de 3-4 minute – ceea ce înseamnă o îmbunătăţire cam de trei ori, faţă de versiunea din [1]. Această îmbunătăţire (chiar importantă) decurge din faptul că acum am ordonat clasele nu chiar la întâmplare (cum procedam în [1]), ci ţinând cont şi de coeficienţii "betweenness" ai acestora, din graful de clase introdus mai sus.