Care este (sau, cum determinăm) numărul minim de instrucţiuni curveto (cubice Bézier) pentru a reprezenta o curbă indicată (cu diferenţe imperceptibile la scară uzuală, faţă de graficul trasat - pe ecran sau pe hârtie - printr-un număr mare de puncte)?

Ecuaţiile parametrice şi derivatele acestora pentru semicardioida $\mathscr{K}$ sunt (v. [2]): $$x(t)=2t(2t-1),\;y(t)=4t\sqrt{t(1-t)},\;t\in[0,1]$$ $$x'(t)=2(4t-1),\;y'(t)=2(3-4t)\sqrt{\frac{t}{1-t}}$$ În [1] ajunsesem la o reprezentare cu 9 instrucţiuni curveto a lui $\mathscr{K}$, printr-un program PostScript generic (aplicabil mutatis mutandis şi altor curbe), care segmenta intervalul $[0,1]$ în părţi egale şi determina pentru fiecare parte punctele de control necesare aproximării prin curveto a porţiunii corespunzătoare a lui $\mathscr{K}$; calculam punctele de control folosind derivatele în capetele subintervalului, lovindu-ne astfel şi de situaţia dilematică $y'(1)=\infty$ (când a trebuit să experimentăm asupra valorii "teoretice").

A devenit clar că este mai bine dacă segmentăm curba nu prin puncte legate arbitrar la valorile $i/N,\,i=1..N$ ale parametrului $t$, ci prin unele puncte caracteristice ei (puncte de extrem, de inflexiune, etc.). Pe de altă parte, ne-a devenit clar că este mai avantajos să folosim MetaPost: operatorul desemnat prin ".." (denumit "path_join") creează o cubică Bézier care uneşte cele două puncte care îi sunt indicate (împreună eventual, cu direcţia tangentei), angajând intern anumiţi algoritmi (destul de complicaţi pentru a ne feri să-i explicăm noi) de determinare a punctelor de control (spre deosebire de PostScript, în care nu avem decât posibilitatea de a le specifica noi înşine).

Avem $x'(\frac{1}{4})=0$ (cu $y'(\frac{1}{4})\ne 0$), deci în punctul $(x(\frac{1}{4}), y(\frac{1}{4}))=(-\frac{1}{4}, \frac{\sqrt{3}}{4})$ tangenta la $\mathscr{K}$ este verticală.
$y'(1)/x'(1)=\infty$, deci în $(x(1),y(1))=(2,0)$ tangenta este verticală.
$y'(0)=y'(\frac{3}{4})=0$, deci tangentele în $(0,0)$ şi $(\frac{3}{4},\frac{3\sqrt{3}}{4})$ sunt direcţionate orizontal.

Un alt punct important este $(x(\frac{1}{2}),y(\frac{1}{2}))$, fiindcă punctele lui $\mathscr{K}$ provenite din valori ale parametrului $t$ simetrice faţă de mijlocul $\frac{1}{2}$ al intervalului $[0,1]$ sunt legate (două câte două) prin proprietăţi semnificative (suma distanţelor la origine este egală cu 2; $Oy$ bisectează unghiul razelor polare ale celor două puncte; etc. - v. [2]).
Avem $x'(\frac{1}{2})=y'(\frac{1}{2})=2$, deci tangenta în $(x(\frac{1}{2}),y(\frac{1}{2}))$ este paralelă cu prima bisectoare a sistemului de axe.

Cele cinci "puncte importante" evidenţiate mai sus corespund într-adevăr, împărţirii intervalului $[0,1]$ în patru subintervale egale; dar acum am ajuns la ele plecând de la proprietăţi ale funcţiei (legate de direcţia tangentelor), în loc de a asuma din start ca în [1], o partiţionare echidistantă pe $[0,1]$ (independentă de funcţie).
Notând cu z1, ..., z5 punctele lui $\mathscr{K}$ rezultate pentru $t=\frac{i}{4},\,i=0..4$, putem formula conturul z1{left}..z2{up}..z3{dir 45}..z4{right}..{down}z5, însemnând în MetaPost constituirea şi îmbinarea a patru cubice Bézier: prima pleacă orizontal spre stânga din z1, curbează după punctele sale de control şi ajunge vertical în z2; a doua continuă spre z3, ajungând aici la 45 de grade faţă de orizontală; ş.a.m.d.

Un program MetaPost prin care să evidenţiem acest contur şi deasemenea (pentru comparaţie) conturul obţinut prin marcarea unui număr suficient de mare de puncte ale lui $\mathscr{K}$, se poate formula într-un fişier "smcd.mp" ca definiţie de figură beginfig(1); ... endfig. Dar în principiu, în prealabil avem de setat anumite aspecte grafice (fontul de utilizat pentru etichetare, o scalare şi poziţionare în pagină convenabile, etc.) şi de formulat subrutine generice sau macro-uri de care vom avea nevoie în diverse definiţii de figură (astfel, smc_point(t) modelează ecuaţiile lui $\mathscr{K}$; scardioid foloseşte smc_point pentru a produce o variabilă de tip 'picture' care la instanţiere, va marca un anumit număr de puncte ale lui $\mathscr{K}$; path_nodes etichetează nodurile conturului primit ca argument, poziţionând eticheta pe direcţia normalei la contur în punctul respectiv):

outputtemplate := "%j-%c.eps";  % produce fişiere "smcd-1.eps", "smcd-2.eps", etc.
prologues := 3;  % asigură înglobarea fontului, în fişierul EPS produs
defaultfont := "phvr8r";  % fontul 'Helvetica' (vom eticheta nodurile conturului)
defaultscale := 1.2;  % măreşte caracterele de la 8 la 8*1.2 puncte tipografice
% măreşte de 200 de ori; mută originea spre dreapta cu 10bp şi în sus cu 100bp:  
def scale_shift = scaled 200 shifted (10, 100) enddef;

vardef smc_point(expr t) =  % punctul semicardioidei asociat lui t∈[0,1]
    (2*t*(2*t-1), 4*t*sqrt(t*(1-t)))
enddef;
def scardioid =  % trasează semicardioida prin 100 de puncte (instrucţiuni 'lineto')
    image(
        pickup pencircle scaled 2.3;
        for t = 0 step .01 until 1:
            draw smc_point(t) scale_shift withcolor (1, 0.3, 0);
        endfor
    )  % variabilă de tip 'picture' (o vom putea instanţia în oricare figură)
enddef;

def path_nodes(expr q) =  % marchează nodurile conturului
    pickup pencircle scaled 3; pair Z;
    for t=0 upto length(q):
        Z := point t of q;
        draw Z;  % marchează nodul şi îl etichetează pe direcţia normalei la curbă
        label(decimal(t+1), 7 unitvector(direction t of q) 
                            rotated(-90) shifted Z) withcolor .1black;
    endfor
enddef;

beginfig(1);  path p;  % "conturul" este o variabilă de tip 'path'
    z1 = (0, 0);  % nodul cardioidei  (tangentă orizontală)
    z2 = (-1/4, sqrt(3)/4);  % cel mai din stânga punct (cu tangentă verticală)
    z3 = (0, 1);  % pentru t=0.5; tangenta este paralelă cu prima bisectoare
    z4 = (3/4, (3*sqrt(3))/4);  % cel mai de sus punct (cu tangentă orizontală)
    z5 = (2, 0);  % vârful cardioidei (tangentă verticală)
    p = ( z1{left}..z2{up}..z3{dir 45}..z4{right}..{down}z5 )  scale_shift;
    pickup pencircle scaled 0.8;  % grosimea peniţei 
    draw p withcolor .78blue;  % cele 4 cubice Bézier (cu nuanţă de albastru)
    path_nodes(p);  % marchează şi etichetează capetele arcelor Bézier
    draw scardioid;  % instanţiază semicardioida conturată prin 'lineto'
endfig;

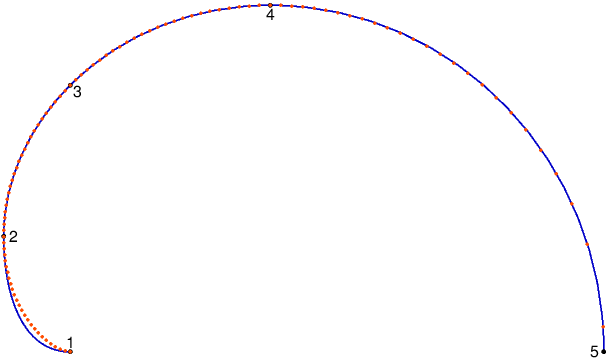
Invocând compilatorul de MetaPost, prin mpost smcd.mp, obţinem fişierul "smcd-1.eps" reflectat (printr-un "Document Viewer", ca evince) în imaginea de mai sus; deschizând într-un editor de cod-sursă (ca gedit), putem identifica uşor liniile asociate în PostScript (prin compilarea programului de mai sus cu mpost) celor patru operatori '..':

newpath 10 100 moveto
-26.74011 100  -40 144.2627  -40 186.60278 curveto
-40 229.53186  -20.38635 269.61365  10 300 curveto
49.55688 339.55688  104.02466 359.80835  160 359.80835 curveto
299.88953 359.80835  410 241.73889  410 100 curveto stroke

Dacă am înscrie deasupra acestor 5 linii %!PS (şi apoi linia 50 100 translate, având în vedere că prima instrucţiune curveto are punctul final la abscisa -40) şi am salva fişierul ca "fig-1.ps", atunci deschizându-l în evince vom regăsi graficul celor 4 arce 1-2-3-4-5 din imaginea de mai sus.

Acuma, să observăm că arcul albastru care uneşte punctele 1 şi 2 (reprezentând prima instrucţiune curveto) diferă sensibil faţă de porţiunea (marcată prin puncte colorate "orange") din $\mathscr{K}$ pe care voia să o aproximeze; deasemenea, mărind figura (spre 200%, prin operaţiile obişnuite într-un "Document Viewer") putem sesiza că arcul albastru final 4--5 este puţin-puţin "deasupra" punctelor orange ale lui $\mathscr{K}$.

Este clar că pe $\mathscr{K}$ există un punct pe arcul 1--2 şi unul pe arcul 4--5 în care tangenta ajunge paralelă cu a doua bisectoare a sistemului de axe; pentru aceste puncte trebuie să avem $y'(t)=-x'(t)$, adică $(3-4t)\sqrt{t}=(1-4t)\sqrt{1-t}$.
Să observăm că această ecuaţie are "rădăcina străină" $\frac{1}{2}$ ("străină" fiindcă duce la "1=-1"); ridicând la pătrat şi ţinând seama că astfel se introduce ca rădăcină şi cea "străină", obţinem $32t^3-48t^2+18t-1=0\iff(2t-1)(16t^2-16t+1)=0$. Prin urmare, valorile $t$ care ne dau punctele lui $\mathcal{K}$ în care tangenta are panta egală cu $-1$ sunt $t_{1,2}=\frac{1}{2}\pm\frac{\sqrt{3}}{4}$.

Adăugăm programului MetaPost de mai sus o a doua figură, considerând acum - prin smc_point ($t_{1,2}$) - şi cele două puncte ale lui $\mathscr{K}$ determinate mai sus:

beginfig(2);
    numeric sq; sq = sqrt(3)/4;  % pentru a evita repetarea calculului
    z1 = (0, 0);  
    z2 = smc_point(0.5 - sq);  % tangenta face 135 grade cu Ox
    z3 = (-0.25, sq);  % tangenta ajunge în poziţie verticală
    z4 = (0, 1);  % tangenta este înclinată cu 45 grade
    z5 = (0.75, 3*sq);  % tangentă orizontală  
    z6 = smc_point(0.5 + sq);  % tangenta are direcţia egală cu (-45) grade
    z7 = (2, 0);  
    path p, q;
    p := z1{left}..z2{dir 135}..z3{up}..z4{dir 45}..z5{right}..z6{dir -45}..{down}z7;
    show p;  % afişează conturul constituit (variabila 'p') 
    q := p scale_shift;  % scalează 'p', în vederea trasării efective
    pickup pencircle scaled 0.8; draw q withcolor .78blue;
    path_nodes(q);  % marchează şi etichetează capetele arcelor Bézier
    draw scardioid;  % instanţiază semicardioida conturată prin 'lineto'
endfig;

end  % pentru a evita modul de lucru interactiv ("stop! NU mai am figuri/întrebări")

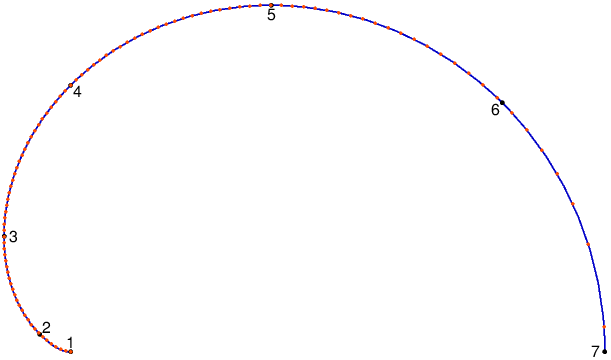
De data aceasta, reprezentarea lui $\mathscr{K}$ (schiţat cu 100 de puncte orange) prin cele 6 cubice Bézier (colorate albastru) este destul de "fidelă".

Fiindcă am folosit show p, compilatorul ne-a dezvăluit în fişierul "smcd.log" constituţia conturului (şi am optat pentru valorile dinaintea scalării acestuia); să preluăm din acest fişier conturul p indicat şi să adăugăm (înaintea declaraţiei "end") o nouă figură, în care să întruchipăm întreaga cardioidă (simetrizând p faţă de $Ox$ cu reflectedabout şi folosind apoi buildcycle) şi să trasăm conturul poligonal al punctelor de control pentru cele 6 cubice Bézier care formează semicardioida superioară:

beginfig(3);  % cardioida; poligonul punctelor de control
    path p, q, h, g, K;
    p = (0,0)..controls (-0.04654,0) and (-0.08301,0.03397)
 ..(-0.11603,0.06699)..controls (-0.21149,0.16245) and (-0.25,0.29778)
 ..(-0.25,0.43301)..controls (-0.25,0.64766) and (-0.15193,0.84807)
 ..(0,1)..controls (0.19778,1.19778) and (0.47012,1.29904)
 ..(0.75,1.29904)..controls (1.07574,1.29904) and (1.3856,1.16344)
 ..(1.61603,0.93301)..controls (1.86324,0.6858) and (2,0.34964)
 ..(2,0);  % semicardioida superioară (6 cubice Bézier)
    g = p reflectedabout((0,0), (2,0));  % semicardioida inferioară
    K = buildcycle(p, reverse g);  % "reuneşte", întruchipând cardioida
    fill (K scale_shift) withcolor .8white;
    q = p scale_shift;  % scaled 100 shifted (50, 300)
    path_nodes(q);
    h = point 0 of q for t=1 upto length(q): 
        --postcontrol t-1 of q -- precontrol t of q endfor 
        --point(length(q)) of q;  % conturul poligonal al punctelor de control
    draw h withpen pencircle scaled 0.75 withcolor (1, 0.3, 0); 
endfig;

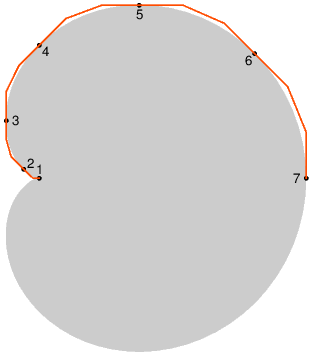
Arcul 1--2 având lungimea foarte mică, punctele de control ale sale n-au putut fi redate distinct (la scara folosită în program).

Punctele de control ale unei cubice Bézier sunt accesate prin postcontrol şi respectiv precontrol ("post" vizează pe cel care urmează nodului iniţial al arcului, iar "pre" pe cel dinaintea nodului final). Punctele de control au fost astfel alese, încât segmentul care ar uni "precontrolul" unui arc cu "postcontrolul" arcului Bézier următor să fie tangent curbei pe care arcele respective o aproximează (cum se şi vede pe figură); de aici şi ideea aplicată mai sus: pentru a reprezenta o curbă cu un număr cât mai mic de cubice Bézier alegem cumva câteva puncte ale curbei în care cunoaştem direcţiile tangentelor (şi montăm câte o instrucţiune curveto pentru fiecare două astfel de puncte, vecine la parcurgerea într-un acelaşi sens a curbei).
În MetaPost acest mecanism de calcul este implicit, cerându-se doar capetele arcului şi eventual, direcţia tangentei (la intrare sau/şi la ieşire) într-un capăt sau altul; el este implicit fiindcă nu se vizează o cubică Bézier ca atare (cum face curveto din PostScript), ci totdeauna, un contur format eventual (prin "path_join") din mai multe cubice Bézier înlănţuite ("înlănţuirea" acestora necesită corelarea tangentelor, evidenţiată mai sus).