Șabloanele binare ale multiplilor (I)
Graful următor prezintă un automat (finit determinist), descriind formarea unui cuvânt binar oarecare prin preluarea câte unui bit, începând cu cel mai semnificativ (dacă nu luăm în seamă posibilitatea de a prefixa cu biți 0 nesemnificativi), clasificându-l totodată ca număr modulo 3 (în funcție de nodul $\large\textrm{0}$, $\large\textrm{1}$ sau $\large\textrm{2}$ în care încheiem cuvântul):
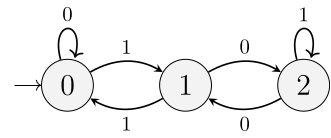
Cele 6 arce ale grafului, etichetate cu 0 sau cu 1, asigură funcționarea automatului, trecându-l din starea curentă în câte o nouă stare (sau chiar aceeași, în două cazuri). Starea inițială (marcată cu o săgeată externă grafului) este $\large\textrm{0}$; starea finală nu este indicată, permițând o anumită alegere: cuvântul binar generat reprezintă un multiplu de 3 dacă îl încheiem în starea $\large\textrm{0}$ sau reprezintă cu 1 sau cu 2 mai mult ca un multiplu de 3 dacă în final ajungem în starea $\large\textrm{1}$, respectiv în starea $\large\textrm{2}$. De exemplu,
$\large{\textrm{0}}\overset{0}{\longrightarrow}\large{\textrm{0}}\overset{0}{\longrightarrow}\large{\textrm{0}} \overset{1}{\longrightarrow}\large{\textrm{1}}\overset{1}{\longrightarrow}\large{\textrm{0}} \overset{0}{\longrightarrow}\large{\textrm{0}} \overset{1}{\longrightarrow}\large{\textrm{1}}\overset{1}{\longrightarrow}\large{\textrm{0}}\overset{0}{\longrightarrow}\large{\textrm{0}}$ produce octetul 000110110, cu valoarea 54 (deci un multiplu de 3).
Cât timp biții inițiali sunt nesemnificativi —constituind în fond reprezentări binare de câte o anumită lungime ale numărului 0 (care este multiplu de 3)— sistemul rămâne în starea inițială $\large\textrm{0}$. Când cuvântului binar existent în starea $\large\textrm{0}$ (asociată multiplilor de 3) i se alipește un bit 1, sistemul ajunge în starea $\large\textrm{1}$ (iar cuvântul format astfel reprezintă un număr care dă restul 1 la împărțirea prin 3).
Când cuvântului binar existent în starea $\large\textrm{1}$ (reprezentând deci, un număr de forma 3k+1) i se alipește un bit 0, sistemul ajunge în starea $\large\textrm{2}$; cuvântul format astfel reprezintă un număr care dă restul 2 la împărțirea prin 3 — fiindcă alipirea unui 0 corespunde înmulțirii cu baza de numerație, care este 2, iar 2*(3k+1) ≡ 2 mod 3.
Următorul tabel sintetizează explicația demarată mai sus, a funcționării sistemului:
| starea curentă | starea după alipire 0 | starea după alipire 1 |
| $\large\textrm{0}$ | $\large\textrm{0}$ (3k) | $\large\textrm{1}$ (3k+1) |
| $\large\textrm{1}$ | $\large\textrm{2}$ (2*(3k+1) ≡ 3k+2 (mod 3)) | $\large\textrm{0}$ (2*(3k+1)+1 ≡ 0 mod 3) |
| $\large\textrm{2}$ | $\large\textrm{1}$ (2*(3k+2) ≡ 1 mod 3) | $\large\textrm{2}$ (2*(3k+2)+1 ≡ 2 mod 3) |
Este clar acum că automatul reprodus mai sus produce (sau recunoaște, citind de pe o bandă de intrare) forma binară a oricărui număr natural și o clasifică modulo 3.
N.B.: automatul redat a servit ca exemplu în unele cărți de "limbaje formale și automate"; noi am evitat să fixăm o stare finală ($\large\textrm{0}$, în exemplele întâlnite), inducând instinctiv o valență de clasificare a cuvintelor (de fapt, nu greșeam dacă indicam drept finale toate cele trei stări — evitând să aveam vreo "noutate").
Apar următoarele chestiuni: să deducem expresia regulată corespunzătoare cuvintelor binare posibil de generat pentru o starea finală fixată; să redăm o modalitate adecvată pentru redarea grafică a automatului; să tratăm și cazul clasificării modulo 5 de exemplu (și poate, dar probabil prea ambițios, a cazului general modulo n, n≥2).
Caracterizarea binară regulată a multiplilor de 3
O expresie regulată descrie (sau generează) o anumită mulțime de cuvinte — un limbaj (anume, un "limbaj regulat"); se folosesc drept "operatori" principali două sau trei simboluri (externe alfabetului respectiv): | specifică o alegere alternativă de "litere", iar * specifică apariția de zero sau mai multe ori a literei; este adoptat de obicei și + pentru a specifica apariția cel puțin o dată, a literei. În plus se folosesc paranteze de grupare, extinzând la grupuri de simboluri, aplicarea operatorilor.
Obs. Mult peste conceptul de bază descris mai sus, modelarea și implementarea regexp a expresiilor regulate, existentă în diverse limbaje de programare, prevede și alți numeroși operatori, împreună cu fel de fel de facilități; și probabil nu degeaba, circulă "vorba": dacă vrei să rezolvi o problemă și implici "regexp", atunci… ai două probleme!
Pentru a formula expresia regulată asociată automatului redat mai sus, să considerăm deocamdată (sub)automatul constituit din stările $\large\textrm{0}$ (starea inițială) și $\large\textrm{1}$, fixând $\large\textrm{0}$ ca stare finală:
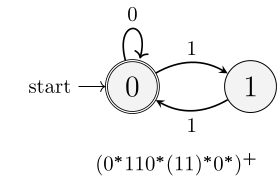
Starea $\large\textrm{0}$ acceptă introducerea unui bit 0 și fiind atât stare inițială cât și stare finală, rezultă că automatul produce (sau recunoaște) orice cuvânt binar format numai din cifre 0, iar mulțimea acestor cuvinte poate fi descrisă prin $0^*$; toate aceste cuvinte (mai puțin cuvântul nul, cu zero cifre 0, acoperit și acesta de șablonul "0*") reprezintă numărul zero și ele pot prefixa, ca "cifre nesemnificative" ale valorii numerice, oricare alt cuvânt produs de automat — încât este firesc să le ignorăm.
Starea $\large\textrm{0}$ acceptă însă un bit 1, conducând la starea $\large\textrm{1}$; aceasta acceptă și ea un bit 1, conducând la starea finală $\large\textrm{0}$; cuvântul generat astfel, într-o singură trecere, este 11 — dar putem repeta la nesfârșit și ținând seama că în starea $\large\textrm{0}$ putem intercala și oricâți biți 0, avem, pentru cuvintele produse, șablonul regulat $110^*(11)^*$; iar acest șablon se poate repeta (prin alipire la el însuși) la nesfârșit — dar fiindcă vrem să avem măcar un cuvânt asociat unui număr nenul, trebuie să folosim + , nu * și rezultă șablonul final $(110^{\boldsymbol{*}}(11)^{\boldsymbol{*}})^{\boldsymbol{+}}$.
Este ușor de demonstrat că orice cuvânt de această formă reprezintă un multiplu de 3: $(11)_2=3$, iar orice succesiune de $(11)$ echivalează cu o succesiune de cifre 3.
Aaa… am uitat că ajunși în starea $\large\textrm{0}$ putem alipi 0 (de zero sau mai multe ori); corectăm rezultatul "final" de mai sus: $(110^{\boldsymbol{*}}(11)^{\boldsymbol{*}}0^{\boldsymbol{*}})^{\boldsymbol{+}}$.
Completând raționamentul de mai sus pentru a viza și starea $\large\textrm{2}$, ajungem la următoarea formulare (pe care urmează să o demonstrăm):
Teoremă Forma binară a oricărui multiplu nenul al lui 3 este: $$\large((110^{\boldsymbol{*}}(11)^{\boldsymbol{*}}0^{\boldsymbol{*}})\,\boldsymbol{|}\,(1(01^{\boldsymbol{*}}0)^{\boldsymbol{+}}10^{\boldsymbol{*}}))^{\boldsymbol{+}}(11)^{\boldsymbol{*}} \qquad\qquad\qquad\normalsize{\boldsymbol{(1)}}$$
Demostrație
Fie $3n$ un multiplu nenul oarecare al lui 3. Pentru valori mici ale lui $n$, se verifică ușor că forma binară a lui $3n$ este de forma indicată: dacă în "110∗(11)∗0∗" considerăm zero pentru numărul de apariții dinaintea fiecărui operator '*' — obținem "11", care reprezintă 3 în baza 2; acceptând apariția unui singur 0, doar sub primul '*', rezultă "110", care are valoarea 6 (iar acceptând doi de '0' rezultă "1100", cu valoarea 12).
Apoi, 9 se obține din partea dreaptă a primului operator '|' din (1): "1001".
Să presupunem că $3n$ este de forma binară (1), pentru o valoare oarecare $n$; multiplul de 3 care îi urmează se obține adunându-i 3 (adică $11_2$).
Dacă $3n$ are la sfârșit "00", atunci adunându-i "11" se modifică numai acești ultimi doi biți ai lui $3n$; deci forma binară a lui $3n+3$ diferă de cea a lui $3n$ numai prin grupul ultimilor doi biți, deveniți $(11)$ — ceea ce corespunde ultimei părți din (1). Deci în acest caz, când $3n$ se încheie cu 00, ipoteza că $3n$ este de forma (1) asigură că și $3(n+1)$ este de forma (1).
Dacă $3n$ este de forma (1) și se încheie cu 01, atunci $3n$ se încheie neapărat conform parantezei din dreapta operatorului | din (1), cu "1(01∗0)+1" și avem acest calcul de adunare cu $3=11_2$ în baza 2:
1 01*0 01*0 ... 01*0 01*0 1 +
1 1
---------------------------
1 01*0 01*0 ... 01*0 10*0 0
Rezultatul fiind de forma "1(01∗0)+10*", deducem că și în acest caz, când $3n$ se termină cu 01, ipoteza că $3n$ este de forma (1) asigură că $3(n+1)$ este și el de forma (1).
Dacă $3n$ este de forma (1) și se încheie cu "10", atunci avem două subcazuri, după cum forma binară respectivă are la sfârșit una sau cealaltă dintre secvențele separate de '|' în (1). Pentru primul subcaz, avem două posibilități, după cum acceptăm sau nu cifre sau grupuri intermediare definite de '*':
11 00...00 11 11 11 0 +
1 1
---------------------
11 00...01 00 00 00 1
Rezultatul în acest sub-subcaz este de forma "110*1(00)*1" și el se regăsește în (1) ținând seama că ultimul operator '+' din (1) permite repetarea uneia sau alteia sau amândurora, dintre cele două paranteze operate în mijloc de '|': din prima paranteză reținem "110*" (putem ignora celelalte elemente, fiind sub '*') și adăugăm (în baza lui '+' menționat mai sus) din a doua paranteză "1(00)*1".
În al doilea sub-subcaz (eliminând cifrele zero intermediare), avem 11(11)*0 + 11 = 1(00)*1 și rezultatul este de forma din dreapta lui '|' din (1) (cu *=zero apariții).
Prin urmare, dacă $3n$ este de forma (1) și se încheie cu "10", atunci rezultă că și $3(n+1)$ este de forma (1).
Ne-a rămas cazul când $3n$ este de forma (1) și se încheie cu "11". Dacă $3n$ are forma "...110*(11)*", se vede imediat că adunându-i "11" se obține aceeași formă. În celălat sub-caz, avem ...1(01*0)+10*(11)* + 11 = ...1(01*0)+10*1(00)*10, rezultat care se regăsește în (1) repetând porțiunea "1(01*0)10*" (în baza operatorului final '+' din (1) și eliminând "1*").
Cu aceasta, teorema este demonstrată (conform principiului inducției matematice).
De observat că dacă în (1) adăugăm la sfârșit "00*", atunci (1) va exprima forma binară a oricărui multiplu nenul de 6 (multiplu de 3 încheiat cu zero, deci dublat — adică, multiplu de 6).
Asupra redării grafice a automatului
Într-un limbaj de programare, un automat ar fi reprezentat printr-un obiect de memorie conținând câmpuri pentru alfabetul de bază, pentru stările prevăzute și pentru tabelul de tranziții. Avem multe posibilități pentru a obține și o reprezentare grafică (de obicei folosim R cu pachetul igraph, sau uneori PostScript, Metapost, sau graphviz); dar probabil că cel mai bine este să folosim LaTeX: pachetul TikZ include și o bibliotecă automata, destinată reprezentării grafice a automatelor (și care este chiar ușor de folosit; v. An introduction to automata design with TikZ’s automata library). Am obținut imaginea grafică de automat redată la început, plecând de la următorul program LaTeX:
\documentclass{standalone} \usepackage{tikz} \usetikzlibrary{automata, arrows.meta, positioning} \begin{document} \begin{tikzpicture} [node distance = 2cm, on grid, auto, every state/.style = {font=\Large, fill=gray!10}] \node (0) [state, initial, initial text = {}] {$0$}; \node (1) [state, right = of 0] {$1$}; \node (2) [state, right = of 1] {$2$}; \path [-stealth, thick] (0) edge[loop above] node {0}() (0) edge[bend left] node[above] {1} (1) (1) edge[bend left] node[below] {1} (0) (1) edge[bend left] node[above] {0} (2) (2) edge[bend left] node[below] {0} (1) (2) edge[loop above] node {1}(); \end{tikzpicture} \end{document}
Sintaxa indicării unui arc, de exemplu de la nodul $\large{1}$ la nodul $\large{0}$, are această interpretare: trasează (aici curbat, nu drept) un arc de la marginea stângă a cercului care conține 1, la cercul care conține 0 și etichetează dedesubtul lui cu (bitul) 1.
După compilare (cu xelatex), am folosit programul pdftocairo, transformând fișierul PDF rezultat, în imaginea PNG redată la începutul acestui articol.
Limbajul binar al multiplilor de 5
Multiplii de 2, sau de 4 au o formă binară neinteresantă ("*0", respectiv "*00")…
Automatul care ne-ar permite să clasificăm formele binare după restul împărțirii la 5 are 5 stări, pe care le desemnăm după resturi; astfel, numărul asociat unei stări reprezintă modulo 5 chiar numărul a cărui formă binară a rezultat în starea respectivă (de exemplu, dacă N este numărul a cărui formă binară a rezultat în starea $\large{2}$ atunci avem N mod 5 = 2). Alegem $\large\textrm{0}$ drept stare inițială și totodată, drept stare finală.
Trecerea din starea $\large{s}$ în starea $\large{t}$ se face prin alipirea fie a unui bit '0', fie a unui bit '1', formei binare existente în starea $\large{s}$; fiindcă alipirea unui '0' înseamnă dublarea valorii numerice respective, rezultă că $\ \large{t}$ = (2$\large{s}$ + (fie 0, fie 1)) modulo 5 (de fapt… în loc de 5 putem avea oricare alt număr natural nenul).
Modelăm această formulă de trecere de la o stare la alta, într-un program R (incluzând tidyverse) și obținem tabelul tranzițiilor automatului:
Mod <- 5 # pentru stările "modulo 5" next_state <- function(state, bit) (2*state + bit) %% Mod tranz <- tibble(start = 0:Mod, dest_0 = next_state(start, 0), dest_1 = next_state(start, 1) ) %>% as.data.frame()
Obs. Numele "Mod" ales mai sus este cam nepotrivit: coincide cu numele funcției prevăzute în R pentru a calcula modulul unui număr complex…
Pentru tranzițiile modulo 5 tabelul tranz rezultat este:
start dest_0 dest_1
0 0 1
1 2 3
2 4 0
3 1 2
4 3 4
În acest tabel vedem de exemplu, acest ciclu: $\large{\textrm{0}}\overset{1}{\longrightarrow}\large{\textrm{1}}\overset{0}{\longrightarrow}\large{\textrm{2}}\overset{1}{\longrightarrow}\large{\textrm{0}}$ care înseamnă următorul lucru: dacă alipim '101' formei binare a unui multiplu de 5 (cum avem în starea $\large{\textrm{0}}$), atunci forma binară rezultată reprezintă deasemenea, un multiplu de 5 (ceea ce pare evident, ținând seama că $101_2=5$).
Dar mai general, pentru oricare ciclu din $\large{0}$ al grafului, dacă alipim succesiv formei binare existente în starea $\large{0}$, biții corespunzători arcelor acelui ciclu — atunci obținem în final o nouă formă binară, care și ea reprezintă un multiplu de 5; deci în principiu, putem determina expresia regulată asociată unui automat (și) plecând de la lista drumurilor (în cazul nostru, cicli) care unesc nodul de start cu nodul final.
Printr-un program LaTeX (cu TikZ) similar celui redat mai sus, avem această reprezentare vizuală a automatului definit mai sus:
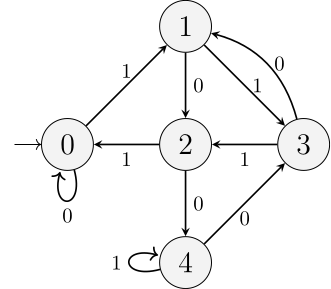
Ciclii acestui graf se văd "cu ochiul liber" (parcă n-ar mai fi necesar vreun program special). Mai sus am văzut deja un prim ciclu, iar expresia regulată asociată lui este 1010* (însemnând că alipirea acesteia — cu zero sau mai mulți biți 0 la sfârșit — formei binare din starea $\large{0}$, va păstra calitatea de multiplu de 5).
Din $\large{0}$ se ajunge în starea $\large{2}$ introducând fie biții 10, fie o secvență cu șablonul 11(01)*1 (buclând între stările $\large{1}$ și $\large{3}$); odată ajunși în starea $\large{2}$, se poate repeta la nesfârșit ciclul de stări $\large{2}-\large{4}-\large{3}-\large{2}$ (buclând eventual, în starea $\large{4}$).
Rezultă că toate ciclurile care pleacă din nodul $\large{0}$ se formează astfel: se emite un bit 1, ajungând în nodul $\large{1}$; de aici, există două alternative pentru a ajunge în starea $\large{2}$ (după cum se emite 0, respectiv 1); în final, din starea $\large{2}$ se emite 1, ajungând înapoi în starea $\large{0}$ (în care se poate bucla, emițând 0). Prin urmare avem:
Teoremă Forma binară a oricărui multiplu nenul al lui 5 este:
$\qquad\qquad$ 1((0$w$*) | (1(01)*1$w$*)) 10* $\quad$ unde $w$ = 01*0(01)*1 $\qquad\qquad\boldsymbol{(2)}$
Luând zero apariții pentru '*' și folosind una sau alta dintre cele două alternative din (2), regăsim de exemplu "101" (= 5) și "1111" (= 15… care este și multiplu de 3).
Intersecții…
Dacă împerechiem stările celor două automate considerate mai sus și "împerechiem" deasemenea, tabelele de tranziții ale acestora (de exemplu, starea (0, 0) trece în starea (1, 1) când se percepe un bit unu) — atunci automatul cu 15 stări care se obține este intersecția automatelor respective și ne-ar permite să generăm formele binare ale numerelor care sunt și multipli de 3 și multipli de 5. Desigur… nu este cazul să procedăm astfel: programul R redat mai sus ne permite (cu Mod = 15) să generăm direct tabelul de tranziții corespunzător automatului care ar clasifica modulo 15.
Dar scopul real (dacă nu vrem doar un nou "exemplu") nu este acela de a desena automatul-intersecție, ci de a evidenția cuvintele produse; în loc de a pleca de la automatul modulo 15, ar fi suficient (dar nu neapărat, mai simplu) să vedem care cuvinte binare pot fi exprimate atât în forma (1) (a cuvintelor generate de primul automat), cât și în forma (2) (limbajul celui de-al doilea automat).
Am observat deja mai sus, că "1111" (= 15) de exemplu, face parte din intersecția limbajelor exprimate prin (1) și (2) (confirmând că intersecția este nevidă); mai departe însă, a găsi direct forma generală a cuvintelor din intersecția celor două limbaje (bazându-ne numai pe expresiile regulate (1) și (2)), ne pare a fi extrem de complicat — așa că vom reveni la automatul modulo M (în particular, cu M=15).
vezi Cărţile mele (de programare)