Șabloanele binare ale multiplilor (II)
Un "automat binar modulo $M$" generează formele binare (peste alfabetul $\{0,1\}$) ale numerelor naturale, clasificându-le după resturile împărțirii la $M$; continuând [1] (unde $M$ era 3 sau 5), ne interesează limbajul generat pentru multiplii de $M$.
Ne poate interesa numai cazul când $M$ este impar: altfel, dacă $M=2^hR$ (unde $R$ este impar), atunci formele binare ale multiplilor de $M$ provin din cele ale multiplilor de $R$, adăugând la sfârșit $h$ biți '0'.
Asupra funcției de tranziție a automatului binar modulo M
Desemnăm stările prin resturile $0:(M-1)$ ale împărțirii la $M$ (cu $M\ge 3$); deci (v. [1]) din starea $s$ se trece în starea $t$ prin $\,t=2s+(0|1)\,\, (modulo\,M)$ (unde '$|$' alege fie '0', fie '1'). În loc să formulăm direct tabelul de tranziții (ca în [1]), să observăm că pentru $M=2K+1$ avem: dacă $s\le K$ atunci starea în care se trece la citirea unui bit '0' este $2s$ (fiindcă $t=2s\,(\boldsymbol{modulo}\,M)\boldsymbol{=}2s$, pentru $s\le K$), iar starea după citirea unui bit '1' este $2s+1$; iar pentru $K+1\le s \lt 2K+1$, vectorul tranzițiilor este fie $(1,3,5,\ldots,2K-1)$ (când se citește un bit '0'), fie $(2,4,\ldots,2K)$ (când se citește un bit '1').
Prin urmare, în loc de "tabelul tranzițiilor" este suficient să considerăm vectorii $T^0=(0, 2, 4, \ldots, 2K, 1, 3, 5, \ldots, 2K-1)$ și $T^1=(1, 3, 5, \ldots, 2K-1, 0, 2, 4, \ldots, 2K)$; pentru orice stare $s$, avem fie $t=T^0[s]$, fie $t=T^1[s]$ după cum în starea $s$ se preia un bit 0, respectiv un bit 1 și invers: dacă știm că din starea $s$ s-a trecut în starea $t$, atunci bitul citit pentru aceasta a fost 0 dacă $t$ apare pe locul $s$ în vectorul $T^0$ și a fost 1 dacă $t$ apare pe locul $s$ în vectorul $T^1$.
În R, lucrurile pot fi modelate astfel (pentru $M$ impar, indicat):
M <- 15L pare <- seq(0L, M, by=2L) # numerele pare de sub M ipar <- seq(1L, M-1L, by=2L) # impare mai mici ca M T0 <- c(pare, ipar) T1 <- c(ipar, pare) bit_from_to <- function(s, t) { if(t == T0[s+1]) return(0) if(t == T1[s+1]) return(1) }
$t$ trebuie căutat pe locul s+1 (nu s), fiindcă (în R) vectorii sunt indexați de la 1 (și nu de la zero). Dacă din starea s nu se poate trece (direct) în starea t, atunci bit_from_to(s, t) returnează (implicit) NULL; altfel, returnează 0 sau 1, după cum valoarea t apare pe locul s+1 în vectorul T0, respectiv în vectorul T1.
Dacă nodul t este accesibil din nodul s, dar nu direct ci printr-un număr de stări intermediare, atunci iterând bit_from_to() pe nodurile drumului respectiv, vom obține cuvântul binar care duce din s în t.
Graful automatului modulo M (cu M impar)
Îmbinând vectorii T0 și T1, obținem matricea arcelor s --> t ale automatului respectiv:
library(tidyverse) # din care avem de exemplu, operatorul '%>%' Edg <- rbind(rbind(0:(2*k), T0) %>% t(), rbind(0:(2*k), T1) %>% t() ) %>% apply(., 2, as.character)
Dar nu vom folosi Edg decât pentru a defini graful corespunzător nodurilor și arcelor respective, după ce includem pachetul igraph:
library(igraph) Atm <- graph_from_edgelist(Edg) > Atm IGRAPH 036690d DN-- 15 30 -- + attr: name (v/c) + edges from 036690d (vertex names): [1] 0 ->0 1 ->2 2 ->4 3 ->6 4 ->8 5 ->10 6 ->12 7 ->14 8 ->1 9 ->3 [11] 10->5 11->7 12->9 13->11 14->13 0 ->1 1 ->3 2 ->5 3 ->7 4 ->9 [21] 5 ->11 6 ->13 7 ->0 8 ->2 9 ->4 10->6 11->8 12->10 13->12 14->14
În mod implicit, nodurile grafului sunt desemnate prin 1, 2, etc. (plecând de la 1, nu de la 0); dar fiindcă am avut grijă să transformăm valorile din matricea Edg în valori de tip character, graph_from_edgelist() a adăugat nodurilor atributul "name" (permițând și nodul 0, ca fiind nodul cu numele "0").
Dacă vrem, deși nu ne ajută cu nimic (fiind totuși un sprijin vizual, din când în când), putem plota imediat graful rezultat (de exemplu, pentru $M$=15):
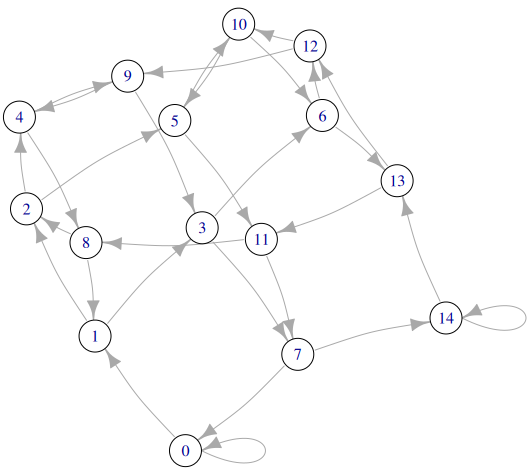
Unele cicluri (mai scurte) se văd ușor, de exemplu (0, 1, 3, 7, 0); aplicând bit_from_to() primelor două vârfuri din ciclu, următoarelor două, ș.a.m.d., obținem cuvântul binar corespunzător ciclului, "1111" — ceea ce înseamnă (v. [1]) că alipind acest cuvânt formei binare existente în starea 0, rezultă o formă binară specifică deasemenea, stării 0; altfel spus (dar este evident), adăugând unui multiplu de 15 valoarea 11112 = 15, rezultă tot un multiplu de 15.
Următoarea funcție returnează cuvântul binar corespunzător ciclului dat:
cycle_to_bin <- function(Cy) sapply(1:(length(Cy)-1), function(i) bit_from_to(Cy[i], Cy[i+1]))
De exemplu, invocând cycle_to_bin(Cy) pentru ciclul Cy = c(1, 2, 5, 11, 8, 1) obținem "01110" — însemnând că alipirea acestui cuvânt binar (a cărui valoare este 14) formei binare existente în starea "1" păstrează restul 1 la împărțirea prin 15.
Ciclurile grafului Atm
Un ciclu oarecare (orientat, în cazul nostru) se poate construi independent (ca obiect IGRAPH), prin funcția graph.ring() (deci un "ring" este o anumită structură de date care include și un vector de vârfuri adiacente din aproape în aproape); de exemplu:
> graph.ring(5, directed = TRUE) IGRAPH 0c72116 D--- 5 5 -- Ring graph + attr: name (g/c), mutual (g/l), circular (g/l) + edges from 0c72116: [1] 1->2 2->3 3->4 4->5 5->1 # ciclul (1,2,3,4,5,1)
Ciclurile unui graf sunt acele subgrafuri care sunt izomorfe unui "ring" (idee preluată din https://lists.nongnu.org/archive/html/igraph-help/2009-04/msg00125.html):
find_cycles <- function(G, h) { # ciclii de lungime h+1 ai grafului G ring <- graph.ring(h, directed=TRUE) subgraph_isomorphisms(ring, G) }
Un ciclu al grafului G este într-adevăr, un subgraf al lui G…
subgraph_isomorphisms() consideră un graf-"ring" independent de G și produce toate bijecțiile care păstrează adiacența între vârfurile acestui ring și cele ale unui subgraf (cu același număr de vârfuri ca și ring-ul) al lui G — ceea ce înseamnă, în primul rând, că pentru un ciclu al lui G vor rezulta mai multe liste de vârfuri; de exemplu, pentru ciclul cu vârfurile "2", "4", "8" vor rezulta trei "subgrafuri" izomorfe, dat fiind că acest ciclu poate pleca din "2", sau din "4", sau din "8".
În al doilea rând, nu poate fi vorba decât de cicluri simple (dacă s-ar repeta vreun vârf, atunci n-am mai avea "bijecție"); iar în cazul de față, acest fapt s-ar putea să ne încurce, la un moment dat (cum vom vedea mai târziu).
Ciclurile grafului Atm au cel mult $2M$ arce și le putem obține (ca "subgrafuri") invocând find_cycles() (pentru fiecare lungime ≥ 3, posibilă):
Lcy <- lapply(2:(2*M), find_cycles, G = Atm) %>% compact() # elimină subgrafurile NULL (nu avem cicluri foarte lungi)
Lista Lcy asociază lungimii indicate, lista subgrafurilor (dacă există) reprezentând ciclii de lungimea respectivă. Mai precis… pentru fiecare lungime h a unui ciclu existent în G, Lcy[[h]] este o listă care are ca elemente câte o listă pentru fiecare subgraf izomorf ciclului respectiv, listă care conține unele informații extrase din obiectul IGRAPH corespunzător subgrafului (între care și numele de vârfuri prevăzute în G), împreună cu un vector care conține vârfurile asociate în G prin izomorfism (și numite ca în G).
De exemplu (cu $M$=15), pentru ciclii cu 3 vârfuri avem:
> Lcy[[2]]
[[1]] + 3/15 vertices, named, from 8491ae6: [1] 2 4 8 # ciclul (2,4,8,2)
[[2]] + 3/15 vertices, named, from 8491ae6: [1] 4 8 2
[[3]] + 3/15 vertices, named, from 8491ae6: [1] 6 12 10 # ciclul (6,12,10,6)
[[4]] + 3/15 vertices, named, from 8491ae6: [1] 8 2 4
[[5]] + 3/15 vertices, named, from 8491ae6: [1] 10 6 12
[[6]] + 3/15 vertices, named, from 8491ae6: [1] 12 10 6
Folosindu-ne de faptul că aceste subliste memorează și numele de vârfuri din G, putem viza numai ceea ce ne interesează, anume vectorul vârfurilor ciclului respectiv:
> names(Lcy[[2]][[3]]) [1] "6" "12" "10" # ar fi de adăugat "6", pentru a încheia ciclul
Putem elimina primul nivel de imbricare (desemnat mai sus prin 'h') al listei Lcy — folosind unlist() cu opțiunea recursive=FALSE; apoi, prin lapply() putem aplica names() fiecăreia dintre listele rămase astfel direct sub Lcy — obținând ca vectori, toate ciclurile lui G (de lungime ≥ 3, cu observația că fiecare ciclu apare de mai multe ori, după cum începe dintr-unul sau altul dintre nodurile sale).
Însă nu toate ciclurile ne interesează… Iar unele cicluri care probabil că ne-ar interesa, nu vor fi obținute astfel, nefiind cicluri simple.
Cuvintele de bază pentru formele binare ale multiplilor
Multiplilor de $M$ (și exemplificăm iarăși cu $M$ = 15) le corespund ciclii care pleacă din starea "0"; deci ne interesează ciclii care pleacă din "0" (și vom adăuga "0" la sfârșit). Folosind cum avansasem mai sus unlist(), lapply() și names(), constituim lista M0 a tuturor acestor cicli (ca vectori de integer):
Lcy <- unlist(Lcy, recursive = FALSE) M0 <- lapply(Lcy, function(Cy) { nm <- names(Cy) if(nm[[1]] == "0") return(c(nm, "0") %>% as.integer()) }) %>% compact() > M0 [[1]] [1] 0 1 3 7 0 [[2]] [1] 0 1 2 5 11 7 0 [[3]] [1] 0 1 3 6 13 11 7 0 [[4]] [1] 0 1 2 4 9 3 7 0 [[5]] [1] 0 1 3 6 12 10 5 11 7 0 [[6]] [1] 0 1 2 5 10 6 13 11 7 0 [[7]] [1] 0 1 3 6 13 12 10 5 11 7 0 [[8]] [1] 0 1 2 5 10 6 12 9 3 7 0 [[9]] [1] 0 1 2 4 9 3 6 13 11 7 0 [[10]] [1] 0 1 2 5 10 6 13 12 9 3 7 0 [[11]] [1] 0 1 3 6 12 9 4 8 2 5 11 7 0 [[12]] [1] 0 1 2 4 9 3 6 12 10 5 11 7 0 [[13]] [1] 0 1 3 6 13 12 9 4 8 2 5 11 7 0 [[14]] [1] 0 1 2 4 9 3 6 13 12 10 5 11 7 0
Fiecăruia dintre aceste 14 cicluri, îi corespunde prin funcția cycle_to_bin() câte un cuvânt binar care, alipit formei binare existente în starea "0", nu modifică proprietatea de "multiplu de $M$" a acesteia. De fapt… cycle_to_bin() nu produce cuvânt (cum ar fi trebuit), ci un vector integer; corectăm ad-hoc, folosind paste():
Bin <- lapply(M0, cycle_to_bin) %>% sapply(., function(VB) paste0(as.character(VB), collapse="")) %>% sort() for(i in 1:length(Bin)) cat(i, ". \"", Bin[i], "\"\n", sep="") 1. "100100010101" 2. "1001001001" 3. "1001001110101" 4. "1001011" 5. "1010100011" 6. "101011001" 7. "10101110011" 8. "101101" 9. "110001011101" 10. "110010101" 11. "1101001" 12. "1101101011101" 13. "1101110101" 14. "1111"
Ne putem și încredința, că valorile numerice ale cuvintelor din Bin sunt multipli de 15 (cel mai simplu (că în R nu dispunem direct de conversie din binar în zecimal), ar fi să ducem Bin în Python, ca listă-Python de șiruri, folosind apoi int(Bin[i], 2) % 15) — ceea ce înseamnă că dacă vom alipi oricare dintre cuvintele respective, formei binare constituite în starea "0", forma binară rezultată va reprezenta și ea, un multiplu de 15.
O expresie binară regulată pentru multiplii de 15
Plecând de la cele 14 cuvinte "de bază" din Bin, putem formula o expresie regulată a formelor binare ale multiplilor de 15, dacă ținem seama de următoarele aspecte (care se pot vedea imediat și pe graful redat mai sus): în stările "0" și respectiv "14" putem alipi oricâți biți 0, respectiv 1; între stările "4" și "9", respectiv "5" și "10" se poate intercala de oricâte ori secvența de doi biți "11", respectiv "00".
În plus, putem concatena (în particular, putem repeta) oricare dintre cuvintele respective, rezultând forme binare care alipite celeia din starea "0", păstrează proprietatea acestei stări de a reprezenta binar, multiplii de 15.
Probabil, nu va fi cea mai concisă expresie regulată, dar este una (de plecare); probabil că nu va fi nici completă, dat fiind că am vizat numai ciclurile simple…
Avem deci de montat în anumite locuri, operatorii regulați '*' și '|' (de exemplu, cuvântului Bin[14] îi vom asocia expresia regulată "11110*"). Dar pentru a determina locurile din cuvânt în care ar trebui să intercalăm '*', trebuie să considerăm nu numai cuvântul respectiv (din Bin), dar și ciclul din care a provenit… Prin urmare, să reconstruim "Bin", adăugând acum și ciclurile corespunzătoare cuvintelor:
CB <- lapply(M0, function(VB) c(paste(VB, collapse = " "), paste0(as.character(cycle_to_bin(VB)), collapse = "")) ) Bin <- Reduce(rbind, CB) colnames(Bin) <- c("cycle", "binword") rownames(Bin) <- NULL > Bin cycle binword [1,] "0 1 3 7 0" "1111" [2,] "0 1 2 5 11 7 0" "101101" [3,] "0 1 3 6 13 11 7 0" "1101001" [4,] "0 1 2 4 9 3 7 0" "1001011" # 1001(11)*0110* [5,] "0 1 3 6 12 10 5 11 7 0" "110010101" [6,] "0 1 2 5 10 6 13 11 7 0" "101011001" [7,] "0 1 3 6 13 12 10 5 11 7 0" "1101110101" [8,] "0 1 2 5 10 6 12 9 3 7 0" "1010100011" [9,] "0 1 2 4 9 3 6 13 11 7 0" "1001001001" [10,] "0 1 2 5 10 6 13 12 9 3 7 0" "10101110011" [11,] "0 1 3 6 12 9 4 8 2 5 11 7 0" "110001011101" [12,] "0 1 2 4 9 3 6 12 10 5 11 7 0" "100100010101" # 1001(11)*00010(00)*1010* [13,] "0 1 3 6 13 12 9 4 8 2 5 11 7 0" "1101101011101" [14,] "0 1 2 4 9 3 6 13 12 10 5 11 7 0" "1001001110101"
Să observăm că oricare ciclu din Bin de rang ≥ 4, conține (într-o ordine de trecere sau alta) fie nodurile 4 și 9, fie nodurile 5 și 10; în locul asociat în cuvântul binar, va trebui să înlocuim "1" (respectiv "0") cu secvența regulată "1(11)*" (respectiv "0(00)*").
De exemplu, în Bin[4, 1] avem "0 1 2 4 9 3 7 0"; trecerii (4, 9) îi corespunde locul 4 din șirul Bin[4,2] — deci expresia regulată pe care trebuie să o avem în vedere este "1001(11)*011" (sau, mai bine: "1001(11)*0110*").
Pentru cuvântul de la rangul 12, trebuie să intercalăm pe locurile 5 și 10, rezultând expresia regulată "1001(11)*00010(00)*1010*".
Dar… să observăm că există un nod (unul singur) care nu apare nicăieri în coloana "cycle" — anume, 14; cu alte cuvinte… forma binară a unui multiplu de 15 nu ar putea fi prelungită încât să reprezinte un număr care să dea restul 14 la împărțirea prin 15 (și care să fie prelungită în continuare până ce rezultă iarăși un multiplu de 15) — ceea ce este cu siguranță, fals.
Pe graful redat mai sus vedem că există un ciclu care pleacă din "0" și trece prin nodul "14", de exemplu: "0 1 3 6 13 11 7 14 13 12 9 3 7 0" — numai că acesta nu este un ciclu simplu (trece de două ori prin nodurile 3, 13 și 7), încât a fost ignorat de către subgraph_isomorphisms().
Aplicând cycle_to_bin() ciclului menționat, obținem "1 1 0 1 0 0 0 0 1 0 0 1 1" și ar trebui să considerăm (pe lângă cele 14 cuvinte binare "de bază" obținute mai sus) și cuvântul "1101000010011" (am marcat bitul de trecere din starea 7 în starea 14), de unde expresia regulată "11010001*010011" (în starea 14 se pot emite oricâți biți 1, rămânând în starea 14); se poate constata ușor că această expresie nu derivează prin concatenare, din cuvinte înregistrate în Bin — încât ea trebuie adăugată celor "de bază" (care și ele, nu provin una din altele, prin concatenare).
Alipind prin '|' toate cele 15 expresii regulate asociate cum am arătat mai sus cuvintelor "de bază", obținem o expresie regulată care caracterizează toate formele binare ale multiplilor de 15… Ar fi de dorit desigur, o demonstrație (sau poate, un contraexemplu); ar fi de demonstrat că oricare multiplu de 15 are ca formă binară, sau unul dintre cele 15 cuvinte evidențiate mai sus, sau o compunere (concatenare) a unora dintre acestea.
vezi Cărţile mele (de programare)