Testare, măsurare şi sumarizare (III)
[1] "myProgram" pentru Sudoku, pas cu pas
[2] Testare, măsurare şi sumarizare (I, II)
Demarăm unele investigaţii pe setul de grile Sudoku „dificile” considerat în [2]:
# explore1.R library(tidyverse) str2vec <- function(str) # "şir de caractere" ==> vectorul caracterelor unlist(strsplit(str, split=NULL, perl=TRUE)) print.grila <- function(grila, zero=FALSE) { G <- str2vec(grila) if(zero) G[G == "."] <- "0" dim(G) <- c(9, 9) # structurează ca matrice 9(coloane) × 9(linii) print.table(t(G)) # afişează fără '"' (nu "2", ci 2), pe linii } n.clues <- function(grila) { # numărul de valori 1..9 fixate iniţial G <- str2vec(grila) length(G[G != "."]) } HG <- readRDS("HG.rds") # 478 de grile Sudoku "dificile"
HG$grid înregistrează grilele iniţiale, iar HG$sol – soluţiile acestora; pe coloana HG$back avem o listă de câte 50 de valori întregi, reprezentând fiecare numărul de reveniri pe parcursul soluţionării repetate a grilei respective, prin programul su_doku.R din [1].
În principiu, asimilăm „dificultatea” grilei cu media valorilor back asociate ei (durata soluţionării grilei depinde liniar de back).
Formulările mai complicate sau mai lungi le vom înscrie în fişierul "explore1.R"; pentru liniile mai simple (ca şi în scopul verificării unor aspecte), folosim consola interactivă R (liniile respective încep cu prompt-ul obişnuit, ">").
Repartiţia după numărul de indicii iniţiale
Se ştie că pentru ca o grilă Sudoku să aibă soluţie unică este necesar ca valorile fixate iniţial să fie în număr de cel puţin 17 şi măcar 8 dintre acestea să fie distincte.
Să adăugăm în tabelul HG (obiect al clasei tibble") o coloană conţinând pentru fiecare grilă, numărul de indicii iniţiale:
HG <- HG %>% mutate(clues = unlist(lapply(grid, n.clues))) %>% relocate(clues, .after = 1)
> head(HG, 2) # verificare # A tibble: 2 x 4 grid clues sol back <chr> <int> <chr> <list> 1 85...24..72......9..4.........1… 22 8596124377238541691643795289861… <int … 2 ..53.....8......2..7..1.5..4...… 23 1453276988396541276729185434961… <int …
Numărul valorilor indicate iniţial spune ceva şi despre „dificultate” (dacă se dau mai mult de 40 de valori, atunci grila respectivă devine „uşoară”). Putem vedea în mai multe moduri, cam cum stau lucrurile pentru grilele din HG:
> (table(HG[c("clues")]) -> vcl) 17 19 20 21 22 23 24 25 26 28 38 2 2 96 195 118 16 7 2 2 > round(vcl/sum(vcl), 3) 17 19 20 21 22 23 24 25 26 28 0.079 0.004 0.004 0.201 0.408 0.247 0.033 0.015 0.004 0.004 > hist(HG$clues)
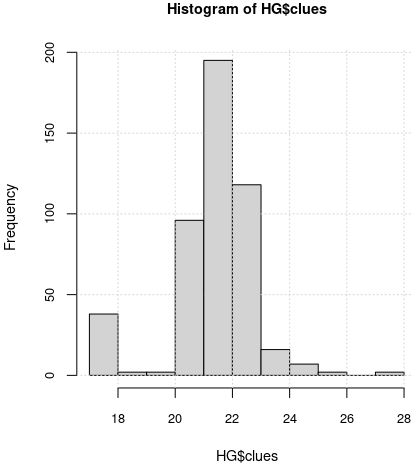
Cam 8% dintre grile au câte 17 indicii, 3% au câte 24, iar 85% sunt grile cu 22, 23 sau 21 de indicii (dintre care aproape jumătate sunt cu câte 22 indicii).
Evidenţierea grilelor cu o aceeaşi soluţie
Există grile iniţiale care au o aceeaşi soluţie finală:
> unique(HG$sol) %>% length [1] 428 # deci 478 - 428 = 50 alte grile au soluţia între soluţiile acestor 428
Cu alte cuvinte, există 428 de grupuri de grile, fiecare conţinând fie una singură, fie două sau mai multe grile – caz în care grilele din grupul respectiv au o aceeaşi soluţie. Ca să clarificăm lucrurile, putem folosi funcţiile implicate de group_by():
> grs <- HG %>% group_by(sol) > grs %>% count(sol) %>% filter(n > 1) %>% arrange(desc(n)) # A tibble: 30 x 2 # 30 grupuri au câte măcar două grile # Groups: sol [30] sol n <chr> <int> 1 1234567894571892369683271542495618735769384128317426953142759686958143… 12 2 1234567894571892368693271542718459633846925176957318425129643787362184… 5 3 1234967854572819369683571422491658735769384218317426593145792686958243… 5 4 1234567894567891237891325462648739513179258648956412375723946186382174… 3 5 1234567894567891237982135642375486915193628478641973523428759166759214… 3 6 1234567894571892366892734152943685717615243988359176423426918575187329… 3 7 1234567894571892636892374152415783967956138248369245713128956475687419… 3 8 1234567894567891237891325642678943513182754965943618726459182378726439… 2 9 1234567894567891237891325642753614983418952769682473155976138426145289… 2 10 1234567894567891237891325642789456313156274989643182755928613476375948… 2 # … with 20 more rows
Deci există 12 grile care au o aceeaşi soluţie, două grupuri pentru care cele câte 5 grile conţinute au aceeaşi soluţie, ş.a.m.d. Să determinăm liniile din tabelul HG pe care se află cele 12 grile cu aceeaşi soluţie:
> lgr <- group_rows(grs) > ( i12 <- lgr[order(sapply(lgr, length), decreasing=TRUE)][[1]] ) [1] 344 345 346 359 360 361 363 402 429 461 465 467
group_rows() a produs lista lgr de vectori întregi care dau indecşii rândurilor din tabelul HG corespunzătoare fiecăruia dintre grupurile care au fost ataşate prin group_by() acestui tabel; ordonând lgr descrescător după lungimile vectorilor conţinuţi, am găsit pe primul loc vectorul indecşilor liniilor corespunzătoare celor 12 grile cu aceeaşi valoare în câmpul $sol.
Să afişăm cele 12 linii; excludem câmpul $sol (care are aceeaşi valoare pe toate liniile) şi simplificăm (într-o nouă coloană) câmpul $grid, eliminând caracterul '.' (rămân numai valorile 1..9 care au fost fixate iniţial, ceea ce este suficient în general, pentru a putea sesiza mici deosebiri între cele 12 grile iniţiale); adăugăm coloana $back1 pe care înscriem media celor câte 50 de valori asociate în lista $back fiecărei grile:
> HG12 <- HG[i12, ] %>% + select(grid, clues, back) %>% + mutate(grid1 = str_replace_all(grid, "\\.", ""), + back1 = round(unlist(lapply(.$back, mean)))) %>% + arrange(desc(back1)) > print(HG12 %>% select(grid1, clues, back1)) # A tibble: 12 x 3 grid1 clues back1 <chr> <int> <dbl> 1 3483681467392547686765 22 845 2 3483683146739254768675 22 710 3 3483681467394254768675 22 678 4 3483681467392547686475 22 529 5 3448368146739254768675 22 514 6 3483681467397254768675 22 506 7 3483681467392576864754 22 435 8 3483681446739254768675 22 327 9 3483681467391247686475 22 322 10 3483681467391247686765 22 245 11 3483683146739124768675 22 245 12 3483681467391247686735 22 159
Cele 12 grile (cu o aceeaşi soluţie) au un acelaşi număr (22) de indicii. Pe coloana $grid1 putem sesiza uşor mici diferenţe între grilele respective, iar acestea au implicat o variaţie importantă (de la 159 la 845) a valorilor parametrului back1. Să afişăm de exemplu, primele două grile – dar în ordine inversă:
> for(i in 2:1) print.grila(HG12$grid[i]) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] . . 3 . . . . . . [2,] 4 . . . 8 . . 3 6 [3,] . . 8 3 . . 1 . . [4,] . 4 . . 6 . . 7 3 [5,] . . . 9 . . . . . [6,] . . . . . 2 . . 5 [7,] . . 4 . 7 . . 6 8 [8,] 6 . . . . . . . . [9,] 7 . . . . . 5 . . [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] . . 3 . . . . . . [2,] 4 . . . 8 . . 3 6 [3,] . . 8 . . . 1 . . [4,] . 4 . . 6 . . 7 3 [5,] . . . 9 . . . . . [6,] . . . . . 2 . . 5 [7,] . . 4 . 7 . . 6 8 [8,] 6 . . . . . . . . [9,] 7 . . 6 . . 5 . .
Singura diferenţă între acestea apare în coloana a 4-a: în loc de "3" pe al treilea loc, pe cealaltă grilă avem "6", în ultima poziţie; „dificultatea” obţinerii soluţiei (aceeaşi soluţie, pentru ambele grile) a crescut astfel, de la 710 la 845.
Sumarizarea dificultăţii grilelor
Mai sus am înfiinţat (de la consolă) coloana $back1 numai pentru HG12; să o adăugăm întregului set, în "explore1.R" (de data aceasta, cu valori int, în loc de dbl):
HG$back1 <- as.integer(round(unlist(lapply(HG$back, mean))))
Prin summary avem o caracterizare imediată a repartizării după valorile $back1 a celor 478 de grile din HG:
> summary(HG$back1) Min. 1st Qu. Median Mean 3rd Qu. Max. 0.00 51.25 111.50 145.53 183.00 845.00
Cam câte 25% dintre grilele respective au "back1" cel mult 51.25 (am zice că sunt relativ „uşoare”), respectiv cel puţin 183 (iar pentru celelalte 50%, "back1" este între 51.25 şi 183). Cam 50% dintre grile au valoarea "back1" la stânga (iar celelalte 50%, la dreapta) valorii mediane 111.50; media 145.53 fiind sensibil mai mare ca mediana, avem la dreapta medianei şi valori cam „exagerat” de mari ("outliers", corespunzător aici unor grile foarte „dificile”).
Pentru grilele cu dificultatea "back1" mai mare ca 200, avem:
> hard <- HG %>% filter(back1 > 200) %>% select(-back) %>% arrange(desc(back1)) > hist(hard$back1, cex.lab=0.9, cex.main=0.9, cex.axis=0.8); grid()
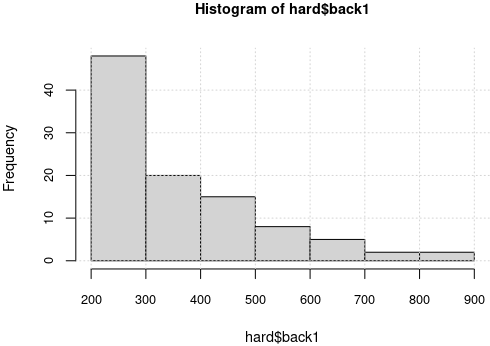
nrow(hard) ne arată că avem exact 100 astfel de grile, iar de pe histograma obţinută vedem că dintre acestea cam 50 au "back1" între 200 şi 300, vreo 20 au "back1" între 300 şi 400, etc.; numai vreo 4 grile au „dificultatea” cea mai mare, între 700 şi 900.
Pentru a sintetiza grafic repartiţia grilelor, după variabilele $clues şi $back1, putem considera de exemplu această funcţie (dar sunt multe alte posibilităţi):
back_clues <- function(dataSet = HG) { boxplot(back1 ~ clues, data = dataSet, cex = 0, cex.lab=0.9, cex.main=0.9, cex.axis=0.8, lwd=1.5) stripchart(back1 ~ clues, data = dataSet, method = "jitter", pch=20, cex=0.7, col = 2:12, vertical=TRUE, add=TRUE) grid() }
Precizăm doar că method="jitter" deplasează puţin punctele, pentru a evita cumva suprapunerile (altfel, presupunem că se ştie: help(nume_funcţie), de exemplu help(stripchart), afişează informaţiile necesare despre funcţia respectivă, inclusiv exemple de folosire).
Pentru întregul set HG, apelând deci back_clues(), avem:
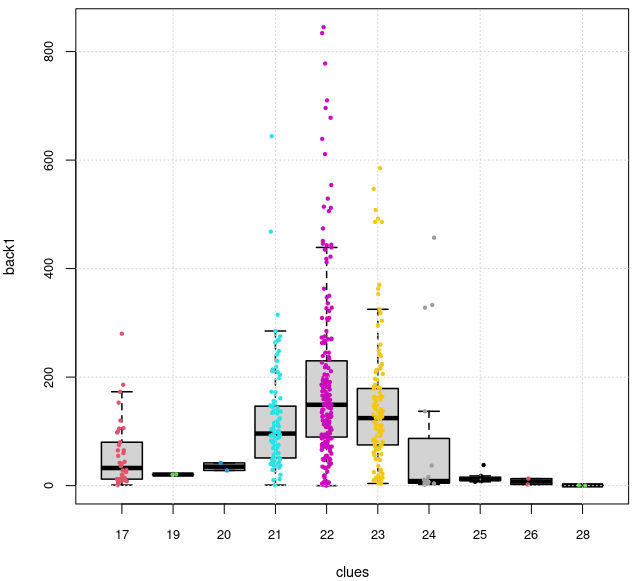
În baza acestei imagini, putem considera că relevante ca „dificultate” sunt numai grilele (şi de fapt, numai câte o parte a acestora) cu 17, 21, 22, 23 sau 24 indicii iniţiale; pentru celelalte, avem numai valori foarte mici pentru $back1 şi le putem considera ca fiind „uşoare” (cel mai uşoare fiind cele cu 28 indicii, apoi cele cu câte 26 sau 19 indicii, apoi cele cu 25 sau cu 20 indicii).
Selectând numai grilele între care sunt şi cele dificile, avem:
> back_clues(HG %>% filter(clues %in% c(17, 21, 22, 23, 24)))
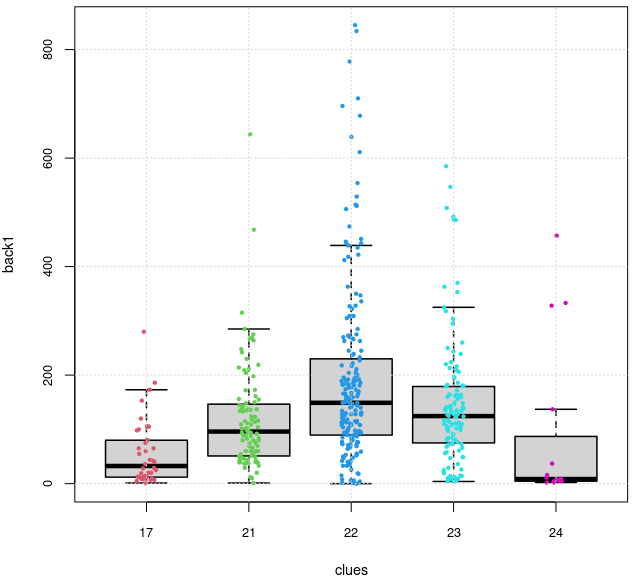
Se vede că avem puţine grile care sunt într-adevăr, „dificile”: deasupra ordonatei 450 avem numai vreo 25 de puncte.
Următoarea funcţie afişează grila cea mai dificilă, dintre cele cu acelaşi număr de indicii:
theHarder <- function(nclues) { hg <- HG %>% filter(clues == nclues) %>% filter(back1 == max(back1)) print.grila(hg$grid[1]) hg # returnează obiectul "tibble" corespunzător grilei afişate }
Am afişat deja mai sus, cel mai dificile două grile (cu câte 22 indicii, având back1 845 şi respectiv 710); să afişăm grila cea mai dificilă dintre cele cu câte 21 de indicii (ordonata punctului corespunzător ei pe imaginea redată mai sus este ceva mai mare ca 600):
> theHarder(21) [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [1,] . . . . 9 . . 5 . [2,] . 1 . . . . . 3 . [3,] . . 2 3 . . 7 . . [4,] . . 4 5 . . . 7 . [5,] 8 . . . . . 2 . . [6,] . . . . . 6 4 . . [7,] . 9 . . 1 . . . . [8,] . 8 . . 6 . . . . [9,] . . 5 4 . . . . 7 # A tibble: 1 x 5 grid clues sol back back1 1 ....9..5..1.....3...23..7...… 21 7438921565186479329623517486… <int … 644
Desigur, prin:
> lapply(c(17, 21, 22, 23, 24), theHarder) -> lstH
vom obţine pe ecran cele 5 cel mai dificile grile dintre cele cu numărul respectiv de indicii, obţinând şi o listă lstH a obiectelor "tibble" asociate acestora.
vezi Cărţile mele (de programare)