Achiziţii matematice şi creaţie grafică (I)
Chiar şi o experienţă modestă ca aceea din [1] sugerează măcar, că matematica este cheia înţelegerii rezultatelor obţinute prin programe de "creaţie grafică". Pe de altă parte (şi cumva "invers"), putem crea mereu programe prin care să experimentăm grafic anumite fapte de matematică elementară - sprijinind înţelegerea acestora şi poate, creând premisele implicării lor în elaborarea de "creaţii grafice" (angajând un program adecvat).
Ne propunem aici să creem un program R prin care să ilustrăm proprietăţi ale transformării z −> z2, unde z reprezintă punctele unui anumit domeniu din planul complex; vizăm în principal aceste trei cazuri: z parcurge fie o dreaptă orizontală, fie una verticală, fie interiorul unui dreptunghi cu baza paralelă axei reale. O "implicare" imediată ar fi aceasta: ce obţinem aplicând asemenea transformări (poate şi "la a 3-a", nu doar la pătrat) tablei de şah create în [2]?
1. Elaborarea programului de vizualizare a transformării
La prima vedere, constituirea programului pare banală: iei z "de aici până aici" cu un anumit pas şi plotezi punctele z2… Totuşi, constituirea programului decurge în mod firesc în mai multe etape succesive şi uneori avem de ales între două variante, iar alegerea făcută la un anumit moment poate avea consecinţe neprevăzute (inclusiv, binecunoscutul regret: "A... mai bine alegeam cealaltă variantă de lucru!").
Ne gândim întâi la o funcţie care să returneze o reţea de puncte (ca numere complexe) ale unui astfel de domeniu (orizontal, vertical sau dreptunghiular) şi imaginăm acest prototip:
build_mesh <- function(bltr, pass=0.1, value, direction)
'bltr' trebuie să fie un vector cu două sau cu patru valori numerice (reale), indicând capetele unui segment orizontal sau vertical în primul caz, respectiv coordonatele a două vârfuri opuse ale unui dreptunghi (anume "bottom-left" şi "top-right" - sugerate prin denumirea "bltr"). De exemplu, pentru cazul vectorului (1, 3), cu direction = 2 şi value = 5 (adică, segment vertical la abscisa 5) - va trebui returnat un vector de numere complexe de forma 5 + t i, unde t parcurge cu pasul indicat în parametrul 'pass' intervalul [1, 3].
Optăm pentru următoarea implementare, în care ţinem seama de faptul că 'value' şi 'direction' sunt necesari numai pentru segmente (nu şi pentru cazul dreptunghiurilor) şi în plus, de situaţia în care 'value' ar conţine eventual mai multe valori:
build_mesh <- function(bltr, pass=0.1, value=NULL, direction=NULL) { Z <- as.complex() if(!is.vector(bltr, mode = "numeric")) stop("need vector of From,To or of x_bl,y_bl,x_tr,y_tr") else if(length(bltr) == 2) { if(is.null(direction) | is.null(value)) stop("need 'direction' (1|2) and ordinate|abscissa 'value'") if(bltr[1] >= bltr[2]) stop("need From < To") # buid horizontal/vertical mesh at given ordinate(s)/abscissa(s) switch(direction, for(val in value) Z <- append(Z, seq(bltr[1], bltr[2], pass) + 1i*val) , for(val in value) Z <- append(Z, val + 1i*seq(bltr[1], bltr[2], pass)) ) return(Z) } else if(length(bltr) != 4) stop("only one allowed, Horizontal/Vertical/Rectangle mesh") if(bltr[1] >= bltr[3] | bltr[2] >= bltr[4]) stop("incorect specification of the rectangle vertices") # buid rectangular mesh for(val in seq(bltr[2], bltr[4], pass)) Z <- append(Z, seq(bltr[1], bltr[3], pass) + 1i*val) # horizontal! return(Z) }
Dăm un exemplu de testare a funcţiei (în care evidenţiem şi faptul că putem scurta numele unor parametri, condiţia fiind ca prefixele alese să nu coincidă unul cu altul):
> build_mesh(p=0.25, v=5, d=2, bltr=c(1, 3)) [1] 5+1.00i 5+1.25i 5+1.50i 5+1.75i 5+2.00i [6] 5+2.25i 5+2.50i 5+2.75i 5+3.00i > build_mesh(c(1, 3), p=0.5, v=seq(5, 6, 0.5), d=2) [1] 5.0+1.0i 5.0+1.5i 5.0+2.0i 5.0+2.5i 5.0+3.0i [6] 5.5+1.0i 5.5+1.5i 5.5+2.0i 5.5+2.5i 5.5+3.0i [11] 6.0+1.0i 6.0+1.5i 6.0+2.0i 6.0+2.5i 6.0+3.0i > plot(build_mesh(c(1, 1, 2, 2), p=0.05))
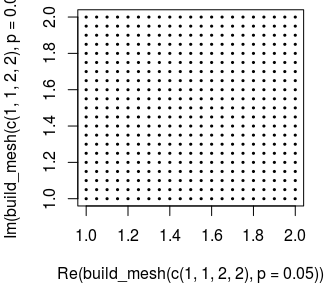
Doar în trecere precizăm că era posibilă o abordare generală, bazată pe scrierea ecuaţiei dreptei sub forma Z = (1 - t) A + t B, unde t este un parametru real, iar A şi B sunt două puncte date (ca numere complexe - "afixele" punctelor); pentru t ∈ [0, 1] am obţine segmentul [AB]. Ulterior, am putut constata că era mai bine să fi cerut în parametrul 'bltr' un vector complex (afixul colţului stânga-jos şi afixul colţului opus); adică ar fi fost mai bine să vizăm punctele în mod unitar, angajând mereu afixele lor - în loc de a folosi uneori vectori reali şi alteori vectori complecşi.
Să considerăm mai departe, pătratul de colţuri (-2, -2) şi (2, 2); îl împărţim în 64 de pătrăţele (sau "câmpuri", cum zicem în cazul tablei de şah), ducând paralele cu axele (cu pasul 4/8 = 0.5). Vrem să vizualizăm cum se transformă verticalele şi orizontalele rezultate, precum şi unele câmpuri alese într-un cadran sau altul.
Pentru a determina coordonatele colţurilor unui câmp (fiind necesare funcţiei build_mesh()) este suficient să ştim coordonatele centrului pătrăţelului respectiv; următoarea funcţie returnează un vector complex, constituit din afixele centrelor celor 64 de câmpuri:
build_centroid <- function() { Z <- as.complex() for(x in seq(-1.75, 1.75, 0.5)) # parcurge de la stânga spre dreapta for(y in seq(-1.75, 1.75, 0.5)) # parcurge câmpurile de jos în sus Z <- append(Z, x + 1i*y) return(Z) # afixele centrelor celor 64 de câmpuri }
În vectorul rezultat, cele 64 de câmpuri sunt indexate de la stânga spre dreapta şi de jos în sus - încât ne va fi uşor să indicăm unul sau altul dintre ele; pentru câmpurile ale căror centre le-am selectat din acest vector, vom avea nevoie eventual, de coordonatele colţurilor:
build_bltr <- function(cg) { # 'cg' este afixul "centrului de greutate" bl <- cg - (0.25 + 1i*0.25) tr <- cg + (0.25 + 1i*0.25) bltr <- c(Re(bl), Im(bl), Re(tr), Im(tr)) return(bltr) # coordonatele colţurilor stânga-jos şi dreapta-sus }
Să alegem acum câte un set de culori, pentru a evidenţia liniile (orizontale sau verticale) şi imaginile corespunzătoare acestora prin transformarea z−> z2, respectiv pentru a colora pătrăţelele pe care le vom selecta şi imaginile acestora:
require(RColorBrewer) # Creates nice looking color palettes col_line <- brewer.pal(8, "Dark2") # pentru linii col_rect <- brewer.pal(8, "Set2") # pentru dreptunghiuri
Construim acum reţelele de puncte corespunzătoare dreptelor orizontale şi respectiv verticale, care delimitează liniile şi respectiv, coloanele de câmpuri:
mesh_h <- build_mesh(c(-2, 2), p=0.01, v=seq(-2, 2, 0.5), d=1) mesh_v <- build_mesh(c(-2, 2), p=0.01, v=seq(-2, 2, 0.5), d=2) n <- length(mesh_h) / 9 # numărul de puncte de pe fiecare linie
Primele 'n' afixe din 'mesh_h' corespund dreptei orizontale y=-2, următoarele 'n' - dreptei y=-1.5, ş.a.m.d.; zona din mijloc corespunde punctelor axei orizontale. Vom colora la fel câte două drepte care sunt simetrice faţă de axa orizontală (de exemplu, y=-1.5 şi y=1.5), iar axa orizontală o vom colora cu negru. Gândim la fel şi pentru cazul dreptelor verticale - instituind următorii vectori de culori asociate respectiv punctelor din cei doi vectori determinaţi mai sus:
hcol <- c(rep(col_line[1:4], each = n), rep("black", each = n), # punctele axei reale rep(rev(col_line[1:4]), each = n)) vcol <- c(rep(col_line[5:8], each = n), rep("red", each = n), # punctele axei imaginare rep(rev(col_line[5:8]), each = n))
De exemplu, valorile din primul şi din ultimul grup de câte 'n' valori din 'hcol' sunt egale şi reprezintă culoarea punctelor dreptelor (simetrice faţă de axa orizontală) y=-2 şi y=2.
Trecem peste faptul că în acest moment (eventual, în scopul testării lucrurilor), am putea deja să plotăm punctele respective şi transformatele acestora. Să ne gândim întâi la constituirea reţelei de puncte corespunzătore unui set de câmpuri:
fields <- build_centroid() # afixele centrelor celor 64 de câmpuri fld1 <- fields[c(4, 5, 42, 43, 46, 47, 50, 55)] # de colorat şi transformat fld2 <- fields[c(37, 40, 28, 25, 36, 33, 29, 32)] # transformăm doar centrele Zcg <- sapply(fld1, function(cg) build_bltr(cg)) # coordonatele colţurilor (coloane) mesh_rect <- apply(Zcg, 2, function(d) build_mesh(d, pass=0.02)) Zcg <- t(Zcg) # linii de coordonate ale colţurilor opuse ale câmpurilor
Am ales în 'fld1' 8 câmpuri pe care le vom colora şi transforma punct cu punct şi în 'fld2' alte 8 câmpuri, pentru care vom determina doar transformatele centrelor (şi le vom eticheta).
sapply() ne-a permis să aplicăm pe fiecare câmp (reprezentat în 'fld1' prin afixul centrului) funcţia build_bltr() - rezultând matricea 'Zcg', în care fiecare coloană conţine coordonatele a două colţuri opuse ale câte unui câmp. Apoi, aplicând pe coloanele acestei matrice funcţia build_mesh() am obţinut reţeaua de puncte 'mesh_rect' care corespunde reuniunii celor 8 câmpuri.
În final, am transpus matricea 'Zcg': pe primele două coloane avem acum coordonatele colţurilor stânga-jos, iar pe următoarele două avem coordonatele colţurilor dreapta-sus - încât un apel rect() pentru cele patru coloane de coordonate va colora "deodată" cele 8 câmpuri.
Alegem să vizualizăm lucrurile în două panouri grafice alăturate (unul pentru punctele z, celălalt pentru punctele z2):
opar <- par(mfrow = c(1, 2), las=1, mar=c(2,2,0,0)) # două panouri alăturate
Setarea 'las=1' asigură că etichetele care marchează axa verticală vor avea orientarea obişnuită (şi nu vor fi scrise perpendicular pe axă); am folosit 'mar' pentru a reduce (jos şi stânga) sau a anula (sus şi dreapta) marginile obişnuite într-un panou grafic.
În primul panou plotăm reţeaua de puncte orizontale 'mesh_h' şi reţeaua 'mesh_v' de puncte verticale, iar apoi - folosim rect() pentru a colora pătrăţelele indicate prin colţuri în matricea 'Zcg' şi folosim text() pentru a eticheta pătrăţelele ale căror centre le avem în vectorul 'fld2':
plot(mesh_h, pch=21, cex=0.2, col=hcol) par(new = TRUE) # pentru a continua plotarea în acelaşi panou plot(mesh_v, pch=21, cex=0.2, col=vcol) rect(Zcg[, 1], Zcg[, 2], Zcg[, 3], Zcg[, 4], col=col_rect, border=NA) text(fld2, cex=1, col="sienna4")
În mod obişnuit, o comandă plot() iniţializează fereastra grafică ("ştergând" graficul existent), sau eventual, activează panoul următor dacă există; pentru a continua plotarea în acelaşi panou, peste graficul existent - trebuie intercalată prin funcţia par() setarea "new=TRUE", ca mai sus.
În al doilea panou plotăm pătratele reţelelor respective de puncte şi pătratul vectorului 'fld2' (adăugând şi etichetele aferente acestuia):
plot(mesh_h^2, pch=21, cex=0.2, col=hcol) par(new = TRUE) plot(mesh_v^2, pch=21, cex=0.2, col=vcol) for(i in 1:8) points(mesh_rect[, i]^2, pch=19, cex=0.1, col=col_rect[i]) fld2 <- fld2^2 + c(0.1+1i*0.1, 0.1, -0.1+1i*0.1, -0.1, 0.1-1i*0.2, 0.1, -0.1-1i*0.2, -0.1) points(fld2, pch=18, cex=1.25, col="sienna4") text(fld2, cex=0.9, col="sienna4", pos=c(2, 2, 4, 4)) grid() # adaugă linii de ghidare faţă de axe par(opar) # reconstituie parametrii grafici iniţiali
Pentru lizibilitate, am deplasat puţin punctele din 'fld2 ^ 2' - adăugând într-o direcţie sau alta 0.1 sau 0.2; bineînţeles că au fost necesare câteva încercări, inclusiv pentru a alege valorile de mai sus pentru 'pch' (forma punctelor), 'cex' (mărimea punctelor) şi 'pos' (poziţia etichetelor).
Bineînţeles că am înscris secvenţele de comenzi prezentate succesiv mai sus într-un fişier pe care în final, l-am executat din consola R folosind comanda source(); iată rezultatul (aproximativ - am mai ajustat pare-mi-se cu mouse-ul, trâgând de marginile ferestrei):
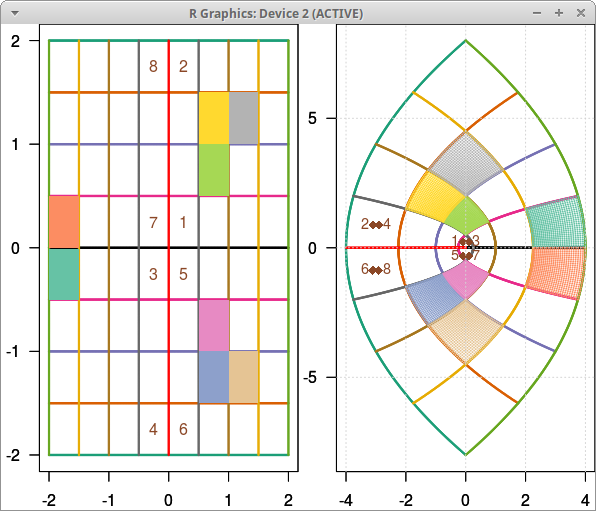
Văzând cum apar colorate "pătrăţelele" (şi imaginile acestora), n-avem decât să regretăm că în build_mesh() (şi apoi în build_bltr()) ne-a scăpat să vizăm doar interioarele dreptunghiurilor (nu şi punctele de pe laturi)… Precizăm că se poate urmări pas cu pas construcţia figurii - trasarea orizontalelor, a verticalelor, marcarea câmpurilor, apoi trasarea transformatelor orizontalelor, verticalelor şi câmpurilor - ambalând secvenţa de comenzi respectivă într-o funcţie şi folosind comanda debug() pentru aceasta (după source() pentru fişierul respectiv).
De pe figura obţinută, corelând culorile de linii din cele două panouri - deducem în primul rând că transformatele dreptelor respective au aparenţa unor parabole care au ca axă de simetrie axa reală: la câte două drepte verticale care sunt la fel colorate (adică sunt simetrice faţă de axa imaginară) corespunde o parabolă (la fel colorată) deschisă spre stânga; iar la câte două drepte orizontale care sunt la fel colorate (simetrice faţă de axa reală) corespunde o parabolă (la fel colorată) deschisă spre dreapta.
Axa reală (colorată cu negru) s-a transformat (în al doilea panou) în semiaxa reală pozitivă, iar axa imaginară (colorată cu roşu) - în semiaxa reală negativă (parabole "degenerate"); pentru acest caz este uşor de dat justificarea matematică: dacă x este număr real (punct al axei reale), atunci x2 ≥ 0 (deci se află pe semiaxa reală pozitivă); iar pentru punctele y i (cu y număr real oarecare) aflate pe axa imaginară, avem (y i)2 = -y2 (care se află pe semiaxa reală negativă).
Observând cum sunt transformate câmpurile etichetate cu 1 şi 3 (sau 7 şi 5, sau 2 şi 4) am putea înţelege că o pereche oarecare de câmpuri simetrice faţă de originea sistemului de axe este transformată într-o aceeaşi regiune - delimitată de câte două perechi de arce de parabolă (eventual, "degenerată") consecutive şi la fel deschise (spre stânga şi respectiv, spre dreapta).
2. Justificări matematice
Justificarea aspectelor vizualizate şi formulate mai sus decurge din proprietăţile definitorii ale numerelor complexe (incluzând şi operaţiile specifice) şi eventual, din maniera de implementare a acestora.
Orice punct din plan, P (x, y) - să excludem totuşi originea O(x=0, y=0) - este reprezentat în mod unic prin vectorul de poziţie OP şi deasemenea, prin numărul complex z = x + i y (unde prin definiţie, i2 = -1); dacă ρ este lungimea acestui vector, iar θ măsoară în radiani înclinarea lui faţă de semiaxa reală pozitivă, atunci proiecţiile pe axe ale lui P sunt x = ρ cos(θ) şi y = ρ sin(θ) - încât avem imediat şi reprezentarea z = ρ (cos(θ) + i sin(θ)), sau cu formula lui Euler, z = ρ ei θ.
Unghiul θ (numit "argument" al lui z, sau "fază") nu este unic determinat: adăugând sau scăzând (de oricâte ori) 2π obţinem acelaşi punct P - fiindcă sin() şi cos() sunt funcţii periodice, cu perioada principală 2π. Pentru a asigura unicitatea inversării (de la coordonate ρ, θ la coordonate x, y), trebuie ca θ să fie restricţionat la un anumit interval "principal" de lungime 2π - de regulă (-π, π], însemnând că pentru vectorii care "mătură" dinspre semiaxa reală pozitivă semiplanul de deasupra axei reale, θ creşte în sens antiorar de la 0 la π, iar pentru semiplanul opus acestuia θ descreşte în sens orar de la 0 spre -π.
"La limită", ajungem eventual într-un impas: ce argument are un punct situat pe semiaxa reală negativă (π, sau -π)? Argumentul principal este determinat prin atan2(y, x) şi putem constata simplu că în R problema este "rezolvată" ţinând cumva cont de semn (după cum s-ar ajunge la punct, din semiplanul superior sau din cel inferior):
> atan2(0, -1) # z = -1 + 0i (văzut ca fiind în semiplanul superior) [1] 3.141593 > atan2(-0, -1) # z = -1 - 0i (în semiplanul inferior) [1] -3.141593
Deducem că "+ 0i" vizează semiaxa imaginară din semiplanul superior, iar "- 0i" pe cea din semiplanul inferior (desigur… 0 nu este acelaşi lucru cu -0).
Avem z2 = ρ2e2θ i, ceea ce înseamnă că prin ridicare la pătrat argumentul se dubleză (şi este sarcina funcţiilor interne să-l reducă la valoarea principală).
Să considerăm o dreaptă paralelă axei imaginare,
z = a + i t (a ≠ 0, t ∈ R)
Ca exemplu, în figura de mai jos am schiţat două drepte verticale care sunt simetrice faţă de axa imaginară: una prin punctele "conjugate" z1 şi z2 (colorată cu negru în semiplanul superior şi cu albastru în semiplanul inferior) şi cealaltă prin punctele opuse acestora, -z1 şi respectiv -z2.
Pătratele punctelor z sunt:
z2 = a2 - t2 + 2at i
Deci când z parcurge verticala x=a (a ≠ 0), punctul z2 parcurge o curbă de gradul al doilea ale cărei "ecuaţii parametrice" sunt:
x = a2 - t2, y = 2at (t ∈ R)
Eliminând parametrul, cum se obişnuieşte - obţinem:
x = - y2 / (4a2) + a2
şi recunoaştem ecuaţia unei parabole care are ca axă de simetrie axa reală, are vârful în punctul (a2, 0) şi este deschisă spre stânga - având focarul în originea sistemului de axe, iar ca directoare, dreapta x = 2a2. În figura de mai jos, această parabolă - corespunzătoare dreptelor simetrice faţă de axa imaginară duse prin punctele z1 şi respectiv (-z1) - este conturată cu negru în semiplanul superior şi cu albastru în semiplanul inferior.
Pentru cazul unei drepte orizontale, am putea relua calculul de mai sus - dar nu este necesar: dreapta y = a (orizontală) se poate obţine prin rotirea cu 90° a dreptei verticale x = a; dacă z este un punct al dreptei x = a, atunci i*z aparţine dreptei y = a (fiindcă argumentul lui i este π/2, iar prin înmulţire "argumentele se adună"); rezultă că (i*z)2 (care face -z2) reprezintă transformatele punctelor dreptei orizontale - adică, ecuaţia parabolei corespunzătoare dreptei y = a se obţine schimbând semnele în ultima ecuaţie de mai sus:
x = y2 / (4a2) - a2
ceea ce reprezintă o parabolă simetrică faţă de axa imaginară, celeia prezentate anterior.
În figura de mai jos am schiţat cu roşu şi verde, dreptele orizontale prin punctele conjugate z3 şi z4, precum şi parabola (deschisă spre dreapta) corespunzătoare acestora:
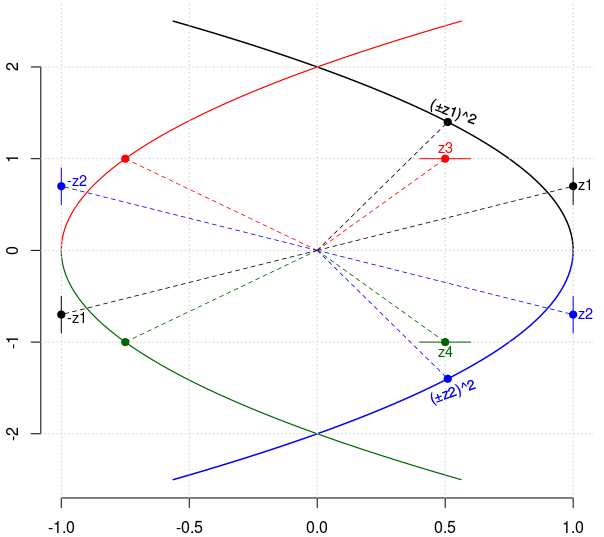
Se vede că axele nu sunt măsurate cu o aceeaşi unitate - încât nu este evident pe figură, că argumentul punctului (±z1)2 este dublul argumentului lui z1 (şi la fel, argumentul punctului roşu de pe parabolă corespunzător lui z3 este dublul argumentului acestuia, etc.).
Am evidenţiat pe figură că punctele (simetrice faţă de origine) z1 şi (-z1) sunt transformate într-un acelaşi punct (±z1)2 (şi la fel pentru punctele marcate cu albastru, etc.); formulând mai general - semidreptele cu originea pe axa reală (şi la fel, cele cu originea pe axa imaginară) care sunt simetrice faţă de originea sistemului de axe sunt transformate într-o aceeaşi semiparabolă, situată fie în semiplanul superior, fie în cel inferior.
Nu mai reproducem aici, programul prin care am trasat figuri precum cea redată mai sus (bazat desigur, pe funcţiile plot(), lines(), points(), segments() şi text(), angajând un vector complex dat).
3. Pătratul tablei de şah
Considerăm din nou, pătratul de colţuri (-2, -2) şi (2, 2) care fusese împărţit (în mod implicit) în cadrul funcţiei build_centroid() în 64 de pătrăţele (indexate de jos în sus şi de la stânga spre dreapta). Pentru a vizualiza transformarea prin "ridicare la pătrat" a tablei de şah este suficient să o aplicăm primelor 32 de câmpuri (având în vedere simetriile evidenţiate mai sus; transformatele câmpurilor 33..64 se vor suprapune transformatelor câmpurilor 1..32).
Cele două culori ale câmpurilor tablei de şah alternează în funcţie de paritatea sumei indicilor de linie şi de coloană - încât instituim întâi o funcţie care să returneze culoarea corespunzătoare câmpului indicat:
set_col <- function(n, white="gray50", black="sienna4", alpha=25) { q <- (n-1) %/% 8 + 1 # coloana 1..8 r <- (n-1) %% 8 + 1 # linia 1..8 return(ifelse((q + r) %% 2, rgb(t(col2rgb(white)), alpha=alpha, max=255), rgb(t(col2rgb(black)), alpha=alpha, max=255))) }
Am folosit rgb() pentru a seta cele două culori, fiindcă astfel putem adăuga culorii (indicate în primii trei parametri, obţinuţi prin transpunerea matricei returnate de col2rgb()) un anumit nivel de transparenţă - pentru situaţia în care transformatele câmpurilor s-ar suprapune (în întregime cum am întâlnit deja anterior, sau parţial - ca în cazul când am considera de exemplu, cuburile punctelor în loc de pătratele acestora).
Determinăm reţeaua punctelor (cu un "pas" ca 0.005) corespunzătoare primelor 32 de câmpuri (sau tuturor câmpurilor, sau numai primelor 16, etc.) - folosind funcţiile din §1 build_centroid(), build_bltr() şi build_mesh() - şi o "ridicăm la pătrat" (sau la cub, de exemplu); în final, plotăm pe rând reţeua rezultată pentru fiecare dintre aceste câmpuri:
fields <- build_centroid() # afixele centrelor celor 64 de câmpuri convert <- function(id_fld=1:32, to=2, pass=0.005, file=NULL, ...) { Zcg <- sapply(fields[id_fld], function(cg) build_bltr(cg)) mesh <- apply(Zcg, 2, function(d) build_mesh(d, pass=pass)) mesh <- mesh ^ to # puterea 'to' a afixelor punctelor de pe câmpurile 'id_fld' if(!is.null(file)) png = png(filename = paste(file, ".png", sep=""), bg="transparent") opar <- par(mar=c(0, 0, 0, 0), bty="n", xaxt="n", yaxt="n") plot(mesh, type="n") # , asp=0.9) for(i in 1:length(id_fld)) # plotează transformatele câmpurilor points(mesh[, i], pch=19, cex=0.2, col = set_col(i, ...)) par(opar) if(!is.null(file)) dev.off() }
Argumentul "..." din funcţia de mai sus serveşte pentru a transmite parametri funcţiei set_col(i, ...) (apelate prin points() dinăuntrul funcţiei convert(), pentru a seta culoarea cu care vor fi plotate punctele reţelei corespunzătoare câmpului de rang "i").
Următoarele trei imagini corespund respectiv apelurilor:
convert(alpha=255, f="boardTo2") convert(id=1:64, to=1, f="boardTo1") convert(id=1:16, to=3, p=0.001, alpha=4, f="boardTo3")



reprezentând pătratul reţelei de puncte asociate tablei de şah şi apoi chiar reţeaua punctelor tablei; iar a treia imagine (de mai sus) reprezintă cubul reţelei de puncte asociate primelor 16 câmpuri ale tablei de şah (parcurgând de la stânga spre dreapta şi de jos în sus).
Imaginile care s-ar obţine pentru "to = 3", angajând alte câmpuri decât cele 16 considerate în ultimul apel de mai sus devin prea "încărcate" pentru a fi luate în seamă; dar pentru încă vreo câţiva exponenţi (4, 5, 11 de exemplu) şi pentru anumite alegeri de câmpuri (primele 8, respectiv câmpurile din colţuri) - încă obţinem imagini interesante:
convert(id=1:8, to=4, p=0.0015, f="boardTo4") # prima imagine de mai jos convert(id=1:8, to=5, p=0.0015, alpha=10, white="black", black="darkgreen", f="boardTo5") convert(to=11, id=c(1,8,57,64), p=0.001, alpha=6, white="navyblue", black="navy", f="boardTo11")



Pentru setul câmpurilor din colţurile tablei încă apar imagini interesante pentru exponenţii 4 (când cele patru câmpuri - fiind opuse două câte două şi pe o diagonală şi pe cealaltă - au o aceeaşi transformată), sau 5, 6, 7 sau 9.
Este de remarcat că avem simetrie faţă de axa reală, dar nu şi faţă de axa imaginară (exceptând cazul ridicării la pătrat şi cazul unor selecţii particulare de câmpuri; dar o justificare simplă a acestui fapt… mai are de aşteptat.
4. Alte transformări ale tablei de şah (anticipări)
Oarecum întâmplător, am observat că pentru exponenţi "to" ca 0.5, 1/3, 0.25, 0.75, sau 5/6 (poate că pentru orice exponent raţional, dar nu prea pot justifica) - obţinem cam aceeaşi imagine ca în cazul implicit "to = 2" (prima dintre ultimele 6 imagini de mai sus).
În orice caz, apare ideea de a aplica reţelei de puncte a tablei de şah diverse alte transformări, înlocuind linia "mesh <- mesh ^to" din cadrul funcţiei convert() cu "mesh <- cos(mesh) ^to", sau cu "mesh <- exp(mesh) ^to" (de exemplu):
convert(to=1, p=0.002, f="boardcos") # mesh <- cos(mesh) ^ to convert(to=0.5, p=0.002, f="boardcos0.5") convert(to=1/3, p=0.002, f="boardcos0.3") convert(to=0.5, p=0.002, f="boardexp") # mesh <- exp(mesh) ^ to


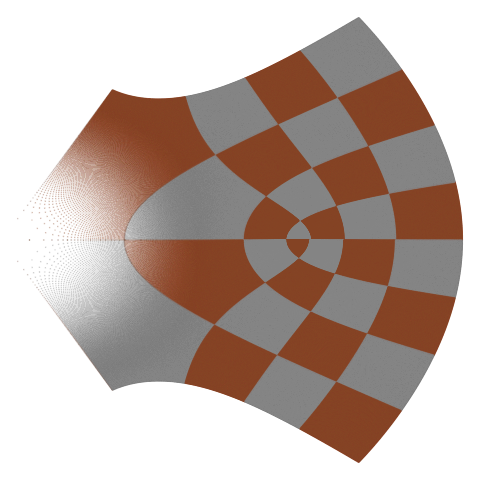

Prima imagine este rezultatul aplicării funcţiei (de variabilă complexă) cos(); pentru a doua şi a treia - s-a aplicat cos() şi radicalul de ordin 2, respectiv de ordin 3; a patra imagine - care dintre toate, seamănă cel mai bine cu o tablă de şah (în perspectivă, după ce a fost "îndoită" în jurul axei centrale) - s-a obţinut prin exp(), urmat de radical de ordinul doi.
Vom justifica într-o a doua parte, analog secţiunii §2 de mai sus, că prin cos() dreptele orizontale se transformă în elipse, iar dreptele verticale - în hiperbole; se recunosc aceste curbe, pe prima imagine (fiind "deformate" pe următoarele două imagini, fiindcă pentru acestea s-au aplicat şi radicali). Dar de ce elipsele vizibile în prima imagine sunt "trunchiate" în partea lor stângă?
La fel, vom vedea că funcţia exp() transformă dreptele verticale în cercuri şi dreptele orizontale în anumite raze emanate din origine; dar de ce aceste cercuri (pe care par dispuse câmpurile tablei în ultima imagine) sunt… "trunchiate"?
Se poate constata că înlocuind "cos(mesh)" prin "cos((pi/2)*mesh)" şi respectiv, "exp(mesh)" prin "exp((pi/2)*mesh)" - obţinem elipse şi respectiv cercuri complete (în prima şi respectiv a patra imagine de mai sus); se vede că n-am fost inspirat, alegând din capul locului intervalul [-2, 2] ca bază pentru construcţia tablei de şah… Anticipând, ideea de a considera factorul multiplicativ π/2 vine de la faptul că funcţiile complexe cos() şi exp() sunt periodice şi de regulă, implementările consideră ca "principal" intervalul (-π π] - ori aici ne bazasem doar pe [-2, 2], ceea ce a condus la "trunchierea" evidenţiată mai sus, cum vom arăta ceva mai încolo.
vezi Cărţile mele (de programare)