Reprezentarea funcţiilor (javaScript, MathML, canvas)
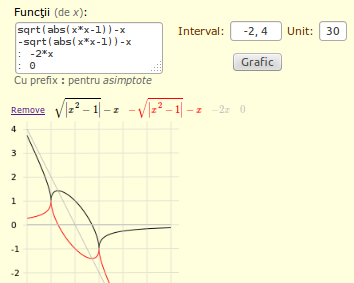
Evocăm alături o aplicaţie de reprezentare grafică a funcţiilor, montată deja la Grafice (şi dezvoltată plecând de la [1])
Se introduc funcţii (eventual, corelate între ele), se indică un interval de definiţie comună şi o măsură a unităţii (pixeli); butonul "Grafic" va adăuga o linie pe care sunt scrise funcţiile şi un <canvas> cu graficele corespunzătoare.
Funcţiile se introduc folosind sintaxa obişnuită din C sau javaScript (cu operaţiile +, -, *, / şi cu funcţiile predefinite "sqrt", "abs", etc.), dar vor fi afişate în notaţia matematică obişnuită.
În cazul redat, "corelarea" funcţiilor constă în faptul că împreună, ele reprezintă o hiperbolă de asimptote `y = 0` şi `y = -2x` şi o elipsă tangentă (la abscisele -1 şi 1) ramurilor acesteia.
"Funcţie", dar cu trei sensuri
Pentru un script javaScript - "funcţie" înseamnă un obiect javaScript instanţiat direct din obiectul predefinit Function() (var myFunc = new Function();), sau rezultat prin interpretarea unei definiţii de forma: function myFunc(lista_de_parametri) { "corpul" funcţiei }; această definiţie poate fi "relaxată" în anumite condiţii, prin omiterea numelui 'myFunc' - creând astfel funcţii anonime.
Ca şi oricare obiecte, funcţiile pot fi "grupate" în pachete; astfel, obiectul javaScript predefinit Math() grupează funcţiile matematice standard - permiţând folosirea directă în programe: Math.sqrt(3) invocă funcţia "radical de ordinul doi", furnizând valoarea lui `sqrt(3)`.
Pe de altă parte, pentru utilizator - "funcţie" poate însemna ceea ce i se cere să tasteze într-o casetă <textarea> (precum "Funcţii", în imaginea de mai sus). Mizăm fireşte pe un "utilizator decent" - care ştie să folosească "sqrt()" (nu neapărat şi Math.sqrt()) pentru a introduce "radical" şi ştie deasemenea că "sqrt(x)" şi "pow(x, y)" sunt definite numai pentru valori x pozitive.
Vizând şi un anumit interes matematic, excludem utilizatorul "mură'n gură" (redus la Microsoft-Word şi la point-and-click) - acestuia ar fi trebuit să-i punem la dispoziţie nu un <textarea> în care să tasteze (direct) funcţia, ci icon-uri frumoase cu care să "construiască" (lăturalnic) funcţiile de introdus (click pe icon-ul `bbsqrt\ ` pentru a introduce "radical", click pe + pentru "plus", ş.a.m.d.).
În sfârşit, ar fi vorba de "funcţie" în sensul notaţiei matematice obişnuite; adică exprimată nu prin "pow(3*x*x - 4*x + 5, 1/3)" (cum s-ar introduce în caseta "Funcţii"), ci prin `root{3}{3x^2 - 4x + 5}`.
Forma textuală (simplificată) tastată de utilizator în <textarea> trebuie "transformată" pe de o parte, în obiect intern Function() (pentru a putea calcula valorile funcţiei în punctele intervalului), iar pe de altă parte - în "notaţie matematică" obişnuită (pentru afişarea finală).
Introducerea funcţiilor şi evaluarea acestora
Oferim utilizatorului două simplificări, faţă de cerinţele introducerii funcţiilor în javaScript. Mai întâi, îl scutim de "prefixul" Math. pentru funcţiile standard; astfel, cerem "simplu" sqrt(abs(x*x-1)) în loc de formula "corectă" Math.sqrt(Math.abs(x*x-1)). Altfel spus - dacă în textul tastat de către utilizator programul întâlneşte un nume "id" care este definit în Math() - ceea ce se poate testa folosind Math.hasOwnProperty("id") - atunci programul îl va înlocui cu "Math."+"id" (liniile 15-18).
Apoi, îl scutim de ambalarea definiţiei sale în function(x) { return (definiţia respectivă); }: dacă myDef este definiţia "simplificată" tastată de către utilizator şi apoi rezolvată în privinţa prefixului Math., atunci folosim eval("f=function(x){return (" + myDef + ")}") pentru "ambalarea" (linia 19) care este necesară pentru obţinerea ulterioară a unui obiect Function():
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | var Utils = { /* ... pachet de funcţii utilitare (vezi [1]) ... */ get_function: function(id_txt) { var fx = document.getElementById(id_txt).value .replace(/^\s+|\s+$/g, "").split('\n'), func = [], nume = /(?:[a-zA-Z][a-zA-Z0-9_]*)/g; for(var i=0, n=fx.length; i < n; i++) { var _fmc = {'func':'', 'asmath': '', 'color': ''}, f = fx[i].replace(/^\s+|\s+$/g, ""), asimp = false; if(/^\:\s*/.test(f)) { // : la început declară o asimptotă asimp = true; // asimptotele vor fi colorate "palid" f = fx[i] = f.replace(/^\:\s*/, ''); } f = f.replace(nume, function (id) { return Math.hasOwnProperty(id)? "Math." + id : (Umath.hasOwnProperty(id)? "Umath." + id : id); }); try { eval("f=function(x){return (" + f + ")}"); } catch(ex) { alert("Eroare: " + ex); return; } // alert(f); // function(x){return (Umath.root(3, x*x*x - 3*x + 1))} _fmc['func'] = f; _fmc['color'] = asimp ? 'silver' : this.colors()[i]; _fmc['asmath'] = this.toLatex(fx[i]); func.push(_fmc); } return func; } }; |
Utils.get_function() primeşte ca parametru identificatorul HTML al elementului <textarea> în care utilizatorul îşi introduce funcţiile; în linia 3 se preia textul conţinut, se elimină spaţiile de la început şi de la sfârşit şi se separă rândurile - rezultând tabloul fx[] ale cărui componente reprezintă fiecare câte una dintre definiţiile "simplificate" ale funcţiilor introduse.
Tabloul func[] introdus în linia 5 şi returnat în final (linia 27) este un tablou "paralel" cu fx[], fiind completat prin parcurgerea acestuia din urmă (în ciclul 7-26); anume, fiecărei definiţii din fx[] i se asociază (în liniile 22-25) un "dicţionar" conţinând exprimarea javaScript "corectă" a acelei definiţii de funcţie, culoarea prevăzută pentru graficul ei şi respectiv, expresia ASCIIMathML aferentă.
Linia 17 presupune existenţa unui obiect Umath{} care defineşte eventual diverse funcţii matematice suplimentare - de exemplu, "radicalul de ordin impar":
var Umath = { root: function(n, t) { return t>=0 ? Math.pow(t, 1/n) : -Math.pow(-t, 1/n); } /*, alte funcţii */ };
Funcţia Umath.root(n, x) permite şi valori x negative (ceea ce are sens pentru n impar) - spre deosebire de funcţia standard "echivalentă" pow(x, 1/n) (în care obligatoriu, x > 0).
De fapt (pentru un exemplu tipic de "ramificare"), funcţiile care sunt definite numai pentru `x > 0` pot fi "extinse" şi direct, folosind operatorul condiţional; de exemplu, se poate tasta
(x < -1 || x > 1)? pow(x*x-1, 1/3) : -pow(1-x*x, 1/3)
pentru a atribui valoarea `(x^2 - 1)^(1//3)` dacă `|x| > 1` respectiv `-(1 - x^2)^(1//3)` dacă `|x| ≤ 1` - cu precizarea că în acest caz, acelaşi lucru se obţine acum tastând root(3, x*x-1) (prefixul necesar "Umath." fiind adăugat în linia 17).
Utilizatorul va putea tasta drept "funcţie" şi alert('ceva'), sau chiar instrucţiuni mai periculoase; dar astfel… nu va putea "strica" decât propria sesiune de lucru, sau poate propriul browser.
Funcţiile anonime (vezi un exemplu în linia 21) înscrise astfel pe câmpurile 'func' ale "dicţionarelor" din tabloul returnat func[] vor fi apelate ulterior prin func[i]['func'](x), pentru a obţine valorile acelei funcţii în punctele intervalului de definiţie (pentru i = 0..func.length-1).
Notaţia matematică
Pentru un acelaşi concept matematic întâlnim notaţii diverse - depinzând de epocă, de contextul matematic, de convenţii naţionale (sau de limbajul de programare). În principiu, avem de distins între notaţia matematică (desemnând concepte matematice) şi "gândirea matematică" (prin care "se face" matematică, "evaluând" conceptele respective) - cam la fel cum am distins mai sus între exprimarea textuală a funcţiei şi respectiv, evaluarea acesteia ca obiect calculabil.
Pentru descrierea notaţiei matematice (dar nu pentru "a face" matematică) există două limbaje sau specificaţii de bază: TeX (sau, cu notaţia specifică: TeX) şi MathML - introduse cu 10 ani înainte şi respectiv, la 10 ani după apariţia Web-ului.
Dăm un exemplu de cum s-ar scrie un fişier HTML5 pentru a prezenta în browser o expresie matematică, angajând specificaţia MathML:
Firefox: 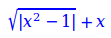
Opera: 
<!DOCTYPE html> <!-- HTML5 --> <head> <meta charset="utf-8"> <title>Test MathML (FireFox)</title> </head> <body> <math> <mstyle mathcolor="blue"> <!-- culoarea textului conţinut --> <msqrt> <!-- tag-ul pentru "rădăcină pătrată" --> <mrow> <!-- ambalează conţinutul pe o singură linie --> <mo>|</mo> <!-- <mo> pentru "operator" --> <msup> <!-- tag-ul pentru "superscript" --> <mi>x</mi> <!-- <mi> pentru "identificator" --> <mn>2</mn> <!-- <mn> pentru "număr" --> </msup> <mo>-</mo> <mn>1</mn> <mo>|</mo> </mrow> </msqrt> <mo>+</mo> <mi>x</mi> </mstyle> </math> </body>
Expresia respectivă este descrisă element cu element folosind anumite tag-uri şi ambalând întreaga descriere drept conţinut al unui tag <math>.
Fiecare simbol este etichetat corespunzător rolului său ('x' este un "identificator", având tag-ul <mi>; '+' este un "operator", cu tag-ul <mo>; etc.) şi se folosesc tag-uri speciale pentru a prezenta diverse funcţii matematice standard, sau diverse construcţii - <msqrt> va prezenta un radical de ordin 2, <mrow> prezintă conţinutul pe o aceeaşi linie, <mfrac> permite prezentarea de fracţii, etc.
Nu prea este convenabil de scris manual asemenea descrieri (element cu element, după "rol"); de aceea, s-au creat programe sau scripturi care produc automat codul MathML corespunzător unei expresii formulate "direct" - cel mai frecvent folosite fiind convertoarele între TeX şi MathML.
De exemplu, ASCIIMathML preia o asemenea scriere: `sqrt(|x^2 - 1|) + x` şi produce pentru ea aproximativ codul MathML din fişierul redat mai sus - ba mai mult, inserează secvenţa de cod rezultată în documentul HTML respectiv, încât la deschiderea fişierului în browser va apărea "direct" notaţia dorită: `sqrt(|x^2 - 1|) + x`.
 Iar folosind MatJax (configurat pe ASCIIMathML), codul MathML rezultat poate fi vizualizat şi prin meniul deschis prin click-dreapta pe expresie.
Iar folosind MatJax (configurat pe ASCIIMathML), codul MathML rezultat poate fi vizualizat şi prin meniul deschis prin click-dreapta pe expresie.
Revenind la aplicaţia noastră - noi am asumat că utilizatorul introduce expresia matematică folosind "notaţia" obişnuită în C/javaScript (asigurându-i unele simplificări şi - prin "modulul" Umath{} - unele posibilităţi de extensie); pentru expresia "simplificată" introdusă - am constituit codul javaScript necesar instanţierii ulterioare a unei Function() (pentru calcularea valorilor) şi am rezervat - vezi linia 24 din get_function() - un câmp pe care să constituim notaţia necesară lui ASCIIMathML pentru a construi codul MathML de redare în browser a expresiei respective.
Notă. Alternativa ar fi aceea de a cere utilizatorului direct notaţia ASCIIMathML pentru expresia respectivă şi să folosim apoi parserul şi evaluatorul din ASCIIMathMl; dar astfel… n-am mai fi avut plăcerea de a face o aplicaţie "proprie". Şi de fapt - interesul pentru MathML (sintetizat mai sus) este ulterior încropirii aplicaţiei de faţă, fiind dictat de necesitatea apărută în final de a "arăta" în browser notaţia matematică obişnuită a funcţiei.
Trecerea la notaţia ASCIIMathML
În linia 24 din Utils.get_function() se apelează metoda Utils.toLatex(); aceasta urmează să producă notaţia ASCIIMathML corespunzătoare expresiei "simplificate" primite.
Mai întâi, trebuie înlocuite unele denumiri de funcţii standard:
var Utils = { /* ... */ toLatex: function(fx) { if(/asin/.test(fx)) fx = fx.replace(/asin/g, 'arcsin'); // analog pentru 'acos', 'atan' /* ... */ return '`' + fx + '`'; } };
În C/javaScript avem "asin", "acos", "atan", "PI" dar în Latex (şi implicit, în ASCIIMathML) avem "arcsin", "arccos", "arctan", "pi" (pentru `pi`). În final (după toate transformările necesare), şirul "fx" trebuie ambalat între delimitatorii "`" (caracterul "accent grav") - ASCIIMathML va interpreta numai şirurile astfel delimitate (cu alternativa de delimitare specifică Latex-ului: "\$").
Un caz special avem pentru "abs": abs(expr) trebuie înlocuit cu |expr|:
if(/abs/.test(fx)) fx = fx.replace(/abs\(([^\)]*)\)/g, '|$1|');
Pentru fiecare - datorită folosirii modificatorului "global" /.../g - apariţie "abs(expr)" se captează "expr" în variabila specială "$1", se înlocuieşte "abs(" cu "|", se înscrie captura şi se înlocuieşte ")" cu "|".
Apoi, avem de-a face cu notaţia operaţiei de înmulţire. Pentru secvenţe C/javascript de forma "număr*..." (de exemplu, "2*x", sau "2*sin(x)", sau "2*x*x*x") - eliminăm caracterul "*":
fx = fx.replace(/(\d+\.?\d*)\*/g, '$1');
"Număr" înseamnă fie un şir nevid de cifre (descris de "\d+"), fie un asemenea şir urmat de "." şi eventual de încă un şir de cifre (ca în "1.25*x").
În schimb, pentru cazul expresiilor ca "x*x*x" (de înlocuit cu "x^3") nu am găsit o soluţie generică acceptabilă (în privinţa simplităţii) şi ne-am limitat la aşa ceva:
if(/x\*x/.test(fx)) { fx = fx.replace(/x\*x\*x\*x/g, 'x^4') .replace(/x\*x\*x/g, 'x^3') .replace(/x\*x/g, 'x^2'); }
Apoi, subexpresii ca "pow(expr, exponent)" trebuie transformate în "(expr)^(exponent)":
if(/pow/.test(fx)) { fx = fx.replace(/pow\(([^,]*),/g, '($1)^('); }
Se caută "pow(", se capturează în '$1' ceea ce urmează până la "," şi se înlocuieşte cu "($1)^(".
Funcţia Umath.root(n, expr) pe care am introdus-o mai la început are în ASCIIMathML exprimarea "root{n}{expr}" şi putem face conversia necesară prin:
if(/root/.test(fx)) { fx = fx.replace(/root\(([^,]*)\s*,\s*([^\)]*)\)/g, 'root{$1}{$2}'); }
Cele de mai sus - bazate toate pe metoda String.replace() şi pe lucrul obişnuit cu expresii regulate - acoperă suficient necesităţile de conversie care pot apărea în cazul nostru, chiar dacă există diverse "imperfecţiuni" (de exemplu, "pow(2, x)" va fi transformat în "(2)^x", în loc de "2^x"). Este clar însă că rezolvarea completă (să ne amintim de cazul "x*x*x*...*x") şi unitară a problemelor de conversie care pot să apară ar impune elaborarea prealabilă a unui parser adecvat.
Montarea notaţiei matematice în document
Reprezentarea astfel returnată de Utils.toLatex() este reţinută în câmpul func[i]["asmath"] (linia 24 din Utils.get_function()) şi va trebui inserată în documentul HTML în care utilizatorul a introdus funcţiile respective. Prin următoarea metodă - tot din Utils{} - creem un paragraf HTML conţinând un link "Remove" şi una după alta, valorile din câmpurile "asmath" ale obiectelor înregistrate în tabloul referit de parametrul primit:
var Utils = { /* ... */ to_html: function(func) { var info = ['<p style="font-size:11px;margin-bottom:0.5em;">'], h = []; info.push('<a href="" class="canvas-rem">Remove</a> '); for(var i=0, n=func.length; i < n; i++) h.push('<span style="color:'+ func[i]["color"] + '">', func[i]['asmath'],'</span>'); info.push(h.join(' ')); info.push('</p>'); return info.join(''); } }
Urmărim ca utilizatorul să poată adăuga un nou grafic la cele deja create şi să poată elimina din document un grafic anterior - de aceea am prevăzut link-ul "Remove". Dar am evitat să montăm imediat pe linkul creat, handler-ul "on-click" necesar pentru a declanşa eliminarea dorită - fiind preferabil să prevedem un singur handler pentru toate aceste link-uri (în loc de câte unul pentru fiecare), montat pe acea diviziune HTML care va conţine toate graficele adăugate (şi implicit, toate link-urile "Remove" ce vor fi create):
$('#hist-canvas').delegate("a", "click", function() { var tgt = $(this).parent(); // paragraful care conţine link-ul care a receptat click tgt.next().remove(); // elimină <canvas>-ul (graficul) aflat dedesubtul paragrafului tgt.remove(); // elimină şi paragraful respectiv return false; });
Am folosit aici metoda .delegate() a obiectelor jQuery() - definind un singur "handler", asociat diviziunii "hist-canvas" (unde se vor adăuga graficele create), prin care acţiunile prevăzute (aici, remove()) vor fi executate asupra acelui link interior care a receptat un click (ca şi cum acesta ar avea montat în modul obişnuit, un handler de click): se identifică paragraful care conţine link-ul care a receptat click-ul ("părintele" acelui link), se elimină din document elementul aflat dedesubtul acestui paragraf (în speţă, elementul <canvas> care conţine graficele funcţiilor notate în acel paragraf) şi în final se elimină însuşi paragraful respectiv.
Am arătat mai sus cum "eliminăm" - să vedem acum şi cum "adăugăm" în document ceea ce returnează Utils.to_html(). Dacă "add-grafic" este identificatorul butonului "Grafic" care va declanşa adăugarea dorită şi "funcţii" identifică elementul <textarea> în care s-au introdus funcţiile - atunci putem prevedea pe "Grafic" acest handler pentru click:
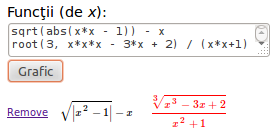
1 2 3 4 5 6 7 | $('#add-grafic').click(function(){ var func = Utils.get_function('functii'); // console.log(func); $('#hist-canvas').append(Utils.to_html(func)); MathJax.Hub.Queue(["Typeset", MathJax.Hub]); return false; }); |
În linia 1 se apelează Utils.get_function(), obţinând tabloul "func" al cărui conţinut se poate "vedea" (de exemplu, în browserul Chrome - prin meniul Tools/JavaScript Console) activând linia 3; pentru funcţiile din figură, cele două obiecte conţinute de acest tablou apar astfel:
[Object, Object] tabloul func[] conţine două obiecte 0: Object func[0] primul obiect asmath: "`sqrt(|x^2 - 1|) - x`" color: "black" func: function (x){return (Math.sqrt(Math.abs(x*x - 1)) - x)} 1: Object func[1] al doilea obiect asmath: "`root{3}{x^3 - 3x + 2} / (x^2+1)`" color: "red" func: function (x){return (Umath.root(3, x*x*x - 3*x + 2) / (x*x+1))}
În linia 4 se apelează Utils.to_html(), conducând la adăugarea în diviziunea "hist-canvas" a unui paragraf care conţine link-ul "Remove" şi pe câte un <span>, câmpurile "asmath" ale obiectelor din tabloul "func":
<div id="hist-canvas"> <p style="font-size:11px;margin-bottom:0.5em;"> <a href="" class="canvas-rem">Remove</a> <span style="color:black">`sqrt(|x^2 - 1|) - x`</span> <span style="color:red">`root{3}{x^3 - 3x + 2} / (x^2+1)`</span> </p> </div>
Apoi, în linia 5 se foloseşte funcţionalitatea bibliotecii MathJax; desigur, aceasta trebuie "inclusă" în prealabil - printr-un element <script src=".../MathJax.js ?config = AM_HTMLorMML-full"> adăugat în <head>-ul documentului. MathJax este activat automat imediat după ce browserul a încărcat documentul, având următoarea funcţionalitate de bază: caută toate apariţiile de şiruri delimitate (în cazul nostru) de '`' (caracterul "accent grav") şi le înlocuieşte cu secvenţa corespunzătoare de cod MathML (producând în browser "notaţia matematică" aferentă).
Doar că în cazul nostru, şirurile respective sunt rezultatul introducerii funcţiilor de către utilizator, în momente ulterioare încărcării documentului - deci ulterior etapei în care MathJax a activat automat; prin urmare, prin linia 4 (vezi Modifying Math on the Page) am "reactivat" MathJax (care acum, va "vedea" numai noile şiruri încadrate de '`' - cele vechi au fost deja înlocuite prin cod MathML). Rezultatul înlocuirii de către MathJax a şirurilor respective se poate vedea folosind de exemplu meniul View Source/View Generated Source (în Firefox).
Reprezentarea grafică a funcţiilor
Producerea graficelor funcţiilor este partea esenţială a aplicaţiei; dar această parte a fost prezentată deja în [1] - faţă de care Grafice face doar câteva modificări uşor de anticipat.
Baza de plecare a acestor modificări a fost renunţarea la trasarea graficelor "prin puncte" - în [1] folosisem metoda fillRect(), reprezentând punctele consecutive ale graficului prin mici pătrăţele (0.75px), distanţate între ele în funcţie de pasul ales de către utilizator prin parametrul "step" al constructorului Grafic(). Trasând acum "prin linii" (cu metoda lineTo(), de la punctul curent la cel următor), putem renunţa la parametrul "step" - fiind suficientă valoarea fixată 0.01 (valorile funcţiei vor fi calculate din sutime în sutime).
În [1] ne-am cramponat de ideea de a pune la punct un procedeu de calculare a unui "factor de scalare" FS (acelaşi pe ambele axe) în corelaţie cu mărimea valorilor funcţiilor şi a intervalului de definiţie. Acum considerăm FS în cel mai firesc mod: este numărul de pixeli ales de către utilizator pentru unitatea de măsură (înlocuind parametrul "step" din constructorul Grafic()).
O corectare simplă - dar importantă - vizează utilizarea metodei Utils.scale(): în [1] foloseam pentru punctul curent din tabloul valorilor funcţiilor, Utils.scale(y[i], ymin, ymax, 0, H) şi analog pentru abscise - adică, se accesa obiectul Utils{}, din care se accesa şi apoi se apela metoda scale() a acestuia, pentru fiecare punct (de 100 de ori, pentru fiecare funcţie - dacă step=0.01); acum am "scos în afara" ciclurilor accesul la Utils.scale(), definind în afara ciclului care parcurge tabloul valorilor funcţiilor referinţa var scale = Utils.scale; - încât acum, în interiorul ciclului se face doar apelarea funcţiei referite de scale (nu şi atâtea operaţii de accesare).
În sfârşit - am modificat marcarea coordonatelor: dacă factorul de scalare indicat de utilizator este cel puţin 60 de pixeli şi dacă lungimea intervalului de definiţie, sau diferenţa dintre cea mai mare şi cea mai mică valoare a funcţiilor introduse este mai mică decât 4, atunci marcăm coordonatele (şi trasăm "gridul") cu pasul 0.5 (altfel, din unitate în unitate); desigur, puteam folosi pasul 0.25 de exemplu - dar 0.5 (ca şi celelalte valori fixe menţionate) ni se pare rezonabil.
Desigur, ne punem problema de a "întregi" aplicaţia; ni se pare util să facilităm utilizatorului posibilitatea de a insera alături de <canvas>-ul care conţine graficele un "comentariu didactic" asupra funcţiilor reprezentate (de genul: "elipse tangente unor hiperbole", sau mai amănunţit) şi posibilitatea de a "tipări" apoi rezultatul final, într-o pagină separată.
vezi Cărţile mele (de programare)