Pentru programele care urmează am plecat de la ideea că diferenţa de pătrate caracterizează hiperbola - ecuaţia "redusă" a acesteia fiind x2 - y2 = 1; dar între altele, evidenţiem (prin imitaţie) algoritmul pe care se bazează funcţia image() şi continuăm să ne lămurim asupra unei chestiuni din [1] (transformarea unei imagini existente, prin aplicarea unei funcţii de variabilă complexă).

Următoarea funcţie returnează diferenţa pătratelor vectorilor primiţi ca parametri (sau eventual, valorile "modulo n" ale acestei diferenţe):

hypMod <- function(u, v, modulo=NULL) {
  if(is.null(modulo)) return(u^2 - v^2)
  (u^2 - v^2) %% modulo
}

Ne interesează cazul când vectorii iniţiali reprezintă cele două baze (orizontală şi verticală) ale unei reţele de puncte (v. [1]) - cu alte cuvinte, vizăm diferenţele respective pentru oricare abscisă indicată în primul vector şi oricare ordonată indicată în al doilea. Putem folosi outer(), pentru a aplica funcţia de mai sus pe oricare pereche de valori ale vectorilor respectivi; de exemplu:

> x <- 1:3; y <- c(2, 5)
> (H <- outer(x, y, FUN = hypMod))
     [,1] [,2]  # liniile sunt indexate după 'x', coloanele după 'y'
[1,]   -3  -24
[2,]    0  -21
[3,]    5  -16  # H[3, 2] = x[3]^2 - y[2]^2 = 3^2 - 5^2 = -16

Secvenţa de program următoare produce figurile dedesubtul ei (evident, redarea programului este mult mai simplu de făcut decât explicarea ulterioară a lui…):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

require("RColorBrewer")
col_pal <- brewer.pal(6, "Paired")
x <- y <- seq(-10, 10, 1)
z <- outer(x, y, FUN=hypMod)
opar <- par(mfrow = c(2, 2), mar=c(1.5,0.5,0,0), bty="n", xaxt="n", yaxt="n") 
image(x, y, z, col=col_pal, useRaster=TRUE, asp=1)
mtext("Fig.1a", side=1, line=0.25)

image(x, y, z, col=col_pal, useRaster=TRUE, asp=1)
contour(x, y, z, add=TRUE, drawlabels=FALSE)
mtext("Fig.1b", side=1, line=0.25)

x <- y <- seq(-5, 5, 0.1)
z <- outer(x, y, FUN=hypMod)
mesh <- expand.grid(x=x, y=y)
mesh$z <- c(z)
mesh$col <- cut(mesh$z, 13, labels=FALSE)
plot(mesh$x, mesh$y, col=mesh$col, cex=0.3, pch=19)
mtext("Fig.1c", side=1, line=0.25)

pt <- seq(-pi/2+0.001, pi/2-0.001, by=0.001)
z <- 1/cos(pt) + 1i*tan(pt)  # (1/cos(t), tan(t)) parametrizează x^2-y^2=1
plot(c(z, -z), type="l", xlim=c(-pi, pi), ylim=c(-pi,pi), col="firebrick2")
par(new = TRUE)
plot(c(2*z, -2*z), type="l", xlim=c(-pi, pi), ylim=c(-pi,pi), col="navy")
abline(0, 1, lwd=0.5); abline(0,-1, lwd=0.5); grid()
mtext("Fig.1d", side=1, line=0.25)
par(opar)

dev.copy(png, 'fourim.png'); dev.off()

Funcţia image(x, y, z, col, ...) (apelată în linia 6) partiţionează valorile din 'z' (în care am obţinut prin linia 4, toate diferenţele dintre pătratul unei valori din 'x' şi cel al unei valori din 'y') într-un număr de intervale egale determinat de lungimea vectorului de culori specificat în parametrul 'col' şi apoi cartografiază punctele (x, y) în mici regiuni dreptunghiulare colorate în culoarea indicată prin partiţia constituită în 'z'.

A rezultat astfel Fig.1a. Aplicând - prin linia 10 - şi funcţia contour(x, y, z, ...), ajungem la Fig.1b - pe care putem acum recunoaşte că "punctele" la fel colorate corespund ramurilor unei hiperbole şi celor ale conjugatei acesteia. De altfel, prin secvenţa de linii 21-27, am adăugat şi Fig.1d - pe care am reprezentat două hiperbole echilatere, folosind în linia 22 parametrizarea x = 1 / cos(t), y = tan(t) (care satisface ecuaţia x2 - y2 = 1).

Fig.1c a rezultat prin secvenţa 13-19, în care am imitat algoritmul pe care am încercat să-l descriem mai sus (bazându-ne pe informaţiile afişate prin help(image)), pentru funcţia image(). Prin linia 15 obţinem (apelând expand.grid()) o structură de date "data.frame" conţinând toate perechile de valori 'x', 'y'; în linia 16 adăugăm şi coloana 'z', care conţine din linia 14 toate diferenţele de pătrate - iar în linia 17 adăugăm şi coloana "col", în care folosind funcţia cut(), categorisim valorile din coloana 'z' în 13 intervale de valori (de o aceeaşi lungime). Apoi, prin linia 18, plotăm punctele de coordonate ($x, $y) angajând culorile existente în paleta implicită de culori, la indecşii 1..13 indicaţi de coloana $col.

Am ales să distribuim valorile 'z' în 13 intervale, fiindcă (experimentând prin funcţia table() pe structura de date rezultată în linia 17) am constatat că - pentru vectorii 'x' şi 'y' definiţi în linia 13 - tocmai în acest caz (şi nu cu mai puţine intervale) avem "cea mai bună" repartizare: pe fiecare ramură a unei aceleiaşi hiperbole avem un acelaşi număr de "puncte" (cu aceeaşi valoare 'z').

În liniile 3 şi 13 am constituit o reţea dreptunghiulară de puncte (şi am putut folosi parametrul 'useRaster' în apelul image() - asigurând evitarea unor "necazuri", precum apariţia pe imagine a unei linii albe); dar putem construi imagini similare celor obţinute astfel şi dacă alegem să generăm o reţea aleatorie de puncte (mărind însă, numărul acestora):

x <- sort(runif(2000, -3.5, 3.5))
y <- sort(runif(2000, -3.5, 3.5))
z <- outer(x, y, FUN=hypMod, mod=2)
opar <- par(mar=c(0,0,0,0), bty="n", xaxt="n", yaxt="n")
image(x, y, z, col=brewer.pal(6, "Accent"), asp=1)
par(opar)

Valorile din vectorul 'x' nu mai sunt acum, echidistante (fiind repartizate aleatoriu, prin funcţia runif(); desigur, puteam folosi la fel de bine sample() - obţinând valori distribuite "normal", în loc de "uniform"); ca urmare, nu am mai putut beneficia de 'useRaster' (şi pe imaginea alăturată mai sus se poate sesiza defectul apariţiei a două linii albe).

Pentru decoraţiunile următoare, meritul principal revine algoritmilor din image() şi contour():

Desigur, a trebuit să experimentăm pe diverse reţele (dreptunghiulare) de puncte, cu un set de culori sau cu altul şi cu diverse modulări sau chiar modificări ale formulei de calcul din hypMod() (alegând pentru ilustrare aici, tocmai aceste trei imagini). Intervalul de bază este [-18, 18] pentru primele două imagini şi [-12, 12] pentru ultima, pasul reţelei fiind 0.5; valoarea parametrului 'modulo' este 12 pentru primele două imagini şi 2 pentru ultima - dar în cazul acesteia, am folosit o funcţie hypMod() modificată, returnând u4 - v4. A doua imagine diferă de prima numai prin faptul că pentru a doua am folosit şi parametrul 'col' în apelul funcţiei contour() - specificând chiar 16 culori (îmbinând paletele "Acccent" şi "Set2" ale pachetului "RColorBrewer") - şi în plus, am setat lăţimea liniei la 1.2 (prin parametrul 'lwd').

Pe lângă asemenea decoraţiuni complicate, putem obţine şi imagini mai simple - pentru care am putea investiga fişierul corespunzător (de exemplu, pentru a ne lămuri cum putem aplica unei imagini existente, transformări precum cele din [1]). Avem imediat o "tablă de şah", prin:

x <- y <- 1:8
z <- outer(x, y, FUN=hypMod, mod=2)
opar <- par(mar=c(0,0,0,0), bty="n", xaxt="n", yaxt="n")
image(x, y, z, col=c("gray80", "white"), useRaster=TRUE, asp=1)
par(opar)

Într-adevăr, o tablă de şah este încă o "decoraţiune hiperbolică": paritatea sumei dintre rangul liniei şi cel al coloanei (prin care stabilim în mod uzual, culoarea "alb" sau "negru" a câmpului) poate fi exprimată şi ca paritatea diferenţei pătratelor dintre rangurile respective.

Salvăm imaginea respectivă într-un fişier PNG; nu ne interesează să investigăm fişierul ca atare, ci doar să vedem cum putem reflecta în memorie conţinutul său, pentru a-l folosi în diverse alte prelucrări. Prin png::readPNG() putem încărca fişierul, obţinând o structură de date de tip "array", cu 3 dimensiuni, care poate fi utilizată apoi ca şi matricele obişnuite:

> board <- png::readPNG("decor4.png")  # din pachetul "png" (presupus instalat)
> dim(board)
[1] 480 480   3  # 480x480 pixeli, fiecare cu (R, G, B)
> board[1,1,]
[1] 1 1 1  # celula (1, 1) are R=G=B = 1 (alb, "#FFFFFF")
> board[1,61,]
[1] 0.8 0.8 0.8  # pixelul (1, 61) este colorat cu "#CCCCCC"
> a3b4 <- board[121:255, 121:255, ]  # câmpurile a3-4, b3-4 şi câte 1/4 din b2 şi c3
> plot(0,0, type="n", xlim=c(1,8), ylim=c(1,8), bty="n",
       xaxs="i", yaxs="i", xlab="", ylab="",asp=1)
> rasterImage(a3b4, 1, 2.75, 3.25, 5, interpolate=FALSE)  # afişează "raster"-ul

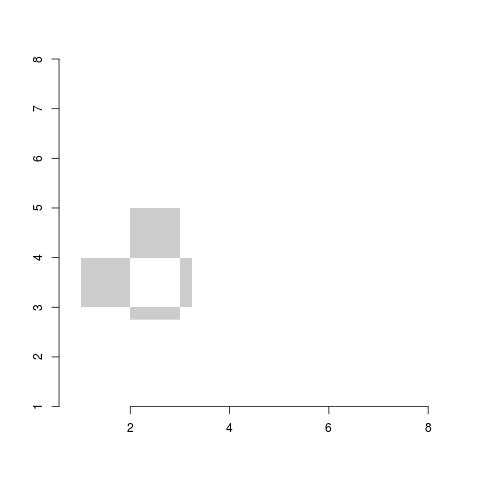
Fiecărui câmp îi corespund câte 60 × 60 pixeli (având 480 / 8 = 60) şi putem selecta (şi putem plota, de exemplu prin rasterImage()) orice regiune dorim (indicând indicii de linie şi coloană ai pixelilor din tabloul respectiv, cum am exemplificat în secvenţa şi imaginea redate mai sus).

Experimentul următor arată că este destul de uşor - mai simplu decât ne aşteptam în [1] - să aplicăm pe o imagine existentă (citită ca mai sus, dintr-un fişier PNG) o transformare sau alta:

x <- y <- 1:480
mesh <- outer(x, y, function(u, v) u + 1i*v)
zone <- mesh[121:255, 121:255]
tsvet <- as.raster(board[121:255, 121:255, ] - 0.5)
plot(0,0, type="n", xlim=c(-480,480), ylim=c(-480,480), 
     bty="n", xlab="", ylab="", asp=1)
points(c(zone, -1.5*zone, cos(zone/45), 100000/zone, 
         -90000/zone), col=tsvet, cex=0.2)
grid()

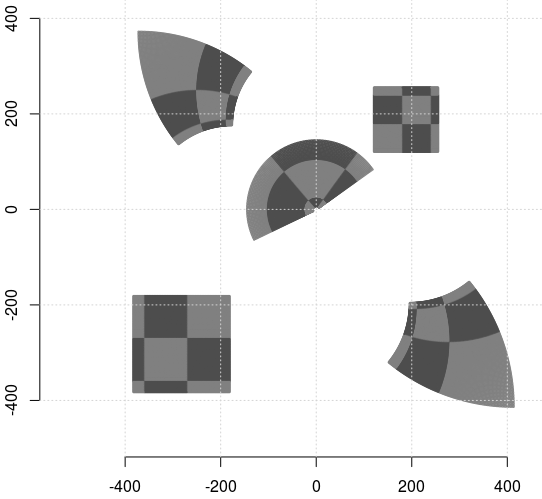
În variabila 'mesh' am constituit o reţea de puncte (numere complexe), reprezentând spaţial - prin coordonate, nu şi prin culoare - pixelii din imaginea respectivă; în 'zone' am selectat afixele pixelilor corespunzători câmpurilor a3, a4, b3, b4 şi la câte un sfert (cel superior, respectiv cel stâng) din câmpurile aflate dedesubtul şi respectiv, la dreapta acestora (plus prima pătrime din sfertul superior al câmpului c2).

Apoi, am selectat din structura 'board' (în care citisem anterior imaginea) câmpurile "R, G, B" corespunzătoare pixelilor din 'zone', am redus cu 0.5 valorile respective (încât să putem distinge mai bine culorile câmpurilor de culoarea fundalului) şi folosind funcţia de conversie as.raster(), am obţinut în variabila 'tsvet' o matrice de tip 135×135 (fiindcă 255-120=135) în care fiecare element este notaţia hexazecimală a culorii câte unuia dintre pixelii respectivi (diminuată "cu 0.5", faţă de cea iniţială - devenind "#808080" pentru "alb" şi "#4D4D4D" pentru "negru").

Am setat fereastra grafică (alegând axele între -480 şi +480) şi în final, am plotat (prin points()) regiunea 'zone', precum şi unele transformări ale acesteia: mărire de 1.5 ori şi răsturnare faţă de originea sistemului de axe (echivalentă cu schimbarea semnului afixelor), apoi transformarea prin funcţia complexă cos() (după scalarea afixelor respective cu factorul 1/45) şi inversarea, cu şi fără răsturnare (alegând însă factori multiplicativi mari, pentru asigurarea lizibilităţii).

Desigur, n-am fi avut nevoie să căutăm factorii de scalare menţionaţi mai sus, dacă alegeam să plotăm regiunile respective în panouri separate (lăsând setarea axelor pentru fiecare panou, în seama funcţiilor de plotare).