În §9.6-9.8 din [1] am vizat împreună atât mediile finale cât şi notele probelor; dar în principiu - fiindcă media finală rezultă direct din notele probelor - ar trebui să vizăm separat notele la una sau mai multe probe şi respectiv, mediile finale. Desigur, avem mereu de înţeles "ce spun" datele respective (interpretând eventual graficele asociate).

Ne ocupăm acum numai de mediile finale - o să le numim note, folosind "medie" doar în sensul statistic; vrem să estimăm densitatea acestora de-a lungul intervalului [5, 10] şi să vedem dacă distribuţia lor este apropiată - că aşa se cuvine şi aşa aşteptăm - de o distribuţie normală.

Să revedem întâi valorile sumative principale:

summary(bac5$Medie)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA 
   5.00    6.73    7.80    7.73    8.75   10.00   50638  
   - - - 25% - - - 50% - - - - - - 75% - - 100%   # 30% sub 5, sau Absent/Eliminat

25% dintre note (cele peste 5, fiindcă valorile 'NA' au fost ignorate de summary()) sunt între 5 şi 6.73 (care este "prima quartilă", Q1), 25% între Q1 şi 7.80 (care este Q2, sau mediana valorilor), 25% între Q2 şi Q3=8.75 şi 25% între Q3 şi 10; media valorilor ("mean") este 7.73 şi fiind ceva mai mică decât mediana - intuim deja că valorile respective sunt distribuite asimetric, cu o plajă spre stânga medianei ceva mai întinsă faţă de coada (mai abruptă) spre mediile mai mari ca mediana.

Selectăm din "bac5" numai datele care ne interesează - judeţul şi mediile diferite de 'NA':

note <- subset(bac5, !is.na(Medie), select = c("Cand", "Medie", "jud"))

Cel mai folosit instrument pentru a estima şi a vizualiza densitatea valorilor este histograma. Am modelat şi noi aşa ceva - v. Histograme - şi avem acum un prilej de a-l folosi pentru un număr mare de valori; întâi trebuie să obţinem lista notelor respective:

write.table(t(note$Medie), file="mediiBac.csv", 
            col.names=FALSE, row.names=FALSE, sep=",")

Am folosit t() pentru a transpune coloana 'Medie' - rezultând o "linie" cu 118301 coloane; nu am folosit mai direct (dar inflexibil) write.csv(), fiindcă aceasta ar fi înscris în fişier şi un antet în care ar denumi coloanele respective (ca "V1", "V2", ..., "V118301") - pe când, write.table() ne permite să ignorăm numele coloanelor (trebuind să indicăm separatorul dorit).

Problema acum este de a selecta linia respectivă din fişierul în care am obţinut-o, urmând să o copiem în "clipboard" şi să pastăm în caseta existentă în fereastra browserului; în acest scop, încărcăm fişierul respectiv în Emacs (alte editoare de text au tendinţa să se blocheze pe liniile de text prea lungi) şi după operaţia "Copy&Paste" indicată, obţinem în browser:

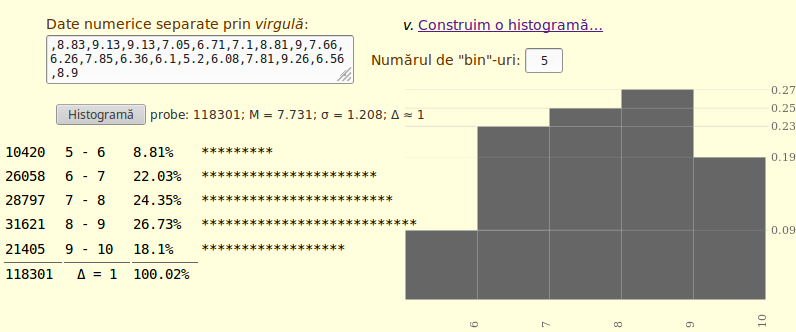
Imaginea redată este preluată din fereastra browserului după ce am lansat programul din Histograme (dar am modificat puţin sursa HTML a aplicaţiei, încât diviziunile să fie poziţionate cum se vede) şi am pastat în caseta respectivă conţinutul fişierului de note obţinut mai sus; am ales 5 ca număr de "bin"-uri, fiindcă astfel avem imaginea distribuţiei notelor pe intervalele standard [5, 6), [6, 7) etc. şi putem face o comparaţie cu ceea ce ştim din [1].

Se confirmă într-o anumită măsură, intuiţia de asimetrie formulată mai la început: avem un vârf pe intervalul [8, 9), faţă de care valorile se întind mai mult spre stânga, decât spre dreapta. Aplicaţia javaScript menţionată avea totuşi caracter didactic, cu parametri expeditivi (şi referiţi la "pixeli") - încât valorile procentuale afişate diferă puţin faţă de cele (cu siguranţă mai precise) pe care le-am obţine folosind de exemplu funcţia pergaps() din [1] §9.6:

pergaps(bac5)[[1]][c(1, 5)]  # v. [1], §9.6
   gap Medie
 [5,6)  8.44  # în aplicaţia javaScript: 8.81% (procentul notelor din intervalul [5, 6))
 [6,7) 22.03  # la fel: 22.03%
 [7,8) 24.29  # 24.35%
 [8,9) 26.64  # 26.73%
[9,10] 18.61  # 18.1%

Acum să obţinem în R, o histogramă:

hist(note$Medie, breaks = "FD", probability = TRUE, right = FALSE)
grid()

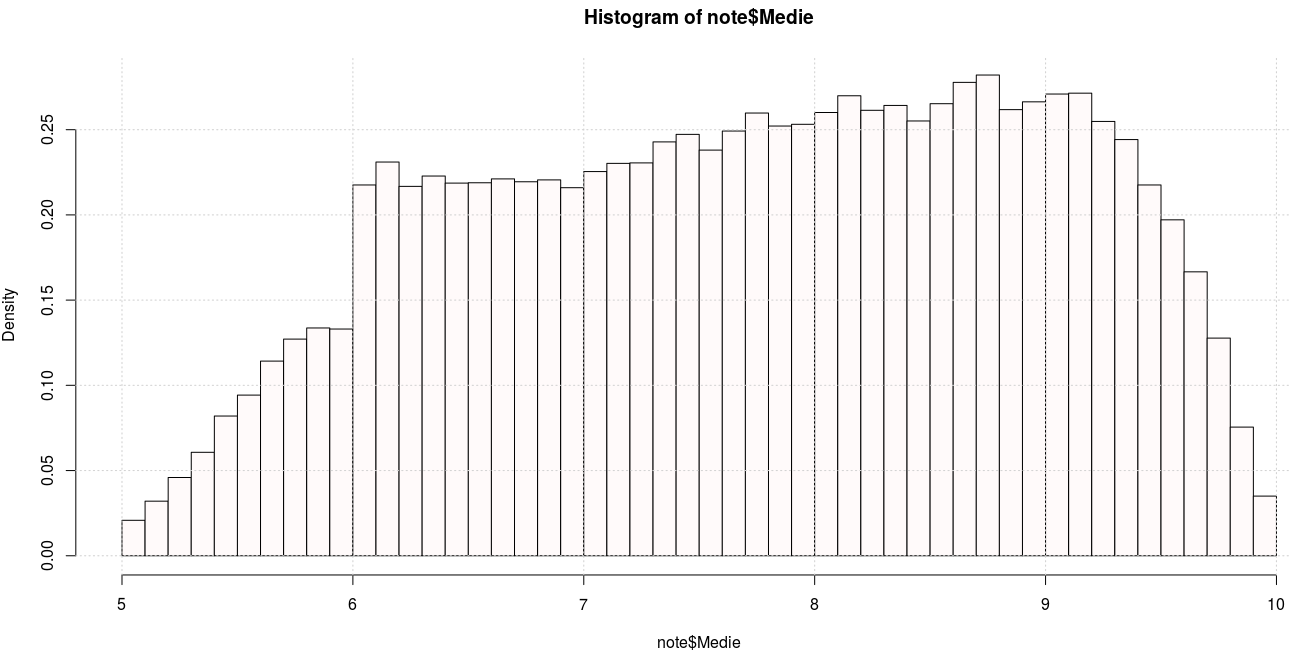
Dintre opţiunile posibile, am ales "FD" pentru parametrul 'breaks' - astfel că lăţimea "bin"-urilor s-a calculat după regula 2 × IQR(x) / n1/3, unde x este vectorul dat, n este lungimea acestuia, iar IQR = Q3 - Q1 este lungimea intervalului în stânga şi în dreapta căruia se află câte 25% dintre valori (diferenţa dintre a treia şi prima quartilă); în cazul nostru IQR = 8.75 - 6.73 = 2.02 şi n = 118301, încât formula redată ne dă valoarea 0.0823 ≈ 0.1 - rezultând (prin rotunjire la "valori frumoase") celule cu lăţimea 0.1 (câte 10 pe fiecare dintre cele 5 intervale de lungime 1).

De fapt, funcţia hist() construieşte şi returnează o listă care ambalează vectorul intervalelor pe care trebuie contorizate valorile date, vectorul frecvenţelor absolute şi vectorul densităţilor (iar redarea grafică este "efectul lateral" asociat în mod implicit):

hist(note$Medie, breaks = "FD", right = FALSE) -> hst
hst$breaks  # capetele intervalelor pe care se înalţă celulele histogramei
 [1]  5.0  5.1  5.2  5.3  5.4  5.5  5.6  5.7  5.8  5.9  6.0  6.1  6.2  6.3  6.4
[16]  6.5  6.6  6.7  6.8  6.9  7.0  7.1  7.2  7.3  7.4  7.5  7.6  7.7  7.8  7.9
[31]  8.0  8.1  8.2  8.3  8.4  8.5  8.6  8.7  8.8  8.9  9.0  9.1  9.2  9.3  9.4
[46]  9.5  9.6  9.7  9.8  9.9 10.0
hst$counts  # frecvenţa absolută a valorilor, pe fiecare interval
 [1]  246  379  543  718  970 1115 1351 1504 1581 1574 2574 2733 2564 2636 2587
[16] 2589 2616 2596 2609 2555 2667 2724 2727 2873 2925 2816 2948 3073 2983 2995
[31] 3077 3193 3092 3126 3018 3138 3286 3337 3097 3151 3205 3211 3015 2889 2574
[46] 2332 1971 1511  893  414
round(hst$density, 3)  # densitatea valorilor, pe fiecare interval
 [1] 0.021 0.032 0.046 0.061 0.082 0.094 0.114 0.127 0.134 0.133 0.218 0.231
[13] 0.217 0.223 0.219 0.219 0.221 0.219 0.221 0.216 0.225 0.230 0.231 0.243
[25] 0.247 0.238 0.249 0.260 0.252 0.253 0.260 0.270 0.261 0.264 0.255 0.265
[37] 0.278 0.282 0.262 0.266 0.271 0.271 0.255 0.244 0.218 0.197 0.167 0.128
[49] 0.075 0.035

Intervalele vizate sunt închise la stânga şi deschise la dreapta (dar ultimul este închis: [9.9, 10]) - datorită setării right=FALSE. Dăm două exemple de interpretare a datelor redate mai sus: pe intervalul [5, 5.1) avem 246 de note, densitatea acestora fiind 0.021; în intervalul [9.9, 10] avem 414 note, "densitatea" corespunzătoare fiind 0.035 (şi observăm că diferă de "frecvenţa relativă", care este 414/nrow(note) = 414/118301 = 0.00349...).

Pe graficul histogramei redat mai sus, "sare în ochi" că pentru celule vecine, diferenţa de înălţime cea mai mare o avem la cele de baze [5.9, 6) şi respectiv [6, 6.1) (cu densităţile 0.133 şi respectiv 0.218); se ştie că statutul de "promovat" începe de la nota 6, încât saltul aşa de brusc (21.8 - 13.3 = 8.5%) de la pragul superior de "nepromovat" la pragul inferior de "promovat" trădează bunăvoinţa tacită cu care se rezolvă de obicei contestaţiile: dacă a făcut de 5.90, ei cum să nu putem găsi să-i mai dăm undeva încă o zecime de punct, ca să promoveze şi el şi să nu mai aştepte încă un an?! Desigur, nu ajunge "o zecime" - trebuie găsite trei zecimi (fiindcă media finală este media aritmetică a celor trei note la probe) şi uneori, acestea nu pot fi identificate (de obicei, pentru motivul că deja notele iniţiale - mai ales, cele mici - au fost deja încărcate cu suficientă bunăvoinţă).

Histogramele ne permit să răspundem la chestiuni de genul următor: care este probabilitatea ca un candidat ales la întâmplare dintre cei notaţi cu cel puţin 5, să aibă media în intervalul [7, 7.2)? Obţinem un răspuns aproximativ însumând densităţile corespunzătoare intervalelor [7, 7.1) şi [7.1, 7.2) - anume 0.225 + 0.230 = 0.455… dar acest "rezultat" (însemnând 45.5%) este enorm, faţă de ceea ce ştim deja din [1] - unde să fi greşit? Am luat "densităţi" (după numele vectorului 'density' din lista returnată de funcţia hist()) - dar oare densităţi trebuie să însumăm?

Avem o cale simplă şi chiar frumoasă, pentru a ne lămuri lucrurile:

sum(hst$density)  # suma valorilor din vectorul 'density'
[1] 10

Dacă ar fi corect să însumăm densităţi pentru a obţine probabilităţi (cum am făcut mai sus), atunci suma tuturor densităţilor ar însemna probabilitatea ca o notă aleasă la întâmplare, să fie în intervalul [5, 10] - ori toate notele sunt între 5 şi 10, deci probabilitatea respectivă este 1 şi implicit, suma densităţilor trebuia să fie 1 şi nu 10.

Corect era să însumăm nu înălţimile, ci ariile celulelor (produsul dintre densitate şi lăţimea celulei), încât P(7 ≤ Nota < 7.2) = ariaCelulei_[7, 7.1] + ariaCelulei_[7.1, 7.2] = 0.225*0.1 + 0.230*0.1 = 0.0455 - adică: probabilitatea ca un candidat ales la întâmplare dintre cei notaţi cu cel puţin 5, să aibă media în intervalul [7, 7.2) este de aproximativ 4.55%.

Pe histograma obţinută în javaScript aveam marcate frecvenţele relative, însumând desigur 1 (aproximativ); pe cea obţinută prin hist() (cu setarea probability=TRUE) avem marcate densităţile şi în acest caz, suma ariilor celulelor (deci aria histogramei) este 1.

Conturul superior al histogramei reprezintă o funcţie "în scară", discontinuă în capetele de celule; dacă ne imaginăm că lăţimea celulei (aceeaşi aici, pentru toate celulele) tinde la 0, atunci conturul tinde să reprezinte o funcţie continuă cu proprietatea că aria subîntinsă are valoarea 1. O astfel de funcţie - continuă, cu valori pozitive şi având 1 pentru aria subîntinsă - este numită "densitate", sau densitate de probabilitate"; dacă X este o variabilă aleatoare "continuă" (teoretic, Nota poate lua orice valoare din intervalul [5, 10]), reprezentată prin funcţia de densitate f_X, atunci (analog calculului redat mai sus), probabilitatea P(a < X < b) este dată de aria subîntinsă de f_X pe [a, b].

Graficul următor ambalează histograma notelor (cea redată mai sus), o estimare a densităţii notelor (folosind funcţia density()) şi curba de densitate pentru distribuţia normală asociată notelor (folosind funcţia dnorm()):

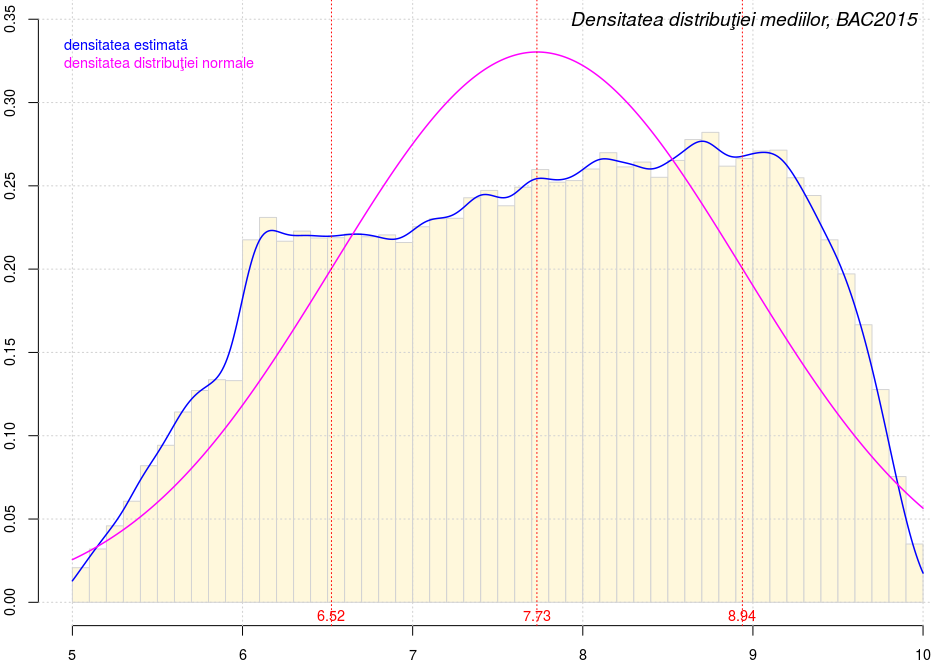
Cele trei linii verticale punctate cu roşu marchează media notelor μ=7.73 - în care distribuţia normală are valoarea maximă, 0.33 - şi limitele abaterii spre stânga (6.52) şi spre dreapta (8.94) cu valoarea deviaţiei standard de la medie (sau "dispersie", σ=1.21); pentru distribuţia normală, în intervalul [6.52, 8.94] se află 68.3% dintre note - ceea ce este cam cu 8.5% mai mult decât în realitatea reprezentată de histogramă. Pe grafic se vede că faţă de distribuţia normală, avem mai multe note sub 6.6 şi mai multe note peste 8.8 (şi mai puţine, între 6.6 şi 8.8).

Am remarcat undeva mai sus că avem un salt brusc (de volum mare) de la notele aflate imediat în stânga lui 6 (care este media minimă necesară pentru a primi "promovat") şi cele aflate imediat în dreapta şi am emis bănuiala că acest salt s-ar datora intervenţiei asupra notelor iniţiale prin rezolvarea binevoitoare a contestaţiilor; dacă acceptăm această presupunere şi dacă o mai extindem şi în partea dreaptă (spre notele mari) - atunci histograma "retrogradată" din cea redată mai sus la notele iniţiale (cele dinaintea rezolvării contestaţiilor), ar avea platoul "orizontal" (între 6.52 şi 8.94) mai îngust şi mai înalt, curgând mai lin şi spre stânga şi spre dreapta. Altfel spus, avem această ipoteză: distribuţia notelor dinaintea contestaţiilor se apropie de distribuţia normală (spre deosebire de cea a notelor finale, cum se vede pe graficul redat mai sus). Ar fi interesant de verificat această ipoteză şi n-am avea decât să recuperăm notele dinaintea contestaţiilor (din fişierul CSV din care am creat în [1] structura de date "bac5") şi să adaptăm şi pentru noile date, demersurile întreprinse mai sus; dar am observat că tocmai s-au postat pe data.gov.ro rezultatele bacalaureatului din 2016, încât aici ne mulţumim să reţinem ipoteza ca atare…

Programul prin care am obţinut graficul de mai sus decurge în maniera uzuală: întâi setăm anumiţi parametri grafici (de exemplu, am mărit suprafaţa destinată graficului - prin reducerea numărului de rânduri lăsate dedesubt, la stânga, etc.), apoi plotăm histograma (prin efectul lateral al funcţiei hist()), prevăzând şi extinderea gradaţiei verticale până la 0.35 (pentru a observa ulterior şi vârful 0.33 al curbei normale), ne ocupăm de curbele de densitate (folosind lines(), nu plot() - pentru ca ele să fie desenate în aceeaşi ferestră grafică în care avem histograma), adăugăm apoi după caz, legende, titluri şi etichete, încheind cu reconstituirea parametrilor grafici impliciţi:

opar <- par(mar=c(2,2,0,0)+0.1, cex.axis=0.9)
    # histograma:
hist(note$Medie, breaks = "FD", probability = TRUE, right = FALSE, 
     col="cornsilk", border="lightgray", ylim = c(0, 0.35), main="")
grid(lwd = 1.1)
    # estimarea densităţii:
dst <- density(note$Medie, from = 5, to = 10, adjust = 0.75)
lines(dst, col="blue", lwd=1.5)
    # densitatea distribuţiei normale N(mf, sf):
mf <- mean(note$Medie)  # media notelor (= 7.730368)
sf <- sd(note$Medie)  # dispersia (= 1.207655)
lines(dst$x, dnorm(dst$x, mean = mf, sd = sf),  lwd=1.5, col="magenta")
    # zona mf ± sf cuprinde 68.27% dintre valori (în distribuţia normală):
abline(v = c(mf-sf, mf, mf+sf), lwd=1, lty="dotted", col="red")
    # legende şi etichetări:
legend("topleft", legend=c("densitatea estimată", "densitatea distribuţiei normale"), 
       text.col=c("blue", "magenta"), bty="n", cex=0.9, inset=c(0, 0.05))
text(c(mf-sf, mf, mf+sf), 0, labels=c(round(mf-sf, 2), round(mf, 2), round(mf+sf, 2)), 
     cex=0.9, col="red", pos=1)
legend("topright", legend="Densitatea distribuţiei mediilor, BAC2015      ", 
       bty="n", text.font=3, cex=1.2)
par(opar)  # reconstituie parametrii grafici standard

Funcţia density() este complicată (şi poate că vom trata în altă parte, elementele KDE din cauza cărora este complicată…). density() returnează un vector obţinut printr-un algoritm care într-o primă fază imită pe cel folosit pentru obţinerea unei histograme - anume, se pleacă de la o divizare a intervalului indicat (de către parametrii from şi to) cu n = 2⁹ (= 512 - în mod implicit) puncte echidistante şi se mai consideră (analog lăţimii "bin"-ului de la histograme) o lăţime de "bandă de netezire" bw (determinată după regula indicată în parametrul 'bw', cu posibilitatea ajustării prin parametrul 'adjust' cum am şi folosit mai sus); apoi, în fiecare dintre cele 512 puncte se generează o distribuţie normală N(μ = punct, σ = bw) - dar pot fi alese şi alte distribuţii de probabilitate, numite generic în acest context "kernel" - centrată în punctul respectiv şi având ca dispersie valoarea bw. Astfel, în fiecare dintre cele 512 puncte s-a creat câte un mic "dâmb" (curba distribuţiei normale), care acoperă şi puncte dintre cele indicate în primul argument al funcţiei (în cazul nostru, cele 118301 note, "puncte" şi ele între gradaţiile 5 şi 10 ale axei orizontale); înălţimea finală în fiecare dintre cele 512 puncte este suma ordonatelor de pe "dâmbul" punctului, corespunzătoare punctelor-note aflate la distanţă de maximum bw de punctul respectiv.

Densitatea de repartiţie a notelor, condiţionată de judeţ

Putem repeta secvenţa redată mai sus, înlocuind 'note' cu restricţia sa la un anumit judeţ sau la un grup de judeţe; dar putem aranja mai uşor şi mai flexibil, datele şi graficele respective, cu un sistem de vizualizare a datelor precum 'ggplot2' (cum am arătat în [1]), sau lattice.

Ne propunem să vizualizăm curbele care estimează densitatea distribuţiei notelor pe fiecare judeţ, în ordinea valorilor mediei judeţene (redată şi aceasta, alături de numele judeţului).

Factorul 'jud' - creat în [1], §5.1 şi preluat din "bac5" în structura de date "note" - are cele 42 de nivele ordonate implicit prin codurile standard (de câte două cifre) ale judeţelor; de exemplu, judeţul "Vaslui" are codul "37" şi ca urmare, "Vaslui" apare pe poziţia a 37-a în vectorul returnat de levels(note$jud), iar pentru elevii din Vaslui câmpul 'jud' are valoarea 37 (înlocuită la afişare, prin "Vaslui"). Următoarea secvenţă reordonează nivelele 'jud' după media pe judeţ (transformând 'jud' în factor ordonat în mod explicit) şi ordonează înregistrările din "note" după acest factor:

note$jud <- with(note, reorder(jud, Medie, FUN = mean, order = TRUE))
note <- note[order(note$jud), ]

Ordonarea după o coloană-factor nu înseamnă intervertirea corespunzătoare a înregistrărilor, ci doar înscrierea în coloana respectivă a indecşilor nivelelor acelui factor; elevii din Vaslui aveau iniţial în coloana 'jud' valoarea 37 - iar acum (dar numai după execuţia celei de-a doua comenzi de mai sus) vor avea valoarea 12 (fiindcă după prima comandă - care ordonează nivelele 'jud' în ordinea crescătoare a mediei pe judeţ - nivelul "Vaslui" are indexul 12).

Vrem să scriem în panoul grafic al judeţului şi media pe judeţ; în lipsa unei idei mai bune (sau mai simple), vom rescrie nivele 'jud', anexând fiecăruia media respectivă:

aggregate(Medie ~ jud, data = note, FUN = mean) -> jud_mean
jud_mean <- jud_mean[order(jud_mean$Medie), ]
levels(note$jud) = paste(levels(note$jud), round(jud_mean$Medie, 2))

Pentru fiecare nivel 'jud', aggregate() a aplicat valorilor care corespund acestuia în coloana 'Medie', funcţia indicată în parametrul 'FUN' (aici, mean()) - returnând un obiect "data.frame" (preluat în variabila 'jud_mean') care conţine 42 de linii, a câte un nume de judeţ şi media aferentă. Am ordonat apoi 'jud_mean' după valorile mediei (crescător) şi în final - am alipit mediile respective (folosind funcţia paste() şi rotunjind la a doua zecimală), nivelelor factorului 'note$jud':

levels(note$jud)
 [1] "Ilfov 7.02"           "Giurgiu 7.26"         "Teleorman 7.41"      
 [4] "Harghita 7.46"        "Călăraşi 7.46"        "Arad 7.49"           
 [7] "Caraş-Severin 7.53"   "Dolj 7.6"             "Bihor 7.61"          
[10] "Constanţa 7.63"       "Ialomiţa 7.63"        "Vaslui 7.64"         
[13] "Argeş 7.65"           "Covasna 7.66"         "Hunedoara 7.68"      
[16] "Maramureş 7.68"       "Gorj 7.68"            "Olt 7.69"            
[19] "Satu-Mare 7.71"       "Mureş 7.71"           "Sălaj 7.72"          
[22] "Timiş 7.72"           "Bistriţa-Năsăud 7.73" "Buzău 7.73"          
[25] "Galaţi 7.74"          "Mehedinţi 7.75"       "Brăila 7.75"         
[28] "Suceava 7.75"         "Dâmboviţa 7.76"       "Vâlcea 7.77"         
[31] "M.Bucureşti 7.77"     "Botoşani 7.81"        "Tulcea 7.81"         
[34] "Sibiu 7.83"           "Neamţ 7.83"           "Bacău 7.84"          
[37] "Braşov 7.84"          "Vrancea 7.84"         "Cluj 7.89"           
[40] "Prahova 7.9"          "Alba 7.94"            "Iaşi 7.95"           

Pe lista obţinută vedem că mediile judeţene intră toate, în intervalul (7, 8); se cuvine să amânăm puţin redarea distribuţiei notelor pe fiecare judeţ, pentru a vedea întâi cum arată distribuţia mediilor judeţene, obţinute mai sus în structura de date 'jud_mean'. În acest nou scop, putem folosi direct - ca mai sus pentru 'note' - density(jud_mean$Medie); dar (pregătind terenul şi pentru scopul principal anunţat) vom folosi lattice::densityplot():

require(lattice)
densityplot(
    jud_mean$Medie,
    from = 7, to = 8, n = 128,
    aspect = "xy",
    main = list(label = "Distribuţia mediilor judeţene (BAC 2015)",
                font = 3, col = "cornsilk4")
) -> dst_list  # structură de date cu toate setările necesare trasării graficului
plot(dst_list)

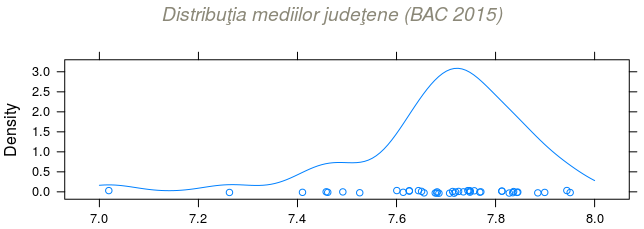
Mediile judeţene sunt marcate prin cerculeţe, deasupra axei orizontale (cel mai din stânga reprezintă "Ilfov 7.02", cel mai din dreapta - "Iaşi 7.95") şi se vede că majoritatea mediilor judeţene sunt "înghesuite" între 7.6 şi 7.85.

Cel mai convenabil este să folosim un fişier "dst_plot.R", pentru secvenţe de comenzi precum cea redată mai sus - executarea secvenţei fiind asigurată de comanda '> source("dst_plot.R")', introdusă la promptul consolei R; astfel, putem formula pe mai multe linii şi nu va trebui să rescriem comenzile la prompul consolei, în cazul (frecvent) în care modificăm sau completăm parametrii.

Desigur că trebuie să parcurgi "în mare" unele documentaţii - de exemplu, folosind comanda 'help(densityplot)' - dar după aceea, când ai nevoie pe parcursul lucrului să vezi sau să-ţi aminteşti ce parametri poţi folosi, cel mai comod şi eficient va fi să inspectezi structura de date obţinută:

str(dst_list)  # listează structura datelor
List of 45
 $ formula          :Class 'formula'  language ~Medie
# ... ... ... #
 $ panel.args.common:List of 1
  ..$ darg:List of 5
  .. ..$ give.Rkern: logi FALSE
  .. ..$ n         : num 128
  .. ..$ from      : num 7
  .. ..$ to        : num 8
  .. ..$ na.rm     : logi TRUE
 $ panel.args       :List of 1
  ..$ :List of 1
  .. ..$ x: num [1:42] 7.02 7.26 7.41 7.46 7.46 ...  # vectorul mediilor judeţene
 $ packet.sizes     : num 42
 $ x.limits         : num [1:2] 6.93 8.07  # abscisa iniţială şi cea finală
 $ y.limits         : num [1:2] -0.185 3.301  # ordonata iniţială şi cea finală
# ... ... ... #
 $ aspect.ratio     : num 0.247  # raportul dintre înălţimea şi lăţimea panoului 
# ... ... ... #

La o primă documentare aproximativă, nu am luat seama la parametrul "aspect" şi rulând secvenţa de comenzi redată mai sus fără setarea 'aspect = "xy"', am obţinut un panou grafic pătrat (pe orizontală, de la 7.0 la 8.0 şi pe verticală între gradaţiile 0.0 şi 0.3 - avem o aceeaşi distanţă); dar este de recunoscut faptul că n-am conştientizat aspectul de "pătrat" decât după ce am inspectat (cum am redat parţial mai sus) structura 'dst_list' - când (în sfârşit) mi-a atras atenţia parametrul 'aspect.ratio' (avea valoarea 1).

Însă adăugând 'aspect.ratio = 0.5' şi rulând din nou secvenţa respectivă - nu s-a modificat nimic (în 'dst_list' apare din nou valoarea 1 - şi nu 0.5 cum setasem eu - pe parametrul 'aspect.ratio'). Acesta a fost un excelent prilej pentru a înţelege mai bine, cum sunt concepuţi în R parametrii diverselor comenzi; pentru unii parametri sunt permise două variante de setare: fie indicând direct valoarea (varianta comună, cea mai obişnuită), fie indicând printr-un nume, o regulă sau o funcţie prin care să fie calculată intern valoarea concretă respectivă (ne amintim că am întâlnit mai la început, un exemplu pentru a doua variantă - când am creat histograma notelor folosind hist(note$Medie, breaks = "FD",...) unde "FD" precizează o regulă de calcul pentru 'breaks').

După ce am luat aminte la aceste aspecte, lucrurile s-au clarificat: 'aspect.ratio' este valoarea internalizată, în urma setării parametrului 'aspect' fie direct (prin 'aspect = 0.5', de exemplu), fie indirect - indicând una dintre regulile de calcul prevăzute: 'aspect = "xy"' (care conduce intern la valoarea 0.247 pentru 'aspect.ratio' - cum se vede prin listarea structurii, redate mai sus).

Pentru regula "xy" calculul decurge aproximativ aşa: se raportează vectorul diferenţelor de ordonate la cel al diferenţelor de abscise, pentru punctele consecutive pe curba care trebuie reprezentată - cu alte cuvinte, se determină pantele secantelor care unesc puncte vecine; se calculează apoi mediana vectorului-raport rezultat şi se alege astfel raportul 'aspect.ratio' încât valoarea mediană rezultată pentru pantele secantelor, adaptată acestui raport (scalată), să fie cât mai apropiată de 1 (panta 1 corespunzând unghiului de 45°).

Revenim acum la problema principală - să vizualizăm curbele care estimează densitatea distribuţiei notelor pe fiecare judeţ:

require(lattice)
densityplot(
    ~ Medie | jud,  # densitatea notelor, pe fiecare judeţ în parte
    data = note, 
 #  subset = as.numeric(jud) %in% c(8, 10, 13, 26),  # pentru un grup de judeţe
    from = 5, to = 10, n = 128,  # pentru calculul densităţii
    type = "g", aspect = 0.5,  # grid, înălţime/lăţime=0.5
    par.strip.text = list(cex=0.8),  # reduce mărimea de scriere a etichetelor
 layout = c(7, 6),  # 6 linii a câte 7 panouri (42 judeţe)
    as.table = TRUE,  # de la stânga la dreapta, de sus în jos
    main = list(label = "Distribuţia mediilor în judeţe (BAC 2015)",  # titlu
                font=3, col="cornsilk4")
) -> dst_list  # listă cu toate datele şi setările necesare trasării graficului
plot(dst_list)

O formulă ca "~ x | f" (în cazul nostru, ~Medie | jud) induce estimarea densităţii variabilei "x" pentru fiecare dintre nivelele factorului "f". Vom obţine astfel 42 de panouri (câte unul pentru fiecare judeţ) şi am folosit parametrul 'layout' pentru a le aranja sub forma unei matrice cu 6 linii şi 7 coloane; cu 'as.table = TRUE' ne asigurăm că panourile vor fi constituite după regula obişnuită - de la stânga spre dreapta şi de sus în jos (ordinea lor fiind aceea stabilită mai devreme în "note", anume ordinea crescătoare a mediilor judeţene):

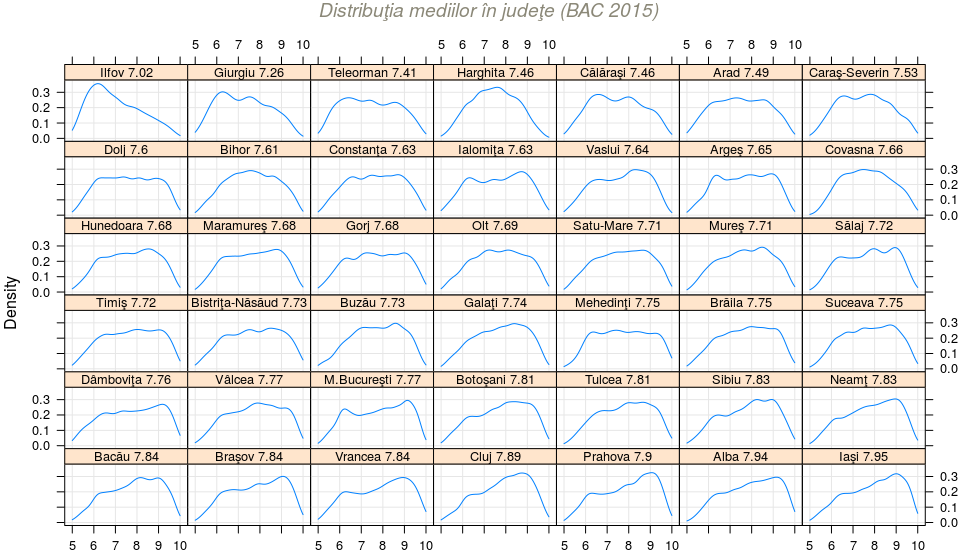
Dacă decomentăm în secvenţa redată mai sus, linia parametrului 'subset', putem obţine curbele respective numai pentru judeţele indicate prin indecşii acestora în vectorul levels(jud); eventual, valorile din 'layout' trebuie adaptate (pentru 8 judeţe de exemplu, n-o să folosim 6 linii şi 7 coloane ca în cazul celor 42). Dăm un exemplu, alegând acele judeţe pentru care densitatea pe intervalul [6, 9] se "aplatizează" mai mult (decât la celelalte), apropiindu-se de o distribuţie uniformă:

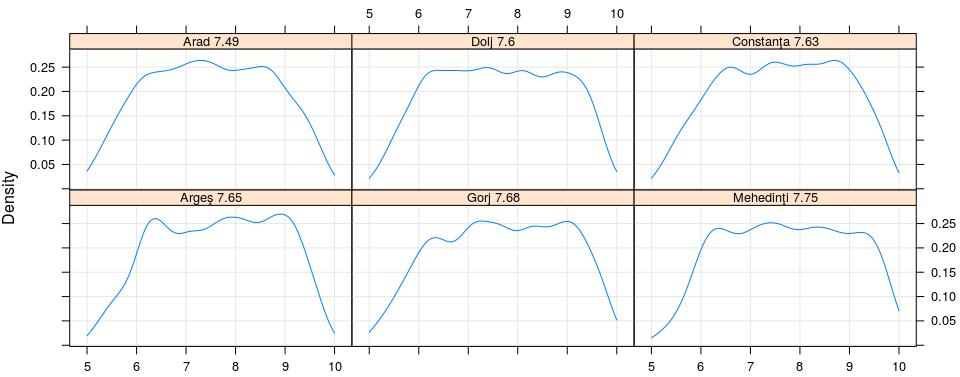
Ce putem zice pe baza graficelor redate - fără a mai folosi alte instrumente - este că în nici unul dintre cazuri, nu avem ca estimare, o distribuţie normală (cum ne aşteptăm, de regulă); avem câte un vârf cu înălţimea aproximativă de 25%-30%, care pe măsură ce media judeţeană creşte (uitându-ne pe cele 42 de grafice de la stânga la dreapta şi de sus în jos), se mută dinspre zona mediilor 6-7 (începând cu "Ilfov 7.02", unde 7.02 este media judeţeană) spre zona mediilor 8-9 (terminând cu "Iaşi 7.95").