Să se rezolve ecuaţia ([1] 2002 - problema 68-5), pag. 250; [2] pag. 86)

De obicei `z` desemnează o variabilă complexă; punctul `1 + iz` (unde `i` este "unitatea imaginară") rezultă prin rotirea lui `z` cu 90° (în jurul originii), urmată de translaţia orizontală cu o unitate.

Ne "deranjează" radicalul de ordin doi din partea dreaptă a ecuaţiei (dacă `n` este impar). De obicei "ridicăm ecuaţia la pătrat" (scăpând de radical), dar astfel pot apărea "rădăcini străine".

În multe culegeri de probleme se vizează un alt "truc" pentru a "scăpa" de radical, bazat pe faptul că `1 + tan ^2 alpha = cos ^(-2) alpha`; din păcate, rostul problemelor respective pare a fi doar evidenţierea trucului menţionat - nicăieri nu se discută posibilitatea (sau imposibilitatea) apariţiei de "rădăcini străine".

Astfel, în [1] la "rezultat" şi în [2] se prezintă această indicaţie de rezolvare:

Dar "`z = tan alpha`" ar însemna `z` `in RR` (nivelul liceal exclude "funcţii complexe") şi am avea o ecuaţie de variabilă reală (în primul membru, "partea imaginară" este de fapt zero) - iar atunci, s-ar pune într-un fel sau altul şi problema rădăcinilor străine.

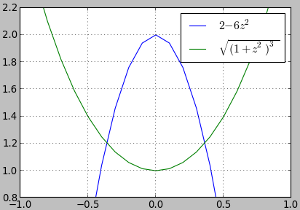De exemplu, pentru `n = 3` am avea de rezolvat peste `RR` ecuaţia `2 - 6z^2 = sqrt((1 + z^2)^3)`. Aceasta nu are decât două rădăcini reale - cum se vede pe graficele funcţiilor reale din cei doi membri; deci patru dintre cele şase indicate la "rezultat" sunt "rădăcini străine": nu satisfac condiţia ca primul membru să rămână pozitiv - condiţie atrasă de limitarea la `RR` a variabilei (şi implicit… a radicalului, considerat ca funcţie reală).

Deci avem de completat indicaţia reprodusă mai sus, subliniind că `z` trebuie considerată ca variabilă complexă, ceea ce asigură pentru radical două valori (ramurile funcţiei complexe "radical") şi… exclude posibilitatea "rădăcinilor străine". Că rezultatul final trebuie corectat (ecuaţia "elementară" `cos t = a` are soluţiile `bb 2 k pi pm ...`) este mai puţin important - ne-am obişnuit cu rezultate greşite, purtate apoi în toate culegerile de probleme.

Se vede (fără calcul efectiv) că dacă ridicăm la pătrat (pentru a "scăpa" de radical) obţinem o ecuaţie polinomială de grad `2n`; aceasta are `2n` rădăcini, reale sau complexe. Deci ecuaţia iniţială are cel mult `2n` rădăcini ("cel mult", fiindcă ridicând la pătrat pot apărea şi "rădăcini străine") şi este posibil ca unele să fie reale, iar altele complexe nereale.

Să încercăm să găsim întâi rădăcinile reale ale ecuaţiei iniţiale. Putem ţine seama de faptul că funcţia tangentă aplică biunivoc (`-pi//2, pi//2`) pe `RR` deci pentru `z``in RR` există unic `alpha``in`(`-pi//2, pi//2`) încât `z = tan alpha` şi avem `1 + z^2 = 1 + tan^2 alpha = cos^(-2) alpha`. Rezultă, succesiv:

[ "rezultatul" dat în [1], [2] este greşit: nu este `tan` `({:k pi:}/n pm pi/{:3n:})`, ci `tan` `({:bb(2) k pi:}/n pm pi/{:3n:})` ].

Numărul de rădăcini reale `z` este dat de numărul de valori `k``in ZZ` pentru care `alpha in`(`-pi/2, pi/2`) şi un calcul elementar ne conduce la:

În fiecare dintre cele două cazuri găsim exact câte `n` astfel de valori `k`. Rezultă că ecuaţia iniţială are exact `2n` rădăcini reale şi nu mai este cazul de a căuta rădăcini complexe nereale (fiindcă am stabilit anterior că ecuaţia respectivă are cel mult `2n` rădăcini, reale sau complexe).

Bineînţeles că ecuaţia se putea rezolva şi altfel, dar cu mai multe calcule: `1 + z^2 = (1 + iz)(1 - iz)` şi cu `u = 1 + iz,\ v = 1 - iz` rezultă ecuaţia omogenă `u^n + v^n = u^(n//2) v^(n//2)`; se obţine `u//v` (cu unele subtilităţi, ţinând cont de paritatea lui `n`), de unde se "scoate" `z`.

Ar mai fi de observat că rădăcinile sunt două câte două opuse (fiindcă în primul membru - dezvoltând binoamele - rămân numai puteri pare de `z`), încât era suficient să le căutăm pe cele cu `alpha in (0, pi/2)`.

Studiul unui caz particular, cu NumPy şi matplotlib

Dacă `n` este par, atunci "ridicarea la pătrat" este chiar inutilă şi putem considera că în acest caz avem `n` rădăcini (dacă `n` este par, radicalul din membrul drept dispare "automat" - avem deja o ecuaţie polinomială de grad `n` şi prin "ridicare la pătrat" doar am dubla zerourile acesteia).

Astfel, pentru `n = 4`, am avea ecuaţia

Putem afla rădăcinile acestui polinom (verificând cele de mai sus) folosind de exemplu NumPy şi putem vizualiza graficul corespunzător folosind matplotlib:

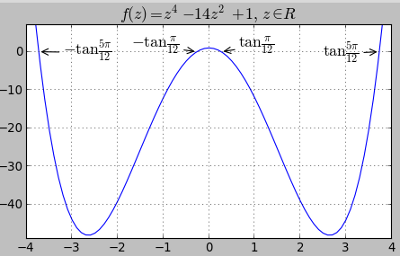
vb@vb:~$ python
>>> 
>>> import numpy as np
>>> polinom = [1, 0, -14, 0, 1]
>>> np.roots(polinom)
array([-3.73205081,  3.73205081, 
       -0.26794919,  0.26794919])
>>> 
>>> from math import pi, tan
>>> print tan(pi/12), tan(5*pi/12)
0.267949192431 3.73205080757
>>> 

Următorul script Python ne-a dat graficul de mai sus, considerând `z` ca variabilă reală (nu complexă); liniile esenţiale sunt 1, 2, 3, 5, 16 - celelalte linii adaugă figurii notări auxiliare (de exemplu, am marcat intersecţiile cu axa y=0):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

from numpy import *
import matplotlib.pyplot as plt
z = arange(-4., 4., 0.1)
plt.axis([-4, 4, -49, 7])
plt.plot(z, z**4 - 14*z**2 + 1)
plt.title(r'$f(z) = z^4 - 14z^2 + 1,\ z \in R$', fontsize=16)
grd = plt.grid(True)
annotations = [[r'$\tan\frac{\pi}{12}$', (tan(pi/12), 0), (0.65, 1)],
               [r'$-\tan\frac{\pi}{12}$', (tan(-pi/12), 0), (-1.7, 1)],
               [r'$-\tan\frac{5\pi}{12}$', (tan(-5*pi/12), 0), (-3.2, -1)],
               [r'$\tan\frac{5\pi}{12}$', (tan(5*pi/12), 0), (2.5, -1.3)]]
for ann in annotations:
    plt.annotate(ann[0], xy = ann[1], xytext = ann[2], 
                 arrowprops = dict(arrowstyle='->'), 
                 fontsize=16) 
plt.show()

Pentru funcţii reale de variabilă reală putem vizualiza toate proprietăţile funcţiei. Polinomul de mai sus este simetric faţă de axa x=0 şi are trei puncte de extrem; calculând derivata, constatăm că minimele au abscisele `pm sqrt(7)`, iar pe grafic vedem că valoarea minimă este apropiată de -50.

Pentru funcţii complexe `bbz = x + iy in D rarr bbw = u(x,y) + iv(x,y), D sub CC` vizualizarea comportării se complică - fiindcă am avea patru dimensiuni: `(x, y, u, v) in RR^4`- şi o soluţie (apărută după 1990 şi utilizată curent în "grafica digitală artistică") implică spaţiul culorilor.

Principiul este următorul: se "pictează" planul `bbw` fie utilizând o anumită formulă sau funcţie care asociază fiecărui punct o anumită culoare, fie angajând direct un gradient de culoare (fie… încărcând chiar o imagine propriu-zisă - ceea ce poate fi mai interesant); apoi, se colorează fiecare punct `bbz` (din domeniul funcţiei respective) cu acea culoare care a fost asociată imaginii `bbw` a acelui punct.

Cel mai simplu, putem obţine o astfel de reprezentare folosind pachetul mpmath:

from mpmath import *
cplot( lambda z: z**4 - 14*z**2 + 1, [-5,5], [-3,3], points=10000 )

Harta polinomului `f(z) = z^4 - 14z^2 + 1,\ z in CC`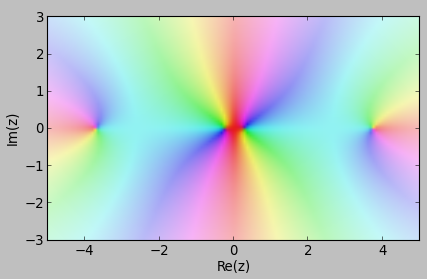
	Gradientul folosit (harta funcţiei `f(z) = z`)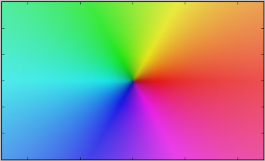

Pentru a "citi" pe reprezentarea obţinută proprietăţile funcţiei respective, trebuie să cunoaştem schema de colorare care s-a folosit pentru "planul-`bb w`". Gradientul respectiv se poate vizualiza plotând funcţia identitate (prin cplot(lambda z: z, [-5,5], ...); dar pentru "exactitate", ar trebui implicat acelaşi domeniu şi acelaşi număr de "points" ca pentru funcţia reprezentată.

Am redat mai sus (dar micşorând imaginea) gradientul standard folosit de mpmath (rezultat prin modulul Python colorsys); încă se disting gradaţiile domeniului (de la -5 la 5 pe axa reală şi de la -3 la 3 pe cea imaginară). Vedem că numerele reale pozitive (adică numerele complexe de argument 0°) sunt colorate cu roşu - din ce în ce mai închis spre zero şi din ce în ce mai deschis spre infinit; analog este folosită culoarea cyan, pentru numerele reale negative (de argument 180°).

Mai general, culoarea roşie este degradată treptat (către galben) pe măsură ce unghiul indicat de `arg(z)` creşte de la 0° la 60°; la fel, când unghiul creşte în sens orar - de la 0° la minus 60° - dar de această dată roşu este "degradat" către magenta. Analog pentru unghiuri de la 60° la 120° (de la galben spre verde şi apoi către cyan), ş.a.m.d. Nuanţele de culoare reflectă valorile argumentului, iar strălucirea corespunde modulului valorilor complexe ale funcţiei (a vedea HSV color).

Pentru polinomul a cărui "hartă" am redat-o mai sus, avem `f(0) = 1, f(i) = 16` şi mai general, `f(lambda i)` pentru `lambda in RR` sunt valori reale pozitive ("proporţionale" cu `lambda`) - astfel că toate punctele de pe axa imaginară sunt colorate pe "hartă" cu roşu (ca şi axa reală pozitivă de pe "gradient"), din ce în ce mai palid ("proporţional" cu distanţa la origine).

Rădăcinile polinomului se disting prin faptul că în jurul punctelor respective "gravitează" toate culorile gradientului (la fel ca în originea imaginii "gradient"; intervine aici faptul că argumentul numărului complex zero este nedeterminat). Avem `f(1) = -12`, deci pe "hartă" punctul (1, 0) este cyan (ca şi punctele semiaxei reale negative de pe "gradient").

Secţionând harta după axa reală Im(z) = 0 - deducem comportamentul descris de graficul funcţiei pentru cazul `z` `in RR` (grafic redat ceva mai sus): de la -5 spre 0 avem secvenţa de culori roşu din ce în ce mai accentuat (adică "valori pozitive descrescătoare"), zero, apoi cyan din ce în ce mai palid până pe la abscisa -3, de unde începe să se accentueze (ceea ce înseamnă valori negative din ce în ce mai mici, apoi din ce în ce mai mari), apoi zero urmat de roşu din ce în ce mai intens (adică valorile devin pozitive şi cresc).

Pentru încă un exemplu de interpretare a "hărţii": avem `f(1 - i) = -3 + 28i`, deci punctul `1 - i` de pe "hartă" (aflat în cadranul IV, pe diagonala acestuia) este colorat precum punctul `-3 + 28i` (din cadranul II, apropiat de axa verticală) de pe "gradient" - astfel că îi revine o nuanţă de verde.

Nu putem preciza exact culoarea, fiindcă punctul (-3, 28) nu apare pe "gradientul" redat mai sus (unde sunt reflectate doar punctele din [-5, 5]×[-3, 3]); pentru "exactitate", ar fi trebuit să calculăm marginile codomeniului funcţiei şi să plotăm gradientul `f(z) = z` pe [-5, 5]×codomeniu.

Însă în cazul nuanţelor de culoare nu se poate vorbi de "exactitate" şi trebuie să ne mulţumim cu o percepţie aproximativă… În loc de a căuta "exactitatea", în scopul mai bunei înţelegeri a comportării funcţiei pe baza "hărţii" acesteia - poate fi mai util (ca… alternativă practică faţă de aprofundarea teoretică a domeniului funcţiilor complexe) să replotăm "harta" angajând alte gradiente.

Probabil că ar putea fi concepute scheme de colorare (şi "secţionări" ale hărţii) care să avantajeze una anumită sau alta, dintre caracteristicile comportamentale ale funcţiei. Funcţia mpmath.cplot() invocată mai sus pentru obţinerea "hărţii" acceptă ca parametru şi o funcţie de colorare proprie; dar în loc de a concepe vreo asemenea funcţie şi a replota "harta" prin cplot(), putem prefera calea "artistică" - încărcăm imaginea rezultată mai sus în GIMP şi îi aplicăm câte un alt gradient:

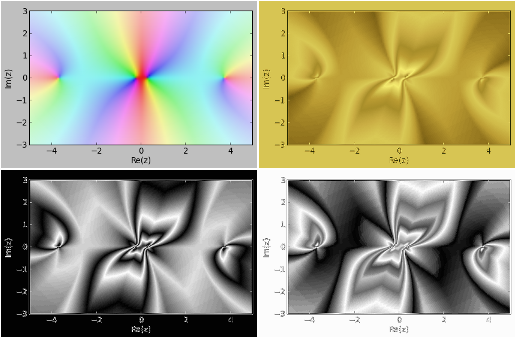
Imaginile care se obţin depind şi de maniera de lucru folosită: după ce vom fi recolorat imaginea (meniul Colors, selectând Map şi apoi Gradient Map) conform gradientului activ (selectat în prealabil din Toolbox) avem în principiu două posibilităţi, cu rezultate foarte diferite: fie aplicăm un alt gradient pe imaginea curentă ("modificată" deja faţă de cea iniţială), fie întâi revenim la gradientul iniţial - şi aşa am procedat în cazul imaginilor redate mai sus - şi apoi probăm un altul.

Am văzut că zerourile lui `f(z) = z^4 -14z^2 + 1` sunt `pm tan {:pi/12:}, pm tan {:(5pi)/12:}` şi rezultă o descompunere de forma `f(z) = (z^2 - c^2)(z^2 - d^2), c,d in RR` - deci unele proprietăţi ale lui `f` se pot deduce din reprezentarea lui `bb(g(z) = z^2 - c^2)`, pentru un `bb c in RR` convenabil; alegând `bb c = 0.64` (ceva mai mare decât `tan {:pi/12:}`, pentru lizibilitate) obţinem folosind math.cplot() şi aplicând gradiente din GIMP:

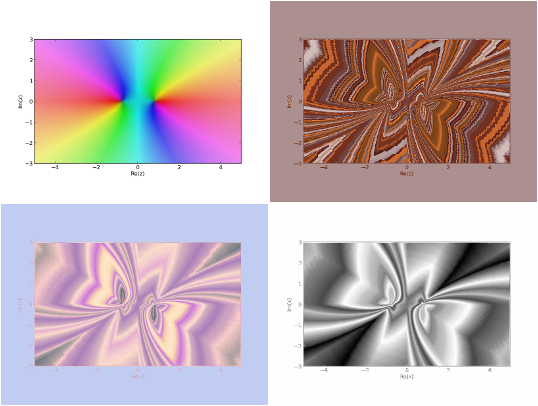
Desigur… până la urmă ar trebui să mai "descoperim" că `g(z) = (z-c)(z+c), c in RR` ajungând la studiul de bază: `h(z) = z + c` - ceea ce înseamnă în fond a o lua de la capăt; dar ideea unui studiu mai temeinic rămâne eventual pentru altă dată.