Pentru funcţii elementare de o variabilă reală poţi preciza dinainte, cam cum va arăta graficul (cel mai banal exemplu: o funcţie "de gradul întâi" are ca grafic o anumită dreaptă). În schimb, doar văzând expresiile pe care se bazează plotarea punctelor - nu prea poţi să anticipezi "graficul" produs pe ecran printr-un program de creaţie grafică (pentru care este caracteristică iterarea şi parametrizarea, cu efecte dificil de prevăzut); cel mult, poţi intui sau estima aspecte generale de mărginire, simetrie şi periodicitate - de exemplu în cazul expresiilor bazate pe funcţii circulare.

Totuşi, o lucrare grafică reuşită (aspectuoasă şi având pe cât se poate, o doză acceptabilă de originalitate) nu rezultă neapărat doar din întâmplare (nimerind nişte expresii şi nişte valori ale parametrilor)… Prezentăm un "experiment" - cam cu tot ce înseamnă aceasta, inclusiv cu greşeli - care conduce la nişte expresii care ne-au permis conturarea câtorva lucrări "reuşite" (folosind plotart() din [1]); expresiile respective sunt departe de a fi "noi", fiind bazate tot pe sin(), cos() (în [2] de exemplu, regăsim combinaţii de câte trei astfel de termeni - discutate şi chestionate succint la un alt nivel faţă de experimentul nostru; noi plecăm de la "adunarea vectorilor" din geometria elementară, aplicată punctelor a două cercuri).

Amintim întâi, câteva lucruri şi legături (puncte, vectori, sin() şi cos(), numere complexe; R).

Orice punct se poate "reprezenta" prin "vectorul de poziţie" al său - vectorul (în sens geometric) cu originea fixată în O(0, 0) şi cu extremitatea în acel punct. Dacă rotim vectorul de poziţie al unui punct dat, în jurul originii - regăsim punctul respectiv după o rotaţie completă (şi cum momentele de timp diferă, putem spune că obţinem un nou punct, suprapus însă peste cel iniţial). Dacă φ măsoară unghiul de rotaţie la momentul curent - faţă de vectorul fixat (1, 0), în sens antiorar - atunci putem reprezenta vectorii de poziţie (sau punctele din plan) prin (x=ρ cos(φ), y=ρ sin(φ)), unde ρ este lungimea vectorului.

Punctul P(x, y) se poate reprezenta şi prin expresia de număr complex x + i y (i fiind "unitatea imaginară", i² = -1), sau ρ(cos(φ) + i sin(φ)) - care se poate scrie mai simplu folosind exponenţiala complexă (introdusă de Euler): ρ ei φ. Astfel, când u variază între 0 şi 2π, expresia R "exp(1i * u)" reprezintă (toate) punctele cercului de rază 1 centrat în origine.

Desigur, nu poate fi vorba de "toate" punctele (fiindcă pentru calculator avem un model aproximativ al numerelor reale); dar tocmai acest defect este la baza obţinerii de imagini specifice pentru "creaţia grafică": dacă s-ar reprezenta toate punctele reale, ar putea rezulta o imagine opacă (înnegrită complet), pe când reprezentându-le cu un anumit pas, putem distinge un eşantion sau altul de pe imaginea reală (putând evidenţia o formă sau alta).

Considerăm pe două (sau mai multe) cercuri concentrice un acelaşi număr de puncte şi însumăm vectorii de poziţie de acelaşi rang - obţinând astfel noi puncte, care eventual pot forma un contur (sau şablon) care să stea la baza generării unei imagini "interesante" (fie prin îndesirea punctelor considerate iniţial, fie iterând construcţia prin deplasarea cu un anumit pas unghiular a punctelor unuia dintre cercuri, fie inventând vreo altă idee de generare, fie… din întâmplare, sau greşeală).

Să observăm că dacă am considera puncte la fel distanţate unghiular şi pe un cerc şi pe celălalt, atunci n-am obţine nimic interesant: suma vectorilor de poziţie de acelaşi rang ar reprezenta (banal) puncte ale unui nou cerc (având ca rază suma razelor cercurilor iniţiale). Deasemenea, dacă am pleca de la puncte generate aleatoriu pe un cerc şi pe celălalt - şansele de a rezulta altceva decât o "aiureală" (fără aspecte de simetrie şi de periodicitate, specifice imaginilor pe care le considerăm toţi ca fiind frumoase) sunt extrem de mici.

Am formulat imaginea următoare printr-un program pe care o să-l redăm (fiind instructiv pentru folosirea limbajului R) ceva mai încolo; avem câte 12 puncte, etichetate cu negru şi respectiv cu albastru - punctele negre fiind distanţate unghiular cu π/6, iar cele albastre cu 3*π/6 (rezultând suprapunerea a câte 3 dintre cele 12 puncte albastre):

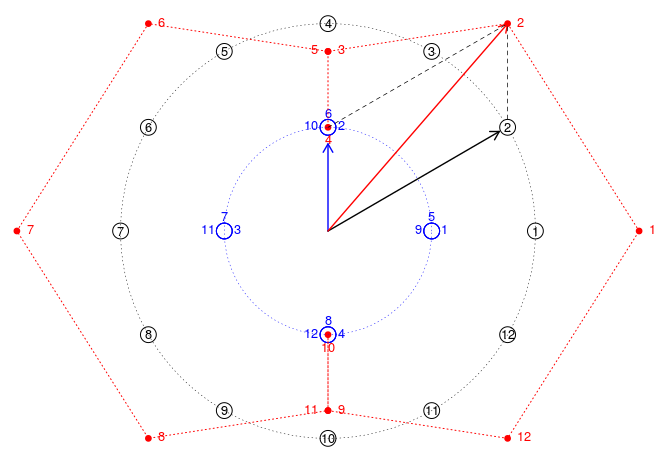
Însumând vectorii de poziţie la fel etichetaţi (1 negru cu 1 albastru, etc.), obţinem punctele marcate şi etichetate cu roşu; pe imagine am evidenţiat operaţia de adunare prin "regula paralelogramului", a vectorilor 2 negru şi 2 albastru (rezultând vectorul "2 roşu"). Nu este cazul să ne cramponăm de aspecte particulare: vârfurile roşii 3 şi 5 rezultă în mijlocul segmentului negru 3-5 (şi la fel 9 şi 11 sunt în mijlocul segmentului 9-11).

Conturul rezultat (marcat prin linie punctată cu roşu) este susceptibil de a fi "interesant": este mărginit (adică poate fi bine încadrat în "teren"), este simetric (dar nu banal, ca în cazul punctelor conciclice) şi buclează spre interior în două locuri (arcul roşu 3-4 este dublat de arcul invers 4-5 şi simetric, arcul 9-10 este întors prin arcul 10-11).

Iată programul (secţionat pe etape şi comentat) prin care am produs pe ecran exact construcţia redată şi discutată mai sus:

ang <- seq(0, 2*pi, pi/6)  # progresie aritmetică de raţie π/6, pe segmentul [0, 2π]
u <- ang[-13]  # fără capătul final 2π
black <- xy.coords(exp(1i*u))  # lista punctelor (cos(u), sin(u)) de pe cercul negru
blue <- xy.coords(exp(1i*3*u)/2)  # punctele (cos(3u)/2, sin(3u)/2) de pe cercul albastru
red <- list(x = black[[1]] + blue[[1]], y = black[[2]] + blue[[2]])  # punctele roşii
           # se însumează "vectorii de poziţie" de acelaşi rang, din 'black' şi 'blue'
# Iniţializează fereastra grafică:
opar <- par(mar=c(0, 0, 0, 0), bty="n", xaxt="n", yaxt="n")
plot.new()
plot.window(xlim=c(-1.5, 1.5), ylim=c(-1.5, 1.5), asp=1)
# Plotează punctele:
points(black, cex=2.2) 
points(blue, cex=2.2, col="blue") 
points(red, cex=1.2, pch=20, col="red")
# Etichetează punctele (cu 1, 2, ..., 12 - pe negru, albastru, respectiv roşu)
text(black, cex=0.8)
text(blue, cex=0.8, col="blue", 
     pos=c(rep(4,4), rep(3,4), rep(2,4)))  # evită suprapunerea etichetelor
text(red, cex=0.8, col="red", pos=c(4,4,4,1,2,4,4,4,4,1,2,4))
# Trasează cercurile care conţin punctele negre şi respectiv, albastre:
a <- seq(0, 2*pi, pi/2000)
lines(exp(1i*a), lwd=0.5, lty="dotted")
lines(exp(1i*a)/2, lwd=0.5, lty="dotted", col="blue")
# Trasează segmentele care unesc puncte roşii consecutive (ca rang):
lines(x=append(red[[1]], 1.5),  # adaugă capătul final (pentru a închide traseul)
      y=append(red[[2]], 0),
      lwd=1, lty="dotted", col="red")
# Ilustrează adunarea vectorilor de poziţie (cu "regula paralelogramului"):
arrows(c(0,0,0), c(0,0,0), c(0,cos(pi/6)-0.04,cos(pi/6)), c(0.42,sin(pi/6)-0.02,1),
       col=c("blue", "black", "red"), length=0.1, lwd=1.4)
segments(c(0, cos(pi/6)), c(0.5, 0.54), c(cos(pi/6), cos(pi/6)), c(1, 1), 
         lty="dashed", lwd=0.7)
# Reconstituie parametrii grafici dinaintea modificării acestora:
par(opar)

Având puncte care se suprapun, ne-am lovit de problema evitării suprapunerii etichetelor acestora; pentru acest caz particular (cu număr mic de puncte) a fost suficient să folosim direct parametrul 'pos' al funcţiei text() - indicând pentru fiecare punct poziţia (dedesubt, la stânga, deasupra, la dreapta) în care să fie plasată eticheta.

Descriu cum au decurs mai departe speculaţiile mele - dar se cuvine să avertizez acum că am o greşeală "de neiertat", pe parcursul acestora (o voi explicita tocmai când - în sfârşit - am sesizat-o!).

Schimbând pasul unghiular π/6 cu π/5, pe cercul albastru nu vom mai avea suprapuneri de puncte (fiindcă acest cerc este parcurs cu pasul 3*u, iar 5 şi 3 nu au divizori comuni); ca urmare, nu vom mai avea arce duble (pe circuitul roşu format astfel, arcul 2-3 vine spre interior, arcul 3-4 este orizontal, iar arcul 4-5 iese spre exterior). Reluând astfel programul (dar renunţând parţial la secţiunea de etichetare a vârfurilor) şi adăugându-i o secţiune de iterare a construcţiei — anume, rotim cele 10 puncte ale cercului albastru cu π/k (folosind expresia exp(1i*3*u + pi/k)/2), unde k parcurge cu pasul 0.1 intervalul [2.75, 6], ales prin încercări) — circuitul roşu se multiplică spre interior, obţinând prima "creaţie" de mai jos; pentru a doua, am folosit pasul unghiular π/9 (pentru care avem iarăşi puncte duble, dar nu şi arce duble) şi am variat k între 3.8 şi 12:

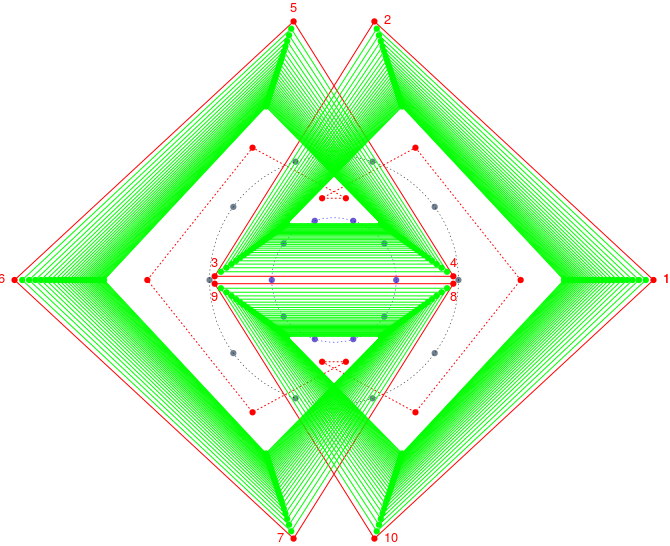
Ca să folosim acum plotart() - "scurtând" măcar, programul cu care am experimentat mai sus - avem nevoie de o funcţie care să determine sumele vectorilor de poziţie pentru fiecare rotire a punctelor unuia sau altuia dintre cele două cercuri:

sum_rotate <- function(from, to, step, circle = 1) {
    sump <- as.complex()
    switch(circle,
         # roteşte punctele cercului 1 (mic) cu π/k şi însumează vectorii (∀k)
          for(k in seq(from, to, step))
              sump <- append(sump, exp(1i*u) + exp(1i*3*u + pi/k)/2)
        ,
         # roteşte punctele cercului 2 cu π/k şi însumează vectorii (∀k)
          for(k in seq(from, to, step))
              sump <- append(sump, exp(1i*u + pi/k) + exp(1i*3*u))  # (?) "/2)"
    )
    return(sump)
}

Din greşeală (şi nu am observat la timp), în scrierea expresiei pentru 'sump' în cazul 2 (rotirea punctelor cercului "mare") am omis să împart la 2 (corect ar fi fost " + exp(1i*3*u) / 2)"; deci în acest caz cele două cercuri au aceeaşi rază, adică se adună vectorial două lanţuri de puncte ale unui aceluiaşi cerc - unul progresând cu raţia unghiulară "u+π/k", iar celălat cu "3u". Până la urmă şi acest nou caz (considerat iată, din întâmplare) s-a dovedit interesant.

Următoarele patru imagini sunt create pe rând, astfel:

u <- seq(0, 2*pi, pi/16)  # prima imagine
plotart(sum_rotate(3, 6, 0.05), tip=2, drv="png")
u <- seq(0, 2*pi, pi/256) # a doua, apoi a treia imagine
plotart(sum_rotate(2, 3, 0.015), tip=2, drv="png")
plotart(sum_rotate(2, 3, 0.02), tip=1, cex=0.4, type="o", col="sienna4", drv="png")
u <- seq(0, 2*pi, pi/32)  # a patra imagine
plotart(sum_rotate(6, 500, 0.2, circle=2), tip=2, col="sienna4", drv="png")

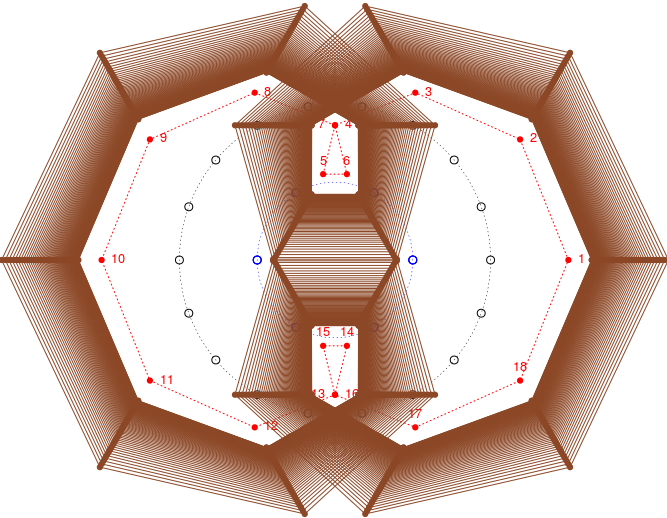
Funcţia sum_rotate() de mai sus se limitează la progresiile "u" şi "3*u"; s-ar fi cuvenit să-i mai prevedem un parametru (cu valoarea implicită 3) - încât să putem viza şi alte cazuri, de exemplu "u" şi "5*u". Ca să nu modificăm nimic în secvenţa de plotări redată mai sus, să înlocuim în corpul acestei funcţii "3*u" prin "5*u"; cu sum_rotate() astfel rescrisă, apelurile plotart() de mai sus ne dau acum imaginile următoare:

Revenind acum la sum_rotate() (poate să adaug parametrul de care ziceam mai sus) - observ o greşeală "de neiertat", care cam face de râs exprimările "roteşte punctele cercului cu π/k", sau "se adună vectorial două lanţuri de puncte ale unui aceluiaşi cerc"; exp(1i*u + pi/k) nu roteşte punctele, ci doar scalează vectorul respectiv cu factorul real e^π/k; abia exp(1i*(u + pi/k)) ar fi asigurat cum intenţionam, rotirea vectorului cu unghiul π/k (iar interpretorul te atenţionează dacă lipseşte o paranteză, dar nu are de ce semnala că lipseşte o pereche de paranteze).

Această greşeală (neintenţionată) a generat totuşi, rezultate interesante. Desigur, în textul de mai sus ar fi de corectat unele formulări, precum aceasta: "rotim cele 10 puncte ale cercului albastru cu π/k (folosind expresia exp(1i*3*u + pi/k)/2), unde k parcurge cu pasul 0.1 intervalul [2.75, 6]"; vectorii de poziţie ai punctelor respective sunt scalaţi (nu rotiţi) şi anume, cu factori din ce în ce mai mici - încât avem şi explicaţia generală a tuturor imaginilor obţinute mai sus: se multiplică un anumit circuit iniţial, repetând construcţia acestuia cu pas din ce în ce mai mic.

Nu reluăm chestiunea, dar ar fi de văzut cum s-ar simplifica şi extinde raţionamentele de mai sus, ţinând seama de faptul că punctele vizate (pe un cerc sau altul, cu un anumit pas unghiular) se pot exprima prin "rădăcinile unităţii", de un anumit ordin.