Adesea, un instrument poate servi şi altor scopuri decât cele pentru care a fost creat…
Cu R se pot manipula şi se pot analiza şi vizualiza sintetic, date statistice (v. r-project.org); dar primitivele grafice, atributele aferente acestora şi funcţiile grafice existente pot fi adaptate şi pe direcţii străine statisticii (v. [1], [2]).

Datele statistice pot fi vizualizate prin puncte (constituind un obiect "scatter-plot"), prin bare dreptunghiulare (ca "histogram"), prin "curbe de densitate" formate din puncte sau din segmente, etc. Mărimea, forma şi culoarea punctelor constituente pot reprezenta diversele caracteristici statistice ale datelor respective şi bineînţeles că au valori adecvate vizualizării unui set de date, care de obicei este foarte numeros.

Dar nu avem vreun obstacol în a folosi dacă dorim, dimensiuni mai mari decât cele obişnuite în grafica statistică - încât "punctul" poate deveni cerc obişnuit, pătrat, triunghi, sau formă grafică de caracter oarecare - şi nici în a repeta cu alţi parametri (pe o aceeaşi lucrare) una sau alta dintre construcţiile grafice posibile. Având astfel câteva figuri geometrice primare şi posibilitatea de a le repeta, se deschide calea către creaţie grafică; dăm mai jos două exemple simple - vizând mai degrabă nu "creaţia grafică" (sau "computer art") ci ansamblul de parametri grafici din R.

Parametrii grafici generali au denumiri prestabilite printr-o listă internă (posibil de accesat prin operatorul ":::") a pachetului de bază graphics:

> graphics:::.Pars  # numele parametrilor grafici generali
 [1] "xlog"      "ylog"      "adj"       "ann"       "ask"       "bg"       
 [7] "bty"       "cex"       "cex.axis"  "cex.lab"   "cex.main"  "cex.sub"  
[13] "cin"       "col"       "col.axis"  "col.lab"   "col.main"  "col.sub"  
[19] "cra"       "crt"       "csi"       "cxy"       "din"       "err"      
[25] "family"    "fg"        "fig"       "fin"       "font"      "font.axis"
[31] "font.lab"  "font.main" "font.sub"  "lab"       "las"       "lend"     
[37] "lheight"   "ljoin"     "lmitre"    "lty"       "lwd"       "mai"      
[43] "mar"       "mex"       "mfcol"     "mfg"       "mfrow"     "mgp"      
[49] "mkh"       "new"       "oma"       "omd"       "omi"       "page"     
[55] "pch"       "pin"       "plt"       "ps"        "pty"       "smo"      
[61] "srt"       "tck"       "tcl"       "usr"       "xaxp"      "xaxs"     
[67] "xaxt"      "xpd"       "yaxp"      "yaxs"      "yaxt"      "ylbias"   

Valorile curente ale acestora pot fi vizualizate şi eventual modificate, prin funcţia par() (şi rămân în vigoare pe parcursul întregii sesiuni de lucru, sau până când sunt din nou modificate în mod explicit). Alţi câţiva parametri grafici (de exemplu, 'asp', pentru "aspect-ratio" y/x) sunt specificaţi în definiţiile unora sau altora dintre funcţiile grafice existente (plot(), axis(), etc.) şi activează de regulă numai pe durata execuţiei funcţiei care i-a setat (sau în contextul trasării graficului curent).

Graficul specific statisticii conţine de regulă patru zone marginale, pentru a reprezenta axele de coordonate şi etichetele corespunzătoare gradaţiilor de pe axe, pentru titluri şi legende; numărul de rânduri alocat acestor zone poate fi gestionat prin parametrul 'mar' (de la "margins"), iar în scopul schiţat mai sus este preferabil să reducem marginile (prima linie din secvenţa de mai jos).

Plotăm nişte puncte, toate de abscisă 0 şi ordonată 0, dar de forme diferite. Prin parametrul 'pch' (de la "point-character") putem stabili forma de reprezentare a punctului; mai jos folosim 'pch = "a"' (alegând "italic", prin specificaţia 'font = 3'), respectiv 'pch = 22', apoi 'pch = 23' şi 'pch = 21' - obţinând ca "punct" în (0, 0) litera "a", respectiv un pătrat, un pătrat rotit cu 90° şi un cerc.

Prin parametrul 'cex' putem scala "punctul" (faţă de o mărime standard predefinită intern), iar prin 'lwd' (de la "line width") putem preciza lăţimea liniilor de trasat; 'col' stabileşte culoarea punctelor sau liniilor, iar 'bg' este "background color". Culoarea poate fi stabilită în multe feluri, între care şi folosind funcţia rgb(); aceasta are ca parametri proporţiile de "Red", "Green" şi "Blue", însoţite eventual de un factor de transparenţă.

opar <- par(mar = c(0, 0, 0, 0))  # anulăm marginile
plot(c(0), c(0), pch = "a", cex = 20, asp = 1, font = 3)
points(c(0), c(0), pch = 22, cex = 42, 
       col = "darkgreen", bg = rgb(0, 1, 0, 0.5))
points(c(0), c(0), pch = 23, cex = 42, 
       col = "blue", bg = rgb(0, 0, 1, 0.3))
points(c(0), c(0), pch = 21, cex = 44,  
       bg = rgb(1, 0, 0.5, 0.4), lwd = 0)
par(opar)  # reconstituie parametrii grafici iniţiali

Am folosit aici patru comenzi: întâi, plot() (care a constituit fereastra grafică şi a "trasat" punctul (0, 0) în forma literei "a"), apoi trei apeluri points() (prin care s-au adăugat pe grafic, pătratele şi cercul). Dar puteam folosi cu acelaşi rezultat, o singură comandă: nu este necesar să plotăm fiecare punct în parte - putem transmite vectorul absciselor şi vectorul ordonatelor punctelor respective, iar pentru parametrii de formă a punctului, de mărime şi culoare putem transmite câte un vector conţinând valorile dorite pentru fiecare punct.

În R nu se lucrează cu valori individuale, ci cu vectori - creaţi cel mai adesea prin funcţia c() (de la "concatenate"). Un "vector" este o secvenţă de una sau mai multe valori care fie au un acelaşi tip (sunt toate de clasă "numeric", sau sunt toate de clasă "character", etc.) fie sunt forţate intern la un acelaşi tip. De exemplu, c('a', 22, 23, 21) - în care avem o valoare de clasă "character" (care este "cel mai mic" tip) şi trei valori numerice - va constitui vectorul de şiruri de caractere ["a", "22", "23", "21"]; în cazul nostru, avem nevoie de valorile numerice - încât vom folosi nu "a", ci codul ASCII corespunzător: c(97, 22, 23, 21).

Alegem un cod ASCII de literă mică oarecare (folosind funcţia sample()), constituim vectorii 'pch', 'cex', 'col' şi 'bg' cu valorile din secvenţa de comenzi redată mai sus (precizăm că rgb(0, 1, 0, 0.5) produce "#00FF0080") şi plotăm punctele respective:

opar <- par(mar = c(0, 0, 0, 0))
x <- rep(0, 4)  # abscisa 0 a patru puncte (de la "repeat")
lit <- sample(97:122, 1) # un cod ASCII de literă mică
p <- c(lit, 22, 23, 21)  # forma punctelor ("pch") 
s <- c(20, 42, 42, 44)  # factori de scalare ("cex")
col <- c("black", "darkgreen", "blue", "white")
bg <- c("white", "#00FF0080", "#0000FF4D", "#FF008066")
plot(x, x, pch=p, cex=s, col=col, bg=bg, asp=1, font=3, lwd=0)
par(opar)

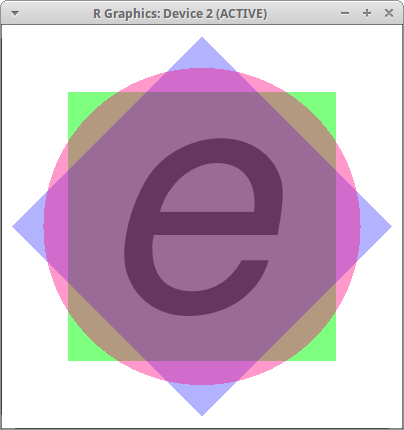
Am zice că figura obţinută este "mai bună" decât prima, fiindcă acum lipseşte conturul şi la pătrate (nu numai la cerc, ca în prima figură); aceasta s-a întâmplat din cauza faptului că am omis să precizăm un vector şi pentru lăţimea liniilor - încât 'lwd=0' specificat în finalul apelului plot() (însemnând "lăţimea 0", sau "fără contur") a fost aplicat fiecărui "punct" De altfel, "întâmplarea" joacă un rol important în "creaţia grafică"…; ar fi de semnalat şi iluzia optică rezultată prin anularea contururilor: cele două pătrate apar uşor curbate spre interior!

Pentru un al doilea exerciţiu de grafică simplă - ne propunem să generăm o tablă de şah.

Funcţia rect() (de la "rectangle") - implicată de funcţia statistică hist() pentru construcţia barelor unei histograme - ne va permite să trasăm pătrăţelele tablei de şah, indicându-i coordonatele a câte două colţuri opuse. Putem constitui coordonatele necesare în diverse moduri; aici, plecăm de la gradaţiile 0, 1, 2, ..., 64 pe fiecare axă şi le vizăm din 8 în 8:

Xi <- 8 * (0:7)  # Xi = [0, 8, 16, 24, 32, 40, 48, 56]
expand.grid(Xi, Xi) -> fields  # coordonatele colţurilor (i, j) unde i,j ∈ Xi
#     str(fields)
#     'data.frame':	64 obs. of  2 variables:
#      $ Var1: num  0 8 16 24 32 40 48 56 0 8 ...
#      $ Var2: num  0 0 0 0 0 0 0 0 8 8 ...
   a    b     c     d     e     f     g     h
1 0,0  8,0  16,0  24,0  32,0  40,0  48,0  56,0
2 0,8  8,8  16,8  24,8  32,8  40,8  48,8  56,8
3 0,16 8,16 16,16 24,16 32,16 40,16 48,16 56,16
4 0,24 8,24 16,24 24,24 32,24 40,24 48,24 56,24
5 0,32 8,32 16,32 24,32 32,32 40,32 48,32 56,32
6 0,40 8,40 16,40 24,40 32,40 40,40 48,40 56,40
7 0,48 8,48 16,48 24,48 32,48 40,48 48,48 56,48
8 0,56 8,56 16,56 24,56 32,56 40,56 48,56 56,56

Aici am redat structura de date obţinută în obiectul "fields" - prin funcţia expand.grid() - chiar în forma şi cu notaţiile de linii şi coloane specifice tablei de şah; pe linia "1" avem coordonatele colţurilor "stânga-jos" ale câmpurilor a1, b1, ..., h1 - ş.a.m.d.; coloana "f" de exemplu, conţine (de sus în jos) coordonatele colţurilor "stânga-jos" ale câmpurilor f1, f2, ..., f8. Vom putea construi câmpul "a1" (de exemplu) prin rect(0, 0, 8, 8), iar câmpul "h8" prin rect(56, 56, 56+8, 56+8).

De data aceasta, să creem imaginea nu pe ecran (ca în cazurile de mai sus), ci într-un fişier ".PNG"; iar pentru culoarea de fundal alegem "transparent", încât ea să nu difere de aceea a paginii în care am insera imaginea respectivă:

png(filename = "tabla_sah.png", bg = "transparent")
opar = par(mar = c(1, 1, 1, 1), mgp = c(3, 0, 0), las = 1, lwd = 0.01, cex = 1.2)

Vom folosi funcţia axis() pentru a nota liniile (la marginea stângă) şi coloanele (dedesubtul tablei) - şi în acest scop am rezervat mai sus prin parametrul "mar", câte un rând pe fiecare dintre cele patru margini; am anulat însă rândul suplimentar prevăzut în mod implicit prin parametrul "mgp", destinat titlurilor adăugate în mod obişnuit pe axe. "las = 1" asigură că notaţia din stânga tablei va fi orientată orizontal (şi nu perpendicular pe axă); am anulat aproape, lăţimea liniei de trasare (dar nu se accepta aici chiar "lwd = 0") - încât borderul pătrăţelelor va fi insesizabil.

Pregătim acum trasarea tablei de şah ("type="n"" asigură că nu se va desena nimic); indicăm limitele 0 şi 64 pentru axe, eliminăm prin "bty="n"" borderul ferestrei grafice şi evităm trasarea axelor (prin "xaxt="n"" şi "yaxt="n""), precum şi etichetarea acestora (prin "xlab=""" şi "ylab="""):

plot(c(0, 64), c(0, 64), asp = 1, type = "n",
     bty = "n", xaxt = "n", yaxt = "n", xlab = "", ylab = "")

În sfârşit, trasăm prin funcţia rect() cele 64 de câmpuri (stabilind culoarea după paritatea sumei dintre indicii de linie şi de coloană), adăugăm notaţiile tablei prin funcţia axis() şi închidem conexiunea cu fişierul (prin funcţia dev.off()):

f1 <- fields[, 1]  # abscisele colţurilor
f2 <- fields[, 2]  # ordonatele acestora
rect(f1, f2, f1 + 8, f2 + 8,  # cele 64 de câmpuri
     col = ifelse((f1/8 + f2/8) %% 2, 
                  "white", "lightgray"))
axis(1, at = seq(4, 60, 8), tick = FALSE, 
     lab = letters[1:8])  # notaţia coloanelor
axis(2, at = seq(4, 60, 8), tick = FALSE, 
     lab = 1:8)  # notaţia liniilor
rect(0, 0, 64, 64, lwd = 1.5, border = "sienna")
dev.off()  # închide fişierul
par(opar)  # reconstituie parametrii iniţiali

Suplimentar (înainte de a închide fişierul), am adăugat tablei de şah un "border" exterior.