Pentru C++ compilatorul analizează şi evaluează expresiile - programatorul nu are acces la funcţiile interne respective. Generarea şi evaluarea de expresii aritmetice folosind C++ necesită modelări prealabile; în [1] am plecat de la un model de arbore binar, nodurile reprezentând operatorii şi operanzii expresiei, cu metode "eval()" şi "print()" corespunzătoare.

Însă în limbajele implementate prin interpretoare, dispunem de regulă de câte o funcţie nativă pentru a evalua direct expresii date ca şiruri de caractere. Iată un exemplu de evaluare directă a unei astfel de expresii - în Python, Perl şi respectiv JavaScript (în mediul Node.js):

vb@Home:~$ python
>>> expr = "6/(1-3/4.)"
>>> eval(expr)
24.0

vb@Home:~$ perl -e '$expr="6/(1-3/4)"; print(eval($expr))'
24 

vb@Home:~$ nodejs
> var expr = "6/(1-3/4)"; eval(expr)
24

În asemenea limbaje, expresiile aritmetice cu patru operanzi se pot obţine direct, fără construcţii prealabile precum în [1]. Vom ilustra lucrurile folosind limbajul R; funcţia parse() analizează sintactic expresia indicată, producând ca rezultat (dacă expresia este corectă) un obiect clasat ca 'expression', reprezentând arborele sintactic al expresiei:

vb@Home:~$ R -q
> expr <- parse(text="6/(1-3/4*)")
## Error in parse(text = "6/(1-3/4*)") : <text>:1:10: unexpected ')'
> expr <- parse(text="6/(1-3/4)")
> expr  ## expression(6/(1-3/4))
> eval(expr)  ## [1] 24

În R se poate lucra şi cu valori infinite, încât nu sunt necesare (spre deosebire de multe alte limbaje) obişnuitele măsuri de evitare a acestora:

> expr <- parse(text="6/(1-(4-3))")
> eval(expr)  ## [1] Inf  (adică 1/0 = infinit)
> expr <- expression(6/(1-4/(2-2)))
> eval(expr)  ## [1] 0  (adică 6/(1-4/0) = - 6/infinit = 0)

Avem 5 tipuri de expresii aritmetice cu 4 operanzi: A(B(CD)) (de exemplu 6*(3/(4+1))), ((AB)C)D (de exemplu ((6*3)/4)+1), (A(BC))D, (AB)(CD) şi A((BC)D). Dacă operanzii sunt distincţi doi câte doi, avem 4! = 24 posibilităţi de a-i întâlni de la stânga spre dreapta în cadrul expresiei; cei trei operatori implicaţi în expresie pot fi aleşi dintre cei patru operatori binari obişnuiţi în 4³ = 64 moduri. Rezultă că avem în total 5×24×64 = 7680 expresii posibile (cu 4 operanzi distincţi, pe un set de 4 operatori binari).

Pentru fiecare triplet de operatori şi pentru fiecare permutare a operanzilor, constituim expresiile de cele cinci tipuri menţionate mai sus alipind corespunzător operanzi, operatori şi paranteze (folosind funcţia paste() pentru alipire şi cat() sau print() pentru afişarea expresiei constituite):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

all4expr <- function(operands=c(1, 3, 4, 6), operators=c('+', '-', '*', '/')) {
    tmp.file <- tempfile()
    sink(tmp.file)
    operands <- combinat::permn(operands)  # lista permutărilor operanzilor
    for(o1 in operators) {
        for(o2 in operators) {
            for(o3 in operators) {
                for(n in operands) {
                    cat(paste0(n[1], o1, '(', n[2], o2, '(', n[3], o3, n[4], ')', ')\n'))
                    cat(paste0('(', '(', n[1], o1, n[2], ')', o2, n[3], ')', o3, n[4], '\n'))
                    cat(paste0('(', n[1], o1, '(', n[2], o2, n[3], ')', ')', o3, n[4], '\n'))
                    cat(paste0('(', n[1], o1, n[2], ')', o2, '(', n[3], o3, n[4], ')\n'))
                    cat(paste0(n[1], o1, '(', '(', n[2], o2, n[3], ')', o3, n[4], ')\n'))
                }
            }
        }
    }
    sink()
    expr <- readLines(tmp.file)
    exdf <- as.data.frame(expr, stringsAsFactors=FALSE)
    exdf$value <- sapply(parse(text=exdf$expr), FUN=eval)
    return(exdf)  # structură de date cu două coloane: 'expr' şi 'value' (pe 7680 linii)
}

Am preferat să generăm întâi toate expresiile într-un fişier temporar şi abia după aceea, să constituim o structură de date de tip "data.frame" în care să întregim coloana expresiilor preluate din fişier cu o coloană corespunzătoare valorilor acestor expresii; apelul sink() în linia 3 şi apoi în linia 18, comută ieşirea programului între ecran şi fişierul temporar constituit în linia 2.

În linia 4 obţinem lista tuturor permutărilor operanzilor, folosindu-ne de funcţia permn() din pachetul combinat (care conţine funcţii utilitare pentru domeniul analizei combinatorice).

În liniile 5, 6 şi 7 generăm tripletele de operatori, folosind cea mai directă metodă - prin trei cicluri imbricate; dar metoda specifică R pentru aceasta, consta în folosirea funcţiei expand.grid():

> expand.grid(rep(list(operators), 3), stringsAsFactors=FALSE)
#   Var1 Var2 Var3
#1     +    +    +
#2     -    +    +
#3     *    +    +
#4     /    +    +
#    ...  ...  ...
#61    +    /    /
#62    -    /    /
#63    *    /    /
#64    /    /    /

Cele 64 de triplete de operatori apar frumos pe linii fiindcă astfel procedează metodele print() asociate implicit diverselor categorii de obiecte; dar de fapt, structura de date rezultată prin expand.grid() este mult mai complicată decât pare şi decât avem nevoie aici, fiind necesare operaţii suplimentare pentru a ajunge la fiecare operator - aşa că am preferat metoda directă (fiind şi ceva mai rapidă).

În sfârşit, pe liniile 19-21 constituim structura de date returnată apoi de funcţie:

> exdf <- all4expr()
> str(exdf)  ## inspectăm structura de date
#'data.frame':	7680 obs. of  2 variables:
# $ expr : chr  "1+(3+(4+6))" "((1+3)+4)+6" "(1+(3+4))+6" "(1+3)+(4+6)" ...
# $ value: num  14 14 14 14 14 14 14 14 14 14 ...
> exdf[sample(nrow(exdf), 3), ]  ## ilustrăm printr-o selecţie aleatorie de 3 linii
#            expr      value
#7250 4/((1/6)+3)   1.263158
#5793 (1/(4+6))+3   3.100000
#4568 (1*(3-6))*4 -12.000000

O singură expresie dintre acestea (cu operanzii 1,3,4,6) are valoarea 24 (a vedea 24_game):

> print(subset(exdf, abs(value-24) < 1e-8))
#            expr value
#6616 6/(1-(3/4))    24

Cu operanzii 1,4,5,6 obţinem exact două expresii de valoare 24:

> exdf <- all4expr(operands=c(1, 4, 5, 6))
> print(subset(exdf, abs(value-24) < 1e-8))
#            expr value
#6716 4/(1-(5/6))    24
#7385 6/((5/4)-1)    24

De menţionat că în principiu am greşi dacă am testa ca pentru numere întregi, cu "value==24" în loc de "abs(value-24) < 1e-8"; de exemplu, pentru 1-5/6 poate rezulta 0.16666666666667, încât în final 4/(1-5/6)=23.9999999999995 (în loc de =24).

Putem ilustra şi cazuri cu operanzi egali, acceptând însă repetarea unei aceleiaşi expresii:

> print(subset(all4expr(operands=c(3, 8, 3, 8)), abs(value-24) < 1e-8))
#            expr value
#6616 8/(3-(8/3))    24  ## o singură expresie, repetată apoi de 3 ori 
#6661 8/(3-(8/3))    24
#6686 8/(3-(8/3))    24
#6711 8/(3-(8/3))    24

Pentru operanzii 4,5,6,9 găsim exact 120 de expresii de valoare 24 - dar toate derivă din 4+5+6+9 = 24 (permutând operanzii şi angajând parantezele în cele 5 moduri posibile). Pentru operanzii 2,5,8,9 - care iarăşi însumează 24 - pe lângă cele 120 expresii folosind numai '+', avem încă un număr de alte expresii de valoare 24, de exemplu ((8-5)+9)*2.

Nicio expresie (cu operatori dintre cei patru operatori aritmetici standard) cu operanzii 1,6,7,8 sau cu operanzii 3,4,6,7 nu are ca valoare 24 (şi numai acestea două sunt cazurile de expresii fără valoarea 24, pentru operanzi distincţi aleşi dintre cifrele zecimale 1..9).

Dar nimic din cadrul funcţiei redate mai sus nu obligă operanzii să fie de câte o singură cifră, sau operatorii să fie numai dintre cei patru operatori aritmetici standard. De exemplu, apelând funcţia de mai sus pentru operanzii 1, 5, 11, 13 nu obţinem nicio expresie de valoare 24; dar adăugând şi operatorul '^' pentru "ridicare la putere":

> print(subset(all4expr(operands=c(1,5,11,13), operators=c('+','-','*','/','^')), 
               abs(value-24) < 1e-8))

găsim şi expresii de valoare 24, banale (speculând că 1ⁿ=n) precum 11+(13*(1^5)), dar şi una chiar frumoasă: (5^(13-11))-1 (adică 5^13-11-1 = 24).

Putem analiza seturi de date constituite ca mai sus, la fel cum facem cu seturile de date uzuale. Ne-ar putea interesa repartiţia valorilor expresiilor aritmetice respective:

> exdf <- all4expr(operands=c(1,3,4,6))  # sau un alt set de operanzi
> exdf1 <- subset(exdf, value != Inf)  # excludem valorile infinite
> summary(exdf1)
#     expr               value        
# Length:7668        Min.   :-71.000  
# Class :character   1st Qu.:  0.000  
# Mode  :character   Median :  3.042  
#                    Mean   :  7.863  
#                    3rd Qu.:  9.000  
#                    Max.   : 96.000  

Vedem astfel că valorile expresiilor aritmetice peste operanzii 1,3,4,6 sunt cuprinse între -71 şi 96 (am exclus expresiile de valoare infinită), având 7.863 ca medie; 25% dintre aceste valori sunt negative, 50% dintre ele sunt între 0 şi 9, iar restul de 25% sunt peste 9.

Ne-ar putea interesa frecvenţa valorilor luate de expresiile respective:

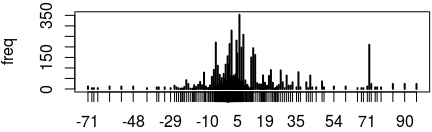
> freq <- table(exdf1$value)  # frecvenţa valorilor
> str(freq)
# 'table' int [1:380(1d)] 12 4 4 4 12 12 12 4 8 8 ...
# - attr(*, "dimnames")=List of 1
#  ..$ : chr [1:380] "-71" "-69" "-68" "-66" ...
> plot(freq)  # histograma alăturată

Cele 7668 de expresii din "exdf1" au în total 380 de valori (şi citim din ceea ce s-a afişat mai sus că 12 expresii au valoarea -71, alte 4 expresii au valoarea -69, etc.). Ghidându-ne după histograma redată mai sus şi eventual listând tabelul "freq", putem constata că 353 de expresii au valoarea 6, iar acesta este numărul maxim de expresii cu o aceeaşi valoare; 70 de expresii au valoarea 4, 230 de expresii au valoarea 4.5, 150 de expresii au valoarea 12, etc.

Un anumit farmec ar avea valorile care pot fi exprimate numai într-un singur fel, prin operanzii şi operatorii respectivi:

> freq1 <- freq[freq==1]
> str(freq1)
# 'table' int [1:48(1d)] 1 1 1 1 1 1 1 1 1 1 ...
# - attr(*, "dimnames")=List of 1
#  ..$ : chr [1:48] "-24" "-18" "-6.5" "-5.5" ...

În cazul nostru (pentru operanzii 1,3,4,6) avem 48 de valori care sunt exprimate prin câte o singură expresie (folosind cei patru operatori standard): -24, -18, -6.5, etc. Desigur că vrem să vedem şi expresiile corespunzătoare acestor 48 de valori:

> expr.solo <- subset(exdf1, value %in% dimnames(freq1)[[1]])
> expr.solo[order(expr.solo$value), ]  # cele 48 de expresii, ordonate după valoare
#            expr        value
#7420 6/((3/4)-1) -24.00000000
#6621 6/(1-(4/3)) -18.00000000
#3482 ((1-3)/4)-6  -6.50000000
## ... ... ...
#6701 6/(3-(1/4))   2.18181818
#6616 6/(1-(3/4))  24.00000000

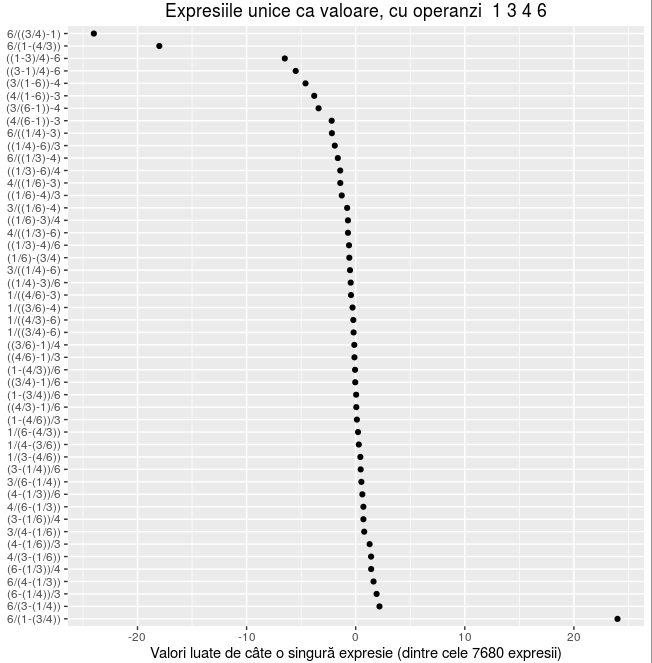
Am putea reda cele 48 de expresii şi prin graficul următor (necesitând pachetul ggplot2):

ggplot(expr.solo, aes(reorder(expr, -value), value)) + geom_point() +
    labs(x="", y="Valori luate de câte o singură expresie (dintre cele 7680 expresii)", 
         title="Expresiile unice ca valoare, cu operanzi 1,3,4,6") +
    coord_flip()

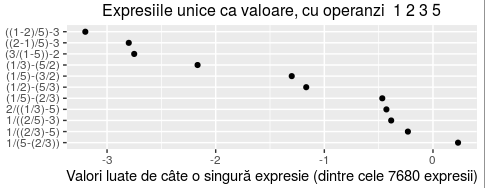
Pentru setul de operanzi 1,2,3,5 - reluând comenzile de mai sus - găsim numai 11 valori (între -3.2 şi 1/(5-(2/3))=3/13) care sunt exprimate prin câte o singură expresie (construită cu operanzii respectivi şi cu trei dintre cei patru operatori aritmetici standard):

În partea a II-a vom folosi funcţia all4expr() şi vom îmbina comenzile de mai sus pentru a încerca să evidenţiem diverse caracteristici privind unicitatea expresiilor care au anumite valori, considerând toate cele 126×7680 expresii aritmetice posibile pentru patru operanzi dictincţi aleşi dintre cele 9 cifre zecimale nenule, cu trei operatori dintre cei patru operatori binari standard.