Expresii aritmetice în R (partea a II-a)
Avem 126 de seturi de câte 4 operanzi distincţi, aleşi din mulţimea {1, 2, ..., 9}:
Seturile respective se pot obţine folosind funcţia combn() din pachetul "utils"- de exemplu:
> combn(5, 4) # cele 5 combinări de 5 elemente luate câte 4 (apar pe coloane) # [,1] [,2] [,3] [,4] [,5] # [1,] 1 1 1 1 2 # [2,] 2 2 2 3 3 # [3,] 3 3 4 4 4 # [4,] 4 5 5 5 5
Prin argumentul opţional 'FUN' se poate specifica o funcţie care urmează să se aplice fiecărei combinări, sau fiecărui element al acesteia; de exemplu, să ridicăm la pătrat:
În mod implicit, combn() returnează o matrice - combinările fiind înscrise pe coloane; cu funcţia t() putem transpune matricea respectivă. Pentru a returna o listă în loc de matrice, combn() trebuie apelat setându-i parametrul opţional 'simplify'=FALSE.
Pentru unul oarecare dintre aceste seturi, funcţia all4expr() din [1] construieşte o structură de date "exdf" de tip 'data frame' conţinând toate expresiile aritmetice posibile cu operanzii respectivi şi cu trei (distincţi sau nu) dintre cei patru operatori binari elementari:
Ne interesează (încă din [1]) valorile care sunt exprimate prin câte una singură dintre cele 7680 de expresii posibile cu operanzii respectivi; aceste valori definesc o restricţie injectivă a funcţiei de evaluare ev(expresie)=valoare şi desigur, ne interesează şi expresiile implicate - pe care le numim "expresii injective" (faţă de setul de operanzi respectiv).
Vizualizarea expresiilor injective cu animare după operanzi
Pe argumentul 'FUN' al funcţiei combn() montăm o funcţie anonimă care pentru combinarea curentă apelează all4expr(), determină frecvenţa fiecăreia dintre valorile expresiilor obţinute astfel, selectează liniile de date corespunzătoare valorilor de frecvenţă 1 şi plotează apoi, valorile respective:
Prin secvenţa de comenzi redată mai sus vizualizăm rând pe rând (cu funcţii din pachetul ggplot2) cele 126 de subseturi de expresii (cu patru operanzi 1..9 distincţi) care corespund valorilor de frecvenţă 1; ilustrăm aici pentru cazul mai scurt al operanzilor 1..6:
În loc de vizualizarea (chiar dacă şi animată…) indicată şi exemplificată mai sus, probabil că - în scopul investigării ulterioare - ar fi preferabil să constituim o structură "data frame" conţinând expresiile şi valorile care ne interesează. La prima vedere, ar fi simplu: înlocuim liniile pe care este formulată mai sus vizualizarea (prin 'ggplot()') cu secvenţa de comenzi care să încastreze succesiv expresiile respective într-o structură 'data frame' preexistentă.
Fişier text cu expresiile valorilor unice
Este poate, aşa de simplu cum ne aşteptăm - dacă preferăm să înscriem datele respective într-un fişier text (în loc de a le structura în memorie):
Chiar dacă apelul funcţiei combn() se încheie acum cu un mesaj de "eroare" ("dims [product 3780] do not match the length of object [252]") - rezultă fişierul aşteptat:
expr value
((1-2)/4)-3 -3.2500000
((2-1)/4)-3 -2.7500000
((1/2)-4)/3 -1.1666667
... ...
2/((1/3)-4) -0.5454545
expr value
((1-2)/5)-3 -3.2000000
((2-1)/5)-3 -2.8000000
... ...
Fişierul conţine 8849 de linii şi dacă scădem cele 126 linii de "antet" conţinând cele două denumiri de coloane pentru fiecare set de operanzi - rezultă că în cauză sunt 8723 de expresii, adică exact cât vom regăsi altfel mai jos (deci am putea ignora mesajul de "eroare" afişat în final).
De fapt, liniile respective au fost produse prin execuţia comenzii print(expr.solo) din corpul funcţiei redate mai sus, pentru fiecare dintre cele 126 de combinări, rând pe rând; dacă întrerupem execuţia secvenţei de mai sus (cu tastele CTRL + C) după să zicem 30 de secunde de la momentul lansării ei, atunci vom constata că fişierul "solo129.txt" prevăzut la început conţine deja aproape jumătate dintre cele 8849 linii - confirmând că se scrie efectiv în fişier pentru fiecare combinare în parte (desigur, în cazul întreruperii execuţiei, comanda sink() din finalul secvenţei trebuie re-tastată - altfel, ieşirile vor fi în continuare dirijate spre fişierul menţionat).
Însă combn() are de returnat - nu de afişat - matricea (sau lista) conţinând combinările respective: se iniţializează un obiect 'matrix' sau unul 'list' - în funcţie de valoarea 'TRUE' sau 'FALSE' a argumentului 'simplify' - şi apoi se generează rând pe rând câte o combinare dintre cele 126 posibile şi i se aplică funcţia din argumentul 'FUN', înscriind rezultatul curent pe coloana curentă din matrice (respectiv, pe locul curent din listă); în final, se returnează matricea sau lista astfel constituită.
Am putut constata că într-adevăr aşa procedează combn(), filând codul sursă: tastând numele funcţiei (fără paranteze), interpretorul R afişează codul sursă al funcţiei (aceasta fiind scrisă în R).
În R, dacă rezultatul produs de apelul unei funcţii nu este atribuit explicit unei anumite variabile - atunci el este "atribuit" automat ca ieşire pe ecran (sau pe fişierul setat prin funcţia sink()). Prin urmare, secvenţa de mai sus ar trebui să adauge în fişier - după cele 8849 linii scrise explicit - şi matricea sau lista rezultatelor constituite intern de combn(); nu a reuşit să le adauge, încheind cu mesajul de eroare evocat mai sus - dar dacă apelăm prin combn(9, 4, simplify=FALSE, FUN=...) atunci se adaugă în fişier şi lista cu 126 de componente (fiecare fiind de tip 'data frame') constituită intern de către combn() - rezultând de două ori aceleaşi 8723 expresii şi valori (şi chiar cu o suplimentare mai degrabă inutilă şi chiar supărătoare de informaţii - nume de linii, indecşi, etc.).
Cu aceste precizări şi lămuriri, devine clar că secvenţa de mai sus - bazată pe sink() şi apoi, pe print() interior funcţiei montate pe argumentul 'FUN' - este principial greşită, neţinând cont de modul în care fiinţează funcţiile în limbajul R (dar… a înţelege lucrurile şi a le corela, sau "a învăţa pe propria piele" este o experienţă întreagă, superioară învăţării regulilor din vreun manual de utilizare).
Putem simplifica acum secvenţa incriminată mai sus (eliminând efectele secundare):
Rezultă o listă în care fiecare dintre cele 126 de componente este un obiect de tip 'data frame', conţinând variabilele 'expr' şi 'value' corespunzătoare expresiilor valorilor unice pentru câte una dintre cele 126 de combinări (ale operanzilor 1..9 luaţi câte 4):
> str(cb9) #List of 126 # $ :'data.frame': 15 obs. of 2 variables: # ..$ expr : chr [1:15] "((1-2)/4)-3" "((2-1)/4)-3" "((1/2)-4)/3" "((1/4)-2)/3" ... # ..$ value: num [1:15] -3.25 -2.75 -1.167 -0.583 -1.375 ... # $ :'data.frame': 11 obs. of 2 variables: # ..$ expr : chr [1:11] "((1-2)/5)-3" "((2-1)/5)-3" "(3/(1-5))-2" "(1/2)-(5/3)" ... # ..$ value: num [1:11] -3.2 -2.8 -2.75 -1.167 0.231 ... ### ... ###
Acum putem înscrie într-un fişier text cele 126 de seturi de expresii astfel:
obţinând cele 8849 de linii de date descrise la început. Dar mai mult - folosind secvenţa:
putem re-obţine "vizualizarea animată a expresiilor injective" (a vedea primul program - care deasemenea este "principial greşit", fiindcă angaja şi el "efecte secundare").
Am putea transforma structura de date 'cb9' într-una mai convenabilă, folosind unsplit(cb9, factor): cele 126 de componente de tip 'data.frame' (de câte două coloane) ale obiectului de tip 'List' care este cb9, vor fi combinate într-o singură structură 'data.frame', având rândurile în ordinea dată de 'factor'. Este firesc să grupăm rândurile după operanzii implicaţi în expresiile de pe acele rânduri şi putem folosi funcţia gsub() pentru a obţine etichetele necesare:
Însă a proceda astfel pentru a constitui factorul respectiv este cum nu se poate mai ineficient (fiind de apelat gsub() pentru mai mult de 7000 de expresii şi mai trebuind să rezolvăm şi situaţia evidenţiată în exemplul de mai sus, când expresii cu aceiaşi operanzi capătă etichete distincte).
Structurarea în memorie a expresiilor injective
Având datele în format text este foarte bine - putem folosi diverse limbaje şi programe utilitare pentru a le investiga şi în particular, în R dispunem de comenzi pentru a prelua datele din fişierul respectiv şi a le constitui în diverse structuri de memorie. Totuşi, vrem să le constituim direct într-o structură 'data frame', fără înscrierea intermediară într-un fişier text a datelor respective (dar şi fără intermedierea listei de 126 obiecte 'data frame' obţinute mai sus, "cb9").
Dar pentru aceasta, oarecum surprinzător - lucrurile n-au mai fost aşa de simple cum ne păreau; până la urmă, am folosit pachetul dplyr (prin funcţia dplyr::union() am putut "alipi" succesiv obiectele 'data frame' aferente celor 126 de seturi de expresii) şi am folosit funcţia 'combinat::combn()' (în locul celei standard utils::combn() pe care o angajasem în programele precedente):
În linia a doua se instituie un obiect "solo" (iniţial vid de date), în care urmează să fie înscrise datele care ne interesează; am prevăzut cele două coloane 'expr' şi 'value' existente în obiectul 'exdf' din care se vor prelua expresiile şi valorile, dar şi o a treia coloană 'operands' - pentru a păstra ca şir de caractere operanzii indicaţi de combinarea curentă (ulterior, după ce vom fi obţinut rezultatul dorit, vom converti variabila solo$operands în 'factor' având ca nivele cele 126 de combinări).
Funcţia anonimă montată pe argumentul 'fun' (nu 'FUN', cum era în cazul utils::combn()) are acces numai la variabilele din contextul intern al funcţiei combinat::combn() (fiind apelată din interiorul acesteia) şi pentru a viza variabila "globală" 'solo' (care este situată în afara mediului combn()) am folosit operatorul de atribuire "<<-" (a vedea ultima linie din secvenţa de comenzi redată mai sus) şi nu pe cel obişnuit "<-"; cu solo <- union(solo, expr.sol) s-ar fi creat o variabilă "locală" 'solo', în care se vor fi îmbinat pas cu pas cele 126 de subseturi de expresii - dar rezultatul final s-ar fi pierdut odată cu încheierea execuţiai funcţiei combn() (obiectul "global" solo' rămânea vid).
Putem fi în câştig, dacă ne lovim din când în când de fel de fel de subtilităţi…; dar în cazul de faţă le puteam ocoli, renunţând să folosim maniera funcţională în care este specificată funcţia combn() şi folosind în schimb o instrucţiune repetitivă "for":
Timpul de execuţie pentru această ultimă variantă este totuşi ceva mai mare (cu vreo 10-15 secunde) faţă de varianta (cu anumite "subtilităţi" de natură funcţională) precedentă.
În structura de date obţinută cu una sau alta dintre aceste variante de program, convertim variabila 'operands' la tipul "factor" (şi inspectăm rezultatul final):
Liniile de date corespunzătoare unui aceluiaşi nivel al factorului 'operands' reprezintă expresiile injective pentru operanzii respectivi; dar unele dintre valorile acestora se pot întâlni şi la expresiile injective ale vreunui alt set de operanzi. Apar în mod firesc sau ne putem pune diverse probleme, privitoare la repartiţia valorilor celor 8723 de expresii; de exemplu: care valori au preimagini unice în mulţimea celor 8723 de expresii?
Deocamdată, putem găsim caracteristicile de bază folosind funcţia summary():
Avem 8723 linii de date (expresii), dintre care 130 (cel mai multe) corespund operanzilor etichetaţi prin 4679; cu alte cuvinte - numărul maxim posibil de expresii aritmetice elementare cu aceiaşi patru operanzi 1..9 care sunt preimagini unice de valori ale expresiilor respective este 130 şi este atins pentru operanzii 4,6,7,9 (oare… chiar aşa este - sunt exact 130?).
Valorile celor 8723 de expresii sunt cuprinse între -72 şi 63, iar 50% dintre ele se încadrează în intervalul [-2.2, 0.4792] (definit de prima şi a treia quartilă).
Să vedem câte linii de date corespund fiecăreia dintre cele 126 categorii de operanzi:
Vedem de exemplu, că pentru operanzii etichetaţi de 1235 avem numărul minim posibil de exprimări unice în privinţa valorii; este greu de sugerat vreo regulă, dar vedem că pentru operanzi mici 1..5, avem "puţine" expresii de valori unice (11, apoi 15, 26, ş.a.m.d.), iar pentru operanzi mari 5..9 avem "multe" (121 pentru setul 5678, 122 pentru 4789, etc.).
Fiindcă vrem totuşi o imagine grafică pentru frecvenţa valorilor unice pe categoriile de operanzi, să convertim tabelul obţinut mai sus într-o structură 'data frame' (cum aşteaptă funcţia ggplot()):
> as.data.frame(op.freq) -> op.freq.df > head(op.freq.df, 3) # Var1 Freq #1 1235 11 #2 1234 15 #3 1236 26
Fiindcă tabelul op.freq fusese ordonat după frecvenţe (în urma folosirii mai sus, a funcţiei sort()) - liniile structurii op.freq.df rezultate mai sus rămân ordonate crescător după frecvenţă. Următoarea secvenţă de comenzi construieşte câte o bară verticală pentru fiecare dintre cele 126 de seturi de operanzi, de înălţime egală cu numărul de expresii peste acel set de operanzi, barele succedându-se de la stânga spre dreapta în ordinea crescătoare a înălţimilor:
ggplot(op.freq.df, aes(x=Var1, y=Freq)) + geom_bar(stat='identity', colour="#eeeeee", fill="#dd8888") + theme(axis.text.x = element_text(angle=90, hjust=0.5, vjust=0.5, color="#660000", size=7)) + geom_hline(yintercept=seq(10, 130, by=10), colour="white", linetype="dashed")
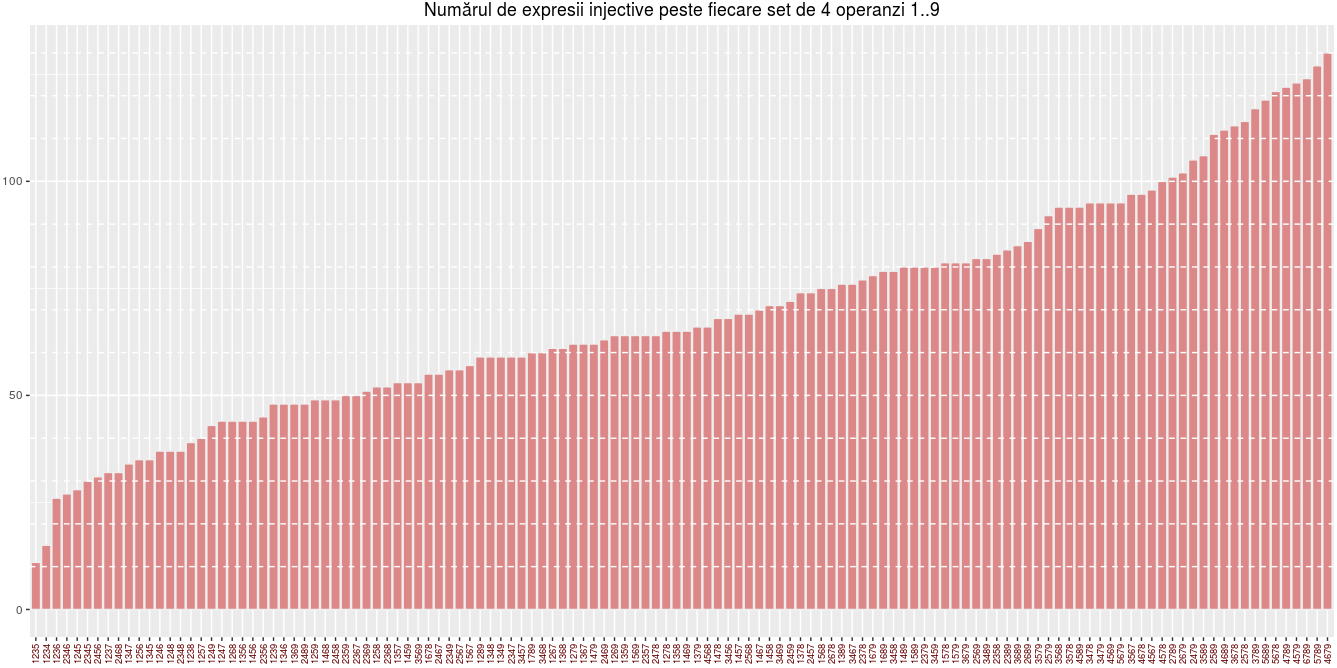
Imaginea redată poate fi mărită (click-dreapta, "View Image"), pentru a vedea că barele au fost etichetate prin operanzii corespunzători, etichetele respective fiind plasate vertical şi exact dedesubtul fiecărei bare (folosind funcţia ggplot2::theme() şi alegând adecvat parametrii 'angle', 'hjust' şi 'vjust' în funcţia element_text(), în cadrul secvenţei de mai sus).
oare…
Dar iată şi o altă problemă: OARE aşa este - avem exact 15 expresii injective peste operanzii
'1234', 11 peste '1235', 48 expresii injective peste operanzii '1346'…? Îndoiala apare dacă ne gândim că valorile expresiilor respective nu sunt neapărat numere întregi, iar operaţiile în "virgulă mobilă" pot produce surprize şi nu-i rău să mai şi verificăm din când în când.
Apelăm din [1] all4expr(), obţinând în 'tst.ex' cele 7680 de expresii cu operanzii 1,3,4,6. Pentru ca ulterior să putem repera uşor expresiile, ordonăm după valorile expresiilor şi resetăm numele de rânduri (căci ordonarea conservă numele). Apoi, marcăm valorile de frecvenţă 1 - cel puţin, aşa le găseşte funcţia pe care o folosim aici table() - şi extragem liniile respective în 'tst.ex.inj':
Inspectând în paralel cele două seturi de date, constatăm că expresia ((4/3)-1)/6 apare în 'tst.ex.inj':
> options(digits=15) # pentru a afişa cu 15-16 cifre zecimale > tst.ex.inj # conţine 48 de linii de date ("expresii injective") # expr value ## ... #2037 (1-(3/4))/6 0.0416666666666667 #2044 ((4/3)-1)/6 0.0555555555555555 # pe linia 2044 din 'tst.ex' ## ... #6742 6/(1-(3/4)) 24.0000000000000000
> tst.ex[2040:2050, ] # inspectăm în jurul liniei 2044 expr value #2040 ... #2044 ((4/3)-1)/6 0.0555555555555555 # = 1/18 #2045 1/(6+(3*4)) 0.0555555555555556 # = 1/18 #2046 1/(6+(4*3)) 0.0555555555555556 # = 1/18 #2047 ...
De fapt, ((4/3)-1)/6 = 0.(3)/6 = 1/18, iar expresiile de pe liniile 2045-2048 au şi ele, valoarea 1/18; prin urmare, această expresie nu trebuia inclusă între expresiile injective. Rezultă că numărul de expresii injective peste operanzii '1346' este 47 (şi nu 48, cât găsisem iniţial).
Probabil că şi pentru alte seturi de operanzi va trebui să scădem - dar probabil, cu foarte puţin - numărul de expresii injective, faţă de ce găsisem mai sus. Important sau nu (mai degrabă nu), s-ar pune totuşi - poate într-o a III-a parte - problema determinării exacte (dar într-un mod cât mai simplu şi imediat) a frecvenţei valorilor unui set de expresii aritmetice.
vezi Cărţile mele (de programare)