5. Obţinerea preimaginilor originii

Pentru orice punct $z \ne 0$ putem determina $z_1=N(z)=z-\dfrac{z^n-1}{nz^{n-1}}=\dfrac{(n-1)z^n+1}{nz^{n-1}}$; dacă $z_1\ne 0$, putem obţine $z_2=N(z_1)=N(N(z))=N^{\circ 2}(z)$ şi dacă $z_2 \ne 0$ - putem continua "orbita" lui $z$ cu $z_3=N(z_2)=N^{\circ 3}(z)$, ş.a.m.d. Dacă la un anumit moment $z_k=N^{\circ k}(z)=0$, atunci iterarea nu mai trebuie continuată (am avea "împărţire la zero", deci $z_{k+1}=\infty$); în acest caz $z$ este punct "de excepţie" (nu orbitează spre vreuna dintre rădăcinile unităţii; v. [1]).

Deci preimaginile lui $0$ formează o submulţime - strictă, cum vom arăta mai târziu în §6 - a mulţimii tuturor punctelor "de excepţie". Avem $n$ preimagini "imediate" ale lui $0$ - anume, punctele $z$ pentru care $(n-1)z^n=-1$; fiecare dintre acestea are câte $n$ preimagini, deci avem (cel puţin) $n^2$ preimagini "de odinul doi" ale lui $0$, ş.a.m.d.

Dacă $\zeta$ este o preimagine de un anumit ordin a lui $0$, pentru a găsi preimaginile lui $\zeta$ avem de rezolvat ecuaţia $N(z)=\zeta \iff (n-1)z^n-n\zeta z^{n-1}+1=0$; următoarea funcţie produce o funcţie care, primind parametrul $\zeta$ returnează vectorul celor $n$ coeficienţi ai polinomului din această ecuaţie (în ordinea crescătoare a gradelor monoamelor):

poly_newton <- function(n) {
  function(zeta) c(1, rep(0, n-2), -n*zeta, n-1)
}

Putem obţine rădăcinile unui polinom folosind funcţia polyroot(); de exemplu, pentru $n=4$ avem $N(z)=0 \iff 3z^4=-1 \iff z=3^{-1/4}\sqrt[4]{-1}=3^{-1/4} {\boldsymbol e}^{{\boldsymbol {i(2h\pi + \pi)/4}}}{\textstyle ,~\small h=0..3}$ - ceea ce verificăm acum şi astfel:

pn4 <- poly_newton(4)
print(polyroot(pn4(0)))  # rădăcinile ecuaţiei 3z^4 + 1 = 0
[1]  0.537285+0.537285i -0.537285+0.537285i -0.537285-0.537285i  0.537285-0.537285i
print(3^(-1/4)*exp(1i*(2*(0:3)+1)*pi/4))  # (atestând rădăcinile obţinute mai sus)

Dacă vectorul 'roots' conţine preimaginile lui $0$ (de un acelaşi anumit ordin), atunci putem folosi mecanismul apply() pentru a obţine mulţimea tuturor preimaginilor acestora:

sapply(roots, function(r) polyroot(pn4(r)))  # rezolvă N(z)=r pentru ∀r ∈ 'roots'

În final, putem asambla cu cele de mai sus următoarea funcţie, prin care obţinem mulţimea preimaginilor lui $0$ până la o anumită adâncime de iterare:

orb2zero <- function(n = 3, iterations = 10) {
  poly_newton <- function(deg) {
    function(zeta) c(1, rep(0, deg-2), -zeta*deg, deg-1)
  }
  pn <- poly_newton(n)
  get_preimages <- function(roots) {
    as.vector(sapply(roots, function(r) polyroot(pn(r))))
  }
  allr <- roots <- polyroot(pn(0))
  for(i in 1:iterations) {
    roots <- get_preimages(roots) 
    allr <- append(allr, roots)  # append(allr, roots[abs(roots) < 1.56])
  }
  return(allr)
}

Nu ne speriem deocamdată de faptul că este necesară multă memorie şi în plus, execuţia poate dura mult (pentru $n \gt 4$, sau/şi 'iterations' > 10); vom vedea poate mai târziu, cum s-ar formula mai eficient funcţia de mai sus. O idee de reducere (eventual, chiar "drastică") a cerinţei de memorie este deja sugerată în linia de comentariu din textul funcţiei redat mai sus: păstrăm numai preimaginile care se află într-un anumit disc (de rază 1, de exemplu) centrat în origine.

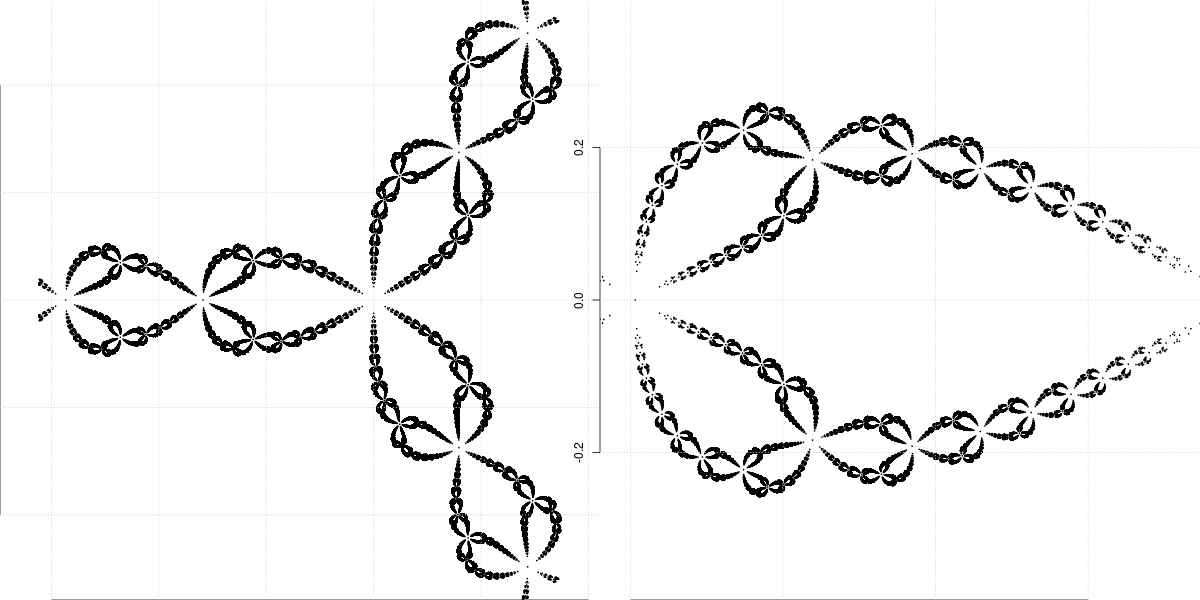
Putem folosi orb2zero() (pentru a obţine imagini precum cele tocmai redate), după modelul:

orb <- orb2zero(it=12)
orb <- orb[abs(orb) < 1.56]  # restrânge la un anumit disc centrat în origine
png <- png("orb2zero.png", units="px", width=1200, height=600, bg="white")
opar <- par(mfrow = c(1, 2), mar=c(0, 0, 0, 0), bty="n")
plot(orb, pch=20, cex=0.01, asp=1); grid()  
orb <- orb[Re(orb) < -0.05 & Re(orb) > -2^(-1/3)-0.05]  # selectează o "petală"
plot(orb, pch=20, cex=0.01, asp=1); grid()
dev.off(); par(opar)

După ce am obţinut în vectorul 'orb' preimaginile lui $0$ (până la ordinul 12), am selectat numai pe cele aflate într-un anumit disc centrat în origine (experimentând cu diverse raze) şi respectiv (pentru a doua imagine), pe cele corespunzătoare unui anumit detaliu (aici, "petala" formată în stânga originii) - şi am plotat apoi punctele respective.

Imaginile rezultate "trunchiază" mulţimea denumită de obicei mulţimea Julia a transformării respective; aceasta este frontiera comună a bazinelor de atracţie ale rădăcinilor polinomului, pe întregul plan (în vecinătatea oricât de mică a oricărui punct al ei există "pre-imagini" ale fiecărei rădăcini - cu interpretarea şocantă că în fiecare punct "se întâlnesc" câte $n$ culori; "pre-imagine" a rădăcinii însemnând aici un punct a cărui orbită converge la o rădăcină a polinomului).

Dacă ignorăm contextul şi vedem imaginile ca atare, ne-am putea gândi să testăm anumite transformări asupra vectorilor 'orb' din secvenţa de mai sus; de exemplu, plotând pătratele acestora (plot(orb^2, ...)) găsim:

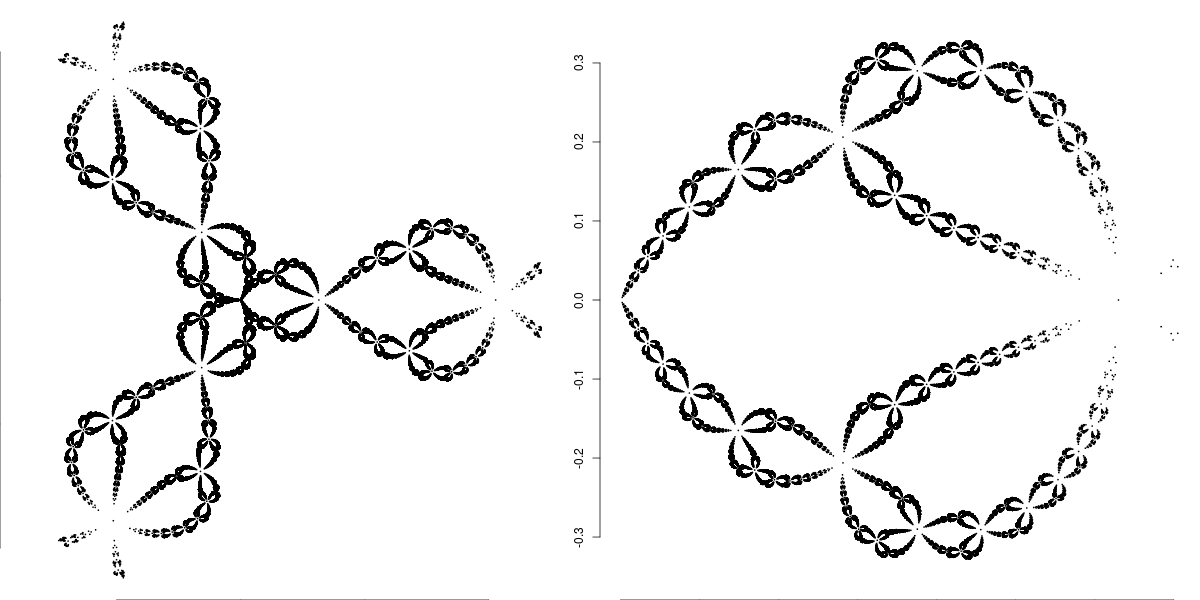
Este discutabil dacă asemenea transformări au vreo relevanţă pentru fractali, dar vedem că pot rezulta şi "decoraţiuni" interesante.

Rămânând la terminologia modestă din [1], ne propunem în §6 să căutăm şi altfel de "puncte de excepţie" (cele ale căror orbite sunt şiruri periodice neatractoare).