Exceptând anumite puncte iniţiale, şirul $z, N_g(z), N_g(N_g(z)), ...$ cu $N_g(z)=z - g(z) / g'(z)$ ("metoda lui Newton"), orbitează spre unul dintre zerourile funcţiei derivabile $g()$. Ca şi în [1], considerăm polinomul $g(z)=z^n-1$, care are ca zerouri rădăcinile de ordinul n ale unităţii.

1. O primă impresie asupra punctelor "de excepţie"

În [1] am sesizat într-un anumit experiment că pentru n = 4, punctele y = ±x exceptează de la regula menţionată: acestea orbitează oscilatoriu pe bisectoarea respectivă (fără să devieze spre o rădăcină). Am încercat să reliefez cumva asemenea puncte "de excepţie", simplificând doar, programul din [1] (fără "teorie" suplimentară); rezultatele - mai mult sau mai puţin credibile - depind de numărul maxim de iteraţii, de eroarea cu care determinăm limitele şi de "densitatea" punctelor indicate:

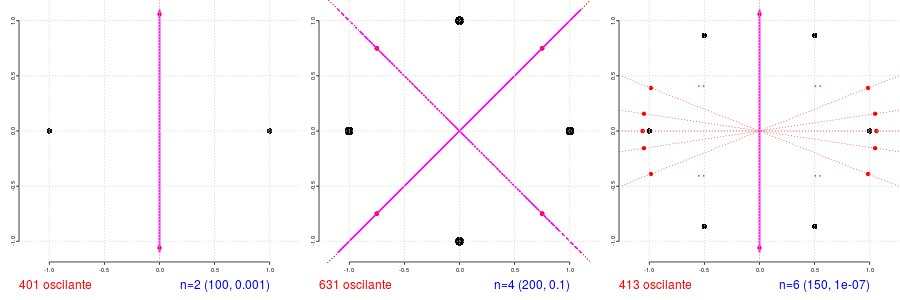
Punctele negre reprezintă atractorii (rădăcinile unităţii); punctele roşii sintetizează puncte "de excepţie" găsite (în limita numărului de iteraţii) pe o aceeaşi direcţie (punctată cu roşu, uneori acoperit cu magenta); în a treia imagine (pentru n = 6) se pot distinge nişte puncte izolate (câte două în fiecare cadran), colorate cu magenta - ele diferă de cele roşii prin faptul că pe direcţia care corespunde fiecăruia nu s-au găsit (în domeniul considerat) alte puncte "de excepţie".

Nu am reprezentat înseşi rădăcinile unităţii, ci chiar "atractorii" rezultaţi prin procesul iterativ - aşa că "mărimea" unui punct negru spune ceva despre valoarea EPS folosită. În al doilea caz avem EPS = 0.1, însemnând că iterarea se încheie într-un punct distanţat cu cel mult 0.1 faţă de rădăcina atractoare; rezultă astfel mai multe puncte negre, "înghesuite" în vecinătatea de rază 0.1 a atractorului propriu-zis - încât avem impresia unui punct negru "mai mare".

În al treilea caz, punctele roşii (şi cele magenta) exterioare axei verticale dispar, dacă mărim numărul de iteraţii (de la 150 la 200) - ceea ce interpretăm desigur ca "succes": şi ele orbitează (chiar dacă pe o lungime mai mare) spre una dintre rădăcinile atractoare…

Să remarcăm mesajul informativ "401 oscilante"; în program aveam x = seq(-1.1, 1.1, length=401) - încât într-adevăr, avem exact 401 ordonate (şi tot atâtea, abscise de puncte). În schimb, "631 oscilante" din al doilea caz pare greşit: având 401 × 401 puncte (echidistanţate pe orizontală şi pe verticală, cum subînţelege funcţia seq()) - ar trebui să rezulte 2*401 puncte "diagonale" (şi nu doar 631); aceasta poate însemna că nu toate punctele diagonalelor sunt "de excepţie", dar ar putea fi vorba şi de o anumită deficienţă (inerentă) de calcul numeric…

seq(a, b, length = k) furnizează o secvenţă de k puncte "echidistanţate" între capetele a şi b, fiecare subinterval având lungimea (b - a) / (k - 1) - dar (evident) calculele sunt făcute cu o anumită marjă de eroare (şi avem o acurateţe ceva mai bună luând k impar, 401 şi nu 400); următorul mic experiment (în consola R) este suficient de edificator:

> x <- seq(-1.1, 1.1, len = 401)
> sprintf("%.20f", unique(diff(x)))
[1] "0.00550000000000006040" "0.00549999999999983835" "0.00549999999999994937"
[4] "0.00549999999999961631"  # abscisele nu sunt chiar echi-distanţate!
> 0.00550000000000006040 - 0.00549999999999983835 == .Machine$double.eps
[1] TRUE  # ca numere de tip 'double', cele două valori din membrul stâng sunt "egale"
> print(.Machine$double.eps, digits=20)
[1] 2.2204460492503130808e-16  # marja de eroare pentru compararea numerelor "reale"
> dom = outer(x, 1i*x, "+")  # 401x401 puncte (x, y)
> length(dom[abs(Re(dom)) == abs(Im(dom))])
[1] 627  # puncte "diagonale" (teoretic ar fi 2*401)
> dom = outer(seq(-1.1, 1.1, len=400), 1i*seq(-1.1, 1.1, len=400), "+")
> length(dom[abs(Re(dom)) == abs(Im(dom))])
[1] 460  # puncte "diagonale" (pentru 400x400 puncte (x, y))

diff() ne-a dat diferenţele dintre câte două valori consecutive în vectorul x generat de seq(). Majoritatea acestor diferenţe sunt egale, sau diferă prin mai puţin de .Machine$double.eps - "marja de eroare" luată în calcul de operatorul "=="; dar afişând cu câte 20 de zecimale (prin sprintf()), constatăm (folosind unique()) că diferenţele respective au totuşi patru valori "distincte" (pe care testul "==" le găseşte apoi egale, faţă de marja de eroare menţionată).

Apoi, prin outer() am generat câte o grilă pe cele 401 şi respectiv, 400 de abscise "echidistante" - constatând că în primul caz avem un număr sensibil mai mare de "puncte diagonale" (dar mai mic decât 2×401, cum era de aşteptat pentru abscise şi respectiv ordonate, echidistanţate).

Cele evocate mai sus discreditează (exceptând cazul n = 2) această încercare de evidenţiere a punctelor "de excepţie" şi nici n-am mai fi expus lucrurile respective, dacă nu am fi întâlnit ocazia de a ne lămuri asupra unor aspecte numerice (cumva inedite) privitoare la funcţia seq().

Primul caz corespunde polinomului $z^2-1$ şi este singurul despre care putem fi siguri că reflectă corect lucrurile (punctele axei verticale şi numai acestea, sunt "de excepţie"); într-adevăr, Arthur Cayley a stabilit că pentru orice polinom de variabilă complexă de gradul doi, fiecare dintre cele două semiplane (disjuncte) determinate de mediatoarea segmentului rădăcinilor este "bazinul de atracţie" (prin metoda lui Newton) al rădăcinii conţinute în semiplanul respectiv (iar mediatoarea este invariantă: punctele ei "oscilează" pe mediatoare, prin transformarea respectivă).

2. Cum orbitează "punctele diagonale", pentru n = 4k

Dar şi al doilea caz redat mai sus (n = 4) reflectă corect (sau aproape corect) lucrurile: dacă n = 4k, atunci punctele y = ±x orbitează pe bisectoarea respectivă (şi pentru k impar - nu fac parte din bazinul de atracţie al vreuneia dintre rădăcinile unităţii).

Într-adevăr, pentru $g(z)=z^{4k}-1$ avem $$N_g(z)=z-\frac{g(z)}{g'(z)}=\frac{(4k-1)z^{4k}+1}{4kz^{4k-1}}=\frac{(4k-1)z^{4k}+1}{4kz^{4k}}z$$

Pentru punctele $z=x(1 \pm i),~x \in \mathbb R$ aflate pe bisectoarele sistemului de axe, avem $z^4=(\pm 2i)^2x^4=-4x^4\in \mathbb R$ deci multiplicatorul lui $z$ din ultima exprimare de mai sus a lui $N_g(z)$ este număr real - ceea ce înseamnă că $N_g(z)$ are partea reală egală sau de semn contrar cu partea imaginară; prin urmare (pentru n = 4k), $N_g(z)$ transformă punctele "diagonale" în puncte diagonale.

Pentru n = 4k cu k par, avem 4 dintre rădăcinile unităţii chiar pe bisectoarele sistemului de axe; deci în acest caz, punctele "diagonale" nu sunt neapărat, puncte "de excepţie" (putând orbita eventual, spre rădăcina aflată pe bisectoarea respectivă).

Următoarea funcţie returnează rădăcinile de ordin n ale unităţii (folosind formula lui Euler, $\cos\frac{2h\pi}{n}+i\sin\frac{2h\pi}{n}=\mathbf e ^{\boldsymbol {i\,2h\pi/n}}{\textstyle ,~\small h=0..n-1}$) şi o putem folosi eventual pentru a verifica poziţionarea acestora faţă de bisectoarele sistemului de axe:

get_roots1 <- function(n)  exp(1i * 2*pi * (0:(n-1)/n))

print(get_roots1(8))  # n = 4k, cu k par (4 rădăcini sunt pe cele două bisectoare)
[1]  1.0000000+0.0000000i  0.7071068+0.7071068i  0.0000000+1.0000000i
[4] -0.7071068+0.7071068i -1.0000000+0.0000000i -0.7071068-0.7071068i
[7]  0.0000000-1.0000000i  0.7071068-0.7071068i
print(get_roots1(12))  # n = 4k, cu k impar (nu există rădăcini situate pe bisectoare)
 [1]  1.0000000+0.0000000i  0.8660254+0.5000000i  0.5000000+0.8660254i
 [4]  0.0000000+1.0000000i -0.5000000+0.8660254i -0.8660254+0.5000000i
 [7] -1.0000000+0.0000000i -0.8660254-0.5000000i -0.5000000-0.8660254i
[10]  0.0000000-1.0000000i  0.5000000-0.8660254i  0.8660254-0.5000000i

Următoarea funcţie improvizează determinarea orbitei unui punct - simplificând totuşi, calculul lui $N_g(z)$ - şi putem verifica faptul că în cazul "k par", punctele bisectoarelor pot să fie atrase (toate?) de rădăcina lui 1 situată pe bisectoarea respectivă:

orbiting <- function(n=8, max=8, z=1+1i) {
  orbit <- c(z)
  for(it in 1:max)
    orbit <- append(orbit, z <- ((n - 1)*z + z^(1-n)) / n)
  return(orbit)  # orbita lui z, pentru g(z) = z^n - 1 (după 'max' iteraţii)
}

print(orbiting())  # la a 7-a iteraţie se ajunge într-o rădăcină a unităţii (aici, n = 8)
[1] 1.0000000+1.0000000i 0.8828125+0.8828125i 0.7911553+0.7911553i
[4] 0.7325287+0.7325287i 0.7099894+0.7099894i 0.7071474+0.7071474i
[7] 0.7071068+0.7071068i 0.7071068+0.7071068i 0.7071068+0.7071068i

Am verificat pentru câteva puncte ale bisectoarei, în cazul "k impar", că orbita corespunzătoare nu este periodică: dacă orb = orbiting(n=4, max=10000, z=2+2i) ar fi periodică, atunci ar trebui să avem length(orb) > length(unique(orb)) - ori pentru câteva exemple pe care le-am considerat nu am găsit nici o diferenţă (dar iarăşi, nu putem afirma nimic precis).

3. Frumos, sau instructiv? Conturatea "excepţiilor"

Culorile din primul rând de imagini evidenţiază fiecare, punctele cu orbite cam de o aceeaşi lungime. Imaginile mai discrete, de pe al doilea rând, conturează "excepţiile": nuanţele de gri-deschis marchează punctele atrase mai repede sau mai încet de către rădăcini - încât la limită, nuanţa cea mai apropiată de negru vizează punctele rămase în afara zonelor de atracţie.

Funcţia attract() prin care am obţinut asemenea imagini, are acum trei categorii de parametri: ordinul rădăcinilor unităţii, numărul de iteraţii şi "marja de eroare"; domeniul de puncte ale căror orbite se evaluează (limitele părţii reale şi părţii imaginare); respectiv lăţimea ferestrei grafice şi opţiunea de colorare. În funcţie de lăţime şi de limitele domeniului stabilim înălţimea ferestrei şi grila de pixeli pentru care se determină (pentru parametrii de iterare indicaţi) lungimile orbitelor (indicând culorile sau nuanţele de gri care vor fi aplicate pixelilor respectivi, în final):

attract <- function(n = 4, maxit = 200, eps = 1E-8, 
                    dom = c(-1.1, 1.1, -1.1, 1.1),
                    dim_img = 600, colit = FALSE) {
  orbiting <- function(z0) {
    for(it in 1:maxit) {
      if(z0 == 0) return(NA)  # return(maxit+1)
      z1 <- ((n - 1)*z0 + z0^(1-n)) / n  # x - g(x)/g'(x) cu g(x) = x^n - 1
      if(abs(z1 - z0) < eps) return(it)
      z0 <- z1
    }
    return(1)  # return(maxit + 2)
  }
  dx <- dom[2] - dom[1]
  dy <- dom[4] - dom[3]
  asp <- dy / dx  # "aspect-ratio"
  if(dx >= dy) {  # lăţimea  şi înălţimea ferestrei
    width <- dim_img
    height <- ceiling(width * asp)
  } else {
    height <- dim_img
    width <- ceiling(height / asp)
  }
  dx <- dx / width  # "pasul" punctelor, pe orizontală şi pe verticală
  dy <- dy / height
  mz <- apply(outer(0:width, height:0, 
                    function(x, y) dom[1] + x*dx + 1i*(dom[3] + y*dy)), 
              1:2, orbiting)  # "culorile" asociate punctelor prin orbiting()
  if(colit)  # colorează după lungimile orbitelor
    mz <- apply(mz, 1:2, function(z) colors()[2*z  + 1])
  else  # creşte odată cu 'it' de la alb spre negru
    mz <- 17 / (mz + 16)  # valorile din 'mz' sunt >=1 (sau 'NA')
  plot(as.raster(t(mz)))
}

În [1] vizam doar domenii "pătratice", fiindcă ne bazam doar pe o secvenţă de abscise (dată ca parametru); acum putem considera orice domeniu (dreptunghiular), iar densitatea punctelor poate fi reglată prin parametrul 'dim_img' (dimensiunea cea mai mare a ferestrei grafice).

Angajând plot.raster() - şi nu plot() ca în [1] - ne-am scutit acum, de a alege valori potrivite pentru parametrii specifici punctelor (formă şi mărime). Într-un obiect "raster", pixelii sunt înregistraţi pe linii, de sus în jos - încât a trebuit să "inversăm" ordonatele (de la 'height' spre 0) şi să transpunem în final (prin funcţia t()) matricea respectivă.

Valorile înregistrate în matricea 'mz' sunt lungimile orbitelor (returnate pentru fiecare punct, din funcţia interioară orbiting()); pentru cazul apelului cu 'colit = TRUE', am înlocuit aceste valori cu nume de culori din vectorul returnat de funcţia colors() (iar plot.raster() va colora corespunzător, punctele respective). Pentru celălalt caz ('colit = FALSE') am inversat valorile respective - încât bazinelor de atracţie (unde numărul de iteraţii este mic) le vor corespunde nuanţe de gri-deschis, iar punctelor "de excepţie" (pentru care numărul de iteraţii este mare) le vor corespunde nuanţe de gri-închis; dar inversând "mot-a-mot" mz = 1 / mz, nuanţele respective erau prea apropiate între ele - încât am exersat cu nişte coeficienţi, ajungând la mz = (1 + 16) / (mz + 16).

Mărind 'dim_img', valorile 'dx' şi 'dy' se vor micşora - încât numărul de puncte "echidistanţate" luate în calcul va creşte (sporind detaliile imaginii finale, cu preţul unei creşteri a timpului de execuţie). Pentru n > 4, numărul de iteraţii care se va indica în 'maxit' trebuie mărit; eventual, 'eps' trebuie micşorat (spre .Machine.double$eps ≈ 2.220446e-16).

4. O operaţie de mărire (detaliile imită întregul)

Vrem să evidenţiem grafic o anumită caracteristică a structurilor de puncte redate (pe un număr finit de puncte) prin imaginile obţinute printr-un apel attract(): "detaliile imită întregul" (dar vezi self-similarity). Procedăm simplu (fără animaţie): după ce utilizatorul ar bifa două colţuri opuse ale unei zone dreptunghiulare din cadrul imaginii, reapelăm attract() pentru zona respectivă; faţă de câte se considerau iniţial, acum vor fi luate în calcul mai multe puncte ale zonei respective - obţinând o mărire "veritabilă" (nu doar "zoom-in") a acelui detaliu:

A doua imagine (în care am adăugat două puncte roşii, în capetele celei de-a doua diagonale) "măreşte" zona dreptunghiulară ale cărei colţuri au fost bifate (cu roşu) în prima imagine. Prin asemenea operaţii de mărire, începe să devină clară asemănarea dintre structura detaliului şi structura "întregii" imagini… (dar aspectele teoretice subiacente sunt dificile, de înalt nivel şi în continuă dezvoltare, de prin 1920 încoace; a vedea eventual, Julia set şi Chaos theory).

Folosind dev.new() şi dev.set() vom putea opera pe rând, în mai multe ferestre grafice (pentru imaginea de bază şi respectiv, pentru detalii). Anulăm marginile ferestrelor (rezervate în mod implicit, pentru gradarea şi etichetarea axelor şi pentru titluri); mai ţinem cont de faptul că în mod implicit, plot() extinde intervalul valorilor de plotat (cu 4%, la ambele capete) şi evităm aceasta folosind prin funcţia par() parametrii grafici 'xaxs' şi 'yaxs' (setându-i pe valoarea "i").

Folosim apoi funcţia locator(); aceasta va "citi" poziţia cursorului grafic al mouse-ului, returnând o listă cu două componente ($'x' şi $'y'), reprezentând coordonatele în cadrul ferestrei grafice ale punctelor "citite". Coordonatele respective sunt relative la valorile din vectorul par("usr") (limita inferioară şi cea superioară, pentru abscisele şi pentru ordonatele pixelilor); desigur, aceste coordonate-ecran trebuie mapate pe domeniul de "orbitat" prin funcţia attract():

show_detail <- function(n = 6, maxit = 200, eps = 1E-8, 
                        dom = c(-1, 1, -1, 1), width = 600) {
  dev.new()
  opar <- par(mar=c(rep(0, 4)), xaxs="i", yaxs="i")
  w1 <- dev.cur()
  dev.new()
  opar <- par(mar=c(rep(0, 4)), xaxs="i", yaxs="i")
  w2 <- dev.cur()
  dev.set(w1)  # în prima fereastră: imaginea "întreagă"
  attract(n=n, maxit=maxit, eps=eps, dom=dom, dim_img=width)
  usr_wh <- par("usr")[c(2, 4)] - par("usr")[c(1, 3)]
  dom_wh <- dom[c(2, 4)] - dom[c(1, 3)]
  loc <- locator(n=2, type="p", pch=20, col="red")
  # mapează pe 'dom' coordonatele-ecran ale punctelor "bifate" 
  x <- loc$x * dom_wh[1] / usr_wh[1] + dom[1]
  y <- loc$y * dom_wh[2] / usr_wh[2] + dom[3]
  sub_dom <- c(x, y)  # subdomeniul corespunzător punctelor "bifate"
  dev.set(w2)  # în a doua fereastră: imaginea detaliului indicat
  attract(n=n, maxit=maxit, eps=eps, dom=sub_dom, dim_img=width) 
}

## exemplu (pentru cele două imagini redate mai sus):
show_detail(n=6, maxit=1000, eps=2.220446e-16, dom=c(-1, 1, -1, 1), width=600)

Nu se poate să nu remarcăm că în prima imagine avem o dungă verticală albă (nu gri, ca pentru bazinele de atracţie); ea ar corespunde liniei verticale colorate "magenta", din a treia imagine (tot pentru n = 6) de la §1 şi a apărut astfel acum, fiindcă în funcţia orbiting() (v. §3) am returnat "NA" pentru cazul când la iterarea curentă avem z0 == 0 (iar valorile "NA" sunt redate prin "alb" sau "transparent", de către plot.raster()). Aveam alternativa (menţionată în comentariul adăugat liniei respective) de a returna (maxit + 1); atunci ar rezulta o dungă verticală neagră (nu o nuanţă spre negru, ca pentru punctele "de excepţie").

Am deduce de aici că pentru n = 6, punctele axei imaginare oscilează de-a lungul acesteia, tinzând cumva spre 0 (sau spre infinit). Să observăm că din punctul curent z se ajunge în 0 numai dacă z este rădăcină a ecuaţiei $N_g(z)=0$ - de unde am zice, ideea de a genera fractalul iterând în sens invers de la 0 (găsind zerourile lui $N_g()$, apoi preimaginile acestora, etc.); în "partea a doua" ne propunem să speculăm această idee (dar fie spus - nu este nici ea nouă).