Generarea expresiilor aritmetice cu patru operanzi
[1] Find all expressions that evaluate to some value [google Mishoo]
[1] instituie o anumită infrastructură javaScript, pentru a identifica expresiile aritmetice de valoare dată, cu operanzi distincţi. Un joc aritmetic educativ - 24 Game - angajează patru operanzi 1..9 şi cere o expresie aritmetică de valoare 24 (numărul de ore ale zilei).
Aici modelăm expresiile aritmetice prin arbori binari, plecând de la o clasă abstractă C++ pentru noduri şi angajând "smart pointers" din C++11.
Expresiile aritmetice cu 4 operanzi şi 3 operatori
Orice expresie aritmetică poate fi reprezentată printr-un arbore binar; pentru patru operanzi, avem următoarele cinci posibilităţi:
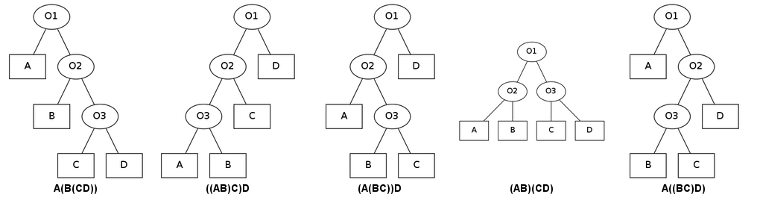
Astfel, A(B(CD)) reprezintă expresiile "A O1 (B O2 (C O3 D))", unde prin Oj indicăm una dintre cele patru operaţii aritmetice elementare (de exemplu, 2/(3*(5+6)).
Pentru operanzi avem 4! = 24 de posibilităţi de angrenare în cadrul expresiei (valorile A, B, C, D sunt date, dar pot fi permutate); cei trei operatori pot să aibă fiecare, una dintre valorile ['+', '-', '*', '/'] - în total 43 = 64 de posibilităţi. Rezultă că avem un număr de 4!*43*5 = 7680 expresii posibile; unele dintre acestea vor fi eventual invalide (conducând la "împărţire cu zero").
Acest calcul este valabil numai în cazul când cei 4 operanzi sunt distincţi între ei; altfel, am avea "permutări cu repetiţie" şi rezultatul trebuie scalat corespunzător. De exemplu, pentru [3, 3, 8, 8] avem numai 4!/(2!*2!) = 6 permutări (distincte) - încât în acest caz (când numai doi operanzi sunt distincţi) vom avea doar 7680/4 = 1920 expresii posibile.
Pentru generarea efectivă a acestor expresii ar fi de dorit (dar aici vom ignora acest aspect) să ţinem seama de comutativitatea operaţiilor '+' şi '*' - considerând că expresii ca:
(8/(3*(3+8))) Tree('+', 3, 8) == Tree('+', 8, 3) (8/(3*(8+3))) (8/((3+8)*3)) Tree('*', Tree t1, 3) == Tree('*', 3, Tree t2) dacă t1 == t2 (8/((8+3)*3)) = 0.242424 = 0.(24) Apropo… despre 24 era vorba!
sunt "identice", impunând redarea doar a uneia dintre ele. Vom defini mai departe clasa "Tree", încât Tree(o, L, R) să construiască un arbore cu rădăcina o, corespunzător expresiei "L o R" - ignorând însă redefinirea operatorului "==" (necesară, dacă am viza numai expresiile semnificative).
Modelare C++ pentru arbori aritmetici
Nodurile interne corespund operatorilor din cadrul expresiei, fiecare având de înregistrat operatorul respectiv şi cele două subexpresii operate de acesta; frunzele arborelui reprezintă operanzii numerici ai expresiei. Clasa de bază Node() specifică metodele print() şi eval() - de redefinit după caz, în clasele derivate Operator() şi Operand().
Modelăm expresiile şi sub-expresiile prin clasa Tree(), conţinând un pointer sptr la instanţa curentă de Node(); atunci, sptr->eval() şi respectiv sptr->print() vor invoca metodele specifice tipului curent de "Node" - fie Operator::eval()/print(), fie Operand::eval()/print().
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 | /* fişierul ar_exp.h */ #include <ostream> #include <iostream> #include <memory> // std::shared_ptr, std::make_shared ("smart pointers", C++11) class Tree; // Tree() va trebui să poată accesa metodele Node() class Node { friend std::ostream& operator<<(std::ostream&, const Tree&); friend class Tree; // Tree::eval() va putea accesa Node::eval() protected: virtual double eval() const = 0; virtual void print(std::ostream&) const = 0; }; class Tree { friend std::ostream& operator<<(std::ostream&, const Tree&); std::shared_ptr<Node> sptr; // "pointer" la rădăcina arborelui public: Tree() {} Tree(double); // construieşte un "operand" Tree(char, Tree, Tree); // construieşte un "operator" double eval() const { return sptr->eval(); // invocă Node::eval(), pentru instanţa curentă de Node() } }; class Operator: public Node { public: Operator(char binop, Tree left, Tree right) : binop(binop), left(left), right(right) {} private: char binop; // '+', -', '*', sau '/' Tree left, right; // subarborii pe care operează double eval() const; void print(std::ostream& out) const { // out << "(" << left << binop << right << ")"; // "infix", cu paranteze out << left << ' ' << right << ' ' << binop << ' '; // RPN (forma poloneză) } }; class Operand: public Node { public: Operand(double d) : value(d) {} private: double value; double eval() const { return value; } void print(std::ostream& out) const { out << value; } }; |
Operatorul "<<" - redefinit la linia 54 (vezi mai jos) - trebuie declarat "friend" (care nu este relaţie tranzitivă) şi clasei Tree() (linia 16) şi clasei Node() (linia 8) - pentru a putea accesa Tree::sptr şi (prin intermediul acestui "pointer") metodele din Node().
Nu este necesară prevederea unui destructor (virtual) în clasa Node(), fiindcă nu vom implica direct new(), ci vom folosi std::make_shared() (liniile 59 şi 62) - aceasta invocă ea însăşi new(), alocând şi construind un obiect de tipul indicat; însă devine necesar un constructor public pentru acest obiect şi din acest motiv, constructorii de Operand() şi Operator() (liniile 29 şi 43) au fost declaraţi "public" - altfel, era firesc "private" dat fiind că existenţa acestor obiecte (operatori şi operanzi) are sens numai în cadrul expresiei care le angrenează, nu şi în exterior (ca obiecte independente).
50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 | /* fişierul ar_exp.cpp */ #include "ar_exp.h" #include <limits> // numeric_limits std::ostream& operator<<(std::ostream& out, const Tree& expr) { expr.sptr->print(out); return out; } Tree::Tree(double d): sptr(std::make_shared<Operand>(d)) {} Tree::Tree(char binop, Tree left, Tree right) : sptr(std::make_shared<Operator>(binop, left, right)) {} double Operator::eval() const { double val_1 = left.eval(); double val_2 = right.eval(); switch(binop) { case '+': val_1 += val_2; break; case '-': val_1 -= val_2; break; case '*': val_1 *= val_2; break; case '/': try { if(val_2) val_1 /= val_2; else { val_1 = std::numeric_limits<double>::max(); throw "INVALID: "; // divide by zero } } catch(const char* str) {std::cout << str;} } return val_1; } |
Intenţionând să generăm toate expresiile posibile, am prevăzut prefixarea cu "INVALID" (secvenţa 74-77) a acelora care conduc la "divide by zero" - evaluate aici conform principiului "1/0 = ∞".
Pentru un exemplu simplu, de folosire a claselor definite de mai sus:
(6 / (1 - (3/4)))
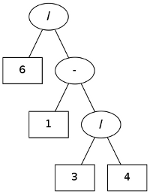
#include "ar_exp.h" // --std=gnu++0x (C++11 pe g++ 4.6.3) int main() { Tree t = Tree('/', 6, // conversie implicită Tree(6) Tree('-', 1, Tree('/', 3, 4 ) ) ); std::cout << t << " = " << t.eval() << '\n'; }
vb@vb:~/TREES$ g++ --std=gnu++0x -o test ar_exp.cpp ar_test.cpp vb@vb:~/TREES$ ./test 6 1 3 4 / - / = 24 // Sau în formă infixată: (6/(1-(3/4))) = 24
Bineînţeles că scrierea normală ar fi fost Tree t = Tree('/', 6, Tree('-', 1, Tree('/', 3, 4)));, dar forma redată mai sus evidenţiază (indentând pe linii separate) subarborii constituenţi.
Obţinerea şi filtrarea expresiilor cu 3 operatori şi 4 operanzi
Scopul firesc ar fi acela de a obţine expresiile de valoare dată (valoarea tipică fiind 24); am putea folosi metoda backtracking, după modelul din [1] - dar nu vedem totuşi, cum s-ar putea evita investigarea tuturor variantelor posibile. De aceea, preferăm să explicităm toate expresiile posibile, filtrând apoi (folosind de exemplu grep) pe acelea care ne interesează.
Funcţia phrase() constituie (şi afişează) expresiile de cele cinci tipuri evidenţiate mai sus, pentru toate permutările furnizate de std::next_permutation() pe cele 4 numere transmise:
// g++ --std=gnu++0x -O2 -o all_exp ar_exp.cpp all_exp.cpp #include "ar_exp.h" #include <algorithm> // std::next_permutation() void phrase(int num[]) { static char opt[] = {'+', '-', '*', '/'}; Tree h[5]; // 5 tipuri de expresii (cu 4 numere) for(char o1: opt) // C++11 for(char o2: opt) for(char o3: opt) { do{ h[0] = Tree(o1, num[0], // conversie implicită la Tree(num[0]) Tree(o2, num[1], Tree(o3, num[2], num[3]))), h[1] = Tree(o1, Tree(o2, num[0], Tree(o3, num[1], num[2])), Tree(num[3])), h[2] = Tree(o1, Tree(o2, num[0], num[1]), Tree(o3, num[2], num[3])), h[3] = Tree(o1, Tree(num[0]), Tree(o2, Tree(o3, num[1], num[2]), num[3])), h[4] = Tree(o1, Tree(o2, Tree(o3, num[0], num[1]), num[2]), num[3]); for(int i=0; i < 5; ++i) std::cout << h[i] << " = " << h[i].eval() << '\n'; }while(std::next_permutation(num, num+4)); } } int main() { int nums[][4] = {{1,3,4,6}, {3,3,8,8}}; //, {1,4,5,6}, {4,1,9,7}}; for(unsigned int i=0; i < 2; i++) phrase(nums[i]); }
Compilăm şi executăm, extrăgând prin grep numai liniile încheiate cu "=24":
vb@vb:~/TREES$ g++ --std=gnu++0x -O2 -o all_exp ar_exp.cpp all_exp.cpp vb@vb:~/TREES$ ./all_exp | grep "= 24$" 6 1 3 4 / - / = 24 # 6 / (1 - 3/4) unic! 8 3 8 3 / - / = 24 # 8 / (3 - 8/3) unic!
Dacă ne-ar interesa şi alte lucruri (câte expresii, câte sunt invalide, etc.), atunci este preferabil să redirectăm ieşirea către un fişier - evitând să reexecutăm programul (după modelul redat mai sus) pentru fiecare nou criteriu de filtrare:
vb@vb:~/TREES$ ./all_exp > all_exp.txt vb@vb:~/TREES$ grep "= -24$" all_exp.txt 6 3 4 / 1 - / = -24 # 6 / (3/4 - 1) = -24 8 8 3 / 3 - / = -24 vb@vb:~/TREES$ wc -l all_exp.txt 9600 all_exp.txt vb@vb:~/TREES$ grep -c "INVALID" all_exp.txt 42
Am obţinut în "all_exp.txt" 9600 de expresii (wc -l ne-a dat numărul de linii din fişier), între care 42 invalide; într-adevăr, pentru {1,3,4,6} avem 7680 expresii posibile (cum am arătat la început), iar pentru {3,3,8,8} avem 1920 (şi 7680 + 1920 = 9600).
vezi Cărţile mele (de programare)