"Hello World!"
În anul 2008 se vor împlini 30 de ani de la apariţia primei cărţi de prezentare a limbajului C, scrisă de chiar creatorii limbajului, Brian Kernighan şi Dennis Ritchie, cu titlul The C Programming Language (Copyright © 1978 by AT&T Bell Laboratories). Primul exemplu de program C redat în carte este acesta:
main() { printf("hello, world\n"); }
De atunci începând, cam orice prezentare de limbaj de programare începe cu un program în limbajul respectiv care dacă ar fi executat de "maşină", n-ar face altceva decât să afişeze "Hello World!".
O problemă de programare pentru orice limbaj
Ne-am propus să imităm ideea de a formula în diverse limbaje de programare, soluţionarea unei aceleiaşi probleme (şi anume, printr-un acelaşi algoritm). Am ales în acest scop problema calculării factorialului unui număr natural, conform binecunoscutei definiţii recursive:
$$n!=\begin{cases}1& \text{if}\; n==1\\n(n-1)!& \text{if}\; n\gt 1\end{cases}$$Iată o exemplificare a procesului de calcul:
4!
= 4 * 3!
= 4 * (3 * 2!)
= 4 * (3 * (2 * 1!))
= 4 * (3 * (2 * 1)) =
= 4 * (3 * 2)) =
= 4 * 6 =
= 24
Bineînţeles, acest rezultat se obţine mult mai simplu calculând mintal! Dar problema noastră constă în a calcula de exemplu, valoarea 100! sau chiar 12345! - nu 3! = 1*2*3 şi nici măcar 10!.
Este de la sine înţeles că nu ne-am propus să furnizăm doar listingurile programelor; vom prezenta aspecte semnificative de lucru într-un limbaj sau altul, cu diverse corelări între limbaje sau cu sistemul de operare; vom evidenţia (dar aceasta, inclusiv în comentariile din cadrul programelor redate) aspecte de elaborare şi aspectele algoritmice necesare.
În majoritatea limbajelor, va fi necesară o mică modelare suplimentară de "operaţii cu numere mari". Este firesc să începem prin a lămuri totuşi, despre ce vorbim - să vedem întâi câte cifre are numărul n! (unde "cifre", nu înseamnă neapărat cifre zecimale) pe care vrem să-l calculăm şi care ar fi atunci, cea mai potrivită bază pentru operare.
Lungimea factorialului
n! este un produs de numere, iar logaritmul produsului este egal cu suma logaritmilor factorilor:
$$\log(n!)=\sum_{k=2}^{n}\log(k)$$De exemplu, log10(10!) = 6.559763; caracteristica fiind 6, rezultă că 10! are 7 cifre şi căutând în tabelul de logaritmi zecimali mantisa 0.559763, găsim primele cifre al lui 10!, anume 10! = 3628... (deci 10! are lungimea 7, primele cifre fiind 3628).
Desigur, trebuie să "automatizăm" acest procedeu, dacă vrem să găsim şi pentru 100! de exemplu, "câte cifre are şi care sunt primele câteva". Următoarea funcţie javascript poate rezolva chestiunea.
function factorial_inform( n ) { // privind numărul n! (factorialul lui n) var lgf = 0; // suma logaritmilor zecimali ai factorilor 2, 3, ..., n var est = Math.pow(10, 7); // estimează numărul primelor cifre exacte (7) var thend = "..."; // urmează alte cifre după cele estimate exact for(var k=2; k <= n; k++) { lgf += Math.log( k ) / Math.LN10; // log în baza 10, lg(k) = LN(k) / LN(10) } var len = parseInt( lgf ); // caracteristica logaritmului în baza 10 a lui n! if(len < 15) { est = Math.pow(10, len); thend = ""; } // "len" cifre exacte var mantisa = parseFloat( lgf ) - len; // mantisa logaritmului lui n! len++; // numărul de cifre ale lui n! var cifre = parseInt( Math.pow(10,mantisa) * est ); // primele "est" cifre în n! alert(n + "! are " + len + " cifre zecimale\n" + n + "! = " + cifre + thend); }
Ca exemplu, 450! are 1001 cifre zecimale şi 450! = 17333687...
există n încât n! să aibă 1000 cifre zecimale?
există n încât n! să aibă n cifre zecimale? (da: 22, 23, 24)
Baza de operare cea mai potrivită
Un număr cu 100 de cifre zecimale ocupă (de obicei) 100 de "locaţii"; fiecare locaţie înregistrează o cifră zecimală (0..9). Orice operaţie care angajează acest număr (de exemplu, adunarea lui cu un alt număr de 100 de cifre) trebuie să efectueze 100 de operaţii elementare "cifră-cu-cifră".
Să presupunem acum că în "locaţie" încap 2 cifre zecimale: (00)..(99); atunci numărul nostru de 100 de cifre zecimale, poate fi înregistrat folosind 50 de locaţii, iar operaţiile care ar implica numărul ar necesita 50 de "operaţii elementare" între conţinuturile locaţiilor (desigur, ar trebui să folosim table de operare - tabla adunării, tabla înmulţirii - cu "cifre" 00-99, în loc de cele obişnuite cu cifre 0-9).
În primul caz, am folosit baza de numeraţie uzuală - baza 10 (cu cifre 0..9, numite "cifrele zecimale"); în al doilea caz am folosit baza 100, având drept "cifre" valorile 0, 1, 2, ..., 9, (10), (11), ..., (99). Se vede şi pe aceste exemple, că atât în privinţa spaţiului necesar reprezentării, cât şi în privinţa timpului de execuţie necesar operării - este mai avantajos de folosit o bază de numeraţie mai mare, decât una "mică".
Memoria calculatorului este constituită din "locaţii" care au dimensiunea standard de 8 biţi; pe un bit se poate înregistra fie valoarea 0, fie valoarea 1; pe doi biţi se pot deci înregistra cele 22 perechi de biţi (00), (01), (10) sau (11) - adică, reprezentând în baza uzuală, valorile 0, 1, 2, 3; pe trei biţi… - ş.a.m.d. Într-o locaţie de memorie de 8 biţi se pot înregistra valori 0..255 (fiindcă 28 = 256).
Cam toate operaţiile interne ale calculatorului - transfer de date, operaţii aritmetice, etc. - se bazează pe faptul că "unitatea de măsură" este locaţia de 8 biţi; nu se accesează şi nu se transferă biţi individuali, ci întreaga locaţie (sau locaţiile care conţin biţii respectivi); nu se operează bit-cu-bit, ci "locaţie-cu-locaţie". O instrucţiune precum ADD AX, BX consumă acelaşi timp pentru execuţia ei atât în cazul când locaţiile AX şi BX conţin respectiv valoarea 1 (pentru e efectua adunarea 1+1), cât şi în cazul în care AX=234 şi BX=159.
Aluziile prezentate vor să evidenţieze că modelarea numerelor mari ar trebui întreprinsă folosind baza 256 (sau eventual, baza 216) şi nu baza uzuală 10. Avem şi următorul raţionament elementar: cel mai mare număr natural care are Z cifre zecimale este 10Z - 1; cel mai mare număr natural care are T cifre în baza 256 (acestea se cheamă octeţi, sau bytes) este 256T - 1; ca să vorbim de aceleaşi numere naturale şi într-o bază şi în cealaltă, trebuie să avem 10Z = 256T; aplicând logaritmii zecimali, rezultă: Z = T * lg(256) ≈ T * 2.40824.
Adică, reprezentarea în baza 256 necesită de minimum 2.4 ori mai puţine "locaţii" decât cea în baza 10, iar operarea bazată pe reprezentarea în baza 256 necesită de 2.4 ori mai puţine operaţii "cifră cu cifră" decât cea bazată pe reprezentarea zecimală obişnuită. De exemplu, un număr cu 100 de cifre zecimale va fi reprezentat în baza 256 pe maximum [100 / 2.4] + 1 = 42 de octeţi.
Evaluarea performanţei
Dacă decidem să operăm în baza 256, atunci pe de o parte, va fi nevoie de o funcţie suplimentară, dar care nu va fi apelată decât într-un singur punct: la scrierea în forma zecimală uzuală a rezultatului final (conversie nu tocmai simplă, fiindcă e vorba de numere mari).
Să încercăm să evaluăm şi performanţa de calcul rezultată: la fiecare pas avem de înmulţit un număr din ce în ce mai mare, anume (k-1)!, cu un număr "obişnuit" k, deci operând în baza 256 pentru a calcula n!, facem o economie de operaţii de tip "cifră cu cifră" care pare a fi de ordinul n / 2.4.
Dacă acceptăm această evaluare (evident grosolană), atunci… să fim realişti: pentru 100000! am face o economie de vreo 42000 operaţii, ceea ce este deja nesemnificativ de vreme ce un calculator obişnuit face milioane de operaţii pe secundă… Astfel că, din punct de vedere practic devine suficient să rămânem la nivelul de operare uzuală, cea de bază 10; poate aşa vom şi face—dar nu datorită evaluării închipuite aici….
În realitate, estimarea de mai sus este oribilă ("grosolană" este prea blând); nu n trebuie raportat la 2.4, ci lungimea factorialului (vezi mai sus, formula de legătură stabilită între Z şi T).
Să presupunem că am ajuns cu calculul la 450! şi urmează înmulţirea acestei valori cu 451, ceea ce implică următoarea operaţie individuală: se înmulţeşte 451 cu cifra curentă şi se adună transportul de la precedenta înmulţire; această operaţie individuală trebuie începută de la cifra unităţilor şi trebuie repetată de atâtea ori câte cifre are "deînmulţitul" - deci de 1001 ori în cazul reprezentării în baza 10, respectiv de vreo [1001 / 2.4] = 417 ori în cazul reprezentării în baza 256.
"Economia de operaţii" vizată (iarăşi în mod greşit!) de "evaluarea" de mai sus, înseamnă de fapt diferenţa dintre numărul de operaţii individuale necesare în cele două baze, adică ar fi de 1001 - 417 = 584 de operaţii individuale - pe când evaluarea citată indică (şi încă pentru întregul calcul de factorial) o "economie" de 451/2.4 = 188 operaţii (departe şi de 584 de operaţii, şi de 417 - cu atât mai mult cu cât "188" se referea la întregul calcul, iar "584" se referă la un anumit pas de pe parcursul calculului factorialului).
Mai departe, prin înmulţirea de mai sus am obţinut 451! şi urmează să înmulţim această valoare cu următorul factor 452; numărul de operaţii individuale necesare este în jur de 1003 în baza 10 şi de vreo 1003/2.4 = 418 în baza 256; înseamnă că iarăşi avem o economie de operaţii individuale şi aceasta trebuie cumulată cu cea precedentă ş.a.m.d., pentru a determina ce economie totală de operaţii are loc dacă lucrăm în baza 256. Putem abstractiza acest calcul astfel:
total_op_10 = 0;
for (k = 2; k <= n; k++) {
total_op_10 += nr_cifre_10 (k!)
}
economie_op_256 = total_op_10 — (total_op_10 / 2.4) = 0.583 * total_op_10
Acest calcul poate fi modelat preluând din funcţia factorial_inform() redată mai sus elementele necesare, prin următoarea funcţie javascript:
function total_op_10( n ) { var toz = 0; var ln10 = Math.LN10; // să accesăm constanta respectivă o singură dată! // (nu ca în 'factorial_inform()', mai sus) for(var factor = 2; factor < n; factor++) { var lgf = 0; // nr. cifre zecimale (operaţii în baza 10) = // = [lg(factor!)] + 1 ≈ Math.ceil(factor!) for(var k = 2; k <= factor; k++) { lgf += Math.log(k) / ln10; } toz += Math.ceil(lgf); // contorizează operaţiile la înmulţirea cu 'factor' } return toz; } function get_diff( nr ) { // nr = numărul al cărui factorial se investighează var toz = total_op_10( nr ); alert("Total operaţii zecimale = " + toz + "\nîn baza 256 vor fi cam cu " + Math.floor(0.583*toz)+" mai puţine"); }
Avem această mică verificare: pentru 450! obţinem 203084 operaţii zecimale, iar pentru 451! obţinem 204085 - şi vedem că diferenţa este 1001, adică exact lungimea zecimală a factorialului de 450 (când 450! se înmulţeşte cu 451, pentru a găsi în final 451! - se mai fac exact aceste 1001 operaţii elementare); verificarea "ţine" şi pe alte cazuri, de exemplu pentru 1000! - dar timpul de execuţie creşte sensibil.
Aaa… dar să nu uităm să precizăm: pentru calculul lui 450! în baza 256 se fac cu 118397 mai puţine operaţii, decât se fac în baza 10; iar pentru 1000! cu peste 106 mai puţine.
Desigur, în calculul prezentat intervin erori de rotunjire, poate—cumulat—şi de ordinul a câteva sute de operaţii (acestea au fost numărate); dar şi-aşa credem, devine clar că modelarea operaţiilor cu numere mari, în baza 256 este categoric mai eficientă decât în baza 10 şi nu numai în sens teoretic, cum învederam în paragraful anterior!
1) bc - An arbitrary precision calculator language
bc programming language este specializat pentru calcule cu numere mari; acestea sunt modelate folosind baza 10 (după cum zice documentaţia…).
/* fişierul "bc-fact" defineşte funcţia fact() */
define fact(n) {
if(n == 1) return 1;
return n * fact(n-1);
}
/* fişierul "bc-fact.app" foloseşte funcţia fact() */
for(n = 100; n <= 1000; n += 100) {
print n, "! = ", fact(n), "\nşi are ", length(last), " cifre\n\n"
}
quit /* redă controlul shell-ului din care s-a lansat execuţia programului 'bc' */
/* variabila predefinită 'last' păstrează ultimul număr printat */
Pentru a rula aplicaţia din 'bc-fact.app' trebuie invocat 'bc' din linia de comandă, indicând ca argumente cele două fişiere:
vb@debian:~/lar$ bc bc-fact bc-fact.ap > bc-fact.out
">" redirectează ieşirea către fişierul 'bc-fact.out' (altfel ieşirea se face pe ecran).
ScienceSoft.at oferă posibilitatea folosirii interactive a interpretorului bc (probabil, prin intermediul bibliotecii libbcmath din PHP). Modulul Inline::BC compilează şi execută cod bc într-un program perl.
bc operează în baza 10?
În manualele uzuale se spune—simplificare, desigur—că bc operează folosind baza 10; dar "bc was implemented on top of dc". La bell-labs.com Bell Laboratories, găsim manualul (din 1965) DC - An Interactive Desk Calculator, de unde cităm: "DC works like a stacking calculator using reverse Polish notation"…; "A language called BC has been developed which accepts programs written in the familiar style of higher-level programming languages and compiles output which is interpreted by DC". Iar apoi:
Internal Representation of Numbers Numbers are kept in the form of a string of digits to the base 100 stored one digit per byte (centennial digits). The string is stored with the low-order digit at the beginning of the string. For example, the representation of 157 is 57,1.
Prin urmare, bc nu operează în baza 10, ci în baza 100; în baza 10, pe fiecare "locaţie" (octet de memorie) stă o singură cifră zecimală, în timp ce în baza 100 pe un octet se memorează două cifre zecimale (constituind împreună "a centennial digit"); în baza 10 se operează cu cifre 0..9, în timp ce în baza 100 unitatea de operare se extinde la domeniul valorilor 00..99 (viteza de operare se dublează, faţă de baza 10). Microprocesoarele dispun şi de instrucţiuni specifice BCD—Binary Coded Decimal care permit operarea eficientă cu numere date în baza 100 (cam de acelaşi nivel de eficienţă cu operarea obişnuită, în baza 256).
Ca de obicei, povestea ne spune că ideile de astăzi nu s-au născut dintrodată; până la a atinge nivelul actual, au existat mereu încercări în diverse direcţii, mai mult sau mai puţin reuşite în funcţie şi de nivelul tehnicii. "Locaţiile" n-au avut dintrodată 8/16/32 biţi, un timp au fost numai de 4 biţi; microprocesoarele n-au avut dintrodată regiştri şi magistrale de 16/32 de biţi, un timp s-a lucrat doar pe 8 biţi; limbajul C n-a apărut nici el dintrodată, un timp s-a lucrat chiar şi numai în cod maşină.
Există şi în continuare direcţii greşite, este firesc - dar de multe ori, cramponarea pe direcţii greşite se datorează neglijării istoriei domeniului (învăţământul informatic - cel prefigurat oficial pe licenţe Microsoft şi pe "point-and-click" - degenerează din ce în ce mai mult, din această cauză).
2) PHP
php (php4, php5) încorporează biblioteca BCMath—Arbitrary Precision Mathematics Functions ("libbcmath") care permite operarea cu numere de orice lungime (reprezentate ca şiruri); funcţia bcmul($a, $b) returnează produsul $a*$b.
<?php function fact($n) { return $n == 1 ? 1 : bcmul( $n, fact($n - 1) ); } $r = fact(10000); // 10000! echo $r . "\n" . strlen($r) . "cifre\n"; ?>
Programul - scris într-un fişier "factorial.php" - poate fi rulat nu numai printr-un web-server (Apache, Microsoft IIS, etc.), dar şi din linia de comandă (PHP CLI—Command Line Interface): php factorial.php.
Merită văzută, ideea care a stat la baza creării limbajului PHP (Rasmus Lerdorf, 1994): se analizează (folosind un parser - acesta a fost scris iniţial în perl, apoi în C) textul unui fişier HTML şi când se întâlneşte un anumit tag (acesta a devenit până la urmă "<?") se inserează în text (în locul tagului respectiv) rezultatul returnat de funcţia indicată sub acel tag (funcţia respectivă fiind executată pe server, nu în browser ca în cazul limbajului javascript). Această idee este folosită în fond şi de alte sisteme de modificare dinamică a paginilor Web (Template::Toolkit în perl, limbajul XSLT încorporat în browserele moderne, etc.), apărute şi acestea în ultimii 10 ani.
3) javascript
JavaScript a fost creat - în 1995, de către Brendan Eich - cu scopul principal de a încorpora într-o pagină HTML funcţii care să fie executate de către browser şi care să asigure interacţiuni între obiectele paginii şi acţiunile utilizatorului.
Ideea că programele respective pot fi rulate chiar din browser, ar trebui să dea de gândit celor care decid "programele şcolare" de informatică; este mai uşor, mai atractiv şi mai productiv (în privinţa perspectivelor) de a începe cu HTML, elemente de DOM—Document Object Model şi javascript decât de a începe (şi încă din clasa a VI-a!) cu "Borland C++ 3.1" (şi-atât!).
În baza 10, iterativ
Întâi propunem un program pentru calculul factorialelor folosind baza 10; se va constata (de exemplu pentru 999!) că "durează" (minimum câteva secunde), chiar şi în varianta iterativă propusă.
function factorial( n ) { var cf = new Array(); // tabloul cifrelor factorialului numărului n cf[0] = 1; // iniţializează cu factorialul lui 1 (1! = 1) for( var f = 2; f <= n; f++) { // factorul cu care trebuie înmulţit cf[] anterior var t = 0; // transportul curent; se propagă de la operaţia (f*cifră) precedentă for(var i = 0, s = cf.length; i < s; i++) { // Începând cu cifra unităţilor, var p = cf[i] * f + t; // înmulţeşte cu factorul curent f, adună transportul, cf[i] = p % 10; // şi înscrie în cf[i] cifra unităţilor produsului. t = Math.floor(p / 10); // noul transport } while(t) { // Dacă terminând înmulţirea cu f, există transport final (nenul), cf[s++] = t % 10; // atunci adaugă în cf[] şi cifrele acestui transport. t = Math.floor(p / 10); } } return cf.reverse().join(''); // inversează tabloul cifrelor şi-l returnează ca şir }
Programul redat lămureşte algoritmul de care vom avea nevoie: presupunând că s-a determinat (f-1)! în cf[], pentru a determina mai departe şi pe f! urmează să se facă cel puţin atâtea operaţii individuale câte cifre are cf[], fiecare constând în înmulţirea factorului f cu cifra curentă din cf[], cumularea transportului de la precedenta înmulţire la produsul găsit şi apoi separarea acestui produs în două părţi: cifra unităţilor (adică restul împărţirii produsului prin baza 10 de lucru) reprezintă tocmai cifra care trebuie înscrisă în cf[] pe rangul curent, iar partea rămasă după eliminarea cifrei unităţilor din produs (câtul împărţirii produsului prin baza de lucru) reprezintă transportul final, către următoarea operaţie individuală.
Să observăm că algoritmul acesta rămâne valabil şi dacă am folosi altă bază, în loc de baza 10 (probabil, vom avea nevoie mai departe de această observaţie şi nu o vom mai relua). Să observăm tot acum (va fi la fel şi în alte locuri) că în cf[] cifrele sunt înregistrate începând cu cifra unităţilor pe rangul 0 (în ordine inversă celeia cu care suntem obişnuiţi).
Timpul de calcul depinde şi de calculator şi de browser şi de diverse configurări asupra browserului; eu am obţinut 2-3 secunde pentru 1000!, 13-14 secunde pentru 2000! şi 94 secunde pentru 5000! - în ultimele două cazuri trebuind să fiu atent să clickez la vreme pe 'Continue' în fereastra:
'bignum' - modelare OOP în JS, folosind baza 10k (k = 6)
Este de aşteptat o creştere semnificativă de viteză, în cazul când am modela operaţiile folosind baza 106 (sau chiar şi de un ordin mai mic) în loc de baza 10. Sunt necesare funcţii de transformare între un şir de cifre zecimale şi un tablou numeric T[], în care fiecare element să corespundă unui anumit grup de maximum şase cifre zecimale consecutive din şir; este necesară o funcţie de înmulţire între numărul mare obţinut în T[] şi un număr natural obişnuit (factorul curent, în procesul calculării factorialului). Este un bun prilej de a prezenta o modalitate elementară de folosire în javascript a OOP—Object Oriented Programming, anume o modalitate similară cu OOP în C++ (dar de nivel elementar—de exemplu, fără derivare de clase şi chiar fără… clase). "Manualul de întrebuinţare" a obiectului nostru ar arăta cam aşa:
var Z = "112123123412345123456"; // un număr cu 21 de cifre zecimale var myBig = new bignum(Z); // construieşte folosind Z, obiectul 'myBig' // (conţinând T[] şi funcţiile indicate) alert(myBig.T); // T[] = [123456, 412345, 123123, 112] // T[0]=123456 reprezintă numeric grupul ultimelor 6 cifre din Z // ("cifra" unităţilor în baza 10^6) // T[3] = 112 este cifra cea mai semnificativă (în baza 10^6) alert(myBig.len); // 4 cifre în baza 10^6 (4 operaţii "cifră cu cifră") myBig.mul_int(90000); // T[] = T[] * 90000: alert(myBig.T); // [40000, 61111, 107111, 91081, 10], sau în forma zecimală: alert(myBig.to_str()); // "10 091081 107111 061111 040000" // (verificare: Z*9 şi adaugă 4 zerouri)
de observat că mai sus, T[3] = 91081 corespunde unui grup de 5 cifre zecimale, deci trebuie prefixat cu un '0' nesemnificativ - fiindcă prin construcţie, orice T[i] (exceptând doar cifra cea mai semnificativă, ultima din T[]) provine dintr-un grup de 6 cifre zecimale şi ca urmare, pentru conversia inversă: pentru fiecare k = 1..5, dacă T[i] < 10k atunci vor trebui adăugate (6 - k) zerouri nesemnificative.
Maniera de modelare OOP pe care o prezentăm aici (similar manierei elementare de lucru în C++) se poate folosi în general, pentru obiecte independente de DOM (care nu pretind modelarea şi a unor interacţiuni cu obiecte şi evenimente specifice Web).
/* Numai CIFRA trebuie modificat pentru a angaja altă bază; CIFRA=1 reduce totul la baza 10 */ var CIFRA = 6; // O cifră în baza 10000 (T[i]) conţine maxim // CIFRA cifre zecimale (din Z). var BAZA = eval("1e" + CIFRA); // Operaţiile "cifră cu cifră" (pe T[]) // angajează BAZA = 10 ^ CIFRA. /* "declaraţia" obiectului 'bignum' (descrierea conţinutului) */ function bignum( Z ) { // Z este un şir de cifre zecimale, în ordinea obişnuită, // pe baza căruia va fi construit obiectul (var myBig = new bignum(Z);) // variabile "de lucru" ("private" obiectului instanţiat) var len_Z = Z.length; // numărul de cifre zecimale din Z var rest = len_Z % CIFRA; // Numărul de cifre zecimale care rămân prin grupare // câte CIFRA, de la dreapta (cifra unităţilor) spre stânga. var len = 0; // Iniţializează numărul de elemente ale tabloului T[]. // Setează datele "membre" ale obiectului, accesibile prin operatorul de selecţie, "." this.T = new Array(); // Orice obiect păstrează un "pointer" la el însuşi, 'this' this.T[0] = 0; // Pe rangul 0 - cifra unităţilor (ultimele CIFRA cifre din Z) // converteşte la "integer" câte CIFRA cifre din Z şi înscrie în T[]: for( len = 0; CIFRA*(len + 1) <= len_Z; len++ ) { this.T[len] = parseInt(Z.substring(len_Z - CIFRA*(len + 1), len_Z - CIFRA*len), 10); } if( rest ) { // cifra "high" din T[], poate conţine mai puţin de CIFRA cifre zecimale this.T[len++] = parseInt( Z.substring( 0, rest ), 10 ); } this.len = len; // Setează ca dată "membru", numărul de valori înscrise în T[] // "metodele" de lucru asupra obiectului respectiv this.to_str = bignum_str; // forma zecimală corespunzătoare tabloului numeric T[] this.mul_int = bignum_mul_int; // înmulţeşte T[] propriu, cu numărul dat ca parametru // alte metode... (pentru adunare/înmulţire cu alt 'bignum', comparare, etc.) } /* urmează "implementarea" metodelor declarate în 'bignum' */ function bignum_str() { var th = this.len - 1; var str = "" + this.T[th]; // Cifrele cele mai semnificative (ultima valoare din T[]) while(--th >= 0) { // Valorile din T[] începând de la penultima spre stânga, var cifre = "" + this.T[th]; // trebuie transformate în şir de lungime CIFRA while(cifre.length < CIFRA) // prefixând eventual cu zerouri "nesemnificative" cifre = '0' + cifre; // cifre = " " + cifre; // separă grupurile de CIFRA cifre zecimale str += cifre; // Adaugă la 'str' grupul curent de CIFRA cifre zecimale } return str; } function bignum_mul_int( n ) { // Număr natural mai mic decât 2^53 / 10^CIFRA var i; var th = this.len; // <u>Prima trecere</u>: înmulţeşte numerele CIFRA din T[] cu n for( i = 0; i < th; i++ ) this.T[i] *= n; // A doua trecere: corectează în raport cu BAZA (la prima trecere puteau rezulta // în T[i] şi valori mai mari decât BAZA; le reduce modulo BAZA şi propagă transportul) for( i = 0; i < th - 1; i++ ) { if( this.T[i] >= BAZA ) { n = Math.floor( this.T[i] / BAZA ); // Refoloseşte variabila n din apel this.T[i] = this.T[i] % BAZA; this.T[i+1] += n; // Propagă transportul spre dreapta (la rangul i+1) } } while( this.T[ th - 1 ] >= BAZA ) { // Reduce şi ultima cifră, extinzând eventual T[], this.T[ th ] = Math.floor( this.T[ th - 1 ]/BAZA ); // cu transportul generat. this.T[ th - 1 ] %= BAZA; this.len++; // Corectează şi numărul de elemente CIFRA existente în T[] th++; // reia "reducerea" şi pentru ultima cifră adăugată } return this; // returnează un "pointer" la obiect, util pentru formulările recursive şi // pentru imbricări ca alert( myBig.mul_int(n).to_str() ) }
Pentru bignum_mul_int(n) am folosit un algoritm de înmulţire "cu două treceri" (v. şi [2]); posibilitatea acestui algoritm decurge din faptul că orice valoare T[i] (număr mai mic decât 106, conform cu definiţia 'bignum') ar deveni prin înmulţire cu numărul n o valoare care poate fi înregistrată şi ea în T[i] ("încape", fără trunchiere şi fără erori de rotunjire).
Mai precis, javascript îşi reprezintă numerele (indiferent că sunt sau nu întregi) în formatul IEEE_754—double precision floating point, pe 64 biţi; în cazul unui număr întreg, sunt reprezentate exact numai cele mai semnificative 15-16 cifre zecimale, anume pe 53 de biţi din cei 64 (iar restul biţilor reprezintă numărul de cifre care urmează în număr). Fiindcă 253 ≈ 9007*1012, iar max(T[i]) = 106 - 1, rezultă că factorul maxim n pentru care produsul cu T[i] nu depăşeşte "capacitatea" lui T[i] este (împărţind prima valoare menţionată prin cea de-a doua) 9.007.208.261 - un număr suficient de mare, ca să nu apară "depăşiri" în cazul problemei factorialelor (doar dacă ar vrea careva să calculeze factorialul unui număr de 10 cifre, ceea ce ar fi o absurditate fără nici o şansă de acoperire).
Rezultă de aici că baza poate fi încă mărită, fără a apărea probleme de depăşire; dar dacă ea s-ar mări dincolo de 1012, atunci raportul menţionat mai sus va deveni mai mic de 90.071, adică deja nu vom mai putea calcula (în felul descris mai sus, cu două treceri) factorialul lui 100.000 (ceea ce n-ar fi chiar absurd, de calculat… totuşi, nu în javascript! care nu pentru calcul numeric a fost creat).
Calculul factorialelor, angajând un obiect 'bignum'
Acum putem folosi 'bignum' pentru a calcula factorialele, de exemplu prin următoarea funcţie (de calcul iterativ):
function big_fact( n ) { var big = new bignum("1"); for(var f = 2; f <= n; f++) big.mul_int( f ); return big.to_str(); }
De data aceasta, 1000! rezultă în mai puţin de o secundă, 2000! în 3-4 secunde, iar 5000! rezultă în 33 secunde - timpi cam de trei ori mai buni, decât în cazul bazei 10. Între cele două programe redate mai sus, există şi o deosebire importantă privind desfăşurarea calculului: primul (în baza 10) făcea calculul în cadrul unei singure funcţii (deci în cel mai economicos mod), pe când al doilea implica apelarea repetată a unei funcţii, consumând astfel timp nu numai pentru calculul necesar, dar şi pentru a îndeplini protocoalele de apel respective (transmite parametrii necesari serviciului apelat, salvează şi apoi recuperează punctul de revenire, etc.). Al doilea program, deşi dezavantajat faţă de primul prin faptul că a trebuit să apeleze repetat la funcţia 'mul_int', a dat totuşi timpi mai buni - ceea ce întăreşte concluzia că modelarea calculelor folosind baza 106 este mult mai eficientă decât modelarea obişnuită, în baza 10.
În fine, versiunea recursivă (aceasta ne propusesem să redăm în diverse limbaje) se poate formula astfel:
function big_fact_rec(big, n) { // 'big' referă un "bignum" iniţial if(n == 1) return big; return big_fact_rec(big.mul_int(n), n-1); // Reapelează pentru 'big'-ul rezultat } // după înmulţire cu factorul curent // Un exemplu de folosire: // document.write( big_fact_rec( new bignum("1"), 1000).to_str("") );
Pentru un număr mai mare ca 1000 (în funcţie şi de browser) rezultă eroarea too much recursion sau "Out of Memory" (fiindcă javascript are stabilită limita de 1000 de apeluri recursive). Dacă am vrea să calculăm în această manieră şi 1500! de exemplu, atunci am putea modifica "condiţia de oprire" (n == 1) astfel:
var stop = 1; // "coborâre" până la n == stop (cu 'stop' setat în prealabil) function big_fact_rec(big, n) { // 'big' referă un "bignum" obţinut anterior if(n == stop) return big; // "revenirile" încep când n coboară la 'stop' return big_fact_rec(big.mul_int(n), n-1); // calculează n*(n-1)*...*stop. } /* Aplicaţie: obţine întâi 500!, apoi pe baza lui rezulta şi 1500! */ var myBig = big_fact_rec(new bignum("1"), 500); // obţine 500! în myBig stop = 500; // schimbă condiţia de oprire (evită "too much recursion") document.write( big_fact_rec( myBig, 1500 ).to_str() ); // în myBig se obţine 1500! /* Aplicaţie: obţine un produs de numere consecutive */ stop = 500; document.write( big_fact_rec( new bignum("1"), 1000).to_str() ); // 500*501*...*1000
4) Python
În python (opera lui Guido van Rossum, 1990), gruparea instrucţiunilor este dată de indentare (nu de "begin" şi "end" ca în Pascal şi nici de acolade ca în C, în perl, în PHP, etc.) şi nu sunt necesare declaraţii de variabile sau de argumente. Python poate opera ca un shell ("interpretor de comenzi"): dacă este apelat de la consolă (vb@debian:~/lar$ python) atunci afişează un "prompt" şi aşteaptă tastarea unei comenzi, pe care o citeşte şi (dacă este una corectă) o execută, după care din nou afişează promptul; dacă este apelat împreună cu un nume de fişier drept argument (vb@debian:~/lar$ python fact.py), atunci citeşte şi execută scriptul din acel fişier (sub Linux, trebuie ca în prealabil fişierul respectiv să fie făcut "executabil": chmod +x fact.py).
În Python, întregii sunt la fel ca longint din C; dar, dacă ei sunt implicaţi în operaţii (cu întregi) prin care ar depăşi limita specifică tipului longint, atunci ei sunt "convertiţi" în mod automat la tipul propriu Long, care poate păstra numere întregi de orice lungime.
import sys, textwrap # încorporează în program modulele necesare # (analog, "#include..." în C, sau "use ..." în perl) def factorial( n ): # returnează factorialul lui n (de fapt, returnează # un "pointer" la valoarea de tip Long respectivă) if n == 1: return 1 return n * factorial( n - 1 ) sys.setrecursionlimit(11000) # măreşte stiva interpretorului # (permite calculul recursiv de 10000!) fo = open("factoriale-py.txt", 'a') # pentru 'append' în fişierul indicat for n in range(1000, 10001, 1000): # Calculează 1000!, 2000!, ..., 10000! # şi scrie în 'fo' (linii de maxim 80 cifre) fact = factorial( n ) fo.write(str(n) + "! =\n" + textwrap.fill( str(fact), width = 80 ) + "\n\n")
Rezultatul 'factoriale-py.txt' se obţine într-un timp remarcabil - sub 1 minut - şi măsoară 2345 rânduri de câte (maximum) 80 de caractere (desigur, numărând şi cele 10 linii informative "1000!=" etc., precum şi cele 11 rânduri albe care separă valorile).
Dar programul nostru nu se străduieşte deloc cu inteligenţa: după ce obţine şi scrie în fişier valoarea 1000!, apelează factorial() pentru a calcula 2000!; iar calculul o ia de la capăt 1*2*3* ... *1000*1001*1002* ... *2000, obţinând şi 2000! care este şi el scris în fişier; apoi se apelează iar factorial(), calculând 1*2*3* ... *1000*1001* ... *2000*2001*2002* ... *3000, obţinând şi 3000!; ş.a.m.d. Logica aceasta este evident defectuoasă; o modalitate de îndreptare (arătată şi într-un alt program mai sus) se bazează pe implicarea unei "condiţii de oprire" variabile:
import sys, textwrap stop = 1 # "coborârea" se face până la n == stop def factorial( n ): if n == stop: return stop return n * factorial(n - 1) # produsul n*(n-1)*...*stop sys.setrecursionlimit( 11000 ) fo = open("fact-stop-py.txt", 'a') fach = 1 # păstrează valoarea 'fact' curent for n in range(1000, 10001, 1000): fact = fach * factorial( n ) # Înmulţeşte 'fact' anterior găsit # cu numărul returnat de factorial(). fach = fact # salvează 'fact'-orialul curent obţinut stop = n + 1 # setează noul 'stop' pentru reapelarea factorial() fo.write(str(n) + "!= \n" + textwrap.fill(str(fact), width = 80) + "\n\n")
Se evită astfel, repetarea aceloraşi calcule; 1000! este calculat o singură dată, după care valoarea respectivă este înmulţită cu 1001 * 1002 * ... * 2000 obţinând 2000!, ş.a.m.d. Se fac mai puţine operaţii, numai că de data aceasta (pe versiunea reprodusă aici - cu siguranţă ea se poate îmbunăţăţi considerabil) au loc nişte înmulţiri de numere ambele mari (în timp ce în varianta precedentă, se înmulţea mereu un număr mare cu un factor mic) - încât nu rezultă nicidecum un timp mai bun (în cazul versiunii brute, date aici).
5) perl
perl (creaţia lui Larry Wall, 1987) permite reutilizarea chiar şi de componente software care sunt "scrise" într-un alt limbaj. Un exemplu potrivit în contextul nostru este acesta: GMP—GNU Multiple-Precision este o bibliotecă realizată în C (şi limbaj de asamblare) pentru domeniul aritmeticii cu numere mari ("bignum arithmetic"), iar modulul perl Math::BigInt permite conectarea şi folosirea din programe perl a bibliotecii GMP. Astfel că putem obţine de exemplu 10000!, fără a scrie vreun program:
vb@debian:~/lar$ \ > perl -MMath::BigInt -e 'print Math::BigInt->new(10000)->bfac();' > fact-line.txt
De pe linia de comandă a shell-ului s-a invocat interpretorul perl, furnizându-i prin opţiunea -M numele modulului necesar şi precizând sub opţiunea -e comanda care trebuie executată, constând în: apelarea funcţiei-constructor Math::BigInt->new() pentru a obţine un "bignum" corespunzător parametrului 10000 furnizat; apoi, pentru obiectul "bignum" obţinut, se apelează metoda sa bfact() care calculează şi injectează în obiectul respectiv valoarea 10000!; apoi, rezultatul respectiv este scris prin "print" şi operatorul de redirectare ">", în fişierul 'fact-line.txt'.
Rezultatul se obţine nemaipomenit de repede (5 secunde?). Dar pentru 20000! rezultatul (care are 77338 cifre şi începe memorabil: 18 19 20) se obţine într-un timp mult prea mare (un minut?) ca să poată fi vorba de apelarea bibliotecii GMP! În documentaţia de la Math::BigInt se precizează că API (Application Programming Interface, "logica internă") nu depinde de care bibliotecă "bignum" se foloseşte; este prevăzut un parametru de configurare lib cu valoarea implicită "Math::BigInt::Calc", încât dacă nu se precizează altfel, atunci nu GMP se foloseşte, ci Math::BigInt::Calc - care doar emulează în perl biblioteca GMP (şi evident, viteza are de suferit).
Următoarea variantă a programului (There's more than one way to do it este motto-ul limbajului perl) impune să se folosească GMP şi prevede o anumită formatare a scrierii într-un fişier a rezultatului.
#!/usr/bin/perl # indică shell-ului care "actor" trebuie să interpreteze acest script use Text::Autoformat qw(autoformat break_at); # pentru formatare (câte caractere pe rând, marcarea sfârşitului de rând, etc.) use Math::BigInt lib => 'GMP'; # expliciteză biblioteca "bignum" care trebuie folosită (GMP) # în mod implicit, lib referă Math::BigInt::Calc (emulator perl de GMP) my $i = $ARGV[0]; # preia din linia de comandă numărul al cărui factorial trebuie calculat open(FH, ">", "factGMP.txt"); # creează şi/sau deschide pentru scriere fişierul 'factGMP/txt' print FH $i . "! = \n"; # scrie în fişier, pe prima linie, "$i! =" (de exemplu, "100000! =") my $fac = Math::BigInt->new($i)->bfac()->bstr(); # bfac() şi bstr() sunt metode ale obiectului creat prin new() # bfac() conectează GMP mpz_fac_ui(mpz_t, unsigned long) - calculează factorialul; # bstr() returnează valoarea ca şir (preluat în final în variabila $fac) my $format = autoformat $fac, {left => 1, right=>80, break=>break_at('')}; # rânduri de lungime 80 print FH $format, $i."! are ".length($fac)." cifre zecimale.\n"; # scrie factorialul şi lungimea lui (numărul de cifre)
Programul se lansează desigur, prin "vb@debian:~/lar$ ./perl-fact.pl 100000" (după ce în prealabil, s-a fixat "drept de execuţie" pe fişier, prin chmod +x perl-fact.pl). Acum se foloseşte GMP, iar diferenţa faţă de prima versiune (când se folosea M::B::Calc) este enormă: am obţinut 100000! în 30 secunde (are 456574 cifre, aproape 452 KB).
Foarte bine, GMP este cea mai bună bibliotecă "bignum" şi am văzut mai sus ce simplu o putem folosi din perl (ea se poate folosi şi din programe PHP, sau C, Python, etc.)… Rămâne însă de realizat şi ceea ce ne-am propus la început - voiam să prezentăm modalităţi de lucru în diverse limbaje, folosind ca pretext calculul recursiv al factorialelor…
Observaţie. "Operaţii cu numere mari" nu-i un simplu "moft" teoretic; pe CPAN există numeroase module care folosesc Math::BigInt în diverse scopuri: verificare de adrese IP, criptografie, autentificare, etc. (Net::IP, Crypt::PBC, DateTime::Util::Calc, Authen::Bitcard, etc.).
Vom adapta chiar obiectul "bignum" pe care l-am modelat mai sus pentru javascript. Definim clasa de obiecte necesară într-un fişier Bignum.pm (".pm" de la "perl module"), urmând să includem acest fişier ("use Bignum") în programul ".pl" în care am avea nevoie de obiectele respective. Un package defineşte un set de tabele de simboluri pentru a înregistra variabilele proprii, funcţiile, etc. (analog cu folder, sau director; pot exista fişiere cu acelaşi nume - respectiv, variabile sau funcţii cu acelaşi identificator - dacă ele sunt în foldere diferite - respectiv în "pachete" diferite). Dezvoltăm pe bucăţi, cum se face în practică: scrii o bucată, o testezi, o pui la punct şi apoi treci la altă bucată… (Grigore Moisil a dat o interpretare mai umană aceastei reguli: "fiecare OM are dreptul la un pahar; dar după aceea devine alt OM.") Când va fi invocat constructorul - de exemplu prin Aici, obiectul "bless"-ed este o referinţă la tabloul inversat (prin reverse) al valorilor "longint" rezultate prin acţiunea unpack asupra şirului În perl, un tablou obişnuit se poate defini folosind sigiliul @, de exemplu my @arr = ( 11, 3.25, 'abcd' ); defineşte tabloul denumit 'arr', cu trei elemente; acestea pot fi de orice "tip", încât "tablou" în perl înseamnă mai degrabă, listă de variabile sau valori; ele pot fi accesate folosind indexarea obişnuită, numai că (tocmai fiindcă pot fi de orice "tip") ele sunt în fond nişte variabile independente grupate împreună în @arr - şi fiindcă sigiliul de variabilă este Tablourile apar în trei-patru tipuri importante, de expresii: 1. my @clone = @arr; 2. my 3. my 4. my În "bucata" de mai sus, ceea ce este "bless"-ed prin ultima instrucţiune - este o referinţă la tabloul returnat de 'unpack' (primul număr se va obţine prin Extindem Bignum.pm, adăugând subrutine similare celor de la §3) javascript, pentru înmulţire cu un număr obişnuit şi pentru conversie la forma zecimală (minimul necesar, pentru a putea formula un program de calcul al factorialelor). Putem verifica iarăşi printr-un "one-liner": S-a obţinut adresa de memorie corespunzătoare referinţei (de "tip" SCALAR) returnate de to_string; pentru a obţine valoarea referită, trebuie să dereferenţiem: Bineînţeles că am preferat returnarea de referinţe şi nu de valori; a returna un tablou de exemplu (în loc de o referinţă la el), înseamnă implicit a face o copie suplimentară într-o altă zonă, a acelui tablou. De obicei însă, pentru testare şi pentru "punerea la punct" (nu numai ca "logică", dar şi pentru analiza şi reconsiderarea structurării datelor) se folosesc module specializate; iată un mic program de investigare tipic, folosind Data::Dumper: $VAR1 indică un obiect bless-ed de către modulul 'Bignum'; ca memorie, acest obiect nu este altceva decât o referinţă (este redat cu "[ ]") la o listă de 4 valori; aceste valori apar ca fiind şiruri, dar numai pentru faptul că Dumper s-a ocupat de serializarea valorilor numerice din tabloul respectiv; recunoaştem în valorile respective, grupurile de câte 6 cifre, de la dreapta spre stânga, din şirul de cifre zecimale transmis constructorului. Funcţia factorial are două argumente, cum se vede în linia 9; primul este o referinţă la un obiect Bignum (iniţial, în linia 9 - cel creat pentru numărul 1), iar al doilea este numărul căruia trebuie să-i determine factorialul. Definiţia funcţiei factorial (liniile 8 - 10) foloseşte variabila perl $_ pentru a adresa argumentele şi foloseşte operatorul condiţional ? (analog celui din C) pentru a discerne între cele două ramuri de execuţie ("oprire" dacă factorul $_[1] a coborât până la 1, respectiv reapelare). Presupunând programul de mai sus (desigur, fără numerele de linie!) în fişierul "big-fac.pl" (cu "drept de execuţie" setat prin chmod), el va putea fi invocat din linia de comandă a shell-ului prin big-fac.pl 10000 pentru a obţine 10000! Rezultatul va fi scris în fişierul "bigfac.txt"; Fişierul este deschis prin linia 12, pentru adăugare (şablonul ">>", la fel ca în sistemele de operare Linux, DOS); scrierea în fişier a rezultatului se face folosind Text::Autoformat (folosit şi într-un alt program, mai sus), cu formatarea asigurată prin linia 17; după încheierea scrierii valorii respective, se adaugă în fişier un separator faţă de viitoarea valoare adăugată, constând într-o linie de 80 de caractere "-" (vezi şablonul ' "-" x 80 ' în linia 20; "x" este un operator de repetiţie). Timpul de execuţie interesează doar pentru comparaţii (altfel, este specific fiecărui calculator); am obţinut 1000! în 1 secundă, 5000! în 13 secunde, 10000! în 54 secunde - mult inferior rezultatelor obţinute cu Math::BigInt lib => 'GMP' (vezi mai sus); dar este normal să fie aşa: în GMP algoritmii de calcul sunt dintre cei mai performanţi (aici am folosit doar înmulţirea elementară, doar că într-o bază mai mare), sunt minuţios optimizaţi, implementaţi eficient (cu bucăţi în limbaj de asamblare optim) şi în plus, în GMP nu se foloseşte recursivitatea. Ne ocupăm întâi de un program C bazat pe biblioteca GMP; aceasta va trebui să fie compilată şi instalată; GMP face parte din proiectul GNU, încât vom prezenta pe scurt istoria corespunzătoare. Apoi, vom modela în C++ un class "bignum", pentru un program independent de calcul al factorialelor; de data aceasta nu vom mai folosi baza 10k precum în cazurile precedente, ci baza 2k, k = 16 (= GMP—GNU Multiple-Precision a fost lansată în 1991; se poate folosi cam pe orice platformă (Linux, Windows, MacOS, etc.), indiferent de tipul de CPU (dar codul produs include optimizări specifice diverselor microprocesoare, de exemplu pentru familia "x86") şi cu diverse compilatoare de C sau C++ (dar este preferat totuşi, gcc). Pentru a putea folosi biblioteca GMP într-un program C, trebuie întâi să obţinem sursele respective şi să le compilăm pe propriul sistem. Se download-ează arhiva corespunzătoare de la GMP şi se dezarhivează, rezultând un director "gmp-4.2.1" care conţine toate sursele bibliotecii; rămâne ca acestea să fie compilate - folosim pentru aceasta, compilatorul GCC. În 1983 Richard Stallman a lansat proiectul GNU, cu intenţia de a dezvolta "a sufficient body of free software"; GNU este un acronim pentru "GNU's Not Unix" (UNIX® este un sistem de operare "not free", dezvoltat din 1969 împreună cu limbajul C, la Bell Laboratories). "Free software" cuprinde produsele software pentru care licenţa aferentă (documentul care dă dreptul de a folosi produsul) nu impune nimănui costuri monetare pentru folosire; licenţa statuează că produsul poate fi utilizat liber, pe oricâte calculatoare se doreşte; sursele sunt distribuite gratuit în scopuri de studiere, modificare, extindere şi redistribuire în forma originală sau modificată. Astăzi, cele mai cunoscute exemple de "free software" sunt sistemul de operare Linux şi browser-ul Firefox. În cadrul proiectului GNU, Linus Torvalds a lansat în 1991 proiectul Linux (iniţial, cu vreo 10000 linii de cod), pentru a realiza un sistem de operare free care să poată substitui sistemul Unix; Linux a ajuns în 2003 la "Linux 2.6.0", cu aproape 6 milioane de linii de cod; s-au făcut estimări ale costului de producere a Linux-ului într-un cadru de dezvoltare obişnuit, comercial-privat (câţi programatori performanţi sunt necesari, câte luni de muncă, ce salarii trebuie achitate, etc.): re-crearea Linux-ului ar costa măcar 600 Mega €. Linux a fost scris folosind limbajul C suportat de compilatorul GCC şi limbaj de asamblare (cu sintaxa specifică GCC). GCC GNU Compiler Collection (proiect iniţial în 1985, de către Richard Stallman) este un set de compilatoare pentru diverse limbaje de programare (C, C++, Java, Ada, Fortran şi altele). GCC a fost portat (modificat ca să ruleze) pe mai multe platforme decât oricare alt compilator existent; GCC este compilatorul folosit pentru crearea limbajelor perl, Python, etc. şi de asemenea, pentru dezvoltarea unor sisteme de operare (FreeBSD, BeOS, etc.). GCC face parte din sistemul Linux (este instalat automat), fiind compilatorul oficial pentru GNU. După 1995, s-au creat diverse "instrumente" care permit folosirea unor componente GNU (între care şi GCC) pe sisteme Windows: Cygwin ("Linux-like environment for Windows"), MinGW Minimalist GNU for Windows, DJGPP, etc. Compilarea surselor GMP obţinute în directorul "gmp-4.2.1", pe un sistem Linux, folosind compilatorul GCC - este asigurată în mod standard (valabil în general, pentru oricare altă bibliotecă cu surse în C) prin următoarele 4-5 comenzi: Ultima comandă instalează pe sistem fişierul "obiect" rezultat în urma compilării; desigur, "instalarea" nu o poate face decât "superuserul" root - de aceea "make install" a fost prefixată de comanda Folosind un editor de text obişnuit, scriem următorul program C şi salvăm ca "factorial.c": Pentru a obţine fişierul executabil corespunzător, să-i zicem "fact-gmp", folosim: Opţiunea Programul va putea fi executat folosind (de exemplu pentru a obţine 100!): mpz_t desemnează o struct-ură cu trei câmpuri de date: numărul de ' mpz_fac_ui() (linia 9) primeşte un pointer mpz_ptr ("factorial", în program) la un "corp" de tip mpz_t şi un număr (şi va determina modificarea "corpului" vizat, încât să conţină factorialul numărului indicat). Trebuie precizat în final, că viteza cu care se obţin factorialele este chiar uluitoare; 100000! se obţine aproape instantaneu. Evident, meritul nu este al programului de mai sus, fiindcă el nu face altceva decât să invoce g++ (sau "c++", pe unele sisteme) este compilatorul pentru C++ din GCC. Numele fişierelor "header" specifice C++ nu au extensia ".h" (sau ".hh") obişnuită în C (în /usr/include/c++/4.2.1/ apare fişierul "fstream" şi nu "fstream.h"). Ca şi "package" în perl, "namespace" defineşte un spaţiu de valabilitate pentru nume; aşa cum în perl, după "use Bignum" puteam folosi în program elementele definite în modulul Bignum.pm, tot aşa "Bignum" nu mai poate fi modelată în maniera folosită la javascript şi la perl (cel puţin, nu într-un mod natural); mai precis, nu mai putem miza pe operare în baza 106, pentru că (spre deosebire de perl, etc.) C prevede specificaţii exacte pentru numere. Numărul 999999 (cifră în baza 106) este de tip unsigned long (32 de biţi, valori 0..232-1), dar pătratul acestui număr (valoare care "încăpea" într-o variabilă obişnuită, în cazul javascript sau perl, putând separa apoi restul faţă de 106 şi respectiv, transportul) depăşeşte capacitatea de 32 de biţi (iar depăşirea este reflectată numai de bitul "Carry" din registrul de "flaguri" al microprocesorului, adică ar trebui să implicăm şi limbaj de asamblare, ca să furnizăm transportul). Am putea folosi doar baza 104 (în loc de 106); este preferabil în acest caz, să folosim ca bază capacitatea maximă a unui registru de 16 biţi (0..216-1). Următoarele două programe experimentează asupra ideilor de lucru specifice utilizării acestei baze. Fiindcă short int are jumătate din dimensiunea unui long, vom putea considera pentru factorial un tablou cu elemente de tip unsigned short int, urmând să folosim o variabilă temporară de tip unsigned long pentru produsul dintre cifra curentă a acestui tablou şi factorul curent (tot de tip unsigned short int) - valoare care va trebui apoi separată în părţile "Low" şi "High". Clasa "Bigfac" - denumirea "Bignum" folosită mai sus este de fapt nepotrivită: n-am modelat operaţii "bignum" decât în sensul strict necesar calculării de factoriale - trebuie să prevadă (ca dată privată) un tablou de short int care să reprezinte factorialul şi trebuie să ofere acces public la o metodă de înmulţire (a tabloului, cu factorul furnizat din afară). Desigur, rezultatul înmulţirii (care nu este neapărat cel final - valoarea factorialului) se obţine în tabloul intern de "short int"-uri, reprezentat deci în baza de lucru 2^16; numai rezultatul final va trebui returnat sau scris într-un fişier. Rezultatul final poate fi afişat imediat în hexazecimal (prefixând afişarea prin "cout<<hex;"), încât nu este necesar ca "Bigfac" să mai cuprindă şi vreo funcţie de conversie! Pentru a furniza totuşi rezultatul în forma obişnuită, el trebuie convertit la baza 10; dar este mai eficient (cam de 4 ori!) să convertim la baza 104 ("conversia" mai departe la baza 10, fiind apoi banală). Descriem clasa "Bigfac" în fişierul bigfac.h: Fie de exemplu, dword DW = 0xA111B222 o valoare dată în hexazecimal (cu prefixul "0x"); DW are 8 cifre hexazecimale (32 de biţi); în memoria internă, DW este reprezentat pe două "word"-uri de adrese consecutive şi apar două posibilităţi: la adresa mai mică 0xA111 (cuvântul "high" din DW), iar la adresa următoare 0xB222 (cuvântul "low") şi respectiv invers: cuvântul "low" la adresa inferioară, iar cel "high" la adresa următoare. Dar trebuie să fie clar, "reprezentarea în memoria internă" nu este vreun atribut al "memoriei" ca atare, ci este un atribut specific microprocesorului care gestionează memoria respectivă; microprocesoarele Intel x86 reprezintă partea "low" la adresa mai mică (formatul "little-endian" - ca şi cum numărul s-ar scrie "de la dreapta spre stânga", începând cu cifra unităţilor), în timp ce altele (microprocesoarele "Motorola", de exemplu) folosesc formatul "big-endian" (acesta ar corespunde ordinii obişnuite de scriere a numărului). Macrourile definite mai sus funcţionează "pas cu pas" astfel: LOW(DW) = (word) 0xA111B222 & 0xFFFF = (word) 0xA111B222 & 0x0000FFFF (s-a convertit al doilea operand la tipul mai lung al primului) = (word) 0x0000B222 (s-a efectuat operaţia AND pe biţii operanzilor) = 0xB222 (s-a efectuat conversia de tip, la word). Desigur, în cazul "big-endian" am fi obţinut ca rezultat 0xA111. Iar HIW(DW) = (word) 0xA111B222 >> 16 & 0xFFFF = (word) 0x0000A111 & 0xFFFF (primul operand a fost deplasat spre dreapta cu 16 poziţii binare) = ... = 0xA111. Metodele clasei "Bigfac", declarate mai sus, sunt definite în fişierul bigfac.cc următor: Pentru a compila şi lega împreună cele trei fişiere, apoi pentru execuţie şi afişare - putem folosi: Privind timpul de execuţie, avem întâi de observat că nu putem proba pentru n = 100000: în constructorul Bignum(N) s-a prevăzut tipul long pentru parametrul de intrare N (astfel că putem considera şi N=100000), dar în funcţia tw_mul_w(K) pentru K s-a "prevăzut" doar word (încât nu se va putea calcula produsul cu un factor mai mare de 65535).
Pentru 10000! rezultatul este imediat (o secundă?). Calculând pentru n=65000 (care este de tip word), am obţinut rezultatul (corect) în aproape un minut; dar apoi, păstrând din codul metodei " În sfârşit, vrem să exprimăm şi programul de calcul recursiv al factorialelor (cum ne propusesem iniţial, pentru diversele limbaje). Însă pentru a permite formulări recursive, modelul respectiv (aici, "bigfac.h") trebuie în general, să îndeplinească o condiţie - asupra căreia am mai atras atenţia: metoda bignum_mul_int() a obiectului "bignum" din §3) javascript "returnează un pointer la obiect, util pentru formulările recursive".
Desigur, am modificat puţin şi definiţia operatorului "<<" din "bigfac.cc", pentru a obţine afişarea redată aici. 100! are deci 33*4 = 132 de cifre hexazecimale; numărul de cifre zecimale este cuprins între 39*4+1 = 157 şi 40*4 = 160, după cum cifra cea mai semnificativă în baza 10^4 este '9', sau '93', sau '933', respectiv '9332' (despărţind cumva, şirul afişat în grupuri de câte 4 cifre, se vede că ultimul grup este "incomplet", cu numai două cifre - adică sunt 39*4+2 = 158 de cifre zecimale). Rezultatul 10000! (cu 7404*4 cifre hexazecimale, respectiv 8915 cifre în baza 10^4) se obţine şi el, aproape instantaneu (o secundă?). Am indicat însă, două variante pentru alocarea obiectului de memorie "fac": global (în segmentul de date repartizat programului) şi - în linia "comentată" - local (în segmentul de stivă). Instrucţiunile de acces la memorie au setată drept sursă/destinaţie implicită segmentul DS ("Data Segment", prin care se adresează la nivelul microprocesorului, datele "globale") - astfel că, în principiu există o diferenţă de viteză între a accesa date globale şi respectiv, "locale", diferenţă care este mai mare sau mai mică în funcţie de frecvenţa accesării datelor respective; din acest motiv s-a ajuns la ideea includerii în microprocesor a unei memorii cache şi a unei unităţi de încărcare anticipată a instrucţiunilor şi a datelor (în loc să acceseze memoria principală, prin intermediul magistralelor de legătură, microprocesorul ia datele respective direct din "cache"-ul intern şi cu cât "cache-size" este mai mare, cu atât se diminuează diferenţa menţionată). Observaţie. Limbajul C modelează (mai îndeaproape sau mai transparent, decât alte limbaje) un microprocesor standard (iar compilatoarele de C prevăd optimizări specifice diverselor microprocesoare particulare) - încât învăţarea limbajului C trebuie agrementată şi cu ideile generale (nu neapărat în amănunt, sau riguros) pe care se bazează structura şi funcţionarea unui microprocesor… În limbaj de asamblare, programul ar avea cam 200 de rânduri - adică în privinţa lungimii textului-sursă, ar fi de câteva ori mai "lung" decât în oricare dintre limbajele de nivel înalt. Însă în realitate, dimensiunea unui program nu se măsoară prin numărul de rânduri; "executabilul" ar fi (cu totul) cam de 3 Ko - adică de multe ori mai "scurt", decât rezultatul obţinut prin compilarea unei surse dintr-un limbaj de nivel înalt. În [2] avem un program TASM (Turbo Assembler) pentru calculul factorialelor, folosind "real mode", cu segmente de cod "use16". Acum vom folosi asamblorul GNU as (numit şi GAS), linker-ul GNU ld (ambele incluse în colecţia de instrumente de programare GNU Binary Utilities) şi utilitarul GNU make (care permite întreţinerea unui grup de programe interdependente). Vrem să obţinem un program executabil amifac, care la apelarea din linia de comandă a shell-ului prin ./amifac N (de exemplu, ./amifac 10000) să determine N! (factorialul numărului N) şi să scrie rezultatul sub forma uzuală la ieşirea standard (pentru scrierea într-un fişier "fact.10000" se va putea folosi redirectarea: ./amifac 10000 > fact.10000). Pentru transmiterea parametrilor şi pentru asigurarea revenirii după terminarea execuţiei, shell-ul asociază programului apelat următorul cadru stivă: N este transmis ca pointer la un şir ASCII-Z; deci avem nevoie întâi de o subrutină care să furnizeze valoarea numerică a lui N (în C am avea funcţia atoi()). Această subrutină trebuie să preia pointerul la şir de la (ESP + 8), să parcurgă şirul cifrelor (până la '\0') şi să constituie valoarea "unsigned long" corespunzătoare; vom scrie această subrutină în fişierul edi_toi.s. Va trebui apoi să alocăm memorie pentru cifrele factorialului. Vom reprezenta factorialul în baza 2^16 (produsul a două cifre 2^16 ocupă 32 de biţi); cum am arătat la începutul articolului, necesarul de memorie rezultă plecând de la valoarea lg(N!). Tot folosind lg() se va putea determina şi necesarul de memorie pentru conversia factorialului de la baza 2^16 la baza 10^4. Cele două subrutine de calcul vor folosi desigur instrucţiuni FPU (ale coprocesorului) şi vor fi scrise în fişierul lg_fac.s. Pentru alocarea memoriei folosim apelul de sistem mmap() (în C am folosi funcţia malloc(), care foloseşte şi ea fie apelul de sistem brk(), fie mmap() după anumite calcule de dimensiune asupra zonelor de memorie existente); mmap() asigură (sub Unix) maparea unui fişier (eventual, anonim) pe o zonă de memorie virtuală (legătura dintre memoria virtuală alocată şi memoria reală fiind apoi asigurată de unitatea de gestiune a memoriei încorporată în microprocesor). Fiindcă avem de făcut două alocări de zone, iar mmap() aşteaptă 6 parametri (transmişi în stivă), vom scrie subrutina respectivă într-un fişier separat, alloc_mem.s. În fişierul amifac.s vom scrie programul "principal"; acesta va apela subrutina din edi_toi pentru a obţine N, apoi va apela prima subrutină din lg_fac pentru a obţine o estimare a numărului de cifre-2^16 ale factorialului şi apoi, va apela alloc_mem; urmează să se calculeze cifrele-2^16 ale factorialului, în zona alocată. După obţinerea factorialului în baza 2^16, se apelează a doua subrutină din lg_fac pentru a obţine o estimare a numărului de cifre-10^4 ale factorialului, apoi se apelează alloc_mem pentru alocarea corespunzătoare şi urmează calculele de conversie de la forma 2^16 găsită, la forma 10^4. Vor fi necesare multe modificări, pe parcursul lucrului (trasarea execuţiei folosind de exemplu debugger-ul GNU gdb, pentru a sesiza greşeli, posibile corecturi sau optimizări; re-asamblări, re-link-uri, etc.). Mai ales că am împărţit programul în mai multe fişiere, pentru a evita să tastăm mereu comenzile necesare pentru asamblare (as <opţiuni> amifac.s, etc.) şi pentru link-are (ld <opţiuni> amifac.o etc.o) putem folosi make; în acest scop, creem un fişier Makefile în care specificăm (conform unei sintaxe simple, asumate de make) comenzile care trebuie executate în situaţia modificării vreunuia dintre fişierele programului: După orice modificare a unuia sau altuia dintre fişierele programului, simpla comandă make va determina execuţia comenzilor din fişierul Makefile, recreând executabilul amifac (sau producând mesaje de eroare, în cazul existenţei unor greşeli de sintaxă). Pentru determinarea valorii numerice a unui şir de cifre zecimale se foloseşte (în mod standard) schema lui Horner. De exemplu, fie şirul "4567" (el este reprezentat ASCII-Z prin secvenţa de 5 octeţi 0x34,0x35,0x36,0x37,0x0 (codul ASCII pentru "0" fiind 0x30)); obţinem valoarea numerică N modelând calculul N = ((4*10 + 5)*10 + 6)*10 + 7 (iniţial N=0; apoi, N = N*10 + cifra_curentă, repetat până când cifra_curentă==0x0, unde cifra_curentă = cod-ASCII - 0x30). În [1], [2] avem subrutine TASM pentru a obţine forma binară (valoarea numerică) a unui şir de cifre zecimale de "orice" lungime. Programul de mai sus este scris folosind sintaxa specifică asamblorului GAS; dar este relativ uşor de rescris de exemplu pentru TASM ("movl $10,%ecx" trebuie rescris ca "mov ecx, 10"; "movb (%edi),%bl" ca "mov BL, [EDI]", etc.) şi de altfel, există (pe Internet) programe de conversie între sintaxa AT&T (utilizată de GNU) şi sintaxa Intel (utilizată de TASM). Subrutina lg_fact calculează (angajând coprocesorul) lg(N!) şi determină apoi numărul de cifre (de câte 16 biţi) ale reprezentării factorialului în baza 2^16 (vezi la începutul articolului, "Lungimea factorialului"); printr-un calcul analog, subrutina lg_nw_z4 determină numărul de cifre (de câte 16 biţi) ale reprezentării factorialului în baza 10^4. Am redat aici un screenshot parţial de pe o instanţă de lucru cu Insight Debugger (analog lui Turbo Debugger din Borland C++). Se văd regiştrii microprocesorului (Intel x86) şi ai coprocesorului; după executarea primelor două instrucţiuni de la adresa Pentru fiecare proces încărcat, sistemul (kernelul Linux) face o alocare iniţială de memorie, până la o anumită adresă (numită "the system break"); de obicei, zona alocată cuprinde trei categorii de memorie: stack, heap şi memorie "mmap"-ată. Memoria stack ("stivă") este gestionată de către sistem (nu de către procesele individuale); microprocesorul oferă pentru aceasta regiştrii ESP ("stack pointer", care indică vârful curent al stivei) şi EBP ("base pointer", pentru a referi parametrii din stivă) şi un număr de instrucţiuni care ajustează automat ESP: push şi pop pentru a depune/scoate o valoare pe/din stivă, cu decrementare sau incrementare automată a EIP; ret care încarcă în EIP ("instruction pointer") valoarea din vârful stivei, considerată a fi o "adresă de revenire"; call <adresă-funcţie> care încarcă în stivă adresa de revenire şi apoi dă controlul funcţiei apelate; etc. Memoria heap şi cea "mmap-ată" rămân alocate pe toată perioada existenţei procesului şi pot fi eventual extinse/îngustate în timpul execuţiei, folosind apeluri de sistem ca brk() sau mmap(). brk() serveşte pentru schimbarea dimensiunii spaţiului de date, primind ca parametru noua adresă de "system break" pentru memoria heap; dar, în condiţiile concrete existente pe sistemul propriu (şi fiind vorba de lucrul la 'amifac') am verificat (validând oarecum şi prin consultarea Internetului) că brk() "merge" fără probleme doar dacă dimensiunea zonei solicitate pentru alocare (în heap) este mai mică decât 127 Ko (altfel, au apărut nişte probleme de adresare a memoriei alocate, de genul SIGSEGV - "segment violation"). mmap() are următorul prototip (în /sys/mman.h): şi asigură o corespondenţă în memoria fizică a porţiunii din fişierul cu descriptorul filedes (returnat de apelul prealabil open(...)) care este cuprinsă între octetul din fişier indicat de address (primul parametru) şi cel de la adresa address + length -1; mmap() returnează adresa la care a fost mmap-at fişierul (sau -1, în caz de eroare). În cazul când se doreşte o alocare "obişnuită" de memorie (neconectată pe un fişier propriu-zis), trebuie transmis filedes = -1 (sau 0), addesss = NULL, offset = 0 şi desigur, trebuie specificat ca flags "MAP_ANONYMOUS" (fişier "anonim"), iar protect = PROT_READ | PROT_WRITE (drepturi de citire/scriere). Toate aplicaţiile au sau pot să aibă nevoie de o serie de "servicii" standard, care în general trebuie să interacţioneze direct cu hardware-ul sistemului: să creeze un fişier pe disk, să deschidă un fişier pentru citire sau scriere, să aloce mai multă memorie, etc.; tocmai pentru a putea fi utilizate în siguranţă de către oricare aplicaţie, asemenea servicii au fost încorporate în "nucleul" sistemului de operare (iar aplicaţiile individuale nu mai trebuie să se preocupe de scrierea funcţiilor respective, putând să apeleze la cele încorporate deja în kernel). Mecanismul standard prin care se pot folosi serviciile din kernel se bazează pe următoarele elemente: - la iniţializarea sistemului, se creează în memorie un tabel de întreruperi în care se înregistrează adresele serviciilor (a funcţiilor corespunzătoare) puse la dispoziţie de kernel; - instrucţiunea int 0x80 (iar pentru sistemul de operare DOS, INT 0x21) întrerupe execuţia procesului curent şi kernelul preia controlul: salvează toţi regiştrii (exceptând EAX), caută în tabelul de întreruperi adresa corespunzătoare numărului de ordine primit în registrul EAX (vezi linia - la încheierea execuţiei serviciului respectiv, se reconstituie de pe stivă regiştrii (în timp ce EAX conţine valoarea de returnat, sau un cod de eroare) şi se redă controlul aplicaţiei care a cerut serviciul. Desigur, fiecare serviciu are nevoie de anumiţi parametri; aceştia sunt transmişi de către aplicaţia care apelează serviciul, de obicei în regiştri; dacă parametrii sunt în număr mai mare (cum e cazul funcţiei mmap()), ei sunt încărcaţi pe stivă şi se transmite (în EBX; vezi linia Observaţie. În subrutina de mai sus nu se face şi verificarea alocării (este posibil ca valoarea returnată să fie -1, adică "eroare de alocare"); dacă alocarea eşuează (dar... nu s-a întâmplat, în experimentele întreprinse) atunci procesul este pur si simplu distrus (nu se întâmplă nimic altceva...). Desigur, totdeauna este recomandabilă verificarea rezultatului! (Do as I say, not as I do). Ne propusesem la începutul articolului, să modelăm recursiv calculul factorialului; dar lucrând direct în limbaj de asamblare, implicarea unui mecanism standard de recursivitate devine artificială. Ar fi însă de menţionat o schemă de modelare recursivă care este posibilă numai în limbaj de asamblare (şi care elimină necesitatea constituirii "în adâncime" a cadrelor stivă corespunzătoare reapelării funcţiei): push adresa_de_reluare şi ret (explicaţia mecanismului: RET încarcă în EIP adresa din vârful stivei - unde tocmai s-a încărcat 'adresa_de_reluare' - şi ca urmare se trece la executarea codului de la adresa respectivă); lucrând numai cu regiştrii, nu mai trebuie să creem cadre-stivă pentru fiecare reapelare - însă cele două instrucţiuni necesare (push şi ret) consumă împreună de câteva ori mai mult timp decât simplul "JMP adresa_de_reluare". Programul se poate folosi ca în exemplul următor: Nu ne-am preocupat suficient de diverse optimizări posibile: - s-ar fi putut evita înmulţirile cu 0 (factorialele se termină cu din ce în ce mai multe zerouri); - presupunând n >> 13, se puteau evita 10 înmulţiri: după ce s-a obţinut produsul "mare" n*(n-1)*...*13, în loc de a continua *12*11*...*2 se putea continua cu o singură înmulţire, anume cu 479001600 = 12! ("încape" pe 32 de biţi; 13! depăşeşte 32 biţi lungime); - şi se mai puteau evita încă 6 înmulţiri, înlocuind *19*18*...*13 printr-o singură înmulţire (cu 13*...*19, care este mai scurt de 32 biţi); cu alte cuvinte, factorii n, n-1, ..., 2 (sau măcar cei mai mici ca 1000, ori chiar cei sub 10000) ar fi trebuit "grupaţi" în prealabil, înlocuindu-i cu produse parţiale care să nu depăşească fiecare, 32 de biţi (încât n! ar fi rezultat prin mult mai puţine înmulţiri de "număr mare" cu factor de 32 biţi). Oricum, 10000! se obţine aproape instantaneu, iar 20000! ia 3-4 secunde; calculul 60000! ajunge la 40 secunde. Obs. Nu se pot obţine corect valori n! pentru n > 2^16: la modelarea înmulţirii din FAC2 - vezi comentariul de la amifac (fişierul executabil rezultat după make) măsoară 2.7 KB; pe lângă codul propriu-zis, conţine informaţie de depanare, tabelul de simboluri şi informaţie specifică formatului de "executabil". Putem dezasambla "zona de cod", folosind de exemplu objdump: În acest listing, prima coloană indică adresele la care sunt asamblate instrucţiunile, a doua coloană conţine codurile ("codul maşină") instrucţiunilor, iar a treia coloană indică instrucţiunile în limbaj de asamblare; de exemplu, la adresa 0x8048241 este asamblată instrucţiunea int Secţiunea ".text" începe la adresa 0x8048074 şi conţine codurile funcţiilor _start(), edi_toi(), etc. (dispuse consecutiv). Deci dimensiunea întregului cod este 0x8048245 - 0x8048074 +1 = 0x246 - 0x74 = 0x1D2 = 466 octeţi (deşi programul părea lung - cu totul fiind 220 de rânduri). Dar asemenea informaţii (lungimea codului), precum şi alte informaţii sintetice despre executabil, putem obţine direct folosind readelf: Vedem de exemplu, că "amifac" este un fişier executabil (cu instrucţiuni executabile) în format ELF Executable and Linking Format, adresat unei "Machine" Intel 80386 (minimum), cu arhitectură pe 32 de biţi ("Class: ELF32"; fişiere şi spaţiu de adrese de până la 4 GB), cu sistem de operare UNIX (compatibil), având formatul de date "little endian"; secţiunea ".text" are atributele "AX" (este reAlocabilă şi conţine instrucţiuni eXecutabile) şi are size = 0x1d2 (cum rezultase şi folosind objdump), fiind "aliniată" (ca şi ".data") la adrese multiplu de 4 bytes ("Al = 4"); tabelul de simboluri (".symtab", care înregistrează informaţii de legare: adresele simbolurilor, numele lor, etc.) măsoară 0x250 octeţi.
[1] Vlad Bazon - "Reprezentarea binară a numerelor mari", Gazeta de informatică nr.8/2000
'Bignum' - modelare OOP în perl, folosind baza 10k (k = 6)
package Bignum; # analog cu declaraţia de "class" în C++ (class Bignum { ... })!
use strict; # restricţionează construcţiile (de variabile, de exemplu) "nesigure"
# "my" serveşte pentru a aloca memorie (şi identificator) pentru o variabilă locală
# $CIFRA şi $BAZA fiind create cu "my", nu vor putea fi accesate din exterior
my $CIFRA = 6; # numărul de cifre zecimale care "încap" într-o "cifră" din noua bază
my $BAZA = int "1e$CIFRA"; # $BAZA = 10**$CIFRA
# (în "notaţia ştiinţifică", 10**6 este '1e6')
sub new { # "Constructorul" de obiecte: my $obj = Bignum->new("1234567890000000000");
my ($class, $nrz) = @_; # primul parametru este un "pointer" la clasa definită
# (analog cu 'this' din C)
# @_ este tabloul parametrilor transmişi subrutinei
# (analog cu 'argv' din C)
my $h = length $nrz; # lungimea şirului de cifre zecimale primit ca parametru
my $R = $h % $CIFRA; # $nrz va fi reprezentat prin $D valori "longint"
# (câte $CIFRA cifre), plus încă una, dacă rămâne un rest
my $D = int($h / $CIFRA); # de mai puţin de $CIFRA cifre zecimale.
bless [ reverse( unpack( "A$R" . ("A$CIFRA" x $D), $nrz ) ) ], $class;
}
my $obj = Bignum->new("123"); - bless va înregistra $obj ca aparţinând clasei "Bignum" (astfel, $obj va avea acces la datele şi metodele din "Bignum.pm").
bless returnează obiectul construit, permiţând astfel "înlănţuirea" metodelor: print Bignum->new("123")->mul_int(1234); (presupunând că am avea o metodă "mul_int" definită în "Bignum.pm").$nz; unpack este analog cu 'printf' din C: primeşte un şablon de formatare şi transformă pe baza lui datele indicate. De exemplu, unpack('A2'.('A3' x 4), '12345678912345') produce tabloul numeric: [12, 345, 678, 912, 345].$, componentele tabloului se accesează folosind $arr[$i], unde indexul $i este 0 pentru primul element, etc. Indecşii negativi accesează tabloul de la sfârşit (print $arr[-1] va produce 'abcd').
Creează un nou tablou @clone, în care copiază elementele din @arr (context listă).$len_arr = @arr; sau my $len_arr = scalar @arr; Variabila "scalară" $len_arr (nu-i tablou!) primeşte ca valoare numărul de elemente ale tabloului @arr (context scalar).$ref_arr = \@arr; Variabila $ref_arr primeşte ca valoare o referinţă ("pointer") la tabloul @arr. Componentele tabloului pot fi accesate prin intermediul referinţei create, folosind operatorul "săgeată" (ca şi în C): $ref_arr->[-2] este valoarea 3.25 şi la fel, $ref_arr->[1].$ref_sapt = [ "luni", "marţi", "joi" ]; Variabila $ref_sapt nu este un tablou (are sigiliul '$' şi nu '@'); în partea dreaptă avem o listă de trei valori (deci, un tablou) încadrată însă nu de '( )' ca la un tablou obişnuit, ci de '[ ]'; avem astfel, un tablou anonim şi variabila scalară $ref_sapt permite referirea valorilor din tablou ($ref_sapt este o referinţă la tablou): $ref_sapt->[2] este valoarea "joi".$obj->[0]). Putem testa "bucata" de mai sus direct din linia de comandă a shell-ului:
vb@debian:~/lar$ perl -MBignum -e 'print Bignum->new("123456789")->[0],"\n"'
456789
vb@debian:~/lar$ perl -MBignum -e 'print Bignum->new("123456789")->[1],"\n"'
123
vb@debian:~/lar$
sub mul_int {
my ($self, $n) = @_; # $n este factorul cu care trebuie înmulţit $self
my $th = @{$self}; # numărul de elemente din tabloul referit de $self
# Prima trecere: înmulţeşte fiecare valoare din tablou cu $n
foreach (@{$self}) { $_ *= $n; } # 'foreach' parcurge tabloul;
# $_ corespunde elementului curent
# A doua trecere: se reduce modulo $BAZA fiecare valoare, propagând transportul
foreach my $i (0 .. $th - 1) { # '..' generează lista (0,1,2,..., $th-1)
my $q = $self->[$i];
if($q >= $BAZA) {
$n = int($q / $BAZA); # transportul
$self->[$i] = $q % $BAZA; # reduce modulo $BAZA
$self->[$i+1] += $n; # la valoarea din dreapta, se cumulează transportul
}
}
if($th > 1 && $self->[$th - 1] >= $BAZA) { # reducerea aferentă ultimei valori
$self->[$th] = int($self->[$th - 1] / $BAZA); # extinde tabloul cu încă o cifră
$self->[$th - 1] %= $BAZA; # (transportul final)
}
return $self; # returnează obiectul (referinţă), permiţând "înlănţuiri" de metode
}
sub to_string {
my $self = shift; # referinţa la tabloul numeric
# soluţia directă cere un şablon dificil de formulat:
# my $fz = pack("(A$CIFRA)*", reverse(@{$self}));
my $th = @{$self} - 1; # adoptă exact soluţia dată mai sus la "javascript"
my $fz = "" . $self->[$th]; # operatorul de concatenare este "." ("+" în javaScript)
while(--$th >= 0) {
my $c = "" . $self->[$th];
while(length($c) < $CIFRA) {
$c = '0' . $c;
}
$fz .= $c;
}
return \$fz; # returnează o referinţă la şirul cifrelor zecimale
}
1; # cerut pentru a indica încheierea modulului
vb@debian:~/lar$ \
perl -MBignum -e 'print Bignum->new("123456789")->mul_int(1000)->to_string'
SCALAR(0x81874e0)vb@debian:~/lar$
vb@debian:~/lar$ \
> perl -MBignum -e 'print ${Bignum->new("123456789")->mul_int(1000)->to_string}'
123456789000vb@debian:~/lar$
#! /usr/bin/perl -w
use Data::Dumper; # serializează (returnând ca şir formatat) structuri de date perl
use Bignum; # încarcă modulul definit mai sus
my $n = Bignum->new("1234567891234000000000"); # creează un obiect
warn Dumper($n, $n->to_string, ${$n->to_string}); # investighează obiectul construit
vb@debian:~/lar$ ./btest-dump.pl # lansează programul (după "chmod +x" pe fişier)
$VAR1 = bless( [ # corespunde lui $n (primul în lista parametrilor lui Dumper)
'000000',
'234000',
'567891',
'1234'
], 'Bignum' );
$VAR2 = \'1234567891234000000000'; # pentru $n->to_string (referinţă)
$VAR3 = '1234567891234000000000'; # pentru ${$n->to_string} (după dereferenţiere)
Calculul factorialelor, angajând un obiect 'Bignum'
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#! /usr/bin/perl
use Bignum;
use Text::Autoformat qw(autoformat break_at);
my $nr = $ARGV[0] || 100; # numărul (sau 100) pentru care cerem factorialul
sub factorial {
$_[1] == 1 ? $_[0] : factorial($_[0]->mul_int($_[1]), $_[1]-1);
}
open(FH, ">>", "bigfac.txt");
print FH `date +%T`, $nr . "! = \n";
my $fac = ${factorial(Bignum->new(1), $nr)->to_string};
my $format = autoformat $fac, {left => 1, right => 80, break => break_at('')};
print FH $format, $nr . "! are " . length($fac) . " cifre zecimale. ", \
`date +%T`, "-" x 80, "\n";
`date +%T` din liniile 13 şi 20 asigură înscrierea în fişier a timpului orar (H:M:S) de începere şi respectiv de încheiere a apelării funcţiei "factorial"; caracterul "apostrof invers" se foloseşte pentru a apela o comandă Linux, în cazul de faţă comanda date prin care Linux afişează data curentă şi timpul orar actual (desigur, în loc de a apela la serviciile sistemului - că atunci, programul nu mai este portabil - se putea folosi de exemplu modulul perl Class:Date; dar şi mai bine era folosirea unui modul pentru "benchmark", ca Test::Benchmark).6) C şi C++
sizeof(short int)).Folosirea bibliotecii GMP
Proiectul GNU
Instalarea bibliotecii GMP
vb@debian:~$ cd gmp-4.2.1 # intră în directorul "gmp-4.2.1", ca user obişnuit
vb@debian:~/gmp-4.2.1$ ./configure
# lansează scriptul de configurare a compilării, existent în "gmp-4.2.1"
# rezultă fişierul "Makefile" (descrie relaţiile dintre fişierele de compilat)
vb@debian:~/gmp-4.2.1$ make
# execută comenzile de compilare găsite în fişierul "Makefile"
vb@debian:~/gmp-4.2.1$ make check
# auto-testare de completitudine şi corectitudine a fişierelor rezultate
vb@debian:~/gmp-4.2.1$ sudo make install
sudo, prin care userul "obişnuit" se poate substitui unui alt user (în cazul de faţă, lui "root").Programul de factoriale, folosind GMP
1
2
3
4
5
6
7
8
9
10
11
12
#include <stdio.h> // în /usr/include/
#include <stdlib.h>
#include <gmp.h> // în /usr/local/include/
int main ( int argc, char** argv ) { // apelează ca: factorial 100
// (pentru a obţine 100!)
mpz_t factorial;
mpz_init( factorial );
mpz_fac_ui( factorial, atoi(argv[1]) );
gmp_printf( "%Zd\n", factorial );
return EXIT_SUCCESS; // stdlib.h prevede #define EXIT_SUCCESS 0
}
vb@debian:~/lar$ gcc factorial.c -lgmp -o fact-gmp
-l a servit ("-lgmp") pentru a cere "legarea" codului programului, de biblioteca libgmp.a (rezultată în /usr/local/lib/ prin compilarea prezentată anterior, a surselor GMP); -o permite specificarea unui fişier pentru codul rezultat prin compilare şi link-are.
vb@debian:~/lar$ ./fact-gmp 100
9332621544394415268169923885626670049071596826438162146859296389521759999322991
5608941463976156518286253697920827223758251185210916864000000000000000000000000
vb@debian:~/lar$ ./fact-gmp 100000 > fac-100000.txt /* cu redirectarea scrierii */
mpz_t (vezi programul de mai sus, linia 7) etc. sunt "tipuri" specifice GMP şi pot fi lămurite investigând fişierul header gmp.h (şi studiind manualul GMP):// Definiţii extrase din /usr/local/include/gmp.h
typedef unsigned long int mp_limb_t;
typedef struct
{
int _mp_alloc; /* Number of *limbs* allocated and pointed to by the _mp_d field. */
int _mp_size; /* abs(_mp_size) is the number of limbs the last field points to. */
mp_limb_t *_mp_d; /* Pointer to the limbs. */
} __mpz_struct;
typedef __mpz_struct mpz_t[1];
void mpz_fac_ui (mpz_ptr, unsigned long int);
limbs', un pointer la tabloul care conţine valorile limbs respective şi un număr care indică dimensiunea zonei alocate curent pentru limbs (nu întreaga zonă este şi "ocupată", la un moment sau altul).
GMP face o analogie între numerele întregi (sub cele două forme de reprezentare: cea uzuală în baza 10 şi respectiv, cea internă în bază mai mare) şi… corpul uman: corpul (numărul reprezentat intern) are mai multe membre ("limbs", cifre în baza internă de reprezentare) şi fiecare membru (o mână, de exemplu; sau, un "limb") are mai multe degete (cifre zecimale).mpz_fac_ui() oferită de GMP.'bignum' - modelare OOP în C++, folosind baza 2^16 (şi conversie la baza 10^4)
using namespace std declară valabilitatea în cadrul fişierului respectiv, pentru elementele din std ("Standard C++ Library"; astfel că se poate scrie "cout" în loc de "std::cout").#include <iostream>
using namespace std;
#define BAZA 65536 // 2^16 (cifrele sunt 0..65535, reprezentate pe câte 16 biţi)
#define LOBY(x) ((unsigned short int) ((x) & 0xFFFF)) // cifra LOW (biţii 0..15)
#define HIBY(x) ((unsigned short int) ((x) >> 16 & 0xFFFF)) // cifra HIGH (biţii 16..31)
int main() {
cout << "short int: " << sizeof(short int) << ",\tlong: " << sizeof(long) << endl;
unsigned long a; unsigned short aH, aL;
cin >> a; aH = HIBY(a); aL = LOBY(a);
cout << "cifra High = " << aH << ",\tcifra Low = " << aL << endl;
cout << aH << " * BAZA + " << aL << " = " << (unsigned long)(BAZA * aH + aL);
}
vb@debian:~/lar$ g++ -o test16 test16.cc
vb@debian:~/lar$ ./test16
short int: 2, long: 4
987654321
cifra High = 15070, cifra Low = 26801
15070 * BAZA + 26801 = 987654321
#include <iostream>
using namespace std;
#define BAZA 65536
#define LOBY(x) ((unsigned short int) ((x) & 0xFFFF))
#define HIBY(x) ((unsigned short int) ((x) >> 16 & 0xFFFF))
int main() { // înmulţeşte valoare 0..2^32-1 (32 biţi) cu valoare 0..2^16-1 (16 biţi)
unsigned long a; unsigned short int k;
cin >> a >> k;
unsigned long tmp; // pentru produsul a două cifre de câte 16 biţi
unsigned short prod[3]; // înregistrează cifrele produsului a*k (sunt maximum 3 cifre)
tmp = k * LOBY(a); // k * ("cifra unităţilor" lui a); rezultă maximum 32 biţi
prod[0] = LOBY(tmp); // "cifra unităţilor" produsului a*k
// "transportul" rezultă automat, în partea HIBY(tmp)
tmp = HIBY(a) * k + HIBY(tmp); // k * ("cifra zecilor" lui a) + "transportul"
prod[1] = LOBY(tmp); // "cifra zecilor" produsului a*k
prod[2] = HIBY(tmp); // "transportul final" devine cifra HIGH a produsului a*k
cout<<"cifrele produsului: "<< prod[2] << '\t' <<prod[1] << '\t' << prod[0] << '\n';
cout<<"produsul aprox.= : "<<double(prod[2])*BAZA*BAZA + prod[1]*BAZA + prod[0];
}
vb@debian:~/lar$ g++ -o test-mul test-mul.cc
vb@debian:~/lar$ ./test-mul
999999999 // deînmulţit
65535 // înmulţitor
cifrele produsului: 15258 36452 13825 // 3 cifre "unsigned short int"
produsul aprox.= : 6.55307e+13 // 15258*BAZA^2 + 36452*BAZA + 13825 = 65534999934465
#include <fstream>
using namespace std;
#define BAZA 0x10000L // 2 ^ 16 (cifre 0x0000..0xFFFF)
typedef unsigned short int word; // 0 .. 2^16 - 1
typedef unsigned long dword; // 0 .. 2^32 - 1
#define LOW(x) ((word) ((x) & 0xFFFF)) // biţii 0..15 ("Low word") din 'dword'
#define HIW(x) ((word) ((x) >> 16 & 0xFFFF)) // biţii 16..31 ("High word")
// presupune formatul "little_endian" (Intel)
class Bigfac {
private:
word * tw; long nw; // tw[] reprezintă numărul în baza 2^16 (cifră = "word")
word * z4; long n4; // z4[] reprezintă numărul în baza 10^4 (cifre 0000..9999)
void tw_to_z4(); // folosită de "<<" pentru conversie la baza 10 a valorii tw[]
public:
Bigfac(long); // calculează şi alocă necesarul de memorie pentru tw[]
~Bigfac(); // eliberează zona alocată lui tw[]
void tw_mul_w(word); // înmulţeşte tw[] cu numărul indicat
friend ostream & operator<<(ostream &, Bigfac &); // calculează z4[] şi scrie
};
#include "bigfac.h"
#include <math.h> // log10() serveşte calculul lungimii factorialului
Bigfac::Bigfac(long N) { // N >= n (când se cere n!)
double lgf = 0; // estimează numărul de cifre zecimale pentru N!
for(long k = 2; k <= N; k++) lgf += log10(k);
long nt = trunc(lgf/4.8) + 1; // maxim necesar pentru tw[]
tw = new word [nt];
for(long i = 0; i < nt; i++) // iniţializarea zonei alocate în 'heap'
tw[i] = 0;
tw[0] = 1; nw = 1; // tw[] este iniţializat cu 1!=1
n4 = 0; z4 = 0; // z4[] va fi alocat când se cere conversie la 10^4
}
Bigfac::~Bigfac() { // elimină din 'heap' tw[]
delete[] tw;
}
void Bigfac::tw_mul_w(word k) { // înmulţeşte tw[] cu k (algoritmul clasic)
dword car = 0; long i;
for(i = 0; i < nw; i++) {
car = tw[i]*k + HIW(car); // High(car) înregistrează automat 'transportul'
tw[i] = LOW(car);
}
word u = HIW(car);
if(u) { // dacă există transport final
nw++; tw[nw-1] = u;
}
}
void Bigfac::tw_to_z4() { // conversie tw[] (baza 0x10000) la baza 10000
word * Bn, * B, * S; // (adaptare după [2], unde se folosea baza 256)
word * Z, * T;
long lB, lD, lZ;
dword val;
lB = nw; Bn = new word[lB]; // creează o copie de lucru, a lui tw[]
B = Bn; // copiază tw[] în ordine inversă, în B[]
for(long i=0; i < lB; i++) B[i] = tw[lB - 1 - i];
lZ = long(lB*1.3)+1; // numărul maxim de 'cifre' pentru z4[]
Z = new word[lZ];
T = Z + (lZ -1); // T pointează Z[] de la sfârşit ("cifra unităţilor")
while(lB) {
val = 0; S = B; // S referă deîmpărţitul curent (dacă lB > 0, adică mai
lD = lB; // există cifre "de coborât" pentru a găsi noul cât parţial)
while(lD) {
val = val*BAZA + *S; // Câtul şi restul împărţirii (schema lui Horner)
*S = val / 10000; // lui B[] (deîmpărţitul "curent"), la noua bază 10000
val %= 10000;
lD--;
S++;
}
*T = val; // Înregistrează în Z[] restul (0..9999) împărţirii curente,
T--; // şi pointează locul următorului rest parţial
while(*B == 0 && lB) { // ignoră zerourile iniţiale (nesemnificative) din B[]
lB--; if(lB) B++;
}
}
lZ = (Z + lZ) - T - 1; // fixează Bigfac::z4 pe reprezentarea în baza 10^4 obţinută
z4 = ++T; n4 = lZ;
delete[] Bn; // elimină tabloul de lucru folosit (tw[] a rămas nemodificat)
}
ostream & operator<<(ostream & out, Bigfac & Fac) {
long nw = Fac.nw - 1;
out << Fac.nw <<" cifre în baza 2^16:\n"<< hex;
for(long i = nw; i >= 0; i--) // reprezentarea hexazecimală a valorii din tw[]
out << Fac.tw[i];
out << dec << endl;
Fac.tw_to_z4(); // obţine reprezentarea în baza 10^4 (în Fac.z4[])
// Cifrele din z4[] (exceptând pe prima) trebuie scrise în baza 10 cu 4 cifre zecimale,
// prefixând cu '0' valorile mai mici de 1000, cu '00' pe cele mai mici de 100, etc.
out << Fac.z4[0]; // cifra "high" din z4[] nu necesită prefixare cu '0'
for(long i=1; i < Fac.n4; i++) {
word w = Fac.z4[i];
if(w == 0) out << "0000";
else { // o cifră din z4[] ca '12', trebuie scrisă în baza 10 ca '0012'
word k = 1000;
while(w < k) { out << '0'; k /=10; }
out << w;
}
}
out<<endl;
return out;
}
vb@debian:~/lar$ g++ -o bigfac bigfac.h bigfac.cc bigfac-test.cc
vb@debian:~/lar$ ./bigfac // execută programul executabil rezultat
vb@debian:~/lar$ cat aaaa.txt // afişează conţinutul fişierului "aaaa.txt"
Unde am greşit? Păi nu la tw_mul_w(K), pentru că tot procedeul de înmulţire s-a bazat pe ideea "word" × "word"="dword", deci obligatoriu factorul K trebuie să fie "word"; am greşit la constructor - corect-corect (dar neobligatoriu) era să fi considerat N de tip "word" şi nu "long"…operator <<()" numai afişarea hexazecimală (comentând porţiunea care apela "tw_to_z4()", etc.), recompilând şi reexecutând - timpul pentru 65000! s-a redus la 20 secunde.
Prin urmare, două treimi din timpul de execuţie se datorează conversiei la forma uzuală a rezultatului, ceea ce şi justifică ideea de a afişa/returna rezultatul în hexazecimal. Pe de altă parte, rezultatul este mult inferior ca timp, celui obţinut cu o bibliotecă specializată, precum GMP.
Astfel că în prealabil, trebuie făcute două modificări: în "bigfac.h", prototipul void tw_mul_w(word); trebuie înlocuit cu Bigfac& tw_mul_w(word); pentru a permite formularea standard "if(n>1) factorial(fac.tw_mul_w(n), n-1)"; iar în "bigfac.cc" metoda Bigfac& Bigfac::tw_mul_w(word k) trebuie încheiată prin return *this;. Observăm că aceste modificări nu afectează programul de test iterativ "bigfac-test.cc" de mai sus. Având în vedere modificările indicate, programul de calcul recursiv se poate formula astfel:#include "bigfac.h" // "bigfac-test-rec.cc"
#include <iostream> // folosim Bignum::operator<<() cu ieşirea standard (ecran)
Bigfac& factorial( Bigfac& fac, word n ) { // formularea recursivă standard pentru n!
if(n == 1 ) return fac;
return factorial( fac.tw_mul_w(n), n-1 );
}
Bigfac fac(30000); // alocare în segmentul de "date globale"
int main() { word n;
cout<<"număr natural <= 10000: "; cin >> n;
// Bigfac fac(n); // (variantă) alocare în segmentul 'stack'
factorial(fac, n);
cout << n << "!=\n" << fac;
return 0;
}
vb@debian:~/lar$ g++ -o bigfac bigfac.h bigfac.cc bigfac-rec.cc
vb@debian:~/lar$ ./bigfac
număr natural <= 10000: 100
100! are 33 cifre în baza 2^16:
1b30964ec395dc2469528d54bbda40d16e966ef9a70eb21b5b2943a321cdf1039174557cca9420c
6ecb3b72ed2ee8b2ea2735c61a000000
40 cifre în baza 10^4:
9332621544394415268169923885626670049071596826438162146859296389521759999322991
5608941463976156518286253697920827223758251185210916864000000000000000000000000
7) Limbaje de asamblare (GNU binutils)
Planul şi intenţiile de lucru
conţinut depus pe stivă nivel în stivă numărul de argumente ('argc' în C) = 2 ESP + 16 pointer la numele programului (primul argument): "amifac" ESP + 12 pointer la şirul cifrelor numărului N (al doilea argument) ESP + 8 NULL (încheie lista argumentelor) ESP + 4 adresa de revenire (după încheierea execuţiei) ESP (Stack Pointer) AS = as # specifică asamblor (GNU as)
LD = ld # linker-ul (GNU ld)
ASFLAGS = -g -ahlsd # opţiunile de asamblare ('-g' include informaţie de depanare)
LDFLAGS = # opţiuni de link-are
RM = /bin/rm -f # calea programului de "ştergere" (a fişierelor inutile/vechi)
OBJS = amifac.o edi_toi.o lg_fac.o alloc_mem.o # fişierele "object"
PROG = amifac # numele programului executabil final
all: $(PROG) # obţii executabilul legând toate fişierele "object":
# asamblează cu AS (şi cu opţiuni ASFLAGS) fişierele *.s
$(PROG): $(OBJS)
$(LD) $(LDFLAGS) $(OBJS) -o $(PROG)%.s: %.s
$(AS) $(ASFLAGS) $<
clean: $(RM) $(PROG) $(OBJS)
De la şir de cifre ASCII-Z la "unsigned long"
# fişierul edi_toi.s
.globl edi_toi
edi_toi: # EDI = adresa şirului cifrelor lui N. Returnează EAX = N.
push %ebx # salvează pe stivă EBX, ECX, EDX
push %ecx
push %edx
movl $10, %ecx # ECX = 10
xorl %edx, %edx # iniţializează EDX = EAX = EBX = 0
xorl %eax, %eax
xorl %ebx, %ebx
ed1:
movb (%edi), %bl # BL = cifra ASCII pointată de EDI
test %bl, %bl # un şir ASCII-Z se încheie cu '\0'
jz ed2 # dacă BL=='\0' intră la adresa 'ed2'
subl $48, %ebx # BL = BL - '0'
mul %ecx # EDX:EAX = EAX * 10 + EBX
addl %ebx, %eax
inc %edi # pointează următoarea cifră
jmp ed1 # reia ("jump") de la adresa 'ed1'
ed2:
popl %edx # reconstituie EDX, ECX, EBX de pe stivă
popl %ecx
popl %ebx
ret # IP ("Instruction Pointer") = adresa de revenire
Numărul cifrelor din reprezentările 2^16 şi 10^4
# fişierul lg_fac.s
.globl lg_fact
lg_fact: # (ESP+4) conţine iniţial N şi în final numărul cifre 2^16 pentru N!
fldz # iniţial suma_lg(k!) este 0.0 (k=N..2)
qont:
fldlg2 # st(0)=lg(2), st(1)=suma_lg(i!) cu i=N..k-1
fildl 4(%esp) # st(0)=k (factorul N..2), st(1)=lg(2), st(2)=suma_lg(i!)
fyl2x # st(0)=lg(k), st(1)=suma_lg(i!) cu i=N..k-1
faddp %st, %st(1) # st(0)=suma_lg(i!) cu i=N..k
decl 4(%esp) # următorul factor N..2 (k--)
cmpl $1, 4(%esp)
jne qont # reia, dacă k>1
# în final st(0) = suma_lg(k!) cu k=2..N
fldlg2 # st(0) = lg(2), st(1) = suma_lg(k!)
fadd %st, %st # st(0) = 2*lg(2), st(1)=suma_lg(k!)
fadd %st, %st # st(0) = 4*lg(2), st(1)=suma_lg(k!)
fadd %st, %st
fadd %st, %st # st(0) = 16*lg(2) = lg(2^16), st(1)=suma_lg(k!)
fxch # interschimbă st(0) cu st(1)
fdivp %st, %st(1) # st(0) = suma_lg(k!) / lg(65536) = nw =
fistpl 4(%esp) # = numărul de "cifre" în baza 2^16 pentru N!
ret
.globl lg_nw_z4 # (ESP+4) conţine nw = numărul cifrelor 2^16 din tw[]
lg_nw_z4: # se determina numărul de cifre 10^4 corespunzător lui nw
fldz # lungimea necesară rezultă din 10^(4*Z) = 2^(16*nw)
fldlg2 # st(0) = lg(2)
fadd %st, %st # st(0) = 2*lg(2)
fadd %st, %st # st(0) = lg(16)
fildl 4(%esp) # st(0) = nw, st(1) = lg(16) (= lg(2^16) / 4)
fmul %st(1), %st # st(0) = nw * lg(16) = nr. word-uri necesare
fistpl 4(%esp) # reprezentării 10^4, pentru tw[]
movl 4(%esp), %eax # returnează rezultatul în EAX
ret
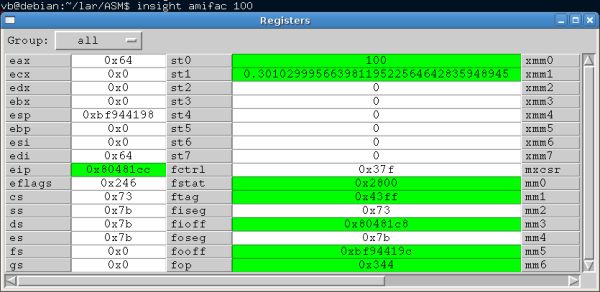
qont: din listingul de mai sus, st(0) conţine 100 (parametrul cu care s-a apelat 'amifac'), iar registrul st(1) conţine lg(2).Serviciul de alocare a memoriei
void* mmap(void* address, size_t length, int protect,
int flags, int filedes, off_t offset);
# fişierul alloc_mem.s
.equ SYS_mmap, 90
.globl me_mmap
me_mmap:
movl %esp, %ebp
subl $24, %esp # mmap() va prelua cei 6 parametri din stivă
movl 4(%ebp), %eax # numărul de Word-uri de alocat
addl $2, %eax # eventual, cu 2 mai mult decât s-a estimat
sall $1, %eax # dublează (un Word = 2 BYTES)
# se vor aloca EAX bytes, apelând mmap()
xorl %edx,%edx
movl %edx, (%esp) # NULL (offset_1, alocat de sistem)
movl %eax, 4(%esp) # dimensiunea fişierului (în Bytes)
movl $3, 8(%esp) # PROT_READ | PROT_WRITE
movl $0x22, 12(%esp) # MAP_PRIVATE | MAP_ANONYMOUS
movl $-1, 16(%esp) # descriptorul fişierului (-1 sau 0, pentru anonim)
movl %edx, 20(%esp) # offest_2 (zero)
movl $SYS_mmap, %eax
movl %esp, %ebx # EBX referă cadrul stivă care conţine cei 6 parametri
int $0x80 # mmap() returnează adresa zonei alocate în EAX
movl %ebp, %esp
ret
movl $SYS_mmap, %eax) şi încarcă adresa respectivă în EIP - astfel încât subrutina respectivă (care deserveşte întreruperea) este pusă în execuţie;movl %esp, %ebx) adresa cadrului stivă care îi conţine.Subrutina de calcul a factorialului
# fişierul amifac.s (Vlad Bazon, 2007)
.include "def.s"
.data
.align 4
zq4: .byte 0x30,0x30,0x30,0x30 # prefixare cu zerouri a unei cifre 10^4
nw: .long 1 # numărul de cifre (de câte 16 biţi) din tw[]
tw: .long 0 # adresa alocată reprezentării 2^16 a factorialului
.text
.align 4
.globl _start
_start:
movl 8(%esp), %edi # EDI = adresa şirului de cifre ale numărului N
call edi_toi
movl %eax, %edi # EDI = N (%edi nu este modificat de lg_fac(), me_mmap())
pushl %eax # încarcă N pe stivă# (ESP) = N
call lg_fact # (ESP) = numărul de cifre pentru tw[] (câte 2 BYTES)
call me_mmap # alocă 'virtual memory' pentru tw[] (2*(ESP)+2 BYTES)
movl %eax, tw # 'tw' va adresa zona alocată pentru tw[]
movl $1, (%eax) # iniţializează tw[] cu 1! = 1
popl %eax # descarcă stiva
cmpl $1, %edi # EDI a păstrat N# EDI = factorul n curent (iniţial n=N)
movl nw, %esi # ESI = nw# iniţial, nw=1
movl tw, %ebx # EBX = adresa de bază a tw[]
jbe ENDF # încheie când n == 1
FAC1:
xorl %edx, %edx # EDX va gestiona transporturile
xorl %ecx, %ecx # EBX + 2*ECX va referi cifra curentă din tw[]
FAC2:
movzwl (%ebx, %ecx, 2), %eax # EAX = cifra curentă din tw[]
shrl $16, %edx # DX = HIW('car')
imull %edi, %eax # EAX = n * cifra curentă (? pp. n < 2^16 ?)
addl %eax, %edx # şi adaugă transportul
movw %dx, (%ebx, %ecx, 2) # înscrie tw[k] = LOW('car')
incl %ecx # referă următoarea cifră din tw[]
cmpl %esi, %ecx
jne FAC2 # reia, dacă în tw[] mai există cifre neoperate
shrl $16, %edx # există transport final?
test %edx, %edx
je FAC3
movw %dx, (%ebx, %esi, 2) # înscrie transportul final în tw[]
incl %esi # şi incrementează contorul ESI (adică nw)
FAC3:
subl $1, %edi # n-- (următorul factor)
cmpl $1, %edi
jne FAC1 # "#reapelează"# factorial(n-1)
movl %esi, nw # 'nw' = numărul exact de cifre în baza 2^16 din tw[]
ENDF: # inversează tw[] ('swap' între stânga şi dreapta)
movl tw, %edi # EDI referă primul BYTE din tw[]
shll $1, %esi # adresa ultimului BYTE = EDI + 2*nw - 1
subl $2, %esi # ESI = 2*nw - 2
addl %edi, %esi # ESI referă penultimul BYTE din tw[]
SWAP: # (EDI) <--> (ESI), EDI += 2 şi ESI -= 2, până când EDI >= ESI
movw (%edi), %ax # AX = (EDI)
xchgw (%esi), %ax # (ESI) = AX, AX = (ESI)
stosw # (EDI) = AX şi EDI += 2
subl $2, %esi # ESI -= 2
cmpl %esi, %edi # repetă interschimbarea dacă EDI <# ESI
jb SWAP
# z4[] = reprezentarea 10^4 (câte 2 BYTES) a lui tw[]
pushl nw
call lg_nw_z4 # estimarea numărului de cifre 10^4
call me_mmap # alocă memorie pentru z4[]
popl %ebx
movl %eax, %edi # EDI = adresa de bază a tabloului alocat
movl nw, %ecx # ECX = nw (va contoriza 'nw' pt. deîmpărţitul tw[] curent)
movl tw, %esi # ESI referă deîmpărţitul tw[] curent, de la prima cifră (HIGH)
movl $10000, %ebx # se va împărţi prin noua bază, 10^4
xorl %ebp, %ebp # EBP va contoriza cifrele înregistrate în z4[]
P2:
pushl %ecx # determină câtul şi restul împărţirii (schema lui Horner)
pushl %esi # lui tw[] (deîmpărţitul "curent"), la noua bază 10000
xorl %edx, %edx
P3:
sall $16, %edx
movzwl (%esi), %eax
addl %edx, %eax
xorl %edx, %edx
divl %ebx
movw %ax, (%esi) # câtul curent intră în constituţia viitorului deîmpărţit parţial
addl $2, %esi
loop P3
movw %dx, (%edi) # înscrie restul împărţirii curente
addl $2, %edi
incl %ebp # contorizează cifrele înscrise
popl %esi # reconstituie adresa de bază a deîmpărţitului curent
popl %ecx # şi lungimea lui
P4:
movw (%esi), %ax # testează dacă au apărut zerouri nesemnificative în deîmpărţit
testw %ax, %ax
jnz P2
addl $2, %esi # ignoră cifrele zero iniţiale din deîmpărţitul curent
decl %ecx # corectând lungimea deîmpărţitului curent
jnz P4
subl $2, %edi
movl %edi, %esi # ESI referă penultimul BYTE din z4[]
movl %ebp, %ecx # ECX = numărul cifrelor (de câte 16 biţi) din z4[]
QQ:
movw $10, %bx # noua bază (ca împărţitor)
movw (%esi), %ax # cifra curentă din z4[], de convertit la cele 4 cifre zecimale
movl $zq4, %ebp # EBP referă zona '0000' unde se vor înscrie cifrele zecimale
movl $0x30303030, (%ebp)
addl $4, %ebp # începând de la dreapta (de la cifra unităţilor)
Q1:
xorw %dx, %dx # împarte DX:AX la 10,
divw %bx
addb $48, %dl # transformă ASCII restul DL,
decl %ebp
movb %dl, (%ebp) # înscrie cifra zecimală,
testw %ax, %ax
jnz Q1 # repetă cât timp câtul AX > 0
pushl %ecx # scrie cele 4 cifre zecimale înregistrate în zona zq4
movl $SYS_write, %eax # EAX = numărul serviciului 'write'
movl $STDOUT, %ebx # EBX = descriptorul fişierului în care se scrie
movl $zq4, %ecx # ECX = adresa sursei (datele de scris)
movl $4, %edx # EDX = lungimea sursei
int $0x80 # apelează la kernel pentru serviciul EAX
popl %ecx
subl $2, %esi # repetă pentru cifra următoare din z4[]
loop QQ
movl $SYS_exit, %eax # apelează serviciul de încheiere a procesului
xorl %ebx, %ebx
int $0x80
vb@debian:~/lar/ASM make /* execută comenzile din 'Makefile' */
make: Circular amifac.s <- amifac.s dependency dropped.
as -g -ahlsd -o amifac.o amifac.s /* asamblarea fiecărui fişier */
/* ... urmează aici listingurile de asamblare ale fişierelor ... */
ld amifac.o edi_toi.o lg_fac.o alloc_mem.o -o amifac /* leagă codurile */
vb@debian:~/lar/ASM$ ./amifac 100 # execută programul
00933262154439441526816992388562667004907159682643816214685929638952175999932299
15608941463976156518286253697920827223758251185210916864000000000000000000000000
vb@debian:~/lar/ASM$ ./amifac 30000 > fact.30000 /* acum, cu redirectarea ieşirii */
FAC2 încadrat de ? - am adoptat doar cea mai simplă soluţie; vom relua altă dată, pentru a ţine cont de toate aceste observaţii şi corecturi.Informaţii despre fişierul executabil
vb@debian:~/lar/ASM$ objdump -d amifac /* > amifac.lst (redirectare pe fişier) */
amifac: file format elf32-i386
Disassembly of section .text:
08048074 <_start>:
8048074: 8b 7c 24 08 mov 0x8(%esp),%edi
8048078: e8 23 01 00 00 call 80481a0
$0x80, prin codul de doi octeţi 0xcd, 0x80 (şi în continuare, la adresa 0x8048243 urmează codul de trei octeţi al instrucţiunii mov %ebp, %esp).
vb@debian:~/lar/ASM$ readelf -a amifac /* > amifac.lst.elf (redirectare pe fişier) */
ELF Header:
Magic: 7f 45 4c 46 01 01 01 00 00 00 00 00 00 00 00 00
Class: ELF32
Data: 2's complement, little endian
Version: 1 (current)
OS/ABI: UNIX - System V
ABI Version: 0
Type: EXEC (Executable file)
Machine: Intel 80386
Version: 0x1
Entry point address: 0x8048074
Start of program headers: 52 (bytes into file)
Start of section headers: 1540 (bytes into file)
Flags: 0x0
Size of this header: 52 (bytes)
Size of program headers: 32 (bytes)
Number of program headers: 2
Size of section headers: 40 (bytes)
Number of section headers: 10
Section header string table index: 7
Section Headers:
[Nr] Name Type Addr Off Size ES Flg Lk Inf Al
[ 0] NULL 00000000 000000 000000 00 0 0 0
[ 1] .text PROGBITS 08048074 000074 0001d2 00 AX 0 0 4
[ 2] .data PROGBITS 08049248 000248 00000c 00 WA 0 0 4
[ 3] .debug_aranges PROGBITS 00000000 000258 000080 00 0 0 8
[ 4] .debug_info PROGBITS 00000000 0002d8 000104 00 0 0 1
[ 5] .debug_abbrev PROGBITS 00000000 0003dc 000050 00 0 0 1
[ 6] .debug_line PROGBITS 00000000 00042c 00017c 00 0 0 1
[ 7] .shstrtab STRTAB 00000000 0005a8 00005c 00 0 0 1
[ 8] .symtab SYMTAB 00000000 000794 000250 10 9 29 4
[ 9] .strtab STRTAB 00000000 0009e4 0000b6 00 0 0 1
Key to Flags:
W (write), A (alloc), X (execute), M (merge), S (strings)
---etc.-------
Program Headers:
Type Offset VirtAddr PhysAddr FileSiz MemSiz Flg Align
LOAD 0x000000 0x08048000 0x08048000 0x00246 0x00246 R E 0x1000
LOAD 0x000248 0x08049248 0x08049248 0x0000c 0x0000c RW 0x1000
---etc.-------
Symbol table '.symtab' contains 37 entries:
Num: Value Size Type Bind Vis Ndx Name
---etc.-------
7: 00000001 0 NOTYPE LOCAL DEFAULT ABS SYS_exit
---etc.-------
12: 08049248 0 NOTYPE LOCAL DEFAULT 2 zq4
13: 0804924c 0 NOTYPE LOCAL DEFAULT 2 nw
14: 08049250 0 NOTYPE LOCAL DEFAULT 2 tw
15: 080480da 0 NOTYPE LOCAL DEFAULT 1 ENDF
16: 080480a7 0 NOTYPE LOCAL DEFAULT 1 FAC1
---etc.-------
29: 080481ee 0 NOTYPE GLOBAL DEFAULT 1 lg_nw_z4
30: 08048208 0 NOTYPE GLOBAL DEFAULT 1 me_mmap
31: 08048074 0 NOTYPE GLOBAL DEFAULT 1 _start
32: 080481a0 0 NOTYPE GLOBAL DEFAULT 1 edi_toi
---etc.-------
Bibliografie
[2] Vlad Bazon - "Limbaje şi calculator", Ed. PETRION 1998
vezi Cărţile mele (de programare)