Rezolvarea unei probleme de matematică poate fi sugerată de rezultatele investigaţiei printr-un program adecvat. Pentru exemplu, considerăm următoarea problemă (nu neapărat dificilă): să se arate că următorul şir este convergent şi să i se determine limita:

$$x_n=\frac{1}{n^2+1}+\frac{2}{n^2+2}+\frac{3}{n^2+3}+\cdot + \frac{n}{n^2+n}$$

Ne gândim desigur să folosim "criteriul cleştelui": dacă reuşim să încadrăm şirul între două şiruri convergente la o aceeaşi valoare, atunci şirul este şi el convergent la valoarea respectivă.

De obicei încadrarea unei sume se face înlocuind termenii sumei prin cel mai mic dintre ei şi respectiv prin cel mai mare termen. Făcând diferenţa a doi termeni consecutivi oarecare, deducem imediat că termenii succesivi ai sumei sunt numere ordonate crescător; deci primul termen este cel mai mic, iar ultimul este cel mai mare dintre toţi termenii sumei şi rezultă această încadrare:

$$\frac{n}{n^2+1}\le x_n \le \frac{n^2}{n^2+n}$$

Această încadrare este însă "prea largă": în stânga limita este 0, iar în dreapta limita este 1 (şi nu putem aplica criteriul cleştelui). Putem deduce doar că dacă şirul nostru este convergent, atunci limita este între 0 şi 1. Eşecul la care am ajuns ne arată că ideea obişnuită de încadrare a sumei folosind cel mai mic şi cel mai mare termen, poate să nu fie suficientă.

Până la a continua demersurile matematice necesare pentru a găsi o încadrare "mai fină", putem - şi poate fi mai simplu! - să facem un program prin care să ne dăm seama întâi, care ar fi limita şirului (ştiind rezultatul, putem găsi mai uşor încadrarea necesară). Să ne gândim că vom putea folosi programul şi pentru alte şiruri, când va fi cazul; în plus, vrem ca "programul" respectiv să fie cât mai simplu de folosit (să nu trebuiască să compilăm manual pentru fiecare nou caz, să nu trebuiască să folosim un compilator specific, etc.). Prin urmare este firesc să optăm pentru varianta de a crea o pagină HTML care să conţină scriptul necesar calculării termenilor.

În cadrul documentului HTML ar fi suficient să prevedem următoarele elemente:
— două elemente <input>, pentru a permite utilizatorului să precizeze gama de termeni de calculat (rangul iniţial şi rangul final);
— un element <div> destinat scrierii termenilor şirului, pe măsură ce vor fi calculaţi;
— un <button> a cărui acţionare prin click să declanşeze calculul şi scrierea termenilor respectivi
— un <script> care să modeleze funcţia de calculare a termenilor şirului.

Documentul este furnizat aici: studiu-sir.zip; pentru a investiga un alt şir, trebuie deschis fişierul într-un editor de text şi trebuie rescrisă corespunzător noului şir, funcţia de calculare a termenilor (din cadrul elementul <script> al documentului).

Deschizând din browser documentul nostru, putem obţine de exemplu:

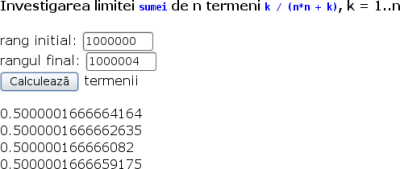
Aceste rezultate ne sugerează că limita şirului ar fi 0.5. Ca să şi dovedim - folosind criteriul cleştelui - ar trebui să reuşim să încadrăm şirul între două şiruri care să aibă fiecare limita 0.5; fiindcă suma numărătorilor fracţiilor din expresia şirului, 1 + 2 + ... + n este n*(n+1)/2 - deducem că trebuie să plecăm de la încadrarea:

$$\frac{k}{n^2+n}\le \frac{k}{n^2+k}\le \frac{k}{n^2+1}$$

Însumând pentru k = 1..n obţinem:

$$\frac{1+2+\cdots + n}{n^2+n}\le x_n \le \frac{1+2+\cdots +n}{n^2+1}$$

Şirurile de încadrare tind ambele la 0.5 şi demonstraţia este încheiată.

Faptul că pentru ranguri de ordinul 10⁶ calculul durează totuşi câteva secunde (cel puţin, pe Firefox) n-ar trebui să surprindă: sunt de făcut 10⁶ împărţiri (şi adunări), ori operaţia de împărţire este cea mai costisitoare (şi ca timp şi ca hardware) dintre toate operaţiile elementare.

Dar uneori sunt posibile diverse optimizări în scopul creşterii vitezei; de exemplu, în funcţia get_sir() (vezi arhiva menţionată mai sus) avem această secvenţă: for(var k = 1; k <= n; k++) suma += k / (n*n + k); în care n*n este calculat ca atare pentru fiecare k = 1..n (şi se ştie că înmulţirea este şi ea, o operaţie costisitoare). Simpla "scoatere în afara ciclului" a operaţiei n*n:

var NN = n * n; for(var k = 1; k <= n; k++) suma += k / (NN + k);

va determina o creştere clară a vitezei de execuţie.