De regulă, Algoritmul lui Dijkstra este formulat cu "tablouri paralele": d[] pentru distanţe şi p[] pentru predecesori; acestea trebuie prevăzute în cadrul programului apelant (la nivel global) - fiind folosite atât în cursul intern al algoritmului, cât şi pentru transmiterea rezultatelor. Unele limbaje permit însă extinderea obiectelor pe parcursul execuţiei (în sensul adăugării de noi proprietăţi) - ceea ce permite integrarea rezultatelor în structura de date transferată algoritmului de către programul apelant (evitând comunicarea prin tablouri suplimentare).
De remarcat că manualele noastre se ocupă de algoritmi (şi de "pseudocod"), nu de programare (scopul fiind sintetizat unilateral prin "formarea unei gândiri algoritmice"); de aceea şi durează ANI mulţi, ca să înveţi să programezi.

Adăugăm nodurilor grafului primit la intrare, proprietăţile "dist" şi "prec". Dacă în varianta obişnuită "defectul" este acela că programul apelant trebuie în prealabil să instituie cele două tablouri d[] şi p[], acum "defectul" ar fi acela că utilizatorul (programul apelant) trebuie informat cumva că va putea folosi rezultatele algoritmului accesând cutare proprietăţi ale nodurilor grafului său (dar accesarea şi exploatarea proprietăţilor asociate obiectelor este un gest elementar subânţeles).

Algoritmul lui Dijkstra determină cele mai scurte drumuri (şi costurile aferente) între un vârf dat şi celelalte vârfuri ale unui graf ponderat pozitiv. În descrierea "pseudocod" următoare folosim notaţiile obişnuite pentru mulţimea vârfurilor, mulţimea muchiilor (sau arcelor) şi funcţia de cost:

algoritm Single-Source-Shortest-Paths_Dijkstra ( graf <V, E; cost>,
                                                nod_start ) 

for_each nod ∈ V { // adaugă proprietăţile .dist şi .prec 
     nod.dist = INFINIT;  // distanţa minimă curentă de la nod_start la nod
     nod.prec = "undefined";  // nodul precedent lui nod pe drumul minim curent
}
nod_start.dist = 0;

Atins = {};  // asociere booleană locală (iniţial vidă), pentru bifarea trecerii printr-un nod:
             // Atins[nod] este definit <==> s-a găsit deja un drum minim până în nod

top = nod_start;  // nodul din care se continuă drumurile, iniţial cel de start
             // la epuizarea posibilităţilor de extindere a drumurilor — când graful 
             // nu este conex, sau când s-au atins toate nodurile — top va deveni "nedefinit"

while( top ) {

     top_adj = lista adiacenţilor neatinşi ai nodului top
               // avem w ∈ top_adj <==> w ∈ V şi NOT Atins[w] şi (top, w) ∈ E

     for_each nod ∈ top_adj { // actualizează nod.dist şi nod.prec
          tmp = top.dist + cost[top][nod]; 
                // = costul prelungirii drumului minim curent cu arcul (top, nod)
          if (nod.dist > tmp) {
               nod.dist = tmp;
               nod.prec = top;
          }
     }

     Atins[top] = 1;  // nodul top nu va mai fi investigat a doua oară
    
     if ( există noduri neatinse tangibile )
          top = nodul neatins care are valoarea .dist minimă
     else
          top = "undefined";

}

Eventual, utilizatorul algoritmului trebuie instruit asupra modalităţii de a exploata rezultatele: drumul minim la un nod al grafului său are costul nod.dist şi poate fi redat (în sens invers) prin iterarea nod = nod.prec, plecând de la arcul (nod.prec, nod).

Obiecte Javascript pentru modelarea grafurilor

În programele cu caracter didactic, "mulţimea vârfurilor" nu există ca obiect: vârfurile sunt vizate în mod implicit prin 1, 2, ..., n (n fiind ordinul grafului) - caz în care modelul de mai sus este inaplicabil. Să renunţăm însă la artificii (pe cât se poate); un graf corespunde eventual unei anumite realităţi şi nodurile—prin ele însele—pot fi importante pentru context (exemplu: graful unei hărţi rutiere - numele localităţilor sunt importante; analog, în aplicaţii web este o obişnuinţă identificarea internă a unor noduri folosind atributul ID din HTML).

Putem reprezenta graful printr-un tablou al nodurilor, unde nod are proprietăţile "nume" şi "adj" şi va putea fi extins cu alte proprietăţi - după următoarea schemă:

function nod() { // constructor de variabile de tip "nod"
    this.nume = '';
    this.adj = [];  // lista adiacenţilor (şi costurilor)
    // alte proprietăţi (necesare eventual în diverşi algoritmi)
};

// exemplu de lucru 
var V = []; // tablou care reprezintă graful prin obiecte nod()
for(var i = 0; i < 5; i++) {
    V[i] = new nod;
    V[i].nume = (i + 1); // aici - obişnuitele "denumiri" 1..n
    V[i].dist = Infinity; // adaugă nodului noi proprietăţi
    V[i].prec = undefined;
}
// adiacenţi, costuri, precedenţi
V[0].adj.push( [V[1], 17], // arcul (V[0], V[1]) de cost 17 
               [V[3], 25] ); // (V[0], V[3]) cost 25
V[1].prec = V[3].prec = V[0]; 

// testare
var tmp = V[0].adj; var str = ' are adiacenţii:\n\t';
for(var i = 0; i < tmp.length; i++) {
    str += tmp[i][0].nume + ', cost = ' + tmp[i][1];
    str += '\tprec: ' + tmp[i][0].prec.nume + '\n\t';
}
alert('vârful ' + V[0].nume + str); 

Acest stil de reprezentare are destule inconveniente; introducerea datelor în program (dar şi gestionarea lor) este greoaie; nodurile sunt accesate indirect, prin V[i]. Mai natural este să reprezentăm nodurile direct prin "nume" (fără a introduce explicit o proprietate .nume cu valori numele respective - cum am făcut mai sus) şi să asociem fiecărui nod (adică fiecărui "nume") tabloul adiacenţilor săi (asociere directă, fără intermedierea unei particule lexicale speciale - cum era mai sus proprietatea .adj).

În JavaScript (şi în alte limbaje) un obiect este o colecţie extensibilă de asocieri de forma CHEIE (unică): VALOARE (orice obiect); ca sintaxă, cheia este separată de valoarea ei prin ":" (iar în Perl, prin "=>"), asocierile respective sunt separate între ele prin virgulă, iar colecţia respectivă este ambalată în acolade. Valoarea corespunzătoare unei chei poate fi accesată folosind cheia drept index (analog accesării elementelor unui tablou). Iar iterarea este asigurată de exemplu prin for( var Cheie in Object ).

Modelăm printr-un asemenea obiect (identificat prin W), graful ponderat alăturat:

var W = {
    'A': [ ['B', 5], ['C', 3], ['E', 2] ],
    'B': [ ['D', 6], ['C', 2] ],
    'C': [ ['B', 1], ['D', 2] ],
    'D': [],
    'E': [ ['B', 6], ['C', 10]
};

W['A'].dist = 0; // nodul de start
W['B'].dist = 4; W['B'].prec = 'C'; 
W['C'].dist = 3; W['C'].prec = 'A';
W['D'].dist = 5; W['D'].prec = 'C';
W['E'].dist = 2; W['E'].prec = 'A';

var str = '';
for(var nod in W) { // după toate cheile 'A', 'B', etc. ale lui W
    str += '\n' + nod + '\tdist = ' + W[nod].dist + '\tprec: ' + W[nod].prec + '\n';
    var adj = W[nod];
    for(var i = 0; i < adj.length; i++)
        str += '\t—> ' + adj[i][0] + '\tcost = ' + adj[i][1] + '\n';
}
alert(str);

Testare (click - vizualizarea datelor grafului de mai sus)

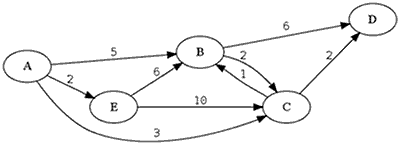
Datele corespund aici tocmai drumurilor minime de sursă 'A'; fiindcă avem W['B'].prec = 'C' şi W['C'].prec = 'A' rezultă că drumul minim la 'B' este 'A'—>'C'—>'B', de cost W['B'].dist = 4.

Această manieră de reprezentare este mult mai convenabilă decât cea indirectă, redată anterior. Ea este folosită mutatis mutandis în diverse alte limbaje sau biblioteci; imaginea de graf reprodusă mai sus a fost obţinută plecând de la un fişier text care descrie graful în limbajul DOT astfel:

digraph {
    rankdir = LR;  // Left-to-Right drawing ( | RL | BT )
    edge [fontname = monospace, fontsize = 12]; // atribute comune pentru 'label'
    A -> E [ label = "2" ]; // arcul (A, E) de cost 2
    A -> B [ label = "5" ];
    A -> C [ label = "3" ];
    B -> D [ label = "6" ];  B -> C [ label = "2" ];
    C -> B [ label = "1" ];  C -> D [ label = "2" ];
    E -> B [ label = "6" ];  E -> C [ label = "10" ];
}

Apelul din linia de comandă dot -Tpng -o dt1.PNG dot-ex.txt a lansat programul dot, care a citit specificaţiile redate mai sus şi a produs fişierul de tip PNG corespunzător imaginii grafului de mai sus.

Pe urmele unei aplicaţii web

Deschidem un editor de text convenabil, sub care vom constitui by hand fişierele necesare aplicaţiei (surse HTML, CSS, JavaScript); creem întâi fişierele agraf.html şi agraf.js, pe care vom lucra concomitent.

Un prim pas - crearea şi corelarea fişierelor de bază

Pentru construirea unui obiect de genul celui indicat mai sus prin var W, să plecăm de la această definiţie:

function Agraph() {
    this.graph = {}; // asocieri Nod : [ [Adiacent1, Cost1], [Adiacent2, Cost2], ... ]
};

pe care o înscriem desigur, în fişierul agraf.js.
Vom putea avea mai multe grafuri (într-o aceeaşi instanţă a browserului), folosind:

  var G1 = new Agraph();  // se creează obiectul G1 în care vom avea graful G1.graph ("vid")
  var G2 = new Agraph();  // şi obiectul G2, unde vom avea graful vid G2.graph

Va trebui să preluăm de undeva datele grafului (noduri, adiacenţe, costuri) şi să le înscriem corespunzător în obiectul .graph propriu instanţei create prin new a obiectului Agraph(). De obicei, pentru asigurarea posibilităţii de a introduce nişte date, se prevede în documentul HTML respectiv un element <textarea>. Pentru început, înscriem în agraf.html:

<script src="agraf.js"></script>

<textarea id="txtGraf-id" rows="10" cols="40"> </textarea>

<script>
    var graf = new Agraph();
</script>

Salvăm cele două fişiere într-un acelaşi director de lucru, fie /home/vb/EXERCITII şi putem face un prim test: deschidem Firefox (sau alt browser) şi tastăm în bara de adresă

(în Firefox apare boxa de text corespunzătoare elementului <textarea>).

Bineînţeles, în acest stadiu agraf.html nu este un document HTML valid; el va trebui completat mai devreme sau mai târziu cu o declaraţie iniţială <!DOCTYPE (poate fi copiată dintr-o sursă HTML existentă) şi desigur cu secţiunile standard <head>, <body>, etc. - după cum este cazul.

În final (după ce va fi publicată), aplicaţia va fi deschisă de către diverşi utilizatori, implicând diverse browsere; trebuie să ne asigurăm că aplicaţia "va merge" pe diverse browsere - aşa că este bine să avem în vedere de la bun început testarea ei în anumite momente, pe mai multe browsere (adaptând după caz, pentru a evita interpretarea diferită a unor specificaţii HTML, CSS sau JavaScript).

Rezumând, am creat fişierul agraf.js în care am definit şablonul de obiect Agraph(); am creat fişierul agraf.html care specifică browserului - prin intermediul atributului src al elementului <script> - să încorporeze (şi eventual să execute) scripturile din agraf.js şi care furnizează o boxă de text - prin intermediul unui element <textarea> - în care se vor putea introduce datele necesare aplicaţiei. Deocamdată (în faza de dezvoltare), aplicaţia se lansează din browserul propriu folosind schema URI file://absolute-path-to-file.

Dedesubturile interacţiunii cu utilizatorul

Utilizatorul va introduce definiţia unui graf ponderat în boxa de text prevăzută în agraf.html, indicând pentru fiecare nod adiacenţii şi costurile aferente; este necesară o funcţie care să preia textul respectiv şi să constituie obiectul .graph după cum am prevăzut în constructorul Agraph().

Totdeauna textul introdus de utilizator trebuie verificat şi eventual "curăţat", înainte de a-l folosi în aplicaţie. Iată un exemplu foarte simplu (dar… din propria experienţă) de situaţie care trebuie evitată: o aplicaţie oferă un tabel în care utilizatorul are de introdus nume şi prenume; trebuie atunci, să ne aşteptăm că vor fi şi utilizatori care - confundând conţinutul cu ambalajul şi vrând să arate ce ştiu ei - vor introduce de exemplu:

<p><FONT SIZE=10 COLOR=RED>POPEXCU</FONT><BR><FONT SIZE=5 COLOR=BLUE>GIORGICA</FONT>

Desigur că informaţia cerută era POPEXCU GIORGICA; deci textul introdus trebuie curăţat în prealabil, de taguri (şi eventual, transformat în Popexcu Giorgica, dacă nu chiar în Popescu Georgică dacă se va putea). Fiindcă veni vorba, repetăm şi noi că taguri ca <FONT> sunt de mult abandonate; valorile atributelor trebuie astăzi încadrate între ghilimele (deci size="10" şi color="red"); obiceiul de a scrie cu majuscule (inclusiv, "facilitatea" CAPS LOCK) este prost din toate punctele de vedere (de exemplu, XHTML nu recunoaşte tagurile formulate cu majuscule; limba literară discalifică şi ea, scrierea cu majuscule a numelor de persoane).

Eliminarea tagurilor sau a altor elemente de text (liniile goale) şi diverse transformări de caractere pot fi realizate relativ simplu folosind expresii regulate; de exemplu var rex = /<([^>]+)>/g; defineşte un şablon de text care corespunde unui tag HTML (începe cu "<", conţine unul sau mai multe caractere exceptând pe ">", se încheie cu ">") şi care are aplicabilitate asupra întregului text (specificatorul final g vine de la "global") - încât o instrucţiune ca myText.replace(rex, ''); va permite eliminarea tuturor tagurilor din myText, păstrând conţinutul propriu-zis (dar aceasta, în ipoteza că tagurile existente sunt corect construite; de exemplu, în textul lui POPEXCU lipseşte la final "</p>" şi atunci conţinutul rezultat va include şi ceea ce urmează eventual după textul respectiv).

Dar pe lângă "curăţirea" textului introdus de utilizator, trebuie totuşi să fie prevăzute diverse formate sub care s-ar putea prezenta datele cerute; de exemplu, introducerea unui vârf şi a listei adiacenţilor săi trebuie permisă şi în formatul A: B-5 C-44.25, dar şi sub forma A : B 5 C 44.25, etc. (în care nodul A are ca adiacenţi nodurile B şi C, costurile arcelor fiind respectiv 5 şi 44.25). Desigur, trebuie să fie posibil şi Iaşi : Vaslui 70 Bârlad 100, dar am putea exclude "Localitatea Iaşi" : "Localitatea Vaslui" 70 (când ar fi necesare ghilimelele, pentru a insera spaţiu în cadrul numelui) - adică am putea pretinde ca firesc, să nu se folosească ghilimele sau apostrof pentru introducerea numelor nodurilor.

Constituirea obiectului de bază

Imitând o exprimare BNF, termenii pe care-i folosim (referindu-ne la textul introdus de utilizator, cât şi la operaţiile de prelucrare a textului) pot fi descrişi sintactic astfel:

<nod, adiacent> :: 
      <secvenţă de caractere alfanumerice> (indicate prin şablonul \w+ (de la "word"))
<cost> :: <cifre zecimale (şablonul \d+)> [<punct (\.)> [<cifre zecimale>]]
<pereche (adiacent, cost)> :: 
      <adiacent> [<spaţii (\s*)>] <separator nealfanumeric (\W)> [<spaţii>] <cost>

Intrăm acum în fişierul agraf.js şi extindem obiectul Agraph() - folosind proprietatea prototype a obiectelor JavaScript - cu o funcţie care să preia textul din boxa de text furnizată de agraf.html şi să o prelucreze corespunzător cu cele de mai sus (definind obiectul .graph din instanţa curentă a obiectului Agraph()); de asemenea, adăugăm o funcţie utilitară care să ne servească pentru verificarea rezultatelor.

function Agraph() {
    this.graph = {}; // asocieri Nod —> [ [Adiacent1, Cost1], [Adiacent2, Cost2], ... ]
};

Agraph.prototype.from_text = function(id_textarea) {
    var str = document.getElementById(id_textarea).value
              .replace(/^\s+/g, '')    /* elimină spaţiile (inclusiv, liniile albe) iniţiale */
              .replace(/\s+$/g, '');   /* elimină spaţiile (inclusiv, liniile albe) finale */

    var arr = str.split(/[\n\r]+/g); // "tabloul rândurilor", cu excluderea rândurilor albe
    // arr[i] conţine datele pentru nodul al i-lea (nume, adiacent, cost, alt_adiacent, cost, etc.)

    var rgx = /\w+\s*\W\s*\d+\.*\d*/g; // va selecta toate perechile (adiacent, cost)
    var rgx1 = /(\w+)\s*\W\s*(\d+\.*\d*)/; // separă adiacentul şi respectiv costul, dintr-o pereche

    for(var i = 0, n = arr.length; i < n; i++) {
        var tmp = arr[i].replace(/^\s+/g, ''); // exclude spaţiile iniţiale din numele adiacentului
        var node = tmp.match(/^\w+/); // numele nodului adiacent nodului al i-lea (alfanumeric)
        var child = arr[i].match(rgx) || []; // = [], dacă arr[i] este "vid" (încât există .length)
        var adj = [];
        for(var j = 0, na = child.length; j < na; j++) {
            var pair = child[j].match(rgx1); // pair[1] = numele nodului adiacent, pair[2] = costul
            adj.push([pair[1], parseFloat(pair[2])]);
        }
        this.graph[node] = adj; // asociază nodului al i-lea, tabloul perechilor [adiacent, cost]
    }
};

Agraph.prototype.dump = function() { // funcţie utilitară - permite afişarea datelor din .graph
    var str = '';
    for(var node in this.graph) {
        str += node;
        var adj = this.graph[node];
        for(var i = 0, n = adj.length; i < n; i++)
            str += '\t-> ' + adj[i][0] + '  ( ' + adj[i][1] + ' )\n';
        str += '\n';
    }
    return str;
};

În funcţia from_text n-am mai "curăţat" textul de eventualele taguri HTML - datorită implicării şablonului \w, orice nume care ar începe cu un caracter ne-alfanumeric (inclusiv tagurile HTML) ar fi ignorat (caracterele < şi > fiind totuşi permise în text ca separator… pentru cazul când utilizatorul ar fi lipsit de inspiraţie).

Pentru o primă testare a lucrurilor, să completăm fişierul agraf.html astfel:

<script src="agraf.js"></script>

<textarea id="txtGraf-id" rows="10" cols="40">
A> B,5 C,3  E - 2
   B< D,6 C,2
C:    B,1    D-6
D
E: B 6 C 10.3    D ,   4
</textarea>

<script>
    var graf = new Agraph();
    graf.from_text("txtGraf-id");
    alert(graf.dump());
</script>

La încărcarea în browser a acestui fişier se va executa scriptul din final, prin care se creează obiectul graf şi se execută metodele componente from_text şi dump, alertând în final rezultatele prelucrării datelor deja înscrise în scop de testare, în elementul <textarea>: Testare (sub Firefox).

De la pseudocod la metodă

Până să abordăm şi chestiunea mai pretenţioasă a vizualizării paşilor principali (cum ne propusesem) - să vedem şi cât este de adecvat obiectul Agraph(), pentru a permite o "traducere" uşoară a pseudocodului formulat la început pentru algoritmul lui Dijkstra:

Agraph.prototype.sssp_dijkstra = function(start ) {
    var graf = this.graph; // scurtează accesarea datelor din obiect (reduce indirectările)
    var atins = {};
    for(var nod in graf) { // individualizează şi iniţializează .dist şi .prec
        graf[nod].dist = Number.MAX_VALUE; 
        graf[nod].prec = undefined;
    }
    graf[start].dist = 0;
    var top = start;
    while(top) {
        atins[top] = 1; // drumul minim până la top a fost găsit
        var top_adj = []; // lista adiacenţilor lui top neatinşi la momentul curent
        for(var i = 0, n = graf[top].length; i < n; i++) {
            var pair = graf[top][i]; // referă tabloul [adiacent, cost]
            if(!atins[pair[0]])
               top_adj.push(pair);
        }
        for(var top_dist = graf[top].dist, i = 0, n = top_adj.length; i < n; i++) {
            var adj = top_adj[i];
            var nod = graf[adj[0]]; // referinţă care scurtează accesul la .dist şi .prec
            var tmp_dist = top_dist + adj[1];
            if(nod.dist > tmp_dist) { // trecând prin top, se ajunge mai uşor la nod
                nod.dist = tmp_dist;
                nod.prec = top; // drumul minim spre nod trece prin top
            }
        }
        var cand = undefined; // candidat pentru extindere (dacă se va găsi unul) 
        var mind = Number.MAX_VALUE; // se caută nodul neatins cu .dist minimă
        for(var nod in graf) {
            if(!atins[nod] && graf[nod].dist < mind) {
                cand = nod; // s-a găsit un candidat mai bun
                mind = graf[nod].dist;
            }
        }
        top = cand; // nodul din care urmează să se extindă drumurile (dacă există); 
    }
};

Ar fi acum de adăugat obiectului Agraf() o metodă prin care să se furnizeze drumul (rezultat prin invocarea metodei de mai sus) până la un nod precizat. Deocamdată, numai pentru testare - putem folosi o funcţie independentă care primind o referinţă la obiectul graph dintr-o instanţă Agraph(), returnează un şir conţinând toate drumurile minime dintr-un acelaşi nod:

function dump_sssp(graf) { // referinţă la obiectul .graph dintr-o instanţă de Agraph() 
    var str = ''; // toate drumurile minime dintr-un acelaşi punct, separate prin '\n'
    for(var nod in graf) {
        if(graf[nod].dist < Number.MAX_VALUE) { // nodurile la care s-a putut ajunge
            var arr = []; // tabloul nodurilor intermediare (iniţial - în sens invers)
            arr.push(nod);
            var prec = graf[nod].prec;
            while(prec) { // nodul de start are prec==undefined şi dist==0
                arr.push(prec);
                prec = graf[prec].prec;
            }
            // reprezentarea drumului, în sens direct (şi costul aferent)
            str += arr.reverse().join(' —> ') + '\t(costă ' + graf[nod].dist + ')\n';
        }
    }
    return(str);
};

În această funcţie am folosit '\n' pentru a separa drumurile între ele (în cadrul şirului str), intenţionând să folosim alert() (care cel puţin în Firefox, interpretează în modul standard caracterul '\n'); însă dacă ar fi fost să "afişăm" str într-o diviziune a documentului, atunci trebuia să folosim '<br>' în loc de '\n'.

Testarea se va realiza lansând agraf.html, dar după ce în prealabil, vom fi completat <script>-ul final astfel:

<script>
    var graf = new Agraph();      // instanţă de obiect Agraph()
    graf.from_text("txtGraf-id"); // constituie obiectul graf.graph
    // alert(graf.dump()); 
    graf.sssp_dijkstra('A');      // proprietăţile .dist şi .prec (faţă de 'A') ale nodurilor
    alert(dump_sssp(graf.graph)); // şirurile reprezentând drumurile minime (şi costurile minime)
</script>

Cu aceasta, încheiem o primă etapă de dezvoltare a aplicaţiei… Ne propusesem "chestiunea mai pretenţioasă a vizualizării paşilor principali" - dar un asemenea scop ţine mai degrabă de ironie!

În manuale se obişnuieşte ca după ce se formulează un algoritm, acesta să fie clarificat pas cu pas (de exemplu, pe un graf cu 5 vârfuri), prin desene şi tabele de valori intermediare; şi cam aşa face oricine - dar, cu creionul propriu - ca să înţeleagă "la prima citire" un algoritm.

Dar acest obicei - practicat abuziv în manuale şi la clasă pentru fiecare algoritm - are (în lipsa altor îndrumări) şi un efect pervers, nedorit. Începătorul se obişnuieşte să "testeze" orice program pe care-l face pe date de genul n = 5; până la urmă, concluzia lui ar putea fi că la asta "serveşte" calculatorul şi algoritmii: să calculeze factorial de 3, să afişeze drumurile într-un graf cu 5 vârfuri, sau să spună dacă numărul 97 este prim (şi altfel, serveşte cum ştie toată lumea bună, pentru filme, poze şi muzică, pentru chat-uri şi desigur, pentru a scrie cu Word - în fond, repetând în plan modern binecunoscuta etapă a dezvoltării noastre: "La Paris ai noştri tineri...").

În loc de a prefabrica mereu vizualizări ale desfăşurării algoritmului, ar fi mult mai util să se vizeze formarea deprinderii elementare de a folosi propriul creion şi propriile date şi de asemenea, formarea deprinderii de a utiliza instrumente specifice de trasare a execuţiei programului (care ar permite desigur şi "vizualizarea" paşilor algoritmului din manual). Iar în cazul aplicaţiei noastre (şi în general, pentru aplicaţii web), urmărirea paşilor algoritmului se poate face folosind de exemplu, Firebug.

Elementele client-server ale aplicaţiei

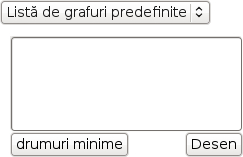
Aplicaţia ar expune patru elemente de interacţiune.

Un <select> permite alegerea unui graf dintr-un tablou predefinit şi afişează datele acestuia în elementul <textarea> (unde utilizatorul poate înscrie direct şi propriul său graf).

<button>-ul drumuri minime asigură crearea unui obiect Agraph() corespunzător datelor înscrise în <textarea> şi invocă metoda pentru obţinerea drumurilor minime, înscriind rezultatul într-o anumită diviziune a documentului.

Acţiunile menţionate mai sus se desfăşoară la nivelul client, în browserul propriu. <button>-ul Desen asigură transmiterea către server a datelor grafului; un anumit modul (Perl de exemplu) de pe server primeşte aceste date şi le transpune într-un format grafic, care este apoi returnat browserului.

Imaginea următoare evocă o traducere în realitate, a schiţei descrise:

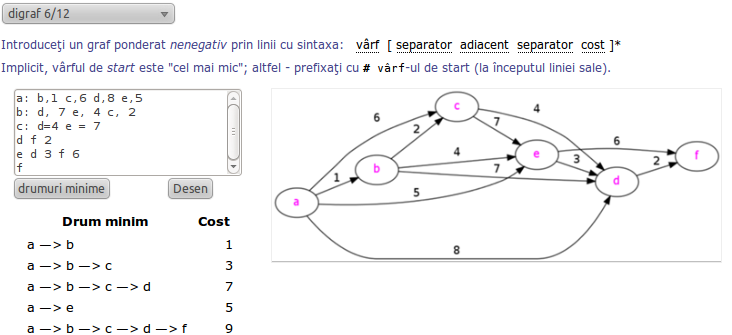
De la obiect JavaScript la şir JSON

În JavaScript, obiectele sunt pasate prin referinţă (nu "prin valoare") şi nu pot fi transmise spre exterior (unui program de pe server) ca atare, ci doar prin intermediul unei operaţii de serializare - prin care valorile (datele propriu-zise, din obiect) sunt concatenate într-un anumit format text; textul rezultat poate fi transmis spre exterior (serverului, de către browser), unde el urmează să fie interpretat corespunzător.

Serializarea implică eventual şi câteva convenţii prealabile privind tipul datelor de transmis, încât programul receptor (într-un alt limbaj, de obicei) să poată restructura intern datele respective; de exemplu, pentru a transmite un tablou, elementele lui trebuie ambalate în text cu caracterele '[' şi ']'; sau dacă este vorba de un obiect JavaScript, atunci se convine ca asocierile conţinute să fie scrise în text între acolade.

De obicei, se alege un format standardizat de reprezentare externă, încât textul respectiv să poată fi "decodificat" uşor (adică, fără a fi necesar un program propriu pentru aceasta); de exemplu, pentru formatul JSON (JavaScript Object Notation) există programe standardizate (pentru serializare şi deserializare) în multe dintre limbajele folosite la un capăt sau la capătul celălalt, al comunicării între browser şi server.

Un mic experiment poate arăta diferenţa dintre obiect JavaScript şi formatul serializat al acestuia:

var elev = { "nume": "Ionescu", "pren": "Mihai", "note": [ [9, 9, 10], [8, 8] ] };
alert(elev); //  [object Object]
alert(elev.nume + ' ' + elev.pren + ' ' + elev.note); //  Ionescu Mihai 9,9,10,8,8 
alert(Object.toJSON(elev)); //  {"nume": "Ionescu", "pren": "Mihai", "note": [[9, 9, 10], [8, 8]]}

S-a creat un obiect cu proprietăţile nume, pren şi note. Variabila elev este o referinţă la acest obiect şi este pasată funcţiei alert(), rezultând mesajul [object Object]. Al doilea alert() afişează valorile proprietăţilor obiectului referit prin elev (angajând datele propriu-zise, fără a ţine seama de aspecte structurale, de exemplu de faptul că datele asociate proprietăţii note constituie "un tablou de tablouri").

În al treilea alert(), Object este un namespace (nu are de-a face cu constructorul Object(), predefinit în JavaScript şi folosit sub forma var obj = new Object()), introdus de biblioteca prototype.js şi care include şi metoda toJSON(); rezultatul produs este "şirul JSON" a obiectului referit de elev. Aparent, şirul JSON obţinut este identic definiţiei la nivel de sursă-program, a obiectului atribuit variabilei elev; dar să evităm confuzia: şirul JSON este realmente un "şir de caractere" furnizat ca atare, în timp ce definiţia la nivelul sursei programului nu există ca "şir de caractere" în codul compilat, ci a servit numai la compilarea textului sursă, pentru a se crea în memorie obiectul respectiv (împreună cu "pointerii" specifici, vizibili sau "ascunşi").

În cazul aplicaţiei noastre, datele au o structură relativ simplă - încât putem evita implicarea vreunei biblioteci precum prototype.js (care oferă mult mai mult decât am avea nevoie aici). Extindem obiectul Agraph() cu o metodă care returnează şirul JSON corespunzător obiectului intern graph:

Agraph.prototype.to_json = function() {
    var json = '';
    for(var node in this.graph) {
        json += '"' + node + '":['; // urmează lista adiacenţilor nodului curent
        var adj = this.graph[node], n = adj.length - 1;
        for(var i = 0; i < n; i++) // tratează adiacenţii, exceptând pe ultimul
            json += '["' + adj[i][0] + '",' + adj[i][1] + '],';
        if(n >= 0) // ultimul adiacent e tratat separat pentru a evita virgula finală
            json += '["' + adj[n][0] + '",' + adj[n][1] + ']';
        json += '],'; // încheie pentru nodul curent, lista adiacenţilor
    }
    return '{' + json.replace(/,$/, '') + '}'; // după eliminarea virgulei finale
};

Pentru testare:

    var graf = new Agraph();
    graf.from_text ('txtGraf-id');
    alert ( graf.to_json() ); 

cu rezultat precum: {"A":[["B",5],["C",3],["E",2]],"B":[["D",6],["C",2]],"C":[["B",1],["D",2]],"D":[],"E":[["B",6],["C",10]]}. Am evitat spaţiul, în şirul JSON returnat: de exemplu, n-am adăugat '], ' (patru caractere), ci '],' (trei caractere); justificarea economisirii decurge din restricţionările existente asupra lungimii maxime a Query-string-urilor.

De la şir JSON la variabilă Perl

Să presupunem că browserul a transmis serverului un şir JSON, corespunzător unui obiect JavaScript, iar acest şir este pasat unui program Perl care are de făcut anumite prelucrări asupra datelor primite (urmând să returneze un anumit rezultat pe care serverul să-l transmită înapoi browserului de la care a primit datele).

În cazul nostru de exemplu, un browser trimite şirul JSON corespunzător obiectului Agraph(); programul Perl trebuie să-şi constituie variabilele proprii, conform specificaţiilor existente în şirul JSON primit şi să le folosească în modul specific, pentru a putea furniza ca rezultat o imagine grafică a grafului respectiv.

Desigur, mai întâi (până a ne ocupa chiar de acel program Perl necesar aplicaţiei noastre) imaginăm un mic program independent, de simulare şi testare a lucrurilor:

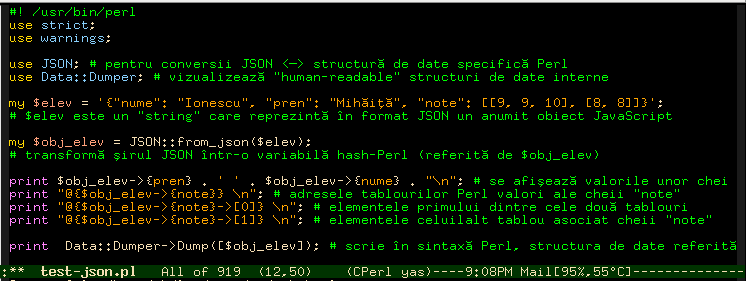
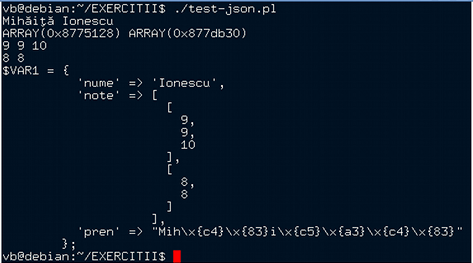
Rezultatele execuţiei atestă că prin JSON::from_json($elev), Perl a convertit şirul JSON primit într-o variabilă internă (o referinţă la o zonă de memorie structurată ca hash); metoda Data::Dumper->Dump() apelată în final, a serializat în formă human-readable (sub sigiliul $VAR1) conţinutul memoriei referite prin variabila creată.

Obţinerea unei imagini a grafului

Să presupunem acum că programul Perl existent pe server a primit şirul JSON corespunzător unui Agraph() şi l-a convertit în variabilă Perl proprie; urmează să implice un anumit modul care să convertească datele respective într-o imagine grafică a grafului.

Iarăşi, imaginăm întâi un program de sine stătător, pentru simularea şi testarea lucrurilor:

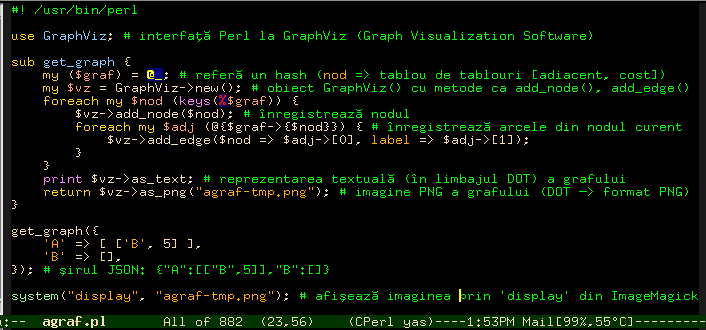
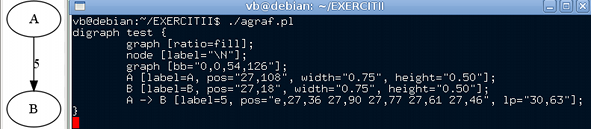
Am folosit modulul GraphViz, care permite accesarea din Perl a unor programe din Graphviz - Graph Visualization Software; aceste programe presupun ca intrare o descriere textuală (în limbajul DOT) a unui graf şi produc la ieşire "diagrame" în diverse formate (de exemplu, ca fişier sau imagine PNG).

Să observăm că puteam evita crearea fişierului temporar agraf-tmp.png, încheind get_graph() prin return $vz->as_png(), eliminând din final comanda system() şi apelând programul astfel: ./agraf.pl | display (PNG-ul rezultat este transmis direct programului display, fără intermediul unui fişier propriu-zis).

Controller-ul final

Presupunând că pe server se foloseşte Catalyst, putem formula următorul modul Perl - o schemă totuşi, a unuia "real" - în care înglobăm experienţa celor două programe Perl concepute mai sus:

package MyApp::Controller::Agraph;
use base 'Catalyst::Controller';
use GraphViz;
use JSON;

sub _do_get_graph { # subrutină privată, apelată numai prin get_graph()
    # realizează intern descrierea DOT a unui graf (hash Perl)
    # şi returnează formatul PNG corespunzător acesteia
    my ($g) = @_; # primeşte o referinţă la graf
    my $vz = GraphViz->new(
        rankdir => 1,
        edge => {fontname => 'monospace'},
        node => {fontname => 'Verdana', fontcolor => 'magenta'},
    );
    foreach my $nod (keys(%$g)) { # accesează cheile hash-ului referit de $g
        $vz->add_node($nod);
        foreach my $adj (@{$g->{$nod}}) {
            $vz->add_edge($nod => $adj->[0], label => $adj->[1]);
        }
    }
    return $vz->as_png; 
}

sub get_graph : Local { # va deservi cereri /agraph/get_graph?graph=
    my ($self, $c) = @_;
    my $graph = $c->request->param('graph'); # şirul JSON de intrare

    $graph = JSON::from_json($graph); # variabile Perl corespunzător şirului JSON
    
    my $png = _do_get_graph($graph); # descrierea DOT a grafului şi apoi imagine PNG

    $c->response->headers->header( 'Content-Type', 'image/png' );
    $c->response->body($png); # browserul va primi PNG-ul grafului
}

1;

Acest modul (odată integrat prin Catalyst) va putea deservi cereri de genul /agraph/get_graph?graph={"a":[["b",10],["c",5]]}, formulate de un browser fie direct (prin bara de adresă), fie prin intermediul unui eveniment onclick() ataşat (printr-o funcţie JavaScript) unui <button> din documentul curent. Următoarele rezultate (obţinute accesând log-urile produse de Apache) arată cum decurge o astfel de cerere:

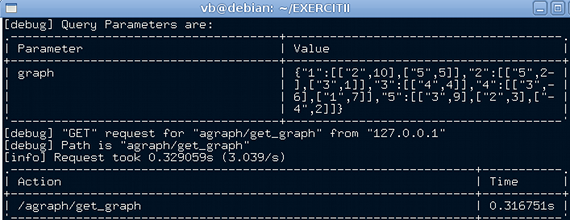
În cazul de faţă, la originea cererii a fost click-ul pe butonul Desen al aplicaţiei noastre (după ce în prealabil, s-a selectat unul dintre grafurile predefinite existente). Desigur, aici am implicat serverul "local" 127.0.0.1 şi nu serverul pe care ar fi publicată aplicaţia (pe un server real, opţiunea debug din Catalyst trebuie fireşte, dezactivată).