De regulă, manualele şcolare introduc "numerele complexe" plecând de la "x²+1=0"; dar istoria ne dezvăluie că inventarea şi instrumentarea numerelor complexe nu este legată de "ecuaţia de gradul doi", ci se datorează eforturilor de rezolvare a ecuaţiei cubice. Am evidenţiat în [1] unele dintre aceste demersuri, arătând şi că formula trigonometrică exprimată de François Viète pentru rădăcini reale distincte este valabilă de fapt pentru oricare caz (inclusiv pentru coeficienţi complecşi), dacă în formula respectivă se consideră cos() ca funcţie de variabilă complexă.

Bazându-ne pe această formulă trigonometrică, am evidenţiat unele proprietăţi geometrice ale rădăcinilor: în cazul vizat de Viète, ele sunt proiecţiile reale din rădăcinile de ordinul trei ale unităţii, după o anumită rotire şi scalare; pentru cazul când toate sunt complexe (nereale), tot formula lui Viète ne-a condus la teorema lui Marden: punctele critice sunt focarele elipsei Steiner înscrise triunghiului rădăcinilor (elipsa tangentă laturilor în mijloace, centrată în baricentru).

Experimentând grafic în R, am ajuns în [1] să formulez şi două-trei chestiuni inedite - dintre care una am clarificat-o: locul valorilor parametrului complex p al ecuaţiei z³ + pz + q = 0, z ∈ C, când două rădăcini - una fixată, cealaltă mobilă - se află pe cercul unitate, este o trisectoare Pascal. Avem şi o reformulare simplificată (ca "problemă propusă"), aparent nelegată de ecuaţia de gradul trei: care este locul geometric al punctului de afix z(z+1), când |z|=1?

Lămurim acum şi problema locului punctelor critice (în condiţiile menţionate, pentru rădăcini).

Considerăm polinomul $f(z)=z^3+pz+q,\,z\in\mathbb{C}$, cu $p,q\in\mathbb{C}$; suma rădăcinilor este $0$ (din relaţiile lui Viète). Presupunem că două rădăcini - una fixă $z_1$ şi una mobilă, $z_2$ - se află pe un acelaşi cerc, centrat în origine; care este atunci, locul punctelor critice ale lui $f$?

Punctele critice sunt rădăcinile derivatei $f'(z)=3z^2+p$; fiindcă $f'(-z)=f'(z)$ (iar punctele de afixe $z$ şi $-z$ sunt simetrice faţă de originea sistemului de axe), avem imediat că locul căutat - pe care îl notăm cu $\mathcal{H}$ - este o curbă simetrică faţă de origine. Vedem deasemenea imediat, că $\mathcal{H}$ este în fond transformata prin funcţia complexă sqrt() a curbei descrise de valorile coeficientului $p$ (fiindcă $f'(z)=0 \rightarrow z^2=-p/3$); adică - ţinând seama de cele stabilite în [1] - putem spune că $\mathcal{H}$ este radicalul trisectoarei lui Pascal.

Rotaţia cu un anumit unghi în jurul originii şi scalarea cu un anumit factor nu modifică forma curbei - încât putem considera că cercul fixat este cercul de rază $1$ centrat în origine, iar rădăcina fixă este $z_1=1$; această simplificare uşurează stabilirea ecuaţiilor curbei (pe baza cărora vom reuşi să încadrăm $\mathcal{H}$ într-o anumită familie de curbe).

Avem $p=z_1z_2+z_1z_3+z_2z_3$ şi cum $z_1=1$ şi $z_3=-1-z_2$, obţinem $p=-(z_2^2+z_2+1)$; punând $z_2=e^{i\theta}$ (rădăcina mobilă), avem o ecuaţie parametrică a curbei descrise de $p$: $$p(\theta)=-(e^{2i\theta}+e^{i\theta}+1),\,\theta\in[0,2\pi]$$

recunoscută în [1] ca fiind o trisectoare Pascal. Ecuaţia lui $\mathcal{H}$ este $w(\theta)=\small\pm\sqrt{1/3\,}\sqrt{-p(\theta)\,}$ sau, ignorând factorul de scalare: $$w(\theta)=\pm\sqrt{e^{2i\theta}+e^{i\theta}+1\,},\,\theta\in[0,2\pi]$$

Însemnând părţile lui $w(\theta)$ - reală şi respectiv, imaginară - cu $x$ şi $y$ (omiţând în această notaţie, parametrul $\theta$ al acestora), obţinem (prin ridicare la pătrat şi separarea părţilor): $$\array{\cos 2\theta+\cos\theta&=&x^2-y^2-1\cr\sin 2\theta+\sin\theta&=&2xy}$$

Însumând membru cu membru pătratele acestor două egalităţi, găsim:$$\cos\theta=\frac{1}{2}\left((x^2-y^2-1)^2+4x^2y^2-2\right)$$

şi înlocuind astfel $\cos\theta$ în prima egalitate de mai sus, obţinem "ecuaţia carteziană" a lui $\mathcal{H}$:$$\left((x^2+y^2)^2-2(x^2-y^2)\right)^2-(x^2+y^2)^2=0$$

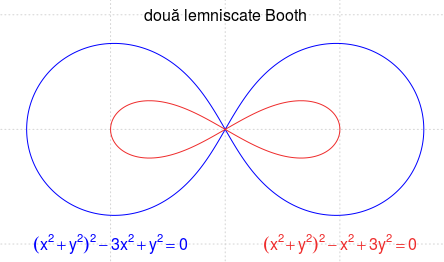
sau, descompunând diferenţa de pătrate:$$\boxed{\left((x^2+y^2)^2-3x^2+y^2\right)\left((x^2+y^2)^2-x^2+3y^2\right)=0}$$

Prin urmare, $\mathcal{H}$ reuneşte două lemniscate Booth (cu acelaşi centru şi aceleaşi axe) - curbe cu ecuaţia generală $(x^2+y^2)^2=cx^2+dy^2$, care pentru $d \lt 0$ (ca în cazul nostru) seamănă cu simbolul grafic "∞" (iar pentru $d=-c$ am regăsi lemniscate Bernoulli).

Graficul unei ecuaţii implicite de două variabile se poate produce în R, folosind contour() - funcţie care asigură (mai general decât avem nevoie aici) vizualizarea curbelor de nivel ale unei suprafeţe; următoarea funcţie primeşte ca argument funcţia "func2" (pentru care vrem să vizualizăm curbe de nivel) şi o invocă prin outer(), obţinând vectorul înălţimilor corespunzătoare punctelor (x, y), iar în final conturează curbele de nivel respective:

plot_oval <- function(func2, ...) {
  x <- y <- seq(-2, 2, by=0.001)  # constituie o reţea de puncte
  levels <- 0  # <- c(0, 0.5, 1) ## mai multe curbe de nivel
  Z <- outer(x, y, func2)  # înălţimea în fiecare punct al reţelei
  contour(x, y, Z, levels = levels, drawlabels=FALSE, ...)
}

Argumentul "..." permite transmiterea către contour(...) a unor parametri grafici (de exemplu, culoarea de trasare a curbelor). Prin plot_oval() putem obţine acum graficul curbei $\mathcal{H}$ astfel:

plot(0, type="n", xlim=c(-2, 2), ylim=c(-2, 2), asp=1); grid()
plot_oval(function(x, y) (x^2+y^2)^2 - 3*x^2 + y^2, col="blue")
plot_oval(function(x, y) (x^2+y^2)^2 - x^2 + 3*y^2, add=TRUE, col="firebrick2")

Este interesant să revedem cazul "general", când rădăcina fixă este $z_1=e^{i\alpha}$ (în loc de $z_1=1$), cu $\alpha$ ales arbitrar; cu ce unghi trebuie rotit planul, pentru ca din curbele descrise de parametrul $p$ şi de punctele critice corespunzătoare cazului "simplificat" tratat mai sus, să regăsim pe cele care ar fi asociate cazului "general"? Prin programul următor atestăm că acest unghi este $2\alpha$ (dublul argumentului rădăcinii fixate).

Procedăm astfel: fixăm aleatoriu $z_1=e^{i\alpha}$ şi trasăm prin linie "continuă" curbele cazului general, angajând direct expresiile $p=z_1z_2+z_1z_3+z_2z_3$ şi $\delta=\pm\sqrt{-p/3\,}\,$ (cu observaţia că $p$ se poate rescrie ca $p=-(C^2+z_1C+z_1^2)$, unde $C=e^{i\theta}$ este punctul mobil $z_2$); apoi, trasăm prin puncte mai rare (pentru lizibilitate) curbele rezultate prin rotirea cu unghiul $2\alpha$ a curbelor asociate cazului simplificat, descrise mai sus prin ecuaţiile parametrice pentru $p(\theta)$ şi $w(\theta)$. Dacă avem dreptate, curbele continue şi cele punctate trebuie să se suprapună.

t <- seq(0, 2*pi, length=2000)
C <- exp(1i*t)  # cercul unitate (eşantion de 2000 puncte) 
z1 <- sample(C, 1)  # fixează aleatoriu rădăcina z1
plot(0, type="n", xlim=c(-3, 3), ylim=c(-3, 3), asp=1, 
     xlab="", ylab="", xaxt="n", yaxt="n", bty="n")  # pregăteşte fereastra grafică
points(z1, cex=0.7)  # marchează rădăcina fixă
p <- -(C^2 + z1*C + z1^2)  # exprimat direct din polinomul z^3 + pz + q
delta <- sqrt(-p/3)  # punctele critice (3z^2 + p = 0)
points(p, type="l", col="red")  # trisectoare Pascal
points(c(delta, -delta), type="p", col="green", cex=0.01)  # lemniscate Booth

p1 <- function(u) {  # se angajează p(θ) din ecuaţia parametrică "simplificată"
  p <- function(u) -(exp(2i*u) + exp(1i*u) + 1)  
  Mod(p(u)) * exp(1i*(Arg(p(u)) + 2*Arg(z1)))  # roteşte p(θ) cu 2*Arg(z1)
}
t1 <- seq(0, 2*pi, by=0.1)  # puncte mai rare decât cele din vectorul 't'
booth <- 1/sqrt(3) * sqrt(-p1(t1))
points(p1(t1), type="p", col="black", cex=0.01)  # punctează trisectoarea
points(c(booth, -booth), type="p", col="black", cex=0.01)  # punctează lemniscatele

Pentru $f(z)=z^3+pz+q,\,z\in\mathbb{C},\,(p,q\in\mathbb{C})$ cu două rădăcini de modul $1$, una fixată şi una mobilă:

locul valorilor $p$ este o trisectoare Pascal (curba roşie), iar locul punctelor critice este reuniunea a două lemniscate Booth (marcate cu verde).

Subliniem că pentru a "efectua" rotaţia (în corpul funcţiei notate cu "p1()" în programul de mai sus), a trebuit să determinăm vectorul modulelor şi vectorul argumentelor punctelor $p(\theta)$ (căci $\theta$ nu este "unghiul polar", ci doar parametrizează un interval de lungime $2\pi$).