Formulele matematice sunt scrise folosind MathJax; click-dreapta pe una dintre ele şi alege Math Settings / Math Renderer / SVG (pentru cea mai bună vizualizare, dependent de browser-ul folosit).

Identitatea $(u+v)^3-3uv\,(u+v)-(u^3+v^3)=0$ leagă ecuaţia redusă de gradul trei

$f(x)=x^3+p\,x+q=0\hskip5em \small(1)$

de rezolvarea sistemului (ori discuţia condiţiilor)

$-3uv=p, \,\,\, -(u^3+v^3)=q\hskip5em \small(2)$

Legătura $x=u+v$ între acestea, pleacă probabil de la faptul că rădăcinile ecuaţiei (1) au suma zero (coeficientul lui $x^2$ fiind $0$) - deci una dintre ele se opune sumei celorlalte două.

În vederea aplicării acestei idei, ecuaţia generală $g(x)=x^3+ax^2+bx+c=0$ se poate reduce, printr-o anumită translaţie $x\rightarrow x+h$: dacă $x_1,x_2,x_3$ sunt rădăcinile lui $g(x)$, atunci (din relaţiile lui Viète) avem $x_1+x_2+x_3=-a$; rădăcinile lui $g(h-x)$ vor fi $h - x_i\,\,{\small (i=1..3)}$ şi au suma $3h+ a$ care devine zero (conducând la forma "redusă") pentru $h=-a/3$.

Acest procedeu - eminamente algebric - a fost inventat înainte de 1550 de către matematicieni italieni (del Ferro, Tartaglia, Cardano); pe atunci se lucra numai cu numere "reale" (mai ales, cu numere pozitive) şi a fost chiar stresant faptul că exprimarea soluţiilor reale angaja inevitabil valoarea "inexistentă" $\sqrt{-1}$ (este de subliniat că inventarea şi instrumentarea numerelor complexe nu este legată de "ecuaţia de gradul doi", ci se datorează eforturilor de rezolvare a ecuaţiei cubice). Iar legarea ecuaţiei de analiza funcţiei asociate (monotonie, puncte critice, aproximări) s-a putut face după încă vreo 150 de ani - când Newton şi Leibniz au fundamentat "calculul diferenţial şi integral", iar Descartes şi alţii au imaginat studiul sistematic al curbelor asociate ecuaţiilor (constituind "geometria analitică").

Primele derivate ale funcţiei $g(x)$ sunt: $g'(x)=3x^2+2ax+b$ şi $g''(x)=2(3x+a)$. Vedem acum că $h=-a/3$ este de fapt rădăcina lui $g''(x)$ - deci este punctul de inflexiune al graficului (considerând că $a,b,c \in \mathbb{R}$).
Valorile asociate primelor două derivate determină complet natura (şi eventual, construcţia) rădăcinilor ecuaţiei cubice. Este suficient să considerăm forma redusă (1), cu $p, q\in \mathbb{R^*}$.

Punctul de inflexiune $(0,q)$ este centrul de simetrie al curbei $y=f(x)$; într-adevăr, avem $f(x)+f(-x)=2q$ - deci punctele $\small (x,f(x))$ şi $\small (-x,f(-x))$ sunt simetrice faţă de $\small (0,q)$.

Avem $f'(x)=3x^2+p$. Dacă $p\gt 0$, atunci $f'\gt 0$ deci $f$ este funcţie strict crescătoare, încât în acest caz avem o singură rădăcină reală $\lambda$, de semn contrar lui $q$ (când punctul de inflexiune $(0,q)$ este deasupra axei $y=0$ şi numai atunci, $\lambda \lt 0$). Putem determina această rădăcină, căutând $u$ şi $v$ care satisfac condiţiile (2) - atunci $x=u+v$ va fi rădăcina reală $\lambda$; să observăm că $u=\sqrt[3]{-q/2+\small \Delta}$ şi $v=\sqrt[3]{-q/2-\small \Delta}$ (cu $\small \Delta$ arbitrar) satisfac deja $u^3+v^3=-q$; valoarea parametrului $\Delta$ o găsim din prima condiţie, $3uv=-p$ şi obţinem $\Delta ^2=q^2/4+p^3/27$ (care este pozitiv, fiindcă $p\gt 0$ - deci îi putem calcula radicalul, implicat în expresiile lui $u$ şi $v$).

Ilustrăm cazul $p\gt 0$ alegând $p=4.5$ şi variind $q$ (punctul roşu) într-un interval centrat în zero:

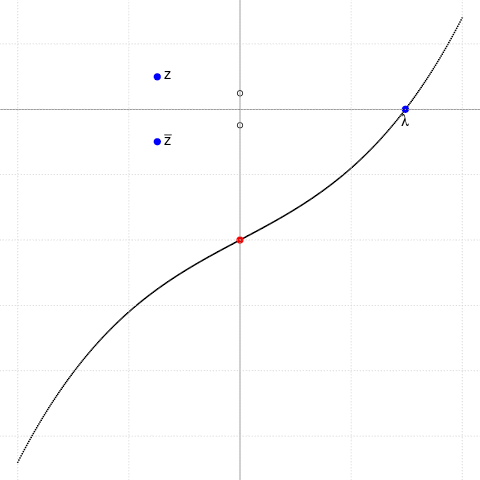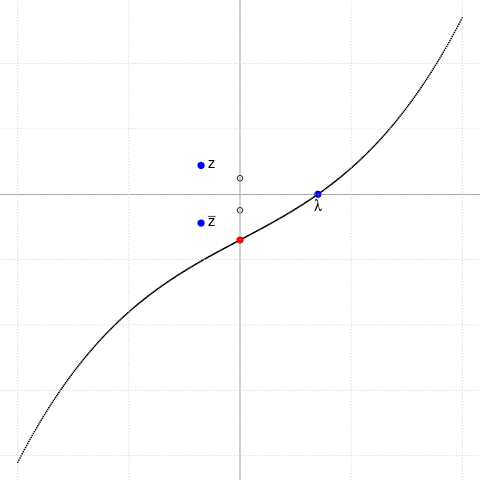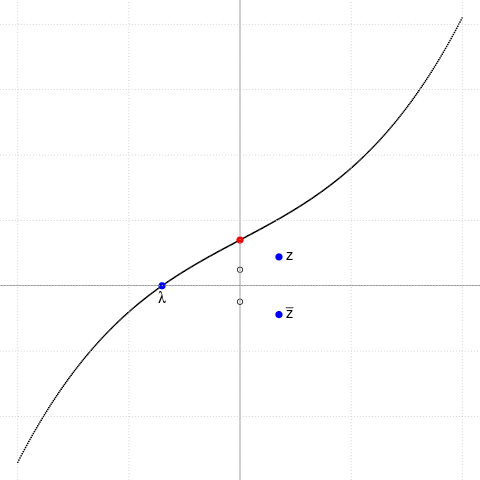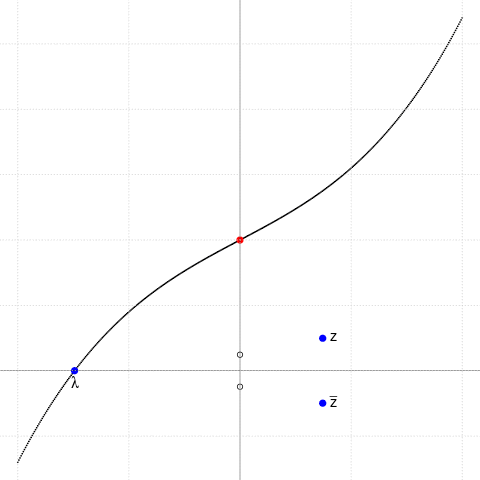
$f(x)=x^3+px+q,\,\,\,p=\small 4.5$
($p\gt 0$: avem o singură rădăcină reală, $\lambda$)

$q=\small -10+k*0.5,\,\,k=0..40$
(punctul roşu $(0,q)$ este punctul de inflexiune)

$\lambda=\sqrt[3]{\Delta-q/2}-\sqrt[3]{\Delta+q/2}$,
unde $\Delta^2=q^2/4+p^3/27$ (este $\gt 0$, fiindcă $p\gt 0$)

Pentru rădăcinile complexe (conjugate), avem:
$z+\bar{z}=-\lambda$ şi (fiindcă produsul rădăcinilor = $-q$)
$z\bar{z}=\frac{-q}{\lambda}=\frac{\lambda^3+\,p\lambda}{\lambda}=\lambda^2+p$

Imaginea redată mai sus este animată (deschide-o într-un "Tab" nou şi foloseşte combinaţia de taste "CTRL + R"); realizarea ei implică alte "legături": am constituit un program R prin care am plotat $y=f(x)$ pentru fiecare valoare a parametrului $q$ - salvând de fiecare dată în câte un fişier; în final, din fişierele ".png" rezultate am obţinut un "GIF animat" folosind programul convert() din pachetul ImageMagick: convert -delay 4 -loop 1 *.png cubic1.gif".

Precizăm totuşi, că unităţile de măsură pentru axe diferă şi că am procedat "ca programatoru' ", folosind câte un plot() pentru fiecare $q$; de fapt, era suficient să plotăm efectiv doar $y=x^3+px$ şi să deplasăm pe verticală (cu pasul $q$) doar axa absciselor - cum a rezultat în final, pe animaţie ("de fapt"… nu era suficient: cadrele animaţiei provin din fişiere independente şi fiecare cadru trebuie să conţină şi graficul funcţiei).

Mai sus, am ajuns la discriminantul $\Delta^2$ prin calcul direct; arătăm acum că expresia respectivă rezultă şi plecând de la "punctele critice". Fie $\pm\delta$ rădăcinile ecuaţiei $f'(x)=3x^2+p=0$ (sunt simetrice faţă de origine, pe axa imaginară dacă $p\gt 0$, respectiv pe axa reală dacă $p\lt 0$); deci $p=-3\delta^2$ şi avem $f(\delta)=\delta^3+p\delta+q=q-2\delta^3$, iar $f(-\delta)=q+2\delta^3$. Prin urmare avem $f(\delta)f(-\delta)=q^2-4\delta^6=q^2+4\frac{p^3}{27}=4\Delta^2$; altfel spus, discriminantul este egal cu a patra parte din produsul valorilor critice.

Dacă $p\lt 0$ atunci $\pm\delta$ sunt reale şi punctele $(\pm\delta,f(\pm\delta))$ sunt "extreme locale" (un maxim şi un minim); dacă acestea sunt separate de către axa $Ox$ - deci dacă $f(\delta)f(-\delta)\lt 0$, adică $\Delta^2\lt 0$ - atunci şi numai atunci, avem trei rădăcini reale distincte. Iar dacă $\Delta^2=0$ (adică fie maximul, fie minimul este situat pe $Ox$), atunci unul dintre punctele critice este rădăcină dublă a ecuaţiei $f(x)=0$ (fiind astfel, uşor de aflat - încât aici, ignorăm cazul $\small \Delta^2=0$).

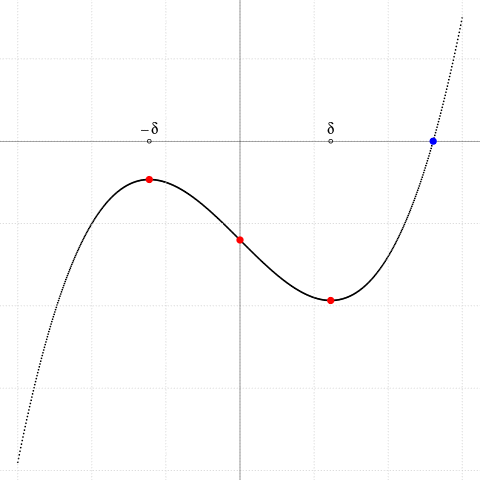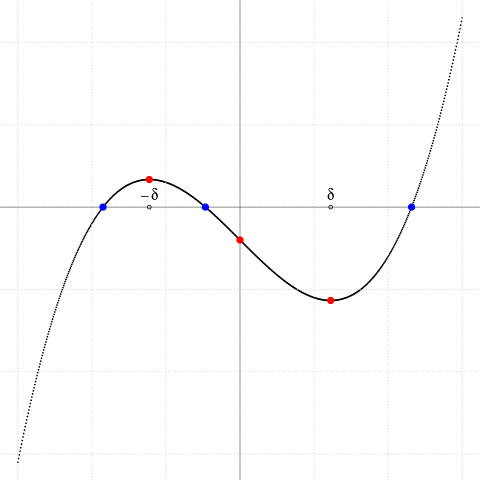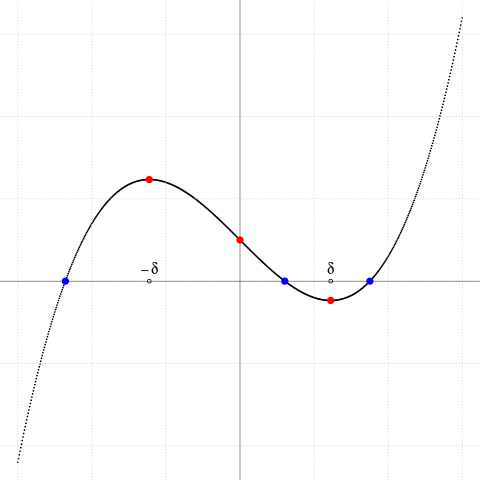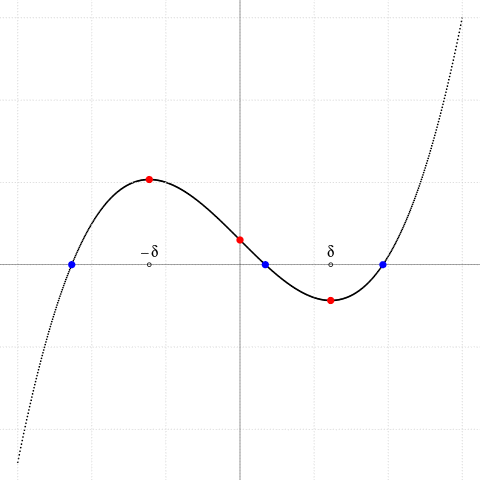
$f(x)=x^3+px+q,$
    $p=-\small 4.5$ ($p\lt 0$: sau una, sau trei rădăcini reale),
    $q=\small -6+0..25*0.5$ (punctul de inflexiune $(0,q)$)

extreme locale $(\pm\delta,f(\pm\delta))$, unde $\small\delta^2=\dfrac{-p}{3}\gt 0$
$f(\delta)f(-\delta)\lt 0\,$ —> 3 rădăcini reale distincte
(şi de fapt, avem: $f(\delta)f(-\delta)=4\Delta^2$)

Avem 3 rădăcini reale distincte (cu $p\lt 0$)
    dacă şi numai dacă $q\in\small\left (\dfrac{2p}{3}\delta,\dfrac{-2p}{3}\delta\right )$

Condiţia ca (1) să aibă trei rădăcini reale distincte se poate formula acum observând că ea este echivalentă cu faptul că ordonata $y=q$ este cuprinsă între maximul şi minimul lui $y=x^3+px$; ori acestea sunt atinse pentru $x=\pm\delta$ şi avem $\delta^3+p\delta=\delta(\delta^2+p)=2p\delta/3$ - de unde avem deocamdată (vom reveni mai jos) concluzia formulată deja în dreapta imaginii.

Programul R prin care am constituit graficul respectiv reflectă o schemă tipică pentru obţinerea unei imagini animate. Întâi introducem funcţia de bază $f(x)=x^3+px$, setăm $p$ şi construim o secvenţă de afixe ale punctelor acesteia (este mai comod de lucrat cu numere complexe!); iniţiem sistemul grafic png() pentru a crea o serie de fişiere ".png", într-un anumit director prestabilit (viitoarele cadre ale animaţiei) - anume, câte unul pentru fiecare valoare $q$ dintr-o anumită secvenţă. Cadrul curent este iniţiat printr-o comandă plot() - care trasează graficul lui $f(x)+q$ - şi este completat apoi prin points() şi text() (marcând punctele importante); în final, închidem sistemul grafic prin dev.off() - astfel, fişierele ".png" construite în memorie sunt salvate pe disc - şi invocăm convert() asupra cadrelor ".png" respective.

cubic <- function(p) function(x) x^3 + p*x
p <- -4.5
f <- cubic(p)
x <- seq(-3, 3, by = 0.01)
z <- x + 1i*f(x)  # afixele unora dintre punctele curbei y = x^3 + px
pcr <- polyroot(c(p, 0, 3))  # rădăcinile ecuaţiei x^3 + p = 0
pucr <- pcr + 1i*f(pcr)  # afixele extremelor lui f(x) = x^3 + px
setwd("1cubics")  # directorul în care se vor salva cadrele create
png(filename = "cubic%02d.png")  # pentru plotare în fişiere ".png"
par(mar=c(0, 0, 0, 0), bty="n")  # anulează marginile ferestrei grafice
for(q in seq(-6, 6, by = 0.5)) {
  # constituie câte un nou cadru (fişier) al animaţiei finale
  plot(z+1i*q, pch=20, cex=0.01, xaxt="n", yaxt="n")  # graficul funcţiei (1)
  grid(); abline(v=0, lwd=0.5); abline(h = 0, lwd=0.5)  # axele Oy, Ox
  cr <- pucr + 1i*q  # punctele critice pentru f(x) = x^3 + px + q
  infl <- mean(cr)  # punctul de inflexiune (mijlocul segmentului extremelor)
  points(c(cr, infl), col="red", pch=19, cex=1.2)
  points(pcr, cex=0.7)  # marchează punctele critice "delta"
  text(sort(pcr), c(expression(-delta), expression(delta)), pos=c(3, 3), cex=1.2)
  roots <- polyroot(c(q, p, 0, 1))  # rădăcinile ecuaţiei x^3 + px +q = 0
  discr <- ifelse(abs(Im(roots)) > 1e-10, NA, "blue")  # arată numai rădăcinile reale
  points(roots, col=discr, pch=19, cex=1.2)
}
dev.off()  # salvează cadrele "*.png", în directorul curent
system("convert -delay 4 -loop 1 *.png cubic3.gif")
#file.remove(list.files(pattern=".png"))  # elimină fişierele "*.png"
setwd("../")  # revine în directorul de lucru iniţial

Precizăm că înainte de a elimina fişierele ".png", am copiat unul dintre ele sub un nume care să-i asigure ultimul loc în secvenţa de cadre şi am relansat convert() direct din linia de comandă - încât să încheiem animaţia într-o poziţie semnificativă pentru cazul a trei rădăcini reale.

Văzând lucrurile în acest fel (angajând derivatele funcţiei şi nu doar calculul algebric), avem imediat unele generalizări. Astfel, pentru ecuaţia $\large x^n+px^m+q=0$ unde $n$ şi $m$ sunt impari şi $n\gt m$: dacă $p\gt 0$, atunci există o singură soluţie reală (fiindcă în acest caz derivata este pozitivă, deci funcţia este strict crescătoare); dacă $p\lt 0$, atunci există sau una singură, sau trei rădăcini reale distincte (fiindcă în acest caz funcţia admite un maxim şi un minim local - care pot fi calculate uşor - iar numărul de rădăcini reale depinde apoi de poziţia extremelor respective faţă de axa Ox).

Desigur… dispunând (ca în programul de mai sus) de o funcţie ca polyroot() - parcă n-am mai avea nevoie de vreo formulă care să exprime rădăcinile. Revenim totuşi la cazul $p\lt 0$, pentru care am obţinut mai sus condiţia de existenţă a trei rădăcini reale distincte $q\in\small\left (\dfrac{2p}{3}\delta,\dfrac{-2p}{3}\delta\right )$; amintindu-ne că $p=-3\delta^2$, putem rescrie această condiţie prin $\left|\dfrac{q}{2\delta^3}\right|\lt 1$ - ceea ce înseamnă că putem găsi $\,\theta\,$ încât $\cos\theta=-\dfrac{q}{2\delta^3}\,\,\small\left(\,=-\dfrac{q}{2\delta^2\delta}=\dfrac{3q}{2p}\sqrt{-\dfrac{3}{p}}\,\right)$.

Amintindu-ne şi formula clasică $4\cos^3\alpha-3\cos\alpha-\cos 3\alpha=0$ (legată de problema celebră a trisecţiunii unghiului) - verificăm direct că pentru $\theta$ considerat mai sus, valoarea $x=2\delta\cos\dfrac{\theta}{3}$ satisface ecuaţia (1): $x^3+px+q=8\delta^3\cos^3\frac{\theta}{3}+2p\delta\cos\frac{\theta}{3}+q=2\delta^3\left(4\cos^3\frac{\theta}{3}+\dfrac{p}{\delta^2}\cos\frac{\theta}{3}+\dfrac{q}{2\delta^3}\right)$ şi acum înlocuind $p=-3\delta^2$ şi $\dfrac{q}{2\delta^3}=-\cos\theta$ obţinem într-adevăr, $0\,$ - conform formulei trisecţiunii scrise mai sus, pentru $\alpha=\theta/3$   (F. Viète este cel care - pe la 1600 - a legat rezolvarea ecuaţiei cubice în cazul existenţei a trei rădăcini reale distincte, de trisecţia unghiului).

Încât în final, cele trei rădăcini reale distincte - cazul $\small p\lt 0$ şi $\small\left|\dfrac{q}{2\delta^3}\right|\lt 1$, unde $\small\delta=\sqrt{-p/3}$ - sunt:

$2\sqrt{\dfrac{-p}{3}}\cos\,\dfrac{\theta+2k\pi}{3},\,\,\small k=0,1,2$ unde $\theta=\arccos\,\dfrac{3\sqrt{3}\,q}{2p\sqrt{-p}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,(3)$

Următorul mic experiment permite verificarea numerică a formulelor la care am ajuns (folosind stopifnot() pentru a exclude $p$ şi $\theta$ care nu satisfac condiţiile necesare):

test3r <- function(p, q) {  # modelează formulele celor 3 rădăcini reale
  stopifnot(p < 0)  # pentru p > 0, nu este definit sqrt(-3/p)
  teta <- 1.5*sqrt(-3/p) * q/p;  
  stopifnot(abs(teta) < 1)  # altfel nu este definit acos(teta)
  teta <- acos(teta)
  2*sqrt(-p/3)*cos((teta + 2*(0:2)*pi)/3)  # returnează rădăcinile calculate
}
print(test3r(-7, 6))  # x^3 - 7x + 6 = 0
roots <- runif(2, min=-100, max=100)  # două rădăcini oarecare (generate aleatoriu)
print(roots)
roots[3] <- -sum(roots)  # a treia este opusa sumei celorlalte două
p <- roots[1]*roots[2] + roots[1]*roots[3] + roots[2]*roots[3]
q <- -roots[1]*roots[2]*roots[3]  # p şi q rezultă din relaţiile lui Viète
print(test3r(p, q))

> source("test3.R")  # lansează programul de mai sus (constituit în fişierul "test3.R")
[1]  2 -3  1  # rădăcinile ecuaţiei x^3 - 7x + 6 = 0
[1] -30.47814 -32.60658  # cele două rădăcini generate aleatoriu
[1]  63.08471 -32.60658 -30.47814  # rădăcinile calculate de test3()

Putem evidenţia acum şi legătura celor trei soluţii reale cu numerele complexe (care a fost anticipată de pe vremea lui Cardano, sub denumirea de casus irreductibilis). Soluţiile (3) sunt (evident) părţile reale ale punctelor de afixe $2\delta\left(\cos\frac{\theta+2k\pi}{3}+i\sin\frac{\theta+2k\pi}{3}\right),\,\small k=0..2$ şi putem recunoaşte imediat că aceste puncte se obţin rotind cu unghiul $\theta/3$ şi scalând cu factorul $2\delta$, rădăcinile de ordinul 3 ale unităţii:

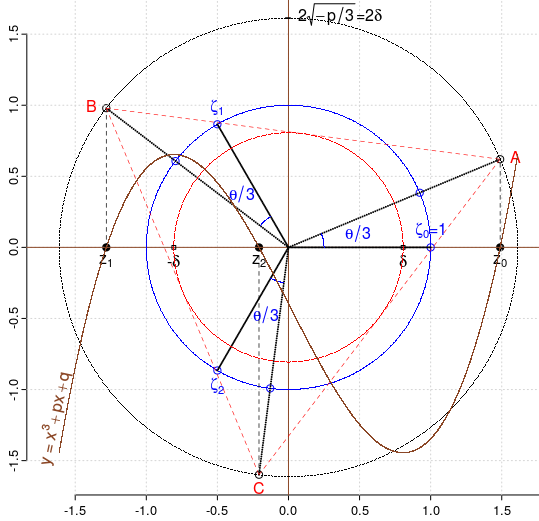
roteşte $\zeta_i,\,\small i=0..2$ (rădăcinile de ordinul 3 ale unităţii) cu unghiul $\theta/3$;

proiectează (din origine) imaginile rezultate, pe cercul de rază $2\delta$ (unde $\pm\delta$ sunt rădăcinile derivatei), obţinând punctele A, B, C;

abscisele punctelor A, B, C sunt rădăcinile $z_i,\,\small i=0..2$ ale ecuaţiei $x^3+px+q=0$, cu $\small p\lt 0,\,\,\left|\,0.5\,q/\delta^3\,\right|\lt 1,\,\theta=\arccos\small\left(1.5\,q\,/\,(p\,\delta)\right)$

Triunghiul ABC este echilateral; cercul înscris lui conţine punctele critice $(\pm\delta, 0)$.

Construcţia tocmai descrisă conduce "invers", la această exprimare: dacă $x^3+px+q=0$ are trei rădăcini reale distincte, atunci proiecţiile verticale (într-un acelaşi sens) ale acestora pe cercul de rază $\small2\sqrt{-p/3}$ (dublul valorii absolute a punctelor critice) centrat în origine, sunt vârfurile unui triunghi echilateral (iar cercul înscris acestuia trece prin punctele critice; într-adevăr: în orice triunghi avem R ≥ 2r, cu egalitate numai pentru triunghi echilateral; în cazul nostru R fiind $2\delta$, avem r=$\delta$ - astfel că cercul înscris triunghiului ABC conţine punctele $\small(\pm \delta, 0)$).

Am evidenţiat mai sus că în R "este mai comod de lucrat" cu afixele punctelor (decât cu abscise şi ordonate); iar în cursul experimentelor şi verificărilor numerice "ne-am lovit" şi aici de conversia tacită a valorilor de diverse tipuri dintr-un acelaşi vector, la tipul cel mai general ("real" devenind automat "complex"), precum şi de faptul că funcţiile matematice au implementări "generice" (fiind utilizată în mod tacit, versiunea potrivită tipului argumentului):

> acos(2)  # 2 este în mod implicit de tip "numeric" (număr real)
[1] NaN  # Cu x real, acos(x) este definită numai pentru x ∈ [-1, 1] 
> acos(c(2, 0i))  # 2 este convertit automat la clasa "complex"
[1] 0.000000+1.316958i 1.570796+0.000000i  # recunoaştem acos(0) = π/2 ≈ 1.570796
> cos(1.316958i)
[1] 2+0i  # deci acos(as.complex(2)) = 1.316958i

Acest mic experiment pe seama funcţiei acos(), sugerează următoarele: dacă $p$ şi $q$ sunt numere reale, atunci într-adevăr - formula (3) este valabilă numai dacă valoarea $\left|0.5\,q/\delta^3\right|$ nu depăşeşte 1 (numai astfel, i se poate aplica funcţia reală "arccos()"); dar dacă am vedea $p$ şi $q$ ca numere complexe (sau le-am avea date aşa), atunci formula (3) ar fi valabilă totdeauna (fiindcă funcţia complexă "arccos()" este definită "peste tot").
Înseamnă că putem rezolva (cel puţin… lucrând în R) oricare ecuaţie cubică (indiferent de caz) folosind doar formula (3) (şi nu formule diferite, depinzând de numărul de rădăcini reale) - cu singura condiţie ca $p$ şi $q$ să fie de tip "complex":

solve_cubic <- function(p, q) {  # p ≠ 0 (evită împărţirea cu 0)
  p <- as.complex(p); q <- as.complex(q)
  delta <- sqrt(-p/3)
  cos_t <- -0.5*q/delta^3
  teta <- tryCatch(
    acos(cos_t) / 3,
    warning = function(e) {  # când calculul acos() "eşuează" (returnează 'NA')
      # print(e)  # NaNs produced in function "acos"
      # print(c(Re(p),Re(q)))  
      return(NA)
    }
  )
  2*delta*cos(teta + 2*(0:2)*pi/3)  # returnează cele 3 rădăcini (dacă teta != NA)
}

Am dat peste cazuri (de argument "complex") în care acos() produce un mesaj de "atenţionare" (dar încă nu ştiu precis, motivul) - de aceea am folosit aici tryCatch(): dacă acos() eşuează, atunci returnăm valoarea generală standard "NA" (şi eventual, afişăm coeficienţii); altfel, se calculează $\small\theta/3$ şi se returnează vectorul valorilor calculate prin formula (3).

Pentru a atesta că valorile returnate de solve_cubic() sunt într-adevăr, rădăcinile ecuaţiei - putem proceda în mai multe moduri (cel mai banal fiind verificarea directă); alegem aici să confruntăm valorile respective cu rădăcinile furnizate prin polyroot() şi testăm pentru o gamă de coeficienţi suficient de "largă" (încât să avem toate cazurile: o singură rădăcină reală, trei rădăcini reale, respectiv - rădăcini complexe nereale):

dom <- seq(-2, 2, by=0.01)  # dom <- (-10:10)
for(p in dom[dom != 0]) {
  for(q in dom) {
    root1 <- sort(polyroot(c(q, p, 0, 1)))  # x^3 + px + q = 0
    root2 <- sort(solve_cubic(p, q))  # aplică formula (3)
    ifelse(abs(root1) - abs(root2) > 1e-7, {  # 1E-10 este totuşi prea mic
           print(c(Re(p), Re(q)))
           print(root1); print(root2)
    }, NA)
  }
}

Prin această secvenţă se rezolvă un număr de 400×401=160400 ecuaţii (având $p\ne 0$ şi $q$ între $-2$ şi $2$ - din sutime în sutime). Pentru a confrunta răspunsurile din polyroot() şi respectiv solve_cubic(), am ordonat vectorii respectivi (folosind sort(), care pentru "complex" ordonează lexicografic - după partea reală şi apoi, după partea imaginară) şi am testat dacă diferenţa modulelor componentelor de acelaşi rang depăşeşte cumva $\small 10^{-7}$ (caz în care afişăm vectorii respectivi, însemnând că în acel caz formula (3) nu dă totuşi rădăcinile dorite); precizăm însă că micşorarea erorii de comparare la $\small 10^{-10}$ atrăgea afişarea tuturor vectorilor - dar componentele de acelaşi rang diferă numai după a opta sau a noua zecimală (deci pot fi considerate "egale").

Execuţia secvenţei de comenzi de mai sus se încheie "curat" (nu se afişează nimic), deci avem o confirmare suficientă a aserţiunii făcute mai sus (formula (3) rezolvă orice ecuaţie cubică). Desigur, era bine să fi contorizat cumva, cazurile în care acos() nu a putut fi operată; în acest scop, putem prevedea o variabilă globală iniţializată cu $0$ (în exteriorul funcţiei solve_cubic()) şi incrementată în secţiunea "warning" din corpul comenzii tryCache(); am obţinut astfel, că acos() a eşuat într-un număr de (numai) 2002 ecuaţii (în contextul specificat mai sus).

Motivul cel mai obişnuit pentru care un calcul numeric "eşuează" ţine de modul în care este controlată acumularea erorilor de rotunjire inerente. Să vedem cum se petrec lucrurile…

Mai întâi, să definim în exteriorul funcţiei solve_cubic() o matrice cu 2002 linii (sau câte ar fi necesare înregistrării coeficienţilor ecuaţiilor la care calculul eşuează) şi două coloane:

nw <- 1
pq <- matrix(nrow=2002, ncol=2, byrow=TRUE)

şi să modificăm în solve_cubic() secţiunea "warning" din comanda tryCatch() astfel:

  teta <- tryCatch(
    acos(cos_t) / 3,
    warning = function(e) {
      pq[nw, ] <<- c(Re(p), Re(q)); nw <<- nw + 1
      return(NA)
    }
  )

Reluând acum secvenţa prin care am rezolvat cele 160400 ecuaţii, obţinem în matricea "pq" coeficienţii fiecăreia dintre cele 2002 ecuaţii la care calculul acos() a eşuat:

> head(pq, 3)
      [,1]  [,2]
[1,] -1.43 -2.00  # p = -1.43, q = -2 
[2,] -1.43  2.00
[3,] -1.42 -1.98

> tail(pq, 3)
         [,1] [,2]
[2000,] -0.06 0.36
[2001,] -0.04 0.01
[2002,] -0.03 0.03  # p = -0.03, q = 0.03

Pentru a asigura o anumită generalitate concluziilor, selectăm aleatoriu (prin sample()) una dintre aceste 2002 linii; apoi, investigăm cazul respectiv - anume, determinăm valoarea "cos_t" ca în solve_cubic(), o afişăm cu un număr cât mai mare de zecimale şi ne convingem că într-adevăr, pentru valoarea respectivă acos() eşuează:

test_acos <- function() {
  eq <- pq[sample(1:2002, 1), ];  print(eq)
  p <- as.complex(eq[1]);  q <- as.complex(eq[2])
  delta <- sqrt(-p/3);  cos_t <- -0.5*q/delta^3
  cat(paste0("cos_t = ", format(cos_t, nsmall=20), "\n"))
  acos(cos_t)
}

> test_acos()
[1] -0.70 -1.69
cos_t = 7.49706939828371954349+0i
[1] NaN+2.703181i  # calculul părţii reale pentru acos(cos_t) eşuează 
Warning message:
In acos(cos_t) : NaNs produced in function "acos"

Poate că nu vom reuşi să lămurim complet "de ce" - dar acum este simplu să verificăm dacă nu cumva, calculul eşuează din "vina" implementării existente în R pentru funcţia complexă acos(); copiem valoarea "cos_t" tocmai afişată, deschidem într-un nou terminal o consolă de python şi încercăm funcţia cmath.acos() pe valoarea respectivă:

vb@Home:~/4_art/Complex$ python
Python 2.7.12 (default, Nov 19 2016, 06:48:10) 
[GCC 5.4.0 20160609] on linux2
Type "help", "copyright", "credits" or "license" for more information.
>>> from cmath import acos
>>> cos_t = 7.49706939828371954349
>>> acos(cos_t)
-2.703181485277956j

Revenind în consola R, putem proba că aplicând cos() valorii acos(cos_t) obţinute în consola python - reobţinem aproximativ, valoarea iniţială "cos_t":

> print(cos(-2.703181485277956i), digits=20)
[1] 7.4970693982837204317+0i  # coincide până la a 13-a zecimală cu valoarea "cos_t"

Repetând test_acos() de câteva ori (şi procedând ca mai sus) am constatat de fiecare dată că cmath.acos() din python "merge" fără probleme (în timp ce acos() din R eşuează, pentru cazurile respective). Deci "de vină" pentru eşecul rezolvării prin solve_cubic() în cazul celor 2002 ecuaţii evidenţiate mai sus este o anumită deficienţă de implementare în R a funcţiei acos(); altfel, sub condiţia unei implementări "corecte" a funcţiilor de variabilă complexă, formula (3) modelată de solve_cubic() (pe care am reformula-o acum în python) rezolvă unitar oricare ecuaţie cubică.

Desigur, "oricare ecuaţie" include şi cazul când coeficienţii sunt numere complexe oarecare. Să testăm rezolvarea prin formula (3) - deci folosind solve_cubic() (în care "curăţăm" secţiunea din "warning" inserată mai sus) - a unei astfel de ecuaţii.

Considerăm trei numere complexe $z_i$, calculăm coeficienţii polinomului $\Pi (x-z_i)$ care le are ca rădăcini, îl reducem la forma (1), rezolvăm prin solve_cubic() ecuaţia redusă şi translatăm înnapoi rădăcinile găsite astfel:

test_cubic <- function(z1, z2, z3) {  # trei numere complexe oarecare
  a <- -(z1 + z2 + z3)
  b <- z1*z2 + z1*z3 + z2*z3
  c <- -z1*z2*z3  # x^3 + ax^2 + bx + c = 0 are rădăcinile z1, z2, z3
  cat("\t\tx^3 + ax^2 + bx + c:  ", c(1, a, b, c), "\n")
  p <- (3*b - a^2) / 3 
  q <- (2*a^3 - 9*a*b + 27*c) / 27  # ecuaţia redusă x^3 + px + q = 0
  cat("\t\tx^3 + px + q:  ", c(1, p, q), "\n")
  solve_cubic(p, q) - a/3  # rădăcinile ecuaţiei reduse sunt (z_i + a/3)
}

Invocăm funcţia de mai sus pentru o listă conţinând rădăcinile câtorva ecuaţii:

for(z in list(c(2-3i, 1+2i, 5-4i), c(1, 2, 3), c(1i, 2, 3))) {
  cat("test_cubic(", z, "):\n")
  cat("\trădăcinile găsite prin (3): ", test_cubic(z[1], z[2], z[3]), "\n\n")
}

> source("cubic1.R")  # fişierul care cuprinde cele două secvenţe de mai sus
test_cubic( 2-3i 1+2i 5-4i ):
		x^3 + ax^2 + bx + c:   1+0i -8+5i 19-16i -44+27i 
		x^3 + px + q:   1+0i 6+10.66667i -13.48148+14.51852i 
	rădăcinile găsite prin (3):  5-4i 1+2i 2-3i 
test_cubic( 1 2 3 ):
		x^3 + ax^2 + bx + c:   1 -6 11 -6 
		x^3 + px + q:   1 -1 0 
	rădăcinile găsite prin (3):  3+0i 1+0i 2+0i 
test_cubic( 0+1i 2+0i 3+0i ):
		x^3 + ax^2 + bx + c:   1+0i -5-1i 6+5i 0-6i 
		x^3 + px + q:   1+0i -2+1.666667i 0.185185-1.148148i 
	rădăcinile găsite prin (3):  3+0i 0+1i 2+0i 

Pentru acest caz - când (1) are coeficienţi complecşi - ar fi de lămurit mai departe, cum sunt poziţionate în plan rădăcinile şi punctele critice.