Rădăcinile ecuaţiei $f(z)=z^3+pz+q=0,\,p,q\in\mathbb{C}^*$ pot fi exprimate sub forma:

$\large z_k=2\delta\cos\left(\theta+\frac{2k\pi}{3}\right),\,\normalsize k=0..2\hskip5em (1)$

unde $\delta=\sqrt{-p/3}\,$ iar $\theta=\arccos\left(-q/(2\delta^3)\right)\,/\,3$ (fără condiţiile obişnuite, pentru valorile argumentelor funcţiilor!).

Pentru coeficienţi reali $p, q$ astfel încât $p\lt 0$ şi $\left|\,q/(2\delta^3)\,\right|\lt 1$ (când avem trei rădăcini reale distincte), formula (1) a fost stabilită de F. Viète, iar satisfacţia - când chiar şi numerele negative, încă erau vizate cu suspiciune - consta în obţinerea unei formule "curate" pentru rădăcini (faţă de formula algebrică a lui Cardano, în care apărea în mod inevitabil entitatea străină "$\small\sqrt{-1}$"); pentru acest caz am evidenţiat în [1] că $z_k$ sunt proiecţiile pe axa reală ale punctelor obţinute prin rotirea cu unghiul $\theta$ a rădăcinilor de ordinul trei ale unităţii, urmată de scalarea cu factorul $2\delta$.

Dar am observat în [1] (verificând şi printr-un program R) că formula (1) este valabilă în toate cazurile (indiferent de natura rădăcinilor) - dacă se consideră coeficienţii ca numere complexe, iar radical, cosinus şi arccosinus sunt angajate ca funcţii de variabilă complexă.

Euler a introdus notaţia $i=\sqrt{-1}$ (precum şi "$e$" pentru baza "logaritmului natural") şi pe la 1750, a stabilit - comparând dezvoltările în serie de puteri - că funcţiile trigonometrice şi exponenţiala (de variabilă reală) sunt legate prin formula $\cos x+i\sin x=e^{ix}$; dacă înlocuim aici variabila reală $x$ cu variabila complexă $z$, am avea $e^{iz} =\cos z+i\sin z$ - de unde am găsi definiţia $\cos z=\left(e^{iz}+e^{-iz}\right)/\,2,\,z\in\mathbb{C}$, prin care (1) devine:

$\large z_k=\delta e^{i\theta}e^{\frac{2k\pi}{3}i}+\delta e^{-i\theta}e^{-\frac{2k\pi}{3}i}\;\;\;\normalsize (k=0..2;\,\theta\in\mathbb{C}) \hskip5em (2)$

Dacă $\theta$ ar fi număr real, atunci (dar numai în acest caz) am avea $e^{-i\theta}=\overline{e^{i\theta}}$ şi - fiindcă suma a două numere complexe conjugate este număr real - am regăsi exact formula dată de Viète (1). Dar aici vizăm situaţia în care $\small f(z)$ are rădăcini distincte şi cu partea imaginară nenulă (încât $\theta\in\mathbb{C}$); în plus, considerăm numai cazul când punctele $z_k$ nu sunt coliniare.

În cele trei relaţii (2), $\delta e^{i\theta}=a$ şi $\delta e^{-i\theta}=b$ sunt "constante" (nu depind de punctul $z_k,\,k=0..2$) - astfel că vom putea folosi rezultatul următor:

Lemă Pentru orice două puncte date $a, b\in\mathbb{C^*}$, locul punctelor $z=ae^{it}+be^{-it},\, t\in (-\pi, \pi]$ este elipsa ale cărei focare au afixele $\pm 2\sqrt{ab}$ (şi "semiaxa mare" este egală cu $|a|+|b|$).

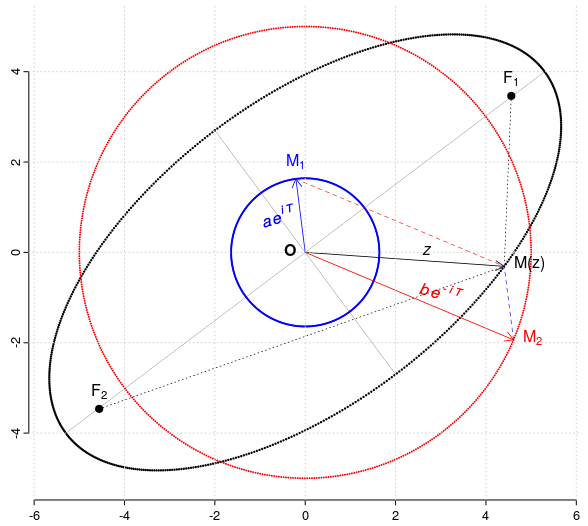
M₁ (cu afixul $ae^{it}$) şi M₂ (cu afixul $be^{-it}$) parcurg cercurile cu centrul O şi razele $|a|$ şi respectiv $|b|$, cu aceeaşi "viteză unghiulară" dar în sensuri contrare; atunci punctul M, al cărui vector de poziţie însumează vectorii de poziţie ai punctelor M₁ şi M₂ - având astfel afixul $z=ae^{it}+be^{-it}$ - parcurge o elipsă cu centrul O şi focarele F₁ şi F₂ (şi OF₁ este bisectoarea unghiului M₁OM₂).

Verificăm mai jos proprietatea definitorie pentru o elipsă: suma distanţelor lui M la focarele indicate este constantă.

Avem MF₁ = $|z-2\sqrt{ab}|=|ae^{it}+be^{-it}-2\sqrt{ab}|=\left|\left(\sqrt{a}\,e^{it/2}-\sqrt{b}\,e^{-it/2}\right)^2\right|=|u-v|^2$; obţinem astfel, MF₁ + MF₂=$|u-v|^2+|u+v|^2=2|u|^2+2|v|^2=2(|a|+|b|)$ (= constant). Acest calcul este cam "mecanic": avem într-adevăr, $ab=ae^{it}be^{-it}=(\sqrt{a}e^{it/2})^2(\sqrt{b}e^{-it/2})^2$ (şi $=(uv)^2$), dar avem $\sqrt{ab}=\sqrt{a}\,\sqrt{b}$ numai dacă $-\pi\lt \arg{a}+\arg{b}\le\pi$ - ceea înseamnă că ar mai fi de analizat nişte cazuri, pentru a sfârşi demonstraţia (dar aici, le vom ignora).

Cu Lema redată mai sus, deducem că punctele $z_k$ date de (2) (şi presupuse necoliniare) sunt situate pe elipsa de focare $\pm 2\sqrt{ab}=\pm 2\sqrt{(\delta e^{i\theta})(\delta e^{-i\theta})}=\pm 2\sqrt{\delta^2}=\pm 2\delta$; panta axei mari este $\tan(\arg \delta)$ - dar atenţie: vârfurile elipsei nu rezultă punând $t=\arg(\delta)$ în ecuaţia elipsei $z=ae^{it}+be^{-it}$, fiindcă argumentul lui $z$ nu este $t$!

Centrul O(0, 0) al elipsei este centrul de greutate al triunghiului rădăcinilor (fiindcă suma acestora este 0); iar ştiind centrul, un focar şi un punct al ei, elipsa este unic determinată. Am regăsit în fond, o teoremă a lui Steiner: există o singură elipsă circumscrisă unui triunghi şi având centrul în centrul de greutate al acestuia. Această teoremă are şi o a doua parte: există o singură elipsă înscrisă unui triunghi, tangentă laturilor în mijloacele acestora, cu centrul în centrul de greutate; ea este transformata elipsei lui Steiner prin omotetia de centru O şi raport 1/2 - adică în cazul nostru, are ecuaţia $z=0.5(ae^{it}+be^{-it}),\, t\in (-\pi, \pi]$, iar focarele au afixele $\,\pm\delta$.

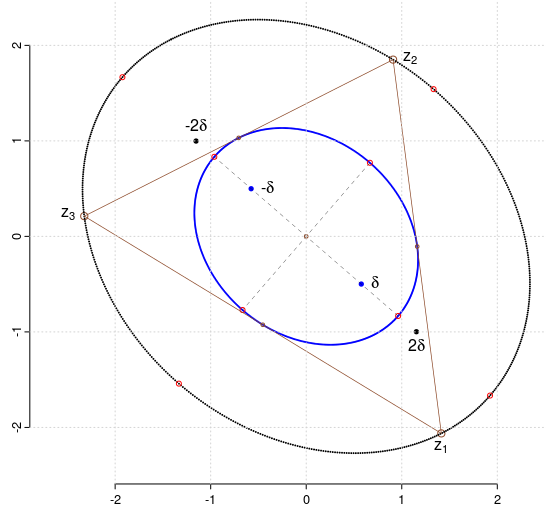
$z_1,z_2,z_3$ reprezintă rădăcinile complexe (dar necoliniare) ale unui polinom redus de gradul trei (cu coeficienţi complecşi), iar $\pm\delta$ sunt rădăcinile derivatei acestuia (polinomul fiind "redus", originea este zeroul derivatei a doua şi totodată este centrul de greutate al rădăcinilor).

Atunci, elipsele lui Steiner (circumscrisă şi respectiv, înscrisă) corespunzătoare triunghiului rădăcinilor au focarele în punctele de afixe $\pm 2\delta$ şi respectiv $\pm\delta$; axa mare are panta egală cu $\tan(\arg(\delta))$.

Pentru reprezentarea grafică, am generat aleatoriu trei numere complexe, am determinat coeficienţii $p$ şi $q$ ai ecuaţiei reduse care le are ca rădăcini şi apoi am plotat elipsele (marcând focarele, vârfurile şi punctele de tangenţă cu laturile triunghiului) folosind ecuaţiile constituite mai sus (iar altfel, prin comenzi R precum cele specificate deja în [1]); figura de deasupra corespunde cazului numeric următor:

> source("cubic4.R")
z^3 + pz + q   1+0i  -0.250198+1.726293i  12.01112+0.64329i 
delta =  0.5765599-0.499021i   Arg(delta) = -0.7134324 
panta axei mari: tan(Arg(delta)) = tan(-0.7134324) = -0.8655146 
theta =  0.316358+1.100355i 
z1, z2, z3   1.414142-2.06243i  0.909091+1.850613i  -2.323232+0.211817i 
vârfurile elipsei înscrise: 
    ±(0.9624316-0.83268i) cu Argumentul =  -0.7132431  # ≈ Arg(delta)
    ±(0.6662058+0.7709458i) cu Argumentul =  0.8581498 

Fiind complicat de exprimat afixele vârfurilor elipsei, am imaginat funcţia următoare - prin care se parcurge elipsa cu un anumit pas (care ar fi "uniform" în cazul cercului), returnând acel punct al cărui argument este acceptabil de apropiat de unghiul corespunzător pantei axei:

find_vf <- function(angle = Arg(delta)) {  # pentru a doua axă: pi/2 + Arg(delta)
  c1 <- 0.5*delta*exp(1i*teta)  # pentru punctele M1
  c2 <- 0.5*delta*exp(-1i*teta)  # pentru punctele M2
  t <- seq(-pi, pi, length=4000)  # 'length' abscise "echidistante" pe [-π, π] 
  z <- c1*exp(1i*t) + c2*exp(-1i*t)  # punctele M ale elipsei Steiner înscrise
  err <- 1.e-3  # eroarea considerată pentru compararea valorilor 
  for(i in 1:4000) {  # caută punctul elipsei de argument ≈ 'angle'
    if(abs(Arg(z[i]) - angle) < err)
      return(z[i])  # un vârf al elipsei; cel opus va fi -z[i]
  }
  print("error")  # eroarea de comparare este totuşi, prea mică
}

Se vede în exemplul numeric prezentat mai sus că argumentul punctului găsit prin funcţia de mai sus diferă de cel "exact" care este $\arg(\delta)$, cu mai puţin de două zecimi de miime (ceea ce este foarte mulţumitor, pentru reprezentările grafice).

Teoretic, ceea ce am evidenţiat mai sus (plecând însă de la formula trigonometrică a rădăcinilor, dată de Viète) constituie teorema lui Marden: punctele critice ale unui polinom de gradul trei, cu rădăcini complexe şi necoliniare, sunt focarele elipsei Steiner înscrise triunghiului rădăcinilor (unica elipsă centrată în baricentru şi tangentă laturilor în mijloace).